人教版2下数学 3.4《轴对称的剪纸问题》同步练习(含答案)
文档属性
| 名称 | 人教版2下数学 3.4《轴对称的剪纸问题》同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 450.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 11:06:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.4《轴对称的剪纸问题》同步练习
班级:_________ 姓名:__________
一、选择题
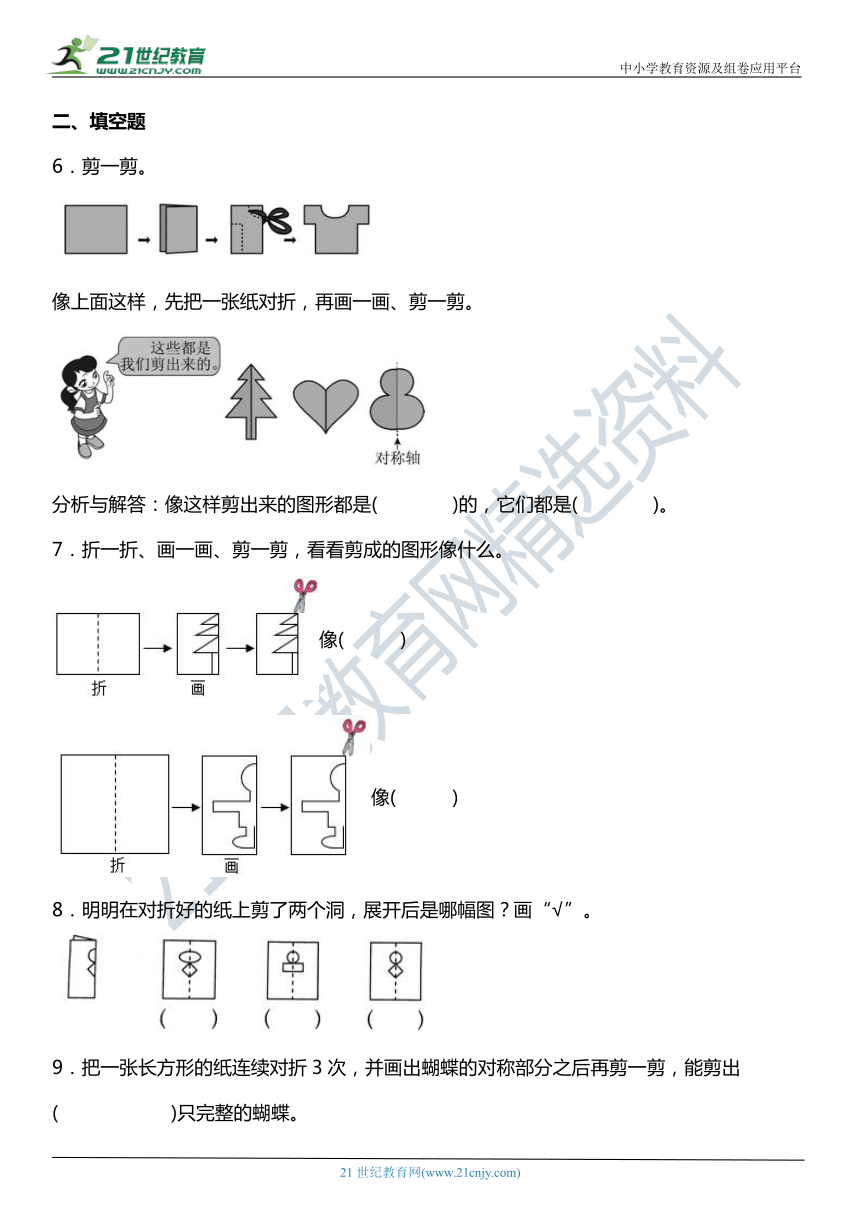
1.下面图案( )是从上面剪下来的。
A. B. C.
2.是从对折的( )上剪下来的。
A. B. C.
3.将空白部分剪掉,余下的部分是( )。
A. B. C.
4.按下图的顺序操作,剪下并展开后得到的图形是( )号。
A. B. C. D.
5.按来剪,剪出( )图形;按来剪,剪出( )图形。
① ② ③
A.①② B.①③ C.③②
二、填空题
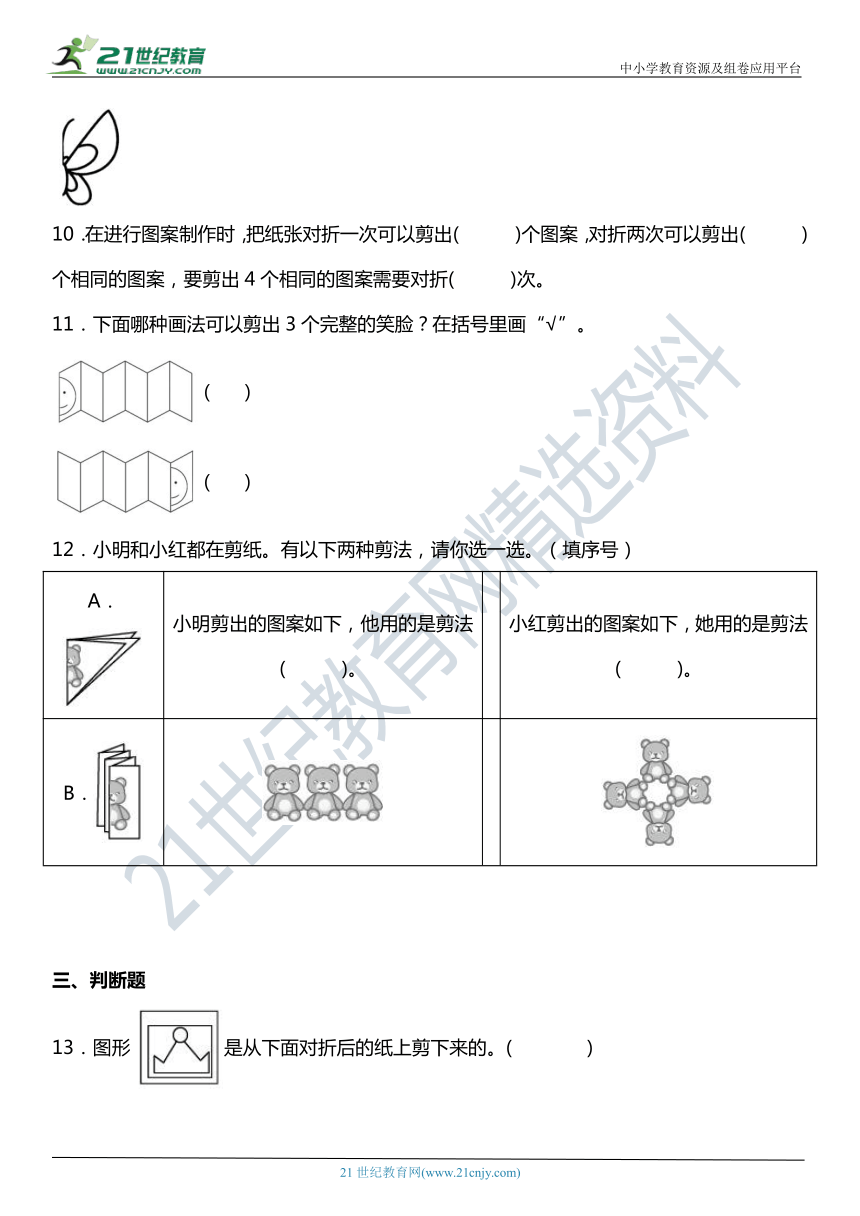
6.剪一剪。
像上面这样,先把一张纸对折,再画一画、剪一剪。
分析与解答:像这样剪出来的图形都是( )的,它们都是( )。
7.折一折、画一画、剪一剪,看看剪成的图形像什么。
像( )
像( )
8.明明在对折好的纸上剪了两个洞,展开后是哪幅图?画“√”。
9.把一张长方形的纸连续对折3次,并画出蝴蝶的对称部分之后再剪一剪,能剪出( )只完整的蝴蝶。
10.在进行图案制作时,把纸张对折一次可以剪出( )个图案,对折两次可以剪出( )个相同的图案,要剪出4个相同的图案需要对折( )次。
11.下面哪种画法可以剪出3个完整的笑脸?在括号里画“√”。
( )
( )
12.小明和小红都在剪纸。有以下两种剪法,请你选一选。(填序号)
A. 小明剪出的图案如下,他用的是剪法( )。 小红剪出的图案如下,她用的是剪法( )。
B.
三、判断题
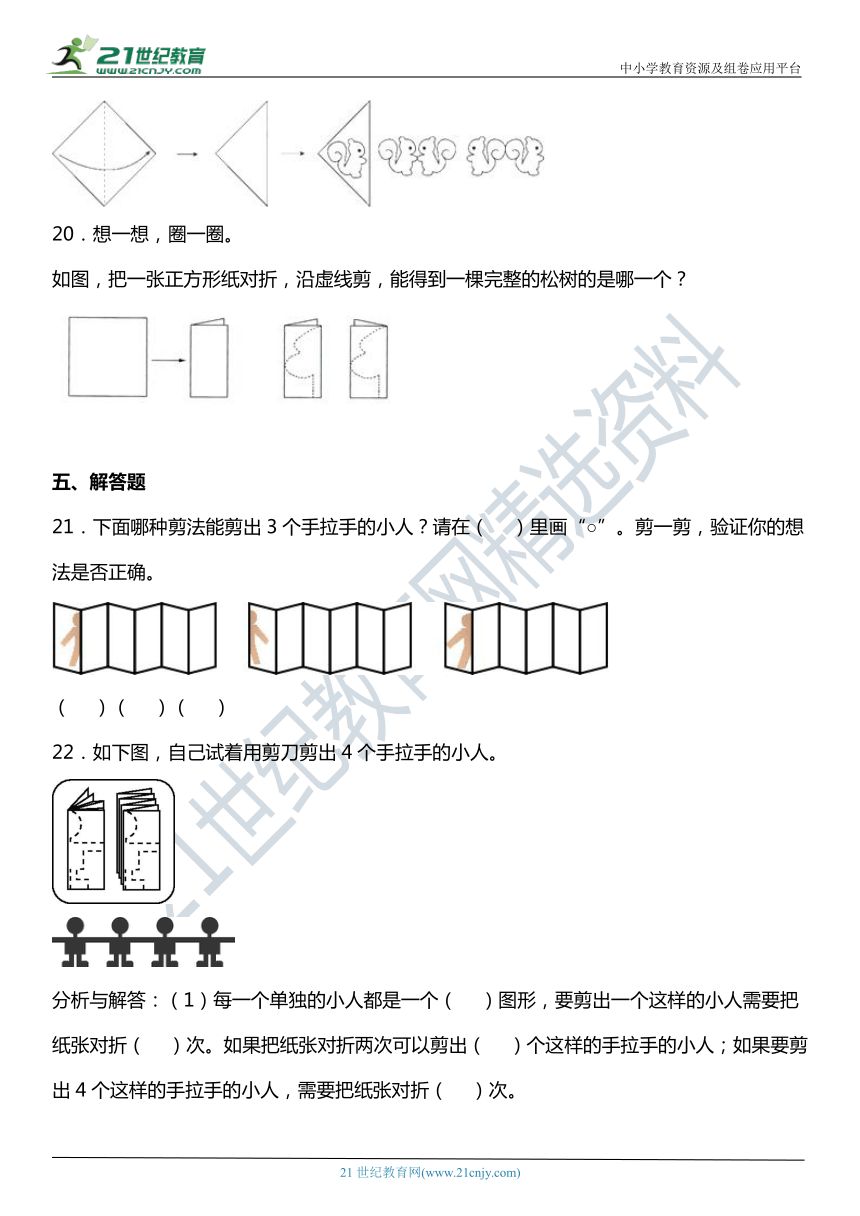
13.图形是从下面对折后的纸上剪下来的。( )
14.是从对折剪下来的。( )
15.是从下面对折的纸上剪下来的。( )
16.剪两个手拉手小纸人要对折1次。( )
17.从左图中可以剪出。( )
四、作图题
18.想一想,圈一圈。
(1)如图,把一张正方形纸对折,沿虚线剪,能得到一棵完整的松树的是哪一个?
(2)要想得到六边形,下列哪种剪法是正确的?
19.按照下面的方式折、画、剪(并描出眼睛),得到的是哪幅图?请圈一圈。
20.想一想,圈一圈。
如图,把一张正方形纸对折,沿虚线剪,能得到一棵完整的松树的是哪一个?
五、解答题
21.下面哪种剪法能剪出3个手拉手的小人?请在( )里画“○”。剪一剪,验证你的想法是否正确。
( )( )( )
22.如下图,自己试着用剪刀剪出4个手拉手的小人。
分析与解答:(1)每一个单独的小人都是一个( )图形,要剪出一个这样的小人需要把纸张对折( )次。如果把纸张对折两次可以剪出( )个这样的手拉手的小人;如果要剪出4个这样的手拉手的小人,需要把纸张对折( )次。
你有几种折纸的方法?自己试着折一折,并剪一剪。
参考答案:
1.B
【分析】找到剪下来的图案与原长方形空白的图案相吻合的,就是从原长方形上面剪下来的。
【详解】由题意分析得:
图案是从上面剪下来的。
故答案为:B
2.B
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】是从对折的上剪下来的;
故答案为:B
【点睛】此题考查了轴对称的意义及在实际当中的运用。
3.A
【分析】依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,据此即可进行解答。
【详解】将空白部分剪掉,余下的部分是。
故答案为:A
【点睛】此题主要考查轴对称图形的意义及认识。
4.A
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】由图分析,剪开后的图形应为对称图形且沿对折线对称,由于排除B、D在观察海豚的嘴离对折线很近,则展开后的图上左右两边海豚嘴也应很近,所以排除C,故选A。
【点睛】此题考查了轴对称的意义及在实际当中的运用。
5.C
【分析】轴对称图形是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴,据此解答。
【详解】按 来剪,剪出()图形;按来剪,剪出( )图形。
故答案为:C
【点睛】本题主要考查了根据轴对称图形剪纸的应用。
6. 对称 轴对称图形
【分析】如果沿某条直线对折,对折的两部分是完全重合的,这样的图形为轴对称图形。这条直线叫做这个图形的对称轴。
【详解】像题干中这样剪出来的图形都是对称的,它们都是轴对称图形。
【点睛】熟练掌握轴对称图形的定义是解题关键。
7. 树 人
【解析】略
8.
【详解】略
9.4
【分析】对折3次能把纸分成2×2×2=4×2=8份,每2份剪出1只完整蝴蝶,所以共剪出8÷2=4只完整的蝴蝶。
【详解】根据分析可知:把一张长方形的纸连续对折3次,并画出蝴蝶的对称部分之后再剪一剪,能剪出(4)只完整的蝴蝶。
【点睛】题中利用了轴对称只画了半只蝴蝶,因此要把分成的份数除以2。
10. 1 2 3
【分析】对折一次是把纸分成两份,每一份是半个图案,所以能剪出一个图案,以此类推,对折2次就是把纸分成了4份,也就是可以剪出2个相同的图案,对折3次就是把纸给分成了8份,可以剪出4个相同的图案。
【详解】在进行图案制作时,把纸张对折一次可以剪出(1)个图案,对折两次可以剪出(2)个相同的图案,要剪出4个相同的图案需要对折(3)次。
【点睛】本题主要考查学生对轴对称图形的认识和对“对折”概念的理解。解决此题时如果不理解,也可以具体操作一下。
11.( )(√)
【解析】略
12. B A
【解析】略
13.×
【详解】略
14.√
【详解】略
15.×
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可。
【详解】
如图所示,是从这样对折的纸上剪下来的。
故答案为:×
【点睛】解答此题的依据是:轴对称图形的概念及特征。
。
16.×
【分析】要想剪出两个手拉手小纸人,应将纸对折2次,把这张纸平均分成4份,在对折好的纸上剪出一半的小纸人,则4个一半的小纸人可以组成两个手拉手小纸人。据此判断。
【详解】剪两个手拉手小纸人要对折2次。说法错误。
故答案为:×
【点睛】本题考查轴对称的剪纸问题,应亲自动手剪一剪,即可得出结论。
17.√
【分析】依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,据此即可进行解答。
【详解】根据轴对称图形的意义可知:从左图中可以剪出。原题说法正确;
故答案为:√
【点睛】此题主要考查轴对称图形的意义。
18.见详解
【分析】(1)在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;观察图形可知,要得到一棵完整的松树,那么棵松树的对称轴在树干中间,所以能得到一棵完整的松树的是第二个。
(2)剪纸打开后是一个轴对称图形,第一种是六边形,第二种是五边形。
【详解】(1)
(2)
【点睛】此题主要考查的是轴对称的剪纸问题,要理解轴对称的概念。
19.圈第1个图形
【详解】略
20.图见详解
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】由分析可得:能得到一棵完整的松树的是第二个。
【点睛】此题考查了轴对称的意义及在实际当中的运用。
21.( )( )(○)
【详解】题中第一幅图剪出的是3个完整的小人,但是这3个小人没有手拉手;第二幅图最左边和最右边分别是半个小人;第三幅图剪出的题3个手拉手的小人。
22.(1)轴对称;1;2;三
(2)见详解
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。观察发现,每个小人都是轴对称图形,这4个小人是一样的,而且是手拉着手的,所以剪的时候不能剪断。剪1个小人,可以用1张纸对折,沿着连在一起的边画出半个小人剪开即可。剪2个小人,需要对折两次,如果对折三次,就可以剪出4个小人。
【详解】分析与解答:(1)每一个单独的小人都是一个轴对称图形,要剪出一个这样的小人需要把纸张对折1次。如果把纸张对折两次可以剪出2个这样的手拉手的小人;如果要剪出4个这样的手拉手的小人,需要把纸张对折三次。
(2)我会两种折法,第一种:可以将纸对折,在对折的基础上再同方向对折两次。第二种:将纸进行正反方向对折,未开口的方向要折出四个折痕,然后画出图形剪出即可;画图时,要注意沿着连着一起的边画,否则,会剪出半个人出来。(如图)
【点睛】本题考查轴对称图形的认识及剪法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.4《轴对称的剪纸问题》同步练习
班级:_________ 姓名:__________
一、选择题
1.下面图案( )是从上面剪下来的。
A. B. C.
2.是从对折的( )上剪下来的。
A. B. C.
3.将空白部分剪掉,余下的部分是( )。
A. B. C.
4.按下图的顺序操作,剪下并展开后得到的图形是( )号。
A. B. C. D.
5.按来剪,剪出( )图形;按来剪,剪出( )图形。
① ② ③
A.①② B.①③ C.③②
二、填空题
6.剪一剪。
像上面这样,先把一张纸对折,再画一画、剪一剪。
分析与解答:像这样剪出来的图形都是( )的,它们都是( )。
7.折一折、画一画、剪一剪,看看剪成的图形像什么。
像( )
像( )
8.明明在对折好的纸上剪了两个洞,展开后是哪幅图?画“√”。
9.把一张长方形的纸连续对折3次,并画出蝴蝶的对称部分之后再剪一剪,能剪出( )只完整的蝴蝶。
10.在进行图案制作时,把纸张对折一次可以剪出( )个图案,对折两次可以剪出( )个相同的图案,要剪出4个相同的图案需要对折( )次。
11.下面哪种画法可以剪出3个完整的笑脸?在括号里画“√”。
( )
( )
12.小明和小红都在剪纸。有以下两种剪法,请你选一选。(填序号)
A. 小明剪出的图案如下,他用的是剪法( )。 小红剪出的图案如下,她用的是剪法( )。
B.
三、判断题
13.图形是从下面对折后的纸上剪下来的。( )
14.是从对折剪下来的。( )
15.是从下面对折的纸上剪下来的。( )
16.剪两个手拉手小纸人要对折1次。( )
17.从左图中可以剪出。( )
四、作图题
18.想一想,圈一圈。
(1)如图,把一张正方形纸对折,沿虚线剪,能得到一棵完整的松树的是哪一个?
(2)要想得到六边形,下列哪种剪法是正确的?
19.按照下面的方式折、画、剪(并描出眼睛),得到的是哪幅图?请圈一圈。
20.想一想,圈一圈。
如图,把一张正方形纸对折,沿虚线剪,能得到一棵完整的松树的是哪一个?
五、解答题
21.下面哪种剪法能剪出3个手拉手的小人?请在( )里画“○”。剪一剪,验证你的想法是否正确。
( )( )( )
22.如下图,自己试着用剪刀剪出4个手拉手的小人。
分析与解答:(1)每一个单独的小人都是一个( )图形,要剪出一个这样的小人需要把纸张对折( )次。如果把纸张对折两次可以剪出( )个这样的手拉手的小人;如果要剪出4个这样的手拉手的小人,需要把纸张对折( )次。
你有几种折纸的方法?自己试着折一折,并剪一剪。
参考答案:
1.B
【分析】找到剪下来的图案与原长方形空白的图案相吻合的,就是从原长方形上面剪下来的。
【详解】由题意分析得:
图案是从上面剪下来的。
故答案为:B
2.B
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】是从对折的上剪下来的;
故答案为:B
【点睛】此题考查了轴对称的意义及在实际当中的运用。
3.A
【分析】依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,据此即可进行解答。
【详解】将空白部分剪掉,余下的部分是。
故答案为:A
【点睛】此题主要考查轴对称图形的意义及认识。
4.A
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】由图分析,剪开后的图形应为对称图形且沿对折线对称,由于排除B、D在观察海豚的嘴离对折线很近,则展开后的图上左右两边海豚嘴也应很近,所以排除C,故选A。
【点睛】此题考查了轴对称的意义及在实际当中的运用。
5.C
【分析】轴对称图形是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴,据此解答。
【详解】按 来剪,剪出()图形;按来剪,剪出( )图形。
故答案为:C
【点睛】本题主要考查了根据轴对称图形剪纸的应用。
6. 对称 轴对称图形
【分析】如果沿某条直线对折,对折的两部分是完全重合的,这样的图形为轴对称图形。这条直线叫做这个图形的对称轴。
【详解】像题干中这样剪出来的图形都是对称的,它们都是轴对称图形。
【点睛】熟练掌握轴对称图形的定义是解题关键。
7. 树 人
【解析】略
8.
【详解】略
9.4
【分析】对折3次能把纸分成2×2×2=4×2=8份,每2份剪出1只完整蝴蝶,所以共剪出8÷2=4只完整的蝴蝶。
【详解】根据分析可知:把一张长方形的纸连续对折3次,并画出蝴蝶的对称部分之后再剪一剪,能剪出(4)只完整的蝴蝶。
【点睛】题中利用了轴对称只画了半只蝴蝶,因此要把分成的份数除以2。
10. 1 2 3
【分析】对折一次是把纸分成两份,每一份是半个图案,所以能剪出一个图案,以此类推,对折2次就是把纸分成了4份,也就是可以剪出2个相同的图案,对折3次就是把纸给分成了8份,可以剪出4个相同的图案。
【详解】在进行图案制作时,把纸张对折一次可以剪出(1)个图案,对折两次可以剪出(2)个相同的图案,要剪出4个相同的图案需要对折(3)次。
【点睛】本题主要考查学生对轴对称图形的认识和对“对折”概念的理解。解决此题时如果不理解,也可以具体操作一下。
11.( )(√)
【解析】略
12. B A
【解析】略
13.×
【详解】略
14.√
【详解】略
15.×
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可。
【详解】
如图所示,是从这样对折的纸上剪下来的。
故答案为:×
【点睛】解答此题的依据是:轴对称图形的概念及特征。
。
16.×
【分析】要想剪出两个手拉手小纸人,应将纸对折2次,把这张纸平均分成4份,在对折好的纸上剪出一半的小纸人,则4个一半的小纸人可以组成两个手拉手小纸人。据此判断。
【详解】剪两个手拉手小纸人要对折2次。说法错误。
故答案为:×
【点睛】本题考查轴对称的剪纸问题,应亲自动手剪一剪,即可得出结论。
17.√
【分析】依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,据此即可进行解答。
【详解】根据轴对称图形的意义可知:从左图中可以剪出。原题说法正确;
故答案为:√
【点睛】此题主要考查轴对称图形的意义。
18.见详解
【分析】(1)在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;观察图形可知,要得到一棵完整的松树,那么棵松树的对称轴在树干中间,所以能得到一棵完整的松树的是第二个。
(2)剪纸打开后是一个轴对称图形,第一种是六边形,第二种是五边形。
【详解】(1)
(2)
【点睛】此题主要考查的是轴对称的剪纸问题,要理解轴对称的概念。
19.圈第1个图形
【详解】略
20.图见详解
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】由分析可得:能得到一棵完整的松树的是第二个。
【点睛】此题考查了轴对称的意义及在实际当中的运用。
21.( )( )(○)
【详解】题中第一幅图剪出的是3个完整的小人,但是这3个小人没有手拉手;第二幅图最左边和最右边分别是半个小人;第三幅图剪出的题3个手拉手的小人。
22.(1)轴对称;1;2;三
(2)见详解
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。观察发现,每个小人都是轴对称图形,这4个小人是一样的,而且是手拉着手的,所以剪的时候不能剪断。剪1个小人,可以用1张纸对折,沿着连在一起的边画出半个小人剪开即可。剪2个小人,需要对折两次,如果对折三次,就可以剪出4个小人。
【详解】分析与解答:(1)每一个单独的小人都是一个轴对称图形,要剪出一个这样的小人需要把纸张对折1次。如果把纸张对折两次可以剪出2个这样的手拉手的小人;如果要剪出4个这样的手拉手的小人,需要把纸张对折三次。
(2)我会两种折法,第一种:可以将纸对折,在对折的基础上再同方向对折两次。第二种:将纸进行正反方向对折,未开口的方向要折出四个折痕,然后画出图形剪出即可;画图时,要注意沿着连着一起的边画,否则,会剪出半个人出来。(如图)
【点睛】本题考查轴对称图形的认识及剪法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
