2.5 第5课时 用“边边边”判定三角形全等 学案(含答案)数学湘教版八年级上册
文档属性
| 名称 | 2.5 第5课时 用“边边边”判定三角形全等 学案(含答案)数学湘教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 114.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 15:22:50 | ||
图片预览


文档简介
2.5 第5课时 用“边边边”判定三角形全等
素养目标
1.能说出三角形全等的判定定理“边边边”的内容,能用数学语言表示这个判定定理.
2.能利用“边边边”判定两个三角形全等,并能利用这个定理进行简单的推理与计算.
3.知道三角形具有稳定性,能在实际生活中进行简单应用.
◎重点:全等三角形“边边边”的判定方法及应用.
预习导学
知识点一 全等三角形的判定方法4“边边边”
阅读课本本课时“例8”及其前面的内容,解决下列问题.
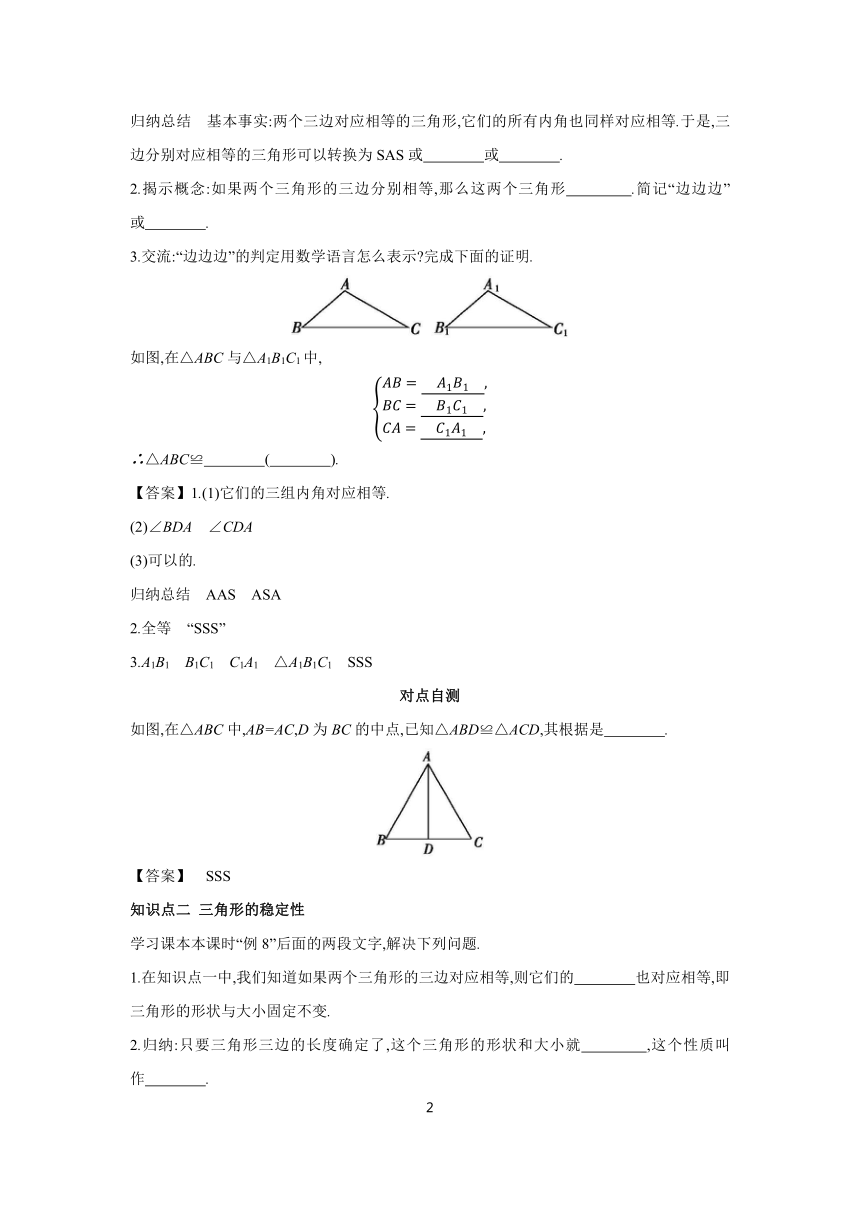
1.课堂操作:(1)下面是两个三边对应相等的三角形,即AB=DE,AC=DF,BC=EF,用量角器分别量一量它们的三个内角,你能发现什么
(2)将上图中的三角形DEF沿EF进行翻折,并将边BC与EF重合在一起,可得下图,连接AD.
由AB=BD,可得∠BAD= ;由AC=CD,可得∠CAD= ,于是,得到这两个三角形的一对内角对应相等.
(3)你能类比(2)中的办法说明△ABC与△DEF其他的两组内角对应相等吗
归纳总结 基本事实:两个三边对应相等的三角形,它们的所有内角也同样对应相等.于是,三边分别对应相等的三角形可以转换为SAS或 或 .
2.揭示概念:如果两个三角形的三边分别相等,那么这两个三角形 .简记“边边边”或 .
3.交流:“边边边”的判定用数学语言怎么表示 完成下面的证明.
如图,在△ABC与△A1B1C1中,
∴△ABC≌ ( ).
【答案】1.(1)它们的三组内角对应相等.
(2)∠BDA ∠CDA
(3)可以的.
归纳总结 AAS ASA
2.全等 “SSS”
3.A1B1 B1C1 C1A1 △A1B1C1 SSS
对点自测
如图,在△ABC中,AB=AC,D为BC的中点,已知△ABD≌△ACD,其根据是 .
【答案】 SSS
知识点二 三角形的稳定性
学习课本本课时“例8”后面的两段文字,解决下列问题.
1.在知识点一中,我们知道如果两个三角形的三边对应相等,则它们的 也对应相等,即三角形的形状与大小固定不变.
2.归纳:只要三角形三边的长度确定了,这个三角形的形状和大小就 ,这个性质叫作 .
3.讨论:三角形的稳定性在现实生活中有着广泛的应用,你能找出来哪些
【答案】1.内角
2.完全确定 三角形的稳定性
3.答案不唯一,自行车的三角形车架、木工师傅在做好门框后在门边上钉上两条斜拉的木条、斜拉桥上的三角形结构等等.
合作探究
任务驱动一
1.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论不正确的是 ( )
A.△MPN≌△MQN
B.∠PMN=∠QMN
C.MQ=NQ
D.∠MPN=∠MQN
【答案】1.C
任务驱动二
2.如图,在生活中,把自行车的几根主梁做成三角形的支架,这是因为三角形具有 性.
【答案】2.稳定
任务驱动三 3.如图,这是为一个测平架,AB=AC,在BC中点D挂一个重锤,自然下垂,使用时调整架身,使点A恰好在重锤线上,就说明此时BC处于水平位置,你能说明其中的道理吗
方法归纳交流 利用全等三角形的知识解决实际问题,关键是能够把实际问题转化为 ,通过合理的数学知识进行解决,因此建立 是解决问题的关键.
【答案】3.解:在△ABD和△ACD中,∴△ABD≌△ACD,∴∠ADB=∠ADC,又∵∠BDC=180°,∴∠ADB=90°,即AD与BC垂直,而AD是垂直地面的,所以BC处于水平位置.
方法归纳交流 数学模型 数学模型
任务驱动四 4.如图,在△ABC中,AB=AC,AD是BC边上的中线,找出图中全等的三角形,并简要说明它们为什么全等
变式演练 如图,AB=AC,DB=DC,F是AD的延长线上一点.
求证:(1) ∠ABD=∠ACD;
(2)BF=CF.
【答案】4.解:全等三角形有△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE.由AB=AC,AD=AD,BD=CD,∴△ABD≌△ACD.∴∠BAD=∠CAD,又AB=AC,AE=AE,∴△ABE≌△ACE.∴BE=EC,又DE=DE,BD=CD,∴△BDE≌△CDE.
变式演练 证明:(1)由AB=AC,DB=DC,又AD=AD,所以△ABD≌△ACD,∠ABD=∠ACD.
(2)由(1)得△ABD≌△ACD,所以∠BAD=∠CAD,又AB=AC,AF=AF,所以△ABF≌△ACF,所以BF=CF.
任务驱动五 5.如图,在四边形ABCD中,AB=CB,AD=CD.
求证:∠C=∠A.
变式演练 如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
【答案】5.证明:连接BD(图略).在△ABD和△CBD中,
∵AB=CB,AD=CD,BD=BD,∴△ABD≌△CBD(SSS),∴∠C=∠A.
变式演练 证明:连接AD(图略).
在△ACD和△ABD中,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF.
∵DE⊥AE,DF⊥AF,
∴DE=DF.
2
素养目标
1.能说出三角形全等的判定定理“边边边”的内容,能用数学语言表示这个判定定理.
2.能利用“边边边”判定两个三角形全等,并能利用这个定理进行简单的推理与计算.
3.知道三角形具有稳定性,能在实际生活中进行简单应用.
◎重点:全等三角形“边边边”的判定方法及应用.
预习导学
知识点一 全等三角形的判定方法4“边边边”
阅读课本本课时“例8”及其前面的内容,解决下列问题.
1.课堂操作:(1)下面是两个三边对应相等的三角形,即AB=DE,AC=DF,BC=EF,用量角器分别量一量它们的三个内角,你能发现什么
(2)将上图中的三角形DEF沿EF进行翻折,并将边BC与EF重合在一起,可得下图,连接AD.
由AB=BD,可得∠BAD= ;由AC=CD,可得∠CAD= ,于是,得到这两个三角形的一对内角对应相等.
(3)你能类比(2)中的办法说明△ABC与△DEF其他的两组内角对应相等吗
归纳总结 基本事实:两个三边对应相等的三角形,它们的所有内角也同样对应相等.于是,三边分别对应相等的三角形可以转换为SAS或 或 .
2.揭示概念:如果两个三角形的三边分别相等,那么这两个三角形 .简记“边边边”或 .
3.交流:“边边边”的判定用数学语言怎么表示 完成下面的证明.
如图,在△ABC与△A1B1C1中,
∴△ABC≌ ( ).
【答案】1.(1)它们的三组内角对应相等.
(2)∠BDA ∠CDA
(3)可以的.
归纳总结 AAS ASA
2.全等 “SSS”
3.A1B1 B1C1 C1A1 △A1B1C1 SSS
对点自测
如图,在△ABC中,AB=AC,D为BC的中点,已知△ABD≌△ACD,其根据是 .
【答案】 SSS
知识点二 三角形的稳定性
学习课本本课时“例8”后面的两段文字,解决下列问题.
1.在知识点一中,我们知道如果两个三角形的三边对应相等,则它们的 也对应相等,即三角形的形状与大小固定不变.
2.归纳:只要三角形三边的长度确定了,这个三角形的形状和大小就 ,这个性质叫作 .
3.讨论:三角形的稳定性在现实生活中有着广泛的应用,你能找出来哪些
【答案】1.内角
2.完全确定 三角形的稳定性
3.答案不唯一,自行车的三角形车架、木工师傅在做好门框后在门边上钉上两条斜拉的木条、斜拉桥上的三角形结构等等.
合作探究
任务驱动一
1.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论不正确的是 ( )
A.△MPN≌△MQN
B.∠PMN=∠QMN
C.MQ=NQ
D.∠MPN=∠MQN
【答案】1.C
任务驱动二
2.如图,在生活中,把自行车的几根主梁做成三角形的支架,这是因为三角形具有 性.
【答案】2.稳定
任务驱动三 3.如图,这是为一个测平架,AB=AC,在BC中点D挂一个重锤,自然下垂,使用时调整架身,使点A恰好在重锤线上,就说明此时BC处于水平位置,你能说明其中的道理吗
方法归纳交流 利用全等三角形的知识解决实际问题,关键是能够把实际问题转化为 ,通过合理的数学知识进行解决,因此建立 是解决问题的关键.
【答案】3.解:在△ABD和△ACD中,∴△ABD≌△ACD,∴∠ADB=∠ADC,又∵∠BDC=180°,∴∠ADB=90°,即AD与BC垂直,而AD是垂直地面的,所以BC处于水平位置.
方法归纳交流 数学模型 数学模型
任务驱动四 4.如图,在△ABC中,AB=AC,AD是BC边上的中线,找出图中全等的三角形,并简要说明它们为什么全等
变式演练 如图,AB=AC,DB=DC,F是AD的延长线上一点.
求证:(1) ∠ABD=∠ACD;
(2)BF=CF.
【答案】4.解:全等三角形有△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE.由AB=AC,AD=AD,BD=CD,∴△ABD≌△ACD.∴∠BAD=∠CAD,又AB=AC,AE=AE,∴△ABE≌△ACE.∴BE=EC,又DE=DE,BD=CD,∴△BDE≌△CDE.
变式演练 证明:(1)由AB=AC,DB=DC,又AD=AD,所以△ABD≌△ACD,∠ABD=∠ACD.
(2)由(1)得△ABD≌△ACD,所以∠BAD=∠CAD,又AB=AC,AF=AF,所以△ABF≌△ACF,所以BF=CF.
任务驱动五 5.如图,在四边形ABCD中,AB=CB,AD=CD.
求证:∠C=∠A.
变式演练 如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
【答案】5.证明:连接BD(图略).在△ABD和△CBD中,
∵AB=CB,AD=CD,BD=BD,∴△ABD≌△CBD(SSS),∴∠C=∠A.
变式演练 证明:连接AD(图略).
在△ACD和△ABD中,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF.
∵DE⊥AE,DF⊥AF,
∴DE=DF.
2
同课章节目录
