人教版6下数学 3.3《圆柱的体积》同步练习(含答案)
文档属性
| 名称 | 人教版6下数学 3.3《圆柱的体积》同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 375.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.3《圆柱的体积》同步练习
班级:_________ 姓名:__________
一、选择题
1.底面积是28.26dm2的圆柱体的高增加3dm,体积增加( )dm3。
A.28.26 B.14.13 C.84.78 D.56.52
2.如图,长方形的长是2厘米,宽是1厘米。分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱,这两个圆柱的体积( )。
A.甲大 B.乙大
C.同样大 D.无法判断谁大
3.一个圆柱形玻璃鱼灯,底面直径是20厘米,把里面的一条鱼捞出来后水面下降了0.2厘米,这条鱼的体积是( )立方厘米。
A. B. C. D.
4.妈妈沏了2L花茶用来招待客人。若将这些花茶倒入从里面量得底面积是30cm2、高是10cm的圆柱形水杯里,最多可以倒满( )杯。
A.5 B.6 C.7
5.用一块长21.98厘米、宽18.84厘米的长方形铁皮,配上直径( )厘米的圆形铁皮就可以做成一个容积最大的容器。
A.3.5 B.7 C.3 D.6
二、填空题
6.一根自来水管的内直径是2厘米。如果水流的速度是0.8米/秒,这根水管5分可以流出( )升水。
7.将一个长3厘米,宽2厘米的长方形,如果以长为轴旋转一周,得到一个立体图形是( )。它的表面积是( ),体积是( )。
8.一根圆柱形钢材长70cm,截成3段小圆柱后,表面积增加50.24cm2,这根钢材的体积是( )cm3。
9.一个圆柱形铁皮油桶,底面周长是188.4cm,高是80cm。如果每升柴油重0.8kg,那么这个油桶可以装( )kg柴油。(油桶厚度忽略不计)
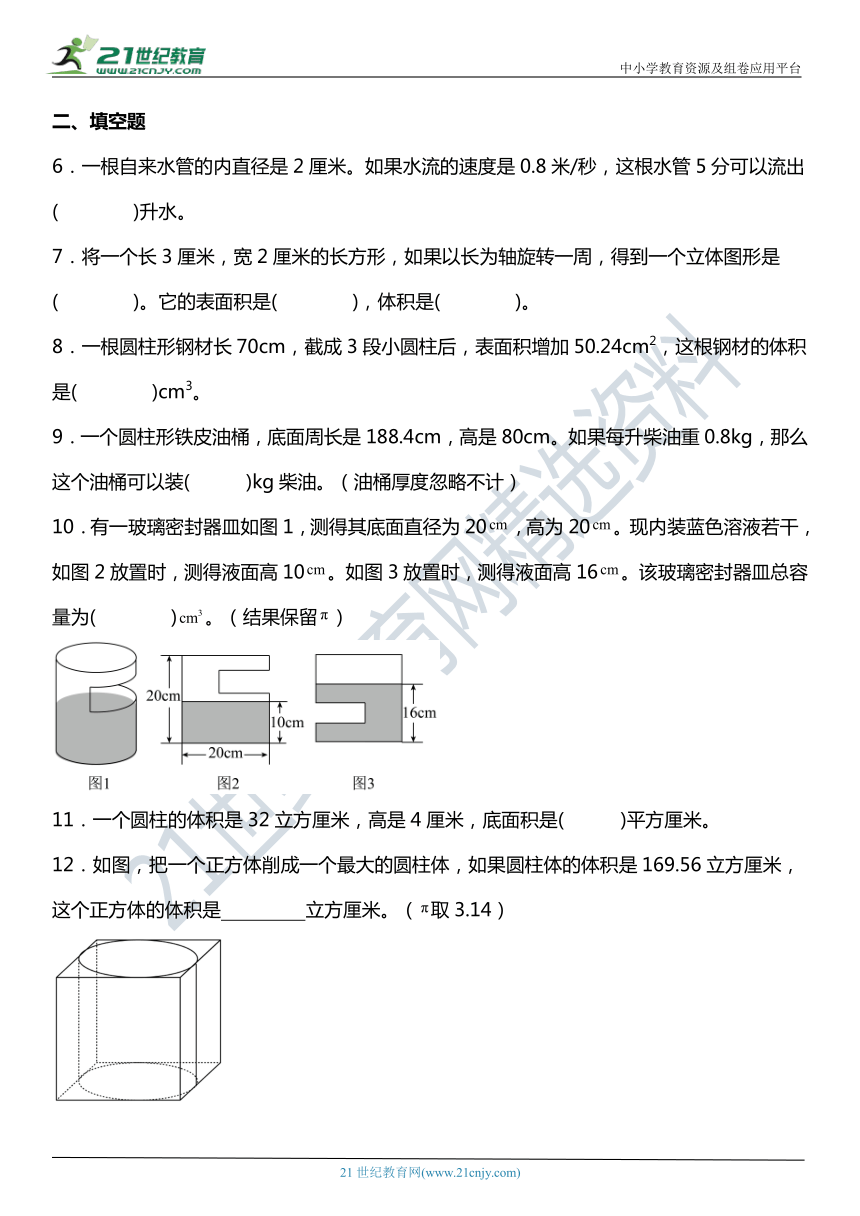
10.有一玻璃密封器皿如图1,测得其底面直径为20,高为20。现内装蓝色溶液若干,如图2放置时,测得液面高10。如图3放置时,测得液面高16。该玻璃密封器皿总容量为( )。(结果保留)
11.一个圆柱的体积是32立方厘米,高是4厘米,底面积是( )平方厘米。
12.如图,把一个正方体削成一个最大的圆柱体,如果圆柱体的体积是169.56立方厘米,这个正方体的体积是 立方厘米。(取3.14)
三、判断题
13.用两张完全一样的长方形纸可卷成两个不同的圆柱,两个圆柱的体积相等。( )
14.两个体积相等圆柱,侧面积一定相等。( )
15.长方体、正方体和圆柱都可以用底面积乘高来求体积。( )
16.圆柱的底面直径扩大2倍,高不变,它的体积就扩大两倍。( )
17.一个圆柱和一个长方体等底等高时,长方体的体积大。( )
四、计算题
18.计算下面各圆柱的体积。(单位:厘米)
五、解答题
19.一个装水的圆柱形容器的底面内直径是10厘米,一个铁块完全浸没在这个容器的水中,将铁块取出后,水面下降2厘米。这个铁块的体积是多少?
20.一个圆柱形金属零件上有9个圆柱形孔(如图)。这个零件的金属用量大约是多少立方分米?(得数保留两位小数。)
21.一个圆柱形木桶,底面内直径为4分米,桶口距底面最小高度为5分米,最大高度为7分米。这个木桶如图放置时,最多能装多少升水?
22.一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。某地区的土地面积为200平方千米,某日平均降水量为50毫米,该日该地区总降水为多少万立方米?该地区一年绿化用水为200万立方米,这些雨水的25%能满足绿化所需吗?
23.小雨的水壶有一个布套(如图)。
(1)做这个布套至少用了多少布料?
(2)一壶水够1.5升吗?(水壶和布套的厚度忽略不计。)
24.学校计划在一块长10米、宽8米的长方形空地上挖一个尽可能大的圆柱形蓄水池。
(1)如果挖成的水池深5米,这个水池能蓄水多少吨?(每立方米水重1吨)
(2)若在这个水池的侧面和池底抹上一层水泥,抹水泥的面积是多大?
参考答案:
1.C
2.B
3.C
4.B
5.B
6.75.36
7. 圆柱 62.8平方厘米/62.8cm2 37.68立方厘米/37.68cm3
8.879.2
9.180.864
10.
11.8
12.216
13.×
14.×
15.√
16.×
17.×
18.157立方厘米;150.72厘米;401.92立方厘米
19.157立方厘米
20.约0.75立方分米
21.62.8升水
22.1000万立方米;能满足
23.(1)785平方厘米
(2)够
24.(1)251.2吨
(2)175.84平方米
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.3《圆柱的体积》同步练习
班级:_________ 姓名:__________
一、选择题
1.底面积是28.26dm2的圆柱体的高增加3dm,体积增加( )dm3。
A.28.26 B.14.13 C.84.78 D.56.52
2.如图,长方形的长是2厘米,宽是1厘米。分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱,这两个圆柱的体积( )。
A.甲大 B.乙大
C.同样大 D.无法判断谁大
3.一个圆柱形玻璃鱼灯,底面直径是20厘米,把里面的一条鱼捞出来后水面下降了0.2厘米,这条鱼的体积是( )立方厘米。
A. B. C. D.
4.妈妈沏了2L花茶用来招待客人。若将这些花茶倒入从里面量得底面积是30cm2、高是10cm的圆柱形水杯里,最多可以倒满( )杯。
A.5 B.6 C.7
5.用一块长21.98厘米、宽18.84厘米的长方形铁皮,配上直径( )厘米的圆形铁皮就可以做成一个容积最大的容器。
A.3.5 B.7 C.3 D.6
二、填空题
6.一根自来水管的内直径是2厘米。如果水流的速度是0.8米/秒,这根水管5分可以流出( )升水。
7.将一个长3厘米,宽2厘米的长方形,如果以长为轴旋转一周,得到一个立体图形是( )。它的表面积是( ),体积是( )。
8.一根圆柱形钢材长70cm,截成3段小圆柱后,表面积增加50.24cm2,这根钢材的体积是( )cm3。
9.一个圆柱形铁皮油桶,底面周长是188.4cm,高是80cm。如果每升柴油重0.8kg,那么这个油桶可以装( )kg柴油。(油桶厚度忽略不计)
10.有一玻璃密封器皿如图1,测得其底面直径为20,高为20。现内装蓝色溶液若干,如图2放置时,测得液面高10。如图3放置时,测得液面高16。该玻璃密封器皿总容量为( )。(结果保留)
11.一个圆柱的体积是32立方厘米,高是4厘米,底面积是( )平方厘米。
12.如图,把一个正方体削成一个最大的圆柱体,如果圆柱体的体积是169.56立方厘米,这个正方体的体积是 立方厘米。(取3.14)
三、判断题
13.用两张完全一样的长方形纸可卷成两个不同的圆柱,两个圆柱的体积相等。( )
14.两个体积相等圆柱,侧面积一定相等。( )
15.长方体、正方体和圆柱都可以用底面积乘高来求体积。( )
16.圆柱的底面直径扩大2倍,高不变,它的体积就扩大两倍。( )
17.一个圆柱和一个长方体等底等高时,长方体的体积大。( )
四、计算题
18.计算下面各圆柱的体积。(单位:厘米)
五、解答题
19.一个装水的圆柱形容器的底面内直径是10厘米,一个铁块完全浸没在这个容器的水中,将铁块取出后,水面下降2厘米。这个铁块的体积是多少?
20.一个圆柱形金属零件上有9个圆柱形孔(如图)。这个零件的金属用量大约是多少立方分米?(得数保留两位小数。)
21.一个圆柱形木桶,底面内直径为4分米,桶口距底面最小高度为5分米,最大高度为7分米。这个木桶如图放置时,最多能装多少升水?
22.一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。某地区的土地面积为200平方千米,某日平均降水量为50毫米,该日该地区总降水为多少万立方米?该地区一年绿化用水为200万立方米,这些雨水的25%能满足绿化所需吗?
23.小雨的水壶有一个布套(如图)。
(1)做这个布套至少用了多少布料?
(2)一壶水够1.5升吗?(水壶和布套的厚度忽略不计。)
24.学校计划在一块长10米、宽8米的长方形空地上挖一个尽可能大的圆柱形蓄水池。
(1)如果挖成的水池深5米,这个水池能蓄水多少吨?(每立方米水重1吨)
(2)若在这个水池的侧面和池底抹上一层水泥,抹水泥的面积是多大?
参考答案:
1.C
2.B
3.C
4.B
5.B
6.75.36
7. 圆柱 62.8平方厘米/62.8cm2 37.68立方厘米/37.68cm3
8.879.2
9.180.864
10.
11.8
12.216
13.×
14.×
15.√
16.×
17.×
18.157立方厘米;150.72厘米;401.92立方厘米
19.157立方厘米
20.约0.75立方分米
21.62.8升水
22.1000万立方米;能满足
23.(1)785平方厘米
(2)够
24.(1)251.2吨
(2)175.84平方米
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
