第4章 一元一次不等式(组) 复习课 学案(含答案)数学湘教版八年级上册
文档属性
| 名称 | 第4章 一元一次不等式(组) 复习课 学案(含答案)数学湘教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 86.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 14:46:38 | ||
图片预览


文档简介
第4章 一元一次不等式(组) 复习课
复习目标
1.能说出一元一次不等式(组)的概念和基本性质,会解一元一次不等式(组).
2.会用数轴表示一元一次不等式(组)的解集.
3.能根据具体问题中的数量关系,列出一元一次不等式(组)解决实际问题.
◎重点:一元一次不等式(组)的解法及应用.
预习导学
体系建构
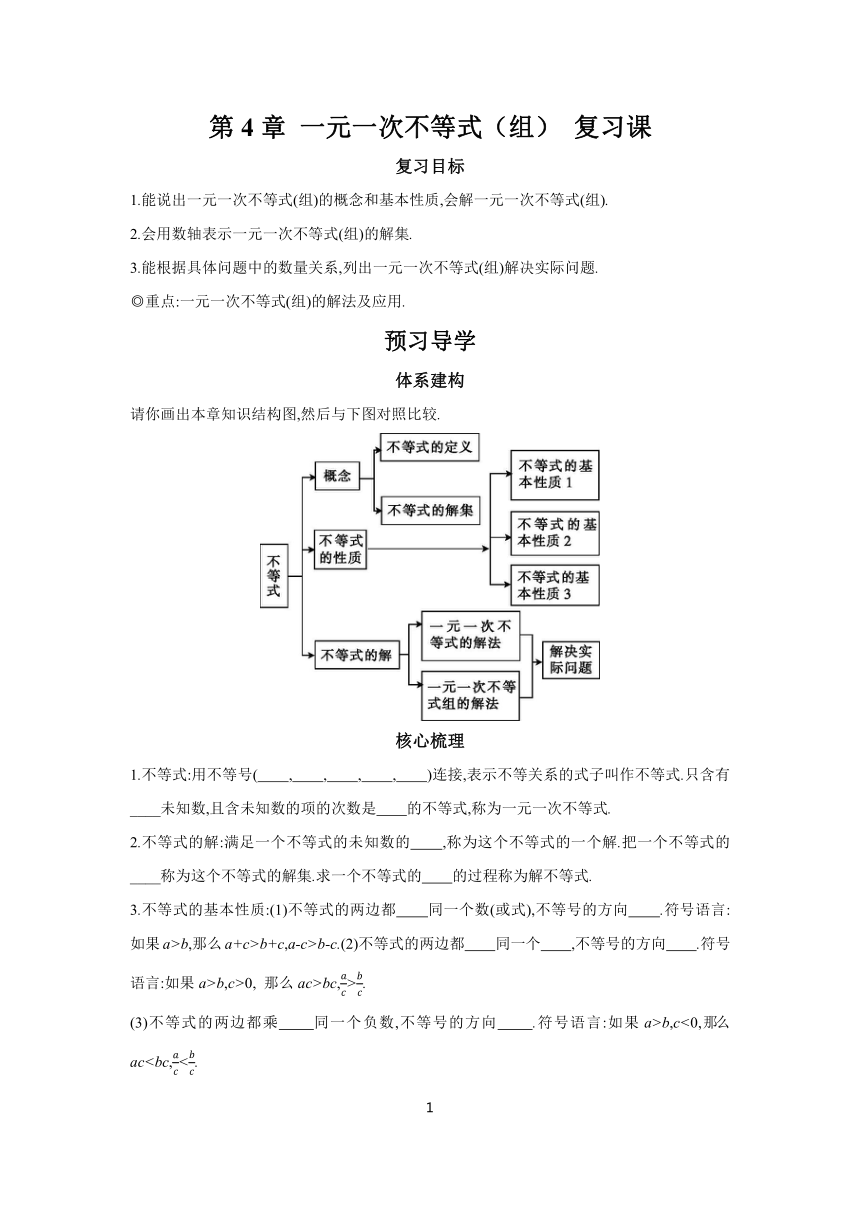
请你画出本章知识结构图,然后与下图对照比较.
核心梳理
1.不等式:用不等号( , , , , )连接,表示不等关系的式子叫作不等式.只含有____未知数,且含未知数的项的次数是 的不等式,称为一元一次不等式.
2.不等式的解:满足一个不等式的未知数的 ,称为这个不等式的一个解.把一个不等式的____称为这个不等式的解集.求一个不等式的 的过程称为解不等式.
3.不等式的基本性质:(1)不等式的两边都 同一个数(或式),不等号的方向 .符号语言:如果a>b,那么a+c>b+c,a-c>b-c.(2)不等式的两边都 同一个 ,不等号的方向 .符号语言:如果a>b,c>0, 那么ac>bc,>.
(3)不等式的两边都乘 同一个负数,不等号的方向 .符号语言:如果a>b,c<0,那么ac4.解一元一次不等式的骤:(1) ;(2) ;(3) ;(4) ;(5) .
5.一元一次不等式组:把含有 未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.几个一元一次不等式解集的 ,叫作由它们所组成的一元一次不等式组的解集.如果没有 ,就说这个不等式组无解.求不等式组的 的过程,叫作解不等式组.
6.解不等式组的一般步骤:(1)分别求出不等式组中 ;
(2)将各不等式的解集在 上表示出来;
(3)在数轴上找出各不等式的解集的 ,这个 就是不等式组的解集.
【答案】1.> < ≥ ≤ ≠ 一个 1
2.每一个值 解的全体 解集
3.(1)加上(或减去) 不变
(2)乘(或除以) 正数 不变
(3)(或除以) 改变
4.(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)化系数为1
5.相同 公共部分 公共部分 解集
6.(1)各不等式的解集
(2)数轴
(3)公共部分 公共部分
合作探究
专题一 列不等式
1.a与2的差是非负数,用不等式表示为 .
【答案】1.a-2≥0
专题二 不等式的性质
2.若a>b,则得到ac【答案】2.c<0
归纳交流 不等式的两边都 同一个负数,不等号的方向 .
【答案】乘(或除以) 改变
变式演练 若a>b,则得到ac2>bc2的条件是 .
【答案】c≠0
专题三 不等式的解与不等式的解集
3.下列说法正确的是 ( )
A.x=4是不等式2x>7的一个解
B.x=4是不等式2x>7的解集
C.不等式2x>7的解集是x>4
D.不等式2x>7的解集是x<4
4.代数式6x2-7的最小值是 ,此时x为 .
【答案】3.A 4.-7 0
专题四 不等式在代数中的综合运用
5.已知|2x-24|+(3x-y-m)2=0中,y是正数,则m的取值范围是 ( )
A.m>36
B.m>12
C.m<12
D.m<36
【答案】5.D
专题五 解不等式(组)
6.解不等式或不等式组.
(1)-(x-1)≥1+-.
(2)
【答案】6.(1)解:4(4x-3)-12(x-1)≥12+2(1-2x)-3(3x-1),
16x-12-12x+12≥12+2-4x-9x+3,
17x≥17,x≥1.
(2)解:解不等式①得x>-,解不等式②得x≥11,
∴不等式组的解集为x≥11.
专题六 求不等式组的整数解
7.求不等式组的整数解.
【答案】7.解:解不等式组得∴不等式组的解集为-1≤x<,
∴不等式组的整数解为-1,0.
2
复习目标
1.能说出一元一次不等式(组)的概念和基本性质,会解一元一次不等式(组).
2.会用数轴表示一元一次不等式(组)的解集.
3.能根据具体问题中的数量关系,列出一元一次不等式(组)解决实际问题.
◎重点:一元一次不等式(组)的解法及应用.
预习导学
体系建构
请你画出本章知识结构图,然后与下图对照比较.
核心梳理
1.不等式:用不等号( , , , , )连接,表示不等关系的式子叫作不等式.只含有____未知数,且含未知数的项的次数是 的不等式,称为一元一次不等式.
2.不等式的解:满足一个不等式的未知数的 ,称为这个不等式的一个解.把一个不等式的____称为这个不等式的解集.求一个不等式的 的过程称为解不等式.
3.不等式的基本性质:(1)不等式的两边都 同一个数(或式),不等号的方向 .符号语言:如果a>b,那么a+c>b+c,a-c>b-c.(2)不等式的两边都 同一个 ,不等号的方向 .符号语言:如果a>b,c>0, 那么ac>bc,>.
(3)不等式的两边都乘 同一个负数,不等号的方向 .符号语言:如果a>b,c<0,那么ac
5.一元一次不等式组:把含有 未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.几个一元一次不等式解集的 ,叫作由它们所组成的一元一次不等式组的解集.如果没有 ,就说这个不等式组无解.求不等式组的 的过程,叫作解不等式组.
6.解不等式组的一般步骤:(1)分别求出不等式组中 ;
(2)将各不等式的解集在 上表示出来;
(3)在数轴上找出各不等式的解集的 ,这个 就是不等式组的解集.
【答案】1.> < ≥ ≤ ≠ 一个 1
2.每一个值 解的全体 解集
3.(1)加上(或减去) 不变
(2)乘(或除以) 正数 不变
(3)(或除以) 改变
4.(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)化系数为1
5.相同 公共部分 公共部分 解集
6.(1)各不等式的解集
(2)数轴
(3)公共部分 公共部分
合作探究
专题一 列不等式
1.a与2的差是非负数,用不等式表示为 .
【答案】1.a-2≥0
专题二 不等式的性质
2.若a>b,则得到ac
归纳交流 不等式的两边都 同一个负数,不等号的方向 .
【答案】乘(或除以) 改变
变式演练 若a>b,则得到ac2>bc2的条件是 .
【答案】c≠0
专题三 不等式的解与不等式的解集
3.下列说法正确的是 ( )
A.x=4是不等式2x>7的一个解
B.x=4是不等式2x>7的解集
C.不等式2x>7的解集是x>4
D.不等式2x>7的解集是x<4
4.代数式6x2-7的最小值是 ,此时x为 .
【答案】3.A 4.-7 0
专题四 不等式在代数中的综合运用
5.已知|2x-24|+(3x-y-m)2=0中,y是正数,则m的取值范围是 ( )
A.m>36
B.m>12
C.m<12
D.m<36
【答案】5.D
专题五 解不等式(组)
6.解不等式或不等式组.
(1)-(x-1)≥1+-.
(2)
【答案】6.(1)解:4(4x-3)-12(x-1)≥12+2(1-2x)-3(3x-1),
16x-12-12x+12≥12+2-4x-9x+3,
17x≥17,x≥1.
(2)解:解不等式①得x>-,解不等式②得x≥11,
∴不等式组的解集为x≥11.
专题六 求不等式组的整数解
7.求不等式组的整数解.
【答案】7.解:解不等式组得∴不等式组的解集为-1≤x<,
∴不等式组的整数解为-1,0.
2
同课章节目录
