北师大版5下数学3.3《分数乘法(三)》同步练习(含答案)
文档属性
| 名称 | 北师大版5下数学3.3《分数乘法(三)》同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.3《分数乘法(三)》同步练习
班级:_________ 姓名:__________
一、选择题
1.两个分数相乘,其中一个分数扩大到原来的3倍,要使积不变,另外一个分数( )。
A.扩大到原来的3倍 B.扩大到原来的6倍
C.缩小到原来的 D.缩小到原来的
2.《庄子 天下》中有这样一段话:“一尺之棰,日取其半,万世不竭。”意思是说:一根一尺长的木棍,第一天截取它的一半,第二天截取剩下的一半,第三天再截取剩下的一半,……。第四天截取的长度是这根木棍的( )。
A. B. C. D.
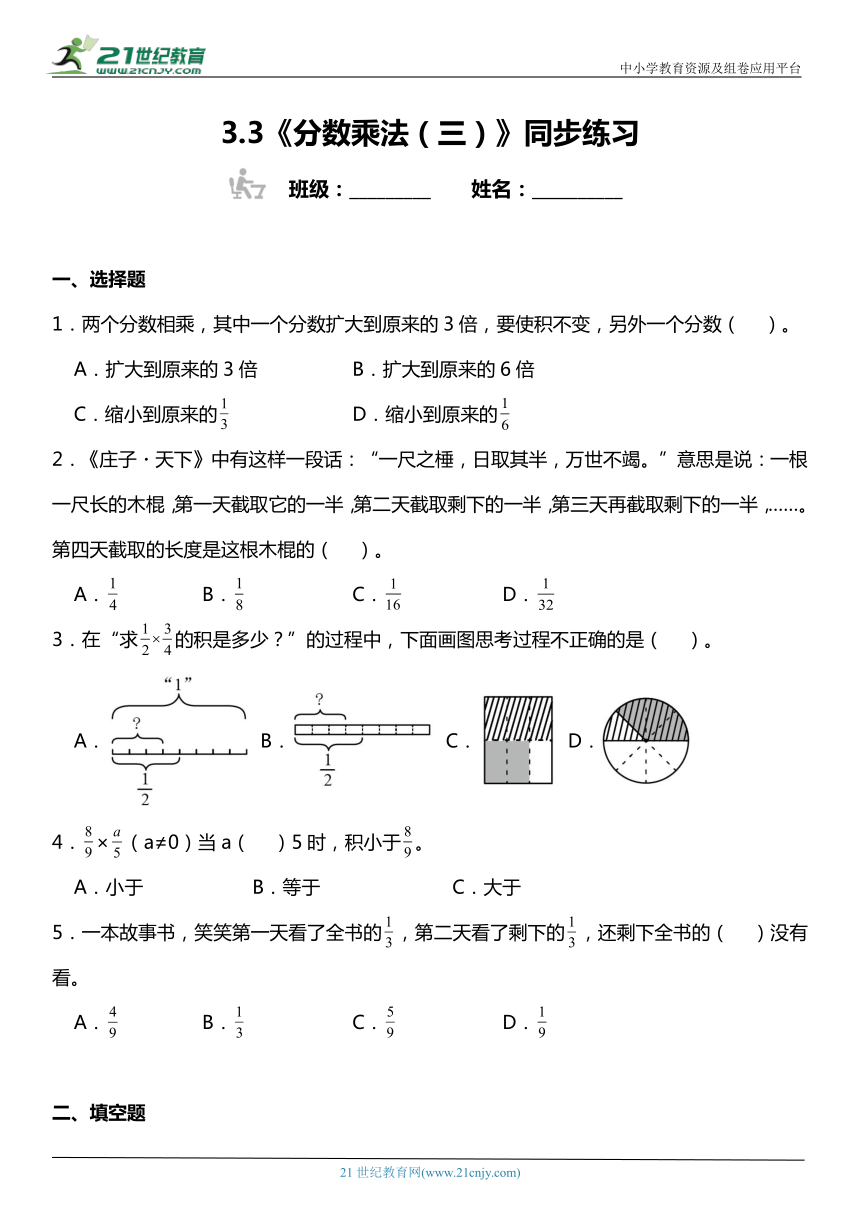
3.在“求的积是多少?”的过程中,下面画图思考过程不正确的是( )。
A. B. C. D.
4.×(a≠0)当a( )5时,积小于。
A.小于 B.等于 C.大于
5.一本故事书,笑笑第一天看了全书的,第二天看了剩下的,还剩下全书的( )没有看。
A. B. C. D.
二、填空题
6.一瓶牛奶重千克,乐乐喝了这瓶牛奶的,妍妍喝了剩下牛奶的。( )喝得多。
7.某公园的是空地,空地的准备铺草坪,铺草坪面积占公园总面积的( )。
8.一根木材,第一次截取米,第二次比第一次多截取,第二次比第一次多截取( )米。
9.在( )里填上“>”“<”或“=”。
×( ) ×( ) ×1( )+1
10.第一根电线长6.5米,用去了,还剩下( )米;第二根电线长5.2米,用去了米,还剩下( )米。
11.千米的是( )千米,比克多克是( )克。
12.一块蛋糕,笑笑第一天吃了它的,第二天吃的相当于第一天的。列式,这个表示( )。
三、判断题
13.一袋饼干共25块,吃了一半,还剩10块。( )
14.小时的是小时。( )
15.3个与3的意义不相同,但是计算结果相同。( )
16.一瓶饮料重千克,喝去,正好喝完。( )
17.若干个真分数相乘的积一定小于任何一个因数。( )
四、计算题
18.直接写出得数。
×20= += -= ×4=
×= ×18= ×= ×=
++= +-=
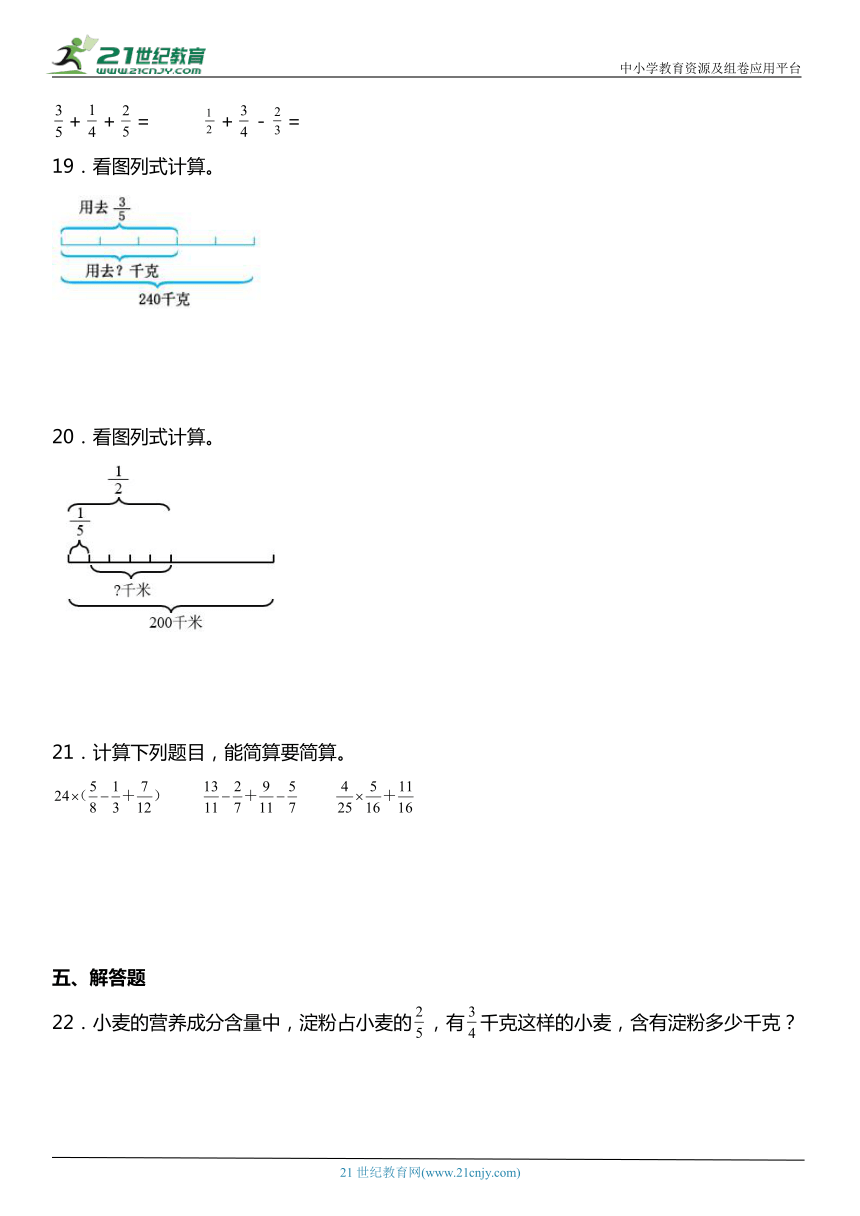
19.看图列式计算。
20.看图列式计算。
21.计算下列题目,能简算要简算。
五、解答题
22.小麦的营养成分含量中,淀粉占小麦的,有千克这样的小麦,含有淀粉多少千克?
23.羊村里的试验田要试种新草,山羊种植的面积是试验田的,绵羊种植的面积是山羊种植面积的。绵羊种的新草占这块试验田的几分之几?
24.一家水果店当天进货水果210斤,上午卖了水果总量的,下午卖的水果重量比上午多,当天的水果卖完了吗?为什么?
25.画一画,涂一涂,算一算。
26.妙妙和爸爸登白露山,用25分钟走了全程的,又用了20分钟走了剩下的,最后用10分钟登上了山顶。
(1)最后10分钟走的路程是全程的几分之几?
(2)这三个时间段,哪一段时间内走得最快?你是怎么想的?
参考答案:
1.C
【分析】根据积的变化规律:如果一个因数扩大几倍,另一个因数缩小它的几分之一,那么积不变;据此解答。
【详解】两个分数相乘,其中一个分数扩大到原来的3倍,要使积不变,另外一个分数缩小到原来的。
故答案为:C
【点睛】利用积的不变规律进行解答。
2.C
【分析】将一尺长的木棍看作单位“1”,用单位“1”乘,求出第一天截取的分率。截取的和剩下的相等。再将第一天剩下的分率看作单位“1”,将其乘,求出第二天截取的分率。据此类推,求出第四天截取的长度是这根木棍的几分之几。
【详解】1××××=
所以,第四天截取的长度是这根木棍的。
故答案为:C
【点睛】本题考查了分数乘法,求一个数的几分之几是多少,用这个数乘分率。
3.C
【分析】“”先将单位“1”平均分成2份,取其中的1份,表示出。再将这个看作单位“1”,再平均分成4份,取其中的3份,即可表示出。
【详解】A.将再看作单位“1”,平均分成了4份,取了其中的3份,能够表示出;
B.将整体看作单位“1”,取其中的一半为。将再看作单位“1”,平均分成了4份,取了其中的3份,能够表示出;
C.这个图不能表示出;
D.先将整个圆看作单位“1”,取半圆为。再将半圆看作单位“1”,平均分成4份,取其中的3份,那么它能表示出。
故答案为:C
【点睛】本题考查了分数乘法,掌握分数乘分数的意义是解题的关键。
4.A
【分析】一个分数乘小于1的分数时,积小于这个分数;一个分数大于1的数时,积大于这个分数。据此可得出答案。
【详解】×(a≠0),当a<5时,此时<1,积小于。
故答案为:A
【点睛】本题主要考查的是分数的意义及大小比较,解题的关键是熟练掌握积与乘数的关系,进而得出答案。
5.A
【分析】把这本故事书的总页数看作单位“1”,第一天看了全书的,则剩下全书的1-=;第二天看了剩下的,即第二天看了的,求一个数的几分之几是多少用乘法计算,用×可求出第二天看了全书的;最后用1减去与的和,可求出还剩全书的几分之几没有看。
【详解】(1-)×
=×
=
1-(+)
=1-(+)
=1-
=
所以,还剩下全书的没有看。
故答案为:A
6.妍妍
【分析】乐乐喝了这瓶牛奶的,那么就剩下1-=,妍妍喝了剩下牛奶的,也就是的,用×=,两个数进行比较即可解答。
【详解】(1-)×
=×
=
=,<
因此可得妍妍喝得多。
一瓶牛奶重千克,乐乐喝了这瓶牛奶的,妍妍喝了剩下牛奶的。妍妍喝得多。
【点睛】此题考查单位“1”的确定,单位“1”不同,即使分率相同,具体的量也不同。
7.
【分析】将公园的总面积看作单位“1”,公园的是空地,求一个数的几分之几是多少,用乘法,用1×可以求出空地的面积;再将空地的面积看作单位“1”,空地的准备铺草坪,即用1××求出铺草坪的面积,据此计算即可。
【详解】由分析可得:
1××
=×
=
综上所述:某公园的是空地,空地的准备铺草坪,铺草坪面积占公园总面积的。
【点睛】本题主要考查了分数乘法的应用,解题的关键是确定单位“1”,求一个数的几分之几是多少,用乘法。
8.
【分析】将第一次截取的长度看作单位“1”,根据分数乘法的意义,求一个数的几分之几用乘法,即用乘可得第二次比第一次多截取的米数。
【详解】由分析可得:
×=(米)
综上所述:一根木材,第一次截取米,第二次比第一次多截取,第二次比第一次多截取米。
【点睛】本题主要考查了分数乘法的应用,解题的关键是确定单位“1”,求一个数的几分之几是多少,用乘法。
9. < > <
【分析】一个非零数,乘大于1的数积大于这个数;乘小于1的数积小于这个数;乘等于1的数,积等于这个数;据此解答。
【详解】<1,所以×<;
>1,所以×>;
×1=<+1
【点睛】解答本题的关键是理解积与因数的关系。
10. 1.3 4.45
【分析】由于用去了,用去了这根电线的,单位“1”是这根电线厂,单位“1”已知,用乘法,即6.5×,再用6.5减去用去的长度即可;第二根电线用去了米,用总长度减去即可求出剩下的。
【详解】6.5-6.5×
=6.5-5.2
=1.3(米)
5.2-=4.45(米)
第一根电线长6.5米,用去了,还剩下1.3米;第二根电线长5.2米,用去了米,还剩下4.45米。
【点睛】本题主要考查分数乘法的应用,求一个数的几分之几是多少,用乘法;同时要注意,分数后面加单位表示具体的数。
11. /1
【分析】求一个数的几分之几是多少,用乘法计算,据此用乘即可求出未知米数;求比克多克是多少克,用加法即可解答。
【详解】×=(米)
+=(克)
千米的是千米,比克多克是克。
【点睛】本题考查了分数乘法和加法的运算。掌握分数乘法的意义是解题的关键。
12.第二天吃的蛋糕量
【分析】将这块蛋糕看作单位“1”,第一天吃了它的,求一个数的几分之几是多少,用乘法,用1×可以求出第一天吃的蛋糕量;再将第一天吃的量看作单位“1”,第二天吃的相当于第一天的,即用×求出第二天吃的量,据此分析即可。
【详解】由分析可得:
第一天吃的量:1×=
第二天吃的量:
所以表示第二天吃的蛋糕量。
综上所述:一块蛋糕,笑笑第一天吃了它的,第二天吃的相当于第一天的。列式,这个表示第二天吃的蛋糕量。
【点睛】本题主要考查了分数乘法的应用,解题的关键是确定单位“1”,求一个数的几分之几是多少,用乘法。
13.×
【分析】根据题意,“吃了一半”可表示为吃了,则还剩下(1-),求一个数的几分之几用乘法计算。
【详解】25×(1-)
=25×
=12.5(块)
所以“一袋饼干共25块,吃了一半,还剩10块”的说法错误。
故答案为:×
【点睛】本题考查的是求一个数的几分之几,用乘法计算。
14.√
【分析】求一个数的几分之几是多少,用乘法计算,据此列式解答。
【详解】×=(小时),原题说法正确。
故答案为:√
【点睛】分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母。
15.√
【分析】3个表示3个相加的和是多少,可列式为×3;3的表示将3分成6份,求其中的5份是多少,可列式为3×。计算比较即可。
【详解】3个列式计算:×3=
3的列式计算:3×=
所以意义不同,但计算结果相同。
故答案为:√
【点睛】本题考查了分数的意义及分数乘法的意义的应用。
16.×
【分析】将这瓶饮料总量看作单位“1”,喝去后,根据分数减法的意义,还剩下全部的“1-=”,求一个数的几分之几是多少,用乘法,所以还剩下×=(千克),据此判断。
【详解】由分析可知:
1-=
×=(千克)
所以一瓶饮料重千克,喝去还剩下千克;
故答案为:×
【点睛】本题分数的应用,注意:前后两个分数的不同,前一个表示具体数量,后一个表示占全部的分率。
17.√
【分析】真分数都小于1,根据一个数乘一个小于1的数,积小于第一个因数,判断对错即可。
【详解】举例说明:
=
=
所以原题干说法正确。
故答案为:√
【点睛】本题解题的关键是知道真分数都小于1,熟练掌握在乘法算式中,积与因数大小关系的判断。
18.12;;;;
;4;;;
;
【详解】略
19.144千克
【分析】由图形可知,单位“1”是总的千克数,是240千克,求它的是多少,用乘法计算即可解答。
【详解】240×=144(千克)
20.80千米
【分析】由图形可知,单位“1”是总的千米数,是200千米,求它的几分之几是多少,用乘法计算。先求出单位“1”的,再求出剩下部分的,即可解答。
【详解】200××(1-)
=100×
=80(千米)
21.21;1;
【分析】,根据乘法分配律,将算式变为进行简算即可;
,根据加法交换律和减法的性质,将算式变为)进行简算即可;
,先计算出乘法,再计算出加法。
【详解】
)
22.千克
【分析】把小麦的质量看作单位“1”,根据分数乘法的意义,用小麦的质量乘,即可计算出千克这样的小麦,含有淀粉多少千克。
【详解】×=(千克)
答:有千克这样的小麦,含有淀粉千克。
【点睛】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
23.
【分析】把这块试验田的总面积看作单位“1”,是山羊种植的面积所占总面积的分率,已知绵羊种植的面积是山羊种植面积的,用乘即绵羊种植的面积所占总面积的分率。
【详解】×
答:绵羊种的新草占这块试验田的。
【点睛】本题考查了学生完成简单的分数乘法应用题的能力。
24.当天的水果卖完了,原因见详解。
【分析】把水果总量看作单位“1”,先求出下午卖的水果重量占全部的分率,再加上午卖了水果总量的分率,与“1”比较即可。
【详解】
=
=
答:当天的水果卖完了。下午卖的水果相当于水果总量的,加上上午卖的水果总量的,正好是全部水果量。
【点睛】本题主要考查了分数四则复合应用题,解题的关键是求出上午和下午卖的分率和。
25.;图见详解
【分析】把长方形看作单位“1”,平均分成6份,取其中的5份涂色,再把涂色部分看作单位“1”,平均分成4份,取其中的1份涂色,即表示×,据此解答。
【详解】×=
【点睛】本题主要考查两个分数相乘的意义,通过画图可以更直观的了解。
26.(1)是全程的;
(2)最后10分钟走得最快,见详解
【分析】(1)把全程看作单位“1”,全程分成3段,第一段占全程的,第二段占剩下的,最后10分钟占剩下的,用1-即剩下的占全程的分率,再乘即最后10分钟走的路程是全程的几分之几。
(2)先依据速度=路程÷时间,分别求出三种情况下的速度,再根据分数大小比较方法即可解答。
【详解】(1)(1-)×
=×
=
答:最后10分钟走的路程是全程的。
(2)÷25
=×
=
÷20
=×
=
÷10
=×
=
<<
前25分钟平均每分钟行驶总路程的,中间20分钟平均每分钟行驶总路程的,最后10分钟平均每分钟行驶总路程的,最后10分钟走得快。
答:最后10分钟走得最快;同分子分数比较大小时,分子相同时,分母小的分数大。
【点睛】此题的解题关键是确定单位“1”,利用分数加减法的意义求出结果。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.3《分数乘法(三)》同步练习
班级:_________ 姓名:__________
一、选择题
1.两个分数相乘,其中一个分数扩大到原来的3倍,要使积不变,另外一个分数( )。
A.扩大到原来的3倍 B.扩大到原来的6倍
C.缩小到原来的 D.缩小到原来的
2.《庄子 天下》中有这样一段话:“一尺之棰,日取其半,万世不竭。”意思是说:一根一尺长的木棍,第一天截取它的一半,第二天截取剩下的一半,第三天再截取剩下的一半,……。第四天截取的长度是这根木棍的( )。
A. B. C. D.
3.在“求的积是多少?”的过程中,下面画图思考过程不正确的是( )。
A. B. C. D.
4.×(a≠0)当a( )5时,积小于。
A.小于 B.等于 C.大于
5.一本故事书,笑笑第一天看了全书的,第二天看了剩下的,还剩下全书的( )没有看。
A. B. C. D.
二、填空题
6.一瓶牛奶重千克,乐乐喝了这瓶牛奶的,妍妍喝了剩下牛奶的。( )喝得多。
7.某公园的是空地,空地的准备铺草坪,铺草坪面积占公园总面积的( )。
8.一根木材,第一次截取米,第二次比第一次多截取,第二次比第一次多截取( )米。
9.在( )里填上“>”“<”或“=”。
×( ) ×( ) ×1( )+1
10.第一根电线长6.5米,用去了,还剩下( )米;第二根电线长5.2米,用去了米,还剩下( )米。
11.千米的是( )千米,比克多克是( )克。
12.一块蛋糕,笑笑第一天吃了它的,第二天吃的相当于第一天的。列式,这个表示( )。
三、判断题
13.一袋饼干共25块,吃了一半,还剩10块。( )
14.小时的是小时。( )
15.3个与3的意义不相同,但是计算结果相同。( )
16.一瓶饮料重千克,喝去,正好喝完。( )
17.若干个真分数相乘的积一定小于任何一个因数。( )
四、计算题
18.直接写出得数。
×20= += -= ×4=
×= ×18= ×= ×=
++= +-=
19.看图列式计算。
20.看图列式计算。
21.计算下列题目,能简算要简算。
五、解答题
22.小麦的营养成分含量中,淀粉占小麦的,有千克这样的小麦,含有淀粉多少千克?
23.羊村里的试验田要试种新草,山羊种植的面积是试验田的,绵羊种植的面积是山羊种植面积的。绵羊种的新草占这块试验田的几分之几?
24.一家水果店当天进货水果210斤,上午卖了水果总量的,下午卖的水果重量比上午多,当天的水果卖完了吗?为什么?
25.画一画,涂一涂,算一算。
26.妙妙和爸爸登白露山,用25分钟走了全程的,又用了20分钟走了剩下的,最后用10分钟登上了山顶。
(1)最后10分钟走的路程是全程的几分之几?
(2)这三个时间段,哪一段时间内走得最快?你是怎么想的?
参考答案:
1.C
【分析】根据积的变化规律:如果一个因数扩大几倍,另一个因数缩小它的几分之一,那么积不变;据此解答。
【详解】两个分数相乘,其中一个分数扩大到原来的3倍,要使积不变,另外一个分数缩小到原来的。
故答案为:C
【点睛】利用积的不变规律进行解答。
2.C
【分析】将一尺长的木棍看作单位“1”,用单位“1”乘,求出第一天截取的分率。截取的和剩下的相等。再将第一天剩下的分率看作单位“1”,将其乘,求出第二天截取的分率。据此类推,求出第四天截取的长度是这根木棍的几分之几。
【详解】1××××=
所以,第四天截取的长度是这根木棍的。
故答案为:C
【点睛】本题考查了分数乘法,求一个数的几分之几是多少,用这个数乘分率。
3.C
【分析】“”先将单位“1”平均分成2份,取其中的1份,表示出。再将这个看作单位“1”,再平均分成4份,取其中的3份,即可表示出。
【详解】A.将再看作单位“1”,平均分成了4份,取了其中的3份,能够表示出;
B.将整体看作单位“1”,取其中的一半为。将再看作单位“1”,平均分成了4份,取了其中的3份,能够表示出;
C.这个图不能表示出;
D.先将整个圆看作单位“1”,取半圆为。再将半圆看作单位“1”,平均分成4份,取其中的3份,那么它能表示出。
故答案为:C
【点睛】本题考查了分数乘法,掌握分数乘分数的意义是解题的关键。
4.A
【分析】一个分数乘小于1的分数时,积小于这个分数;一个分数大于1的数时,积大于这个分数。据此可得出答案。
【详解】×(a≠0),当a<5时,此时<1,积小于。
故答案为:A
【点睛】本题主要考查的是分数的意义及大小比较,解题的关键是熟练掌握积与乘数的关系,进而得出答案。
5.A
【分析】把这本故事书的总页数看作单位“1”,第一天看了全书的,则剩下全书的1-=;第二天看了剩下的,即第二天看了的,求一个数的几分之几是多少用乘法计算,用×可求出第二天看了全书的;最后用1减去与的和,可求出还剩全书的几分之几没有看。
【详解】(1-)×
=×
=
1-(+)
=1-(+)
=1-
=
所以,还剩下全书的没有看。
故答案为:A
6.妍妍
【分析】乐乐喝了这瓶牛奶的,那么就剩下1-=,妍妍喝了剩下牛奶的,也就是的,用×=,两个数进行比较即可解答。
【详解】(1-)×
=×
=
=,<
因此可得妍妍喝得多。
一瓶牛奶重千克,乐乐喝了这瓶牛奶的,妍妍喝了剩下牛奶的。妍妍喝得多。
【点睛】此题考查单位“1”的确定,单位“1”不同,即使分率相同,具体的量也不同。
7.
【分析】将公园的总面积看作单位“1”,公园的是空地,求一个数的几分之几是多少,用乘法,用1×可以求出空地的面积;再将空地的面积看作单位“1”,空地的准备铺草坪,即用1××求出铺草坪的面积,据此计算即可。
【详解】由分析可得:
1××
=×
=
综上所述:某公园的是空地,空地的准备铺草坪,铺草坪面积占公园总面积的。
【点睛】本题主要考查了分数乘法的应用,解题的关键是确定单位“1”,求一个数的几分之几是多少,用乘法。
8.
【分析】将第一次截取的长度看作单位“1”,根据分数乘法的意义,求一个数的几分之几用乘法,即用乘可得第二次比第一次多截取的米数。
【详解】由分析可得:
×=(米)
综上所述:一根木材,第一次截取米,第二次比第一次多截取,第二次比第一次多截取米。
【点睛】本题主要考查了分数乘法的应用,解题的关键是确定单位“1”,求一个数的几分之几是多少,用乘法。
9. < > <
【分析】一个非零数,乘大于1的数积大于这个数;乘小于1的数积小于这个数;乘等于1的数,积等于这个数;据此解答。
【详解】<1,所以×<;
>1,所以×>;
×1=<+1
【点睛】解答本题的关键是理解积与因数的关系。
10. 1.3 4.45
【分析】由于用去了,用去了这根电线的,单位“1”是这根电线厂,单位“1”已知,用乘法,即6.5×,再用6.5减去用去的长度即可;第二根电线用去了米,用总长度减去即可求出剩下的。
【详解】6.5-6.5×
=6.5-5.2
=1.3(米)
5.2-=4.45(米)
第一根电线长6.5米,用去了,还剩下1.3米;第二根电线长5.2米,用去了米,还剩下4.45米。
【点睛】本题主要考查分数乘法的应用,求一个数的几分之几是多少,用乘法;同时要注意,分数后面加单位表示具体的数。
11. /1
【分析】求一个数的几分之几是多少,用乘法计算,据此用乘即可求出未知米数;求比克多克是多少克,用加法即可解答。
【详解】×=(米)
+=(克)
千米的是千米,比克多克是克。
【点睛】本题考查了分数乘法和加法的运算。掌握分数乘法的意义是解题的关键。
12.第二天吃的蛋糕量
【分析】将这块蛋糕看作单位“1”,第一天吃了它的,求一个数的几分之几是多少,用乘法,用1×可以求出第一天吃的蛋糕量;再将第一天吃的量看作单位“1”,第二天吃的相当于第一天的,即用×求出第二天吃的量,据此分析即可。
【详解】由分析可得:
第一天吃的量:1×=
第二天吃的量:
所以表示第二天吃的蛋糕量。
综上所述:一块蛋糕,笑笑第一天吃了它的,第二天吃的相当于第一天的。列式,这个表示第二天吃的蛋糕量。
【点睛】本题主要考查了分数乘法的应用,解题的关键是确定单位“1”,求一个数的几分之几是多少,用乘法。
13.×
【分析】根据题意,“吃了一半”可表示为吃了,则还剩下(1-),求一个数的几分之几用乘法计算。
【详解】25×(1-)
=25×
=12.5(块)
所以“一袋饼干共25块,吃了一半,还剩10块”的说法错误。
故答案为:×
【点睛】本题考查的是求一个数的几分之几,用乘法计算。
14.√
【分析】求一个数的几分之几是多少,用乘法计算,据此列式解答。
【详解】×=(小时),原题说法正确。
故答案为:√
【点睛】分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母。
15.√
【分析】3个表示3个相加的和是多少,可列式为×3;3的表示将3分成6份,求其中的5份是多少,可列式为3×。计算比较即可。
【详解】3个列式计算:×3=
3的列式计算:3×=
所以意义不同,但计算结果相同。
故答案为:√
【点睛】本题考查了分数的意义及分数乘法的意义的应用。
16.×
【分析】将这瓶饮料总量看作单位“1”,喝去后,根据分数减法的意义,还剩下全部的“1-=”,求一个数的几分之几是多少,用乘法,所以还剩下×=(千克),据此判断。
【详解】由分析可知:
1-=
×=(千克)
所以一瓶饮料重千克,喝去还剩下千克;
故答案为:×
【点睛】本题分数的应用,注意:前后两个分数的不同,前一个表示具体数量,后一个表示占全部的分率。
17.√
【分析】真分数都小于1,根据一个数乘一个小于1的数,积小于第一个因数,判断对错即可。
【详解】举例说明:
=
=
所以原题干说法正确。
故答案为:√
【点睛】本题解题的关键是知道真分数都小于1,熟练掌握在乘法算式中,积与因数大小关系的判断。
18.12;;;;
;4;;;
;
【详解】略
19.144千克
【分析】由图形可知,单位“1”是总的千克数,是240千克,求它的是多少,用乘法计算即可解答。
【详解】240×=144(千克)
20.80千米
【分析】由图形可知,单位“1”是总的千米数,是200千米,求它的几分之几是多少,用乘法计算。先求出单位“1”的,再求出剩下部分的,即可解答。
【详解】200××(1-)
=100×
=80(千米)
21.21;1;
【分析】,根据乘法分配律,将算式变为进行简算即可;
,根据加法交换律和减法的性质,将算式变为)进行简算即可;
,先计算出乘法,再计算出加法。
【详解】
)
22.千克
【分析】把小麦的质量看作单位“1”,根据分数乘法的意义,用小麦的质量乘,即可计算出千克这样的小麦,含有淀粉多少千克。
【详解】×=(千克)
答:有千克这样的小麦,含有淀粉千克。
【点睛】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
23.
【分析】把这块试验田的总面积看作单位“1”,是山羊种植的面积所占总面积的分率,已知绵羊种植的面积是山羊种植面积的,用乘即绵羊种植的面积所占总面积的分率。
【详解】×
答:绵羊种的新草占这块试验田的。
【点睛】本题考查了学生完成简单的分数乘法应用题的能力。
24.当天的水果卖完了,原因见详解。
【分析】把水果总量看作单位“1”,先求出下午卖的水果重量占全部的分率,再加上午卖了水果总量的分率,与“1”比较即可。
【详解】
=
=
答:当天的水果卖完了。下午卖的水果相当于水果总量的,加上上午卖的水果总量的,正好是全部水果量。
【点睛】本题主要考查了分数四则复合应用题,解题的关键是求出上午和下午卖的分率和。
25.;图见详解
【分析】把长方形看作单位“1”,平均分成6份,取其中的5份涂色,再把涂色部分看作单位“1”,平均分成4份,取其中的1份涂色,即表示×,据此解答。
【详解】×=
【点睛】本题主要考查两个分数相乘的意义,通过画图可以更直观的了解。
26.(1)是全程的;
(2)最后10分钟走得最快,见详解
【分析】(1)把全程看作单位“1”,全程分成3段,第一段占全程的,第二段占剩下的,最后10分钟占剩下的,用1-即剩下的占全程的分率,再乘即最后10分钟走的路程是全程的几分之几。
(2)先依据速度=路程÷时间,分别求出三种情况下的速度,再根据分数大小比较方法即可解答。
【详解】(1)(1-)×
=×
=
答:最后10分钟走的路程是全程的。
(2)÷25
=×
=
÷20
=×
=
÷10
=×
=
<<
前25分钟平均每分钟行驶总路程的,中间20分钟平均每分钟行驶总路程的,最后10分钟平均每分钟行驶总路程的,最后10分钟走得快。
答:最后10分钟走得最快;同分子分数比较大小时,分子相同时,分母小的分数大。
【点睛】此题的解题关键是确定单位“1”,利用分数加减法的意义求出结果。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
