第五章生活中的轴对称同步练习 北师大版数学七年级下册(无答案)
文档属性
| 名称 | 第五章生活中的轴对称同步练习 北师大版数学七年级下册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1006.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 13:53:58 | ||
图片预览


文档简介
第五章生活中的轴对称
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图①是长方形纸带,,将纸带沿EF折叠成图②,再沿GE折叠成图③,则图③中的度数是( )
A. B. C. D.
2.下面4个图案中是轴对称图形的是( )
A. B.
C. D.
3.如图所示,将一张长方形纸片斜折过去,使顶点A落在处,为折痕,然后再把折过去,使之与重合,折痕为,若,则求的度数( )
A.29° B.32° C.34° D.56°
4.将一条两边沿互相平行的纸带按如图折叠,当∠1:∠2=2:3,则∠2的度数为( )
A.22.50 B.450 C.67.50 D.300
5.数学课上,小明用尺规在黑板上作∠AOB的平分线,并进行简单的说理,下面是小明的解答过程,则符号“ 、 、☆、 ”代表的内容错误的是( )
已知:∠AOB. 求作:射线OC,使∠AOC=∠BOC. 作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使 ; (2)分别以点D,E为圆心、以 为半径作弧,两弧在∠AOB内交于点C; (3)作射线OC.OC就是∠AOB的平分线. 理由: (1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由☆; (2)所以∠AOC=∠BOC,理由 .
A. 表示“OD=OE” B. 表示“大于DE的长”
C.☆表示“SAS” D. 表示“全等三角形的对应角相等”
6.下列四个图形分别是四届国际数学家大会的会标,其中是轴对称图形的是( )
A. B. C. D.
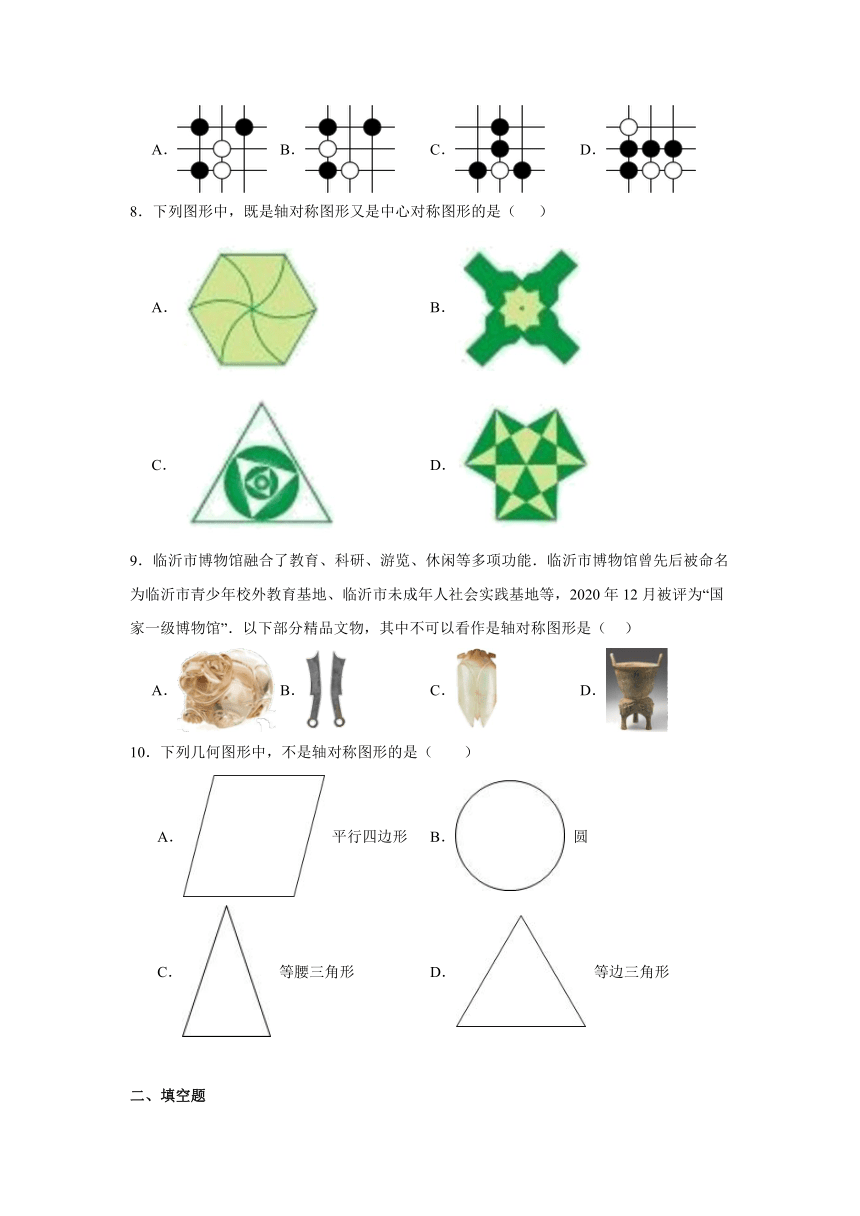
7.围棋起源于中国,古代称之为“亦”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是轴对称图形的是( )
A. B. C. D.
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
9.临沂市博物馆融合了教育、科研、游览、休闲等多项功能.临沂市博物馆曾先后被命名为临沂市青少年校外教育基地、临沂市未成年人社会实践基地等,2020年12月被评为“国家一级博物馆”.以下部分精品文物,其中不可以看作是轴对称图形是( )
A. B. C. D.
10.下列几何图形中,不是轴对称图形的是( )
A. 平行四边形 B. 圆
C. 等腰三角形 D. 等边三角形
二、填空题
11.如图,的面积为24,的长为8,平分,E、F分别是和上的动点,则的最小值为 .
12.如图,在中,,平分交于D,点E,F分别是上的点.将沿折叠,点B恰好与点D重合,若四边形的周长为16,则的长为 .
13.如图,是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在从剩余的13个白色小正方形中选出一个涂成黑色,使涂成黑色的四个小正方形所构成的图形是轴对称图形,则这样的白色小正方形有 个.
14.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1=
15.如图,AD是三角形ABC的对称轴,点E、F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是 .
16.如图,将一张纸条折叠,若∠1=62°,则∠2的度数为 .
17.如图,在的正方形网格中,每个小正方形的边长为1,点M、N、P均为格点(格点是指每个小正方形的顶点),在图中过P点画线段(A、B是格点),当时(不和重合),线段共有 条.
18.把一张长方形纸按图所示折叠后,如果∠AOB′=20°,那么∠BOG的度数是 .
19.如图,将一张长方形纸斜折过去,使顶点落在处,为折痕,然后把折过去,使之落在所在直线上,折痕为,那么两折痕与间的夹角是 °.
20.如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为 °.
三、解答题
21.在3×3的正方形格点图中,和是关于某条直线成轴对称的两个格点三角形(三角形顶点都是小正方形顶点),现给出了,在下面的图中画出4个符合条件的.
22.如图所示为一张直角三角形纸片,将直角边AC沿直线AD折叠,使它与AE重合,点E为AB的中点,求证:△BDE≌△ADC.
23.在棋盘中建立如图所示的平面直角坐标系,其中处各有一颗棋子.
(1)如图1,依次连接A,B,C,A,得到一个等腰三角形(BC为底边),请在图中画出该图形的对称轴.
(2)如图2,现x轴上有两颗棋子P,Q,且(P在Q的左边),依次连接A,P,Q,B,使得 的长度最短,请在图2中标出棋子P,Q的位置,并写出P,Q的坐标.
24.如图与关于直线对称,与的交点F在直线上若,
(1)求的长度;
(2)求的度数.
25.如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在y轴上画出点P,使PA+PC最小;
(4)求六边形AA1C1B1BC的面积..
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图①是长方形纸带,,将纸带沿EF折叠成图②,再沿GE折叠成图③,则图③中的度数是( )
A. B. C. D.
2.下面4个图案中是轴对称图形的是( )
A. B.
C. D.
3.如图所示,将一张长方形纸片斜折过去,使顶点A落在处,为折痕,然后再把折过去,使之与重合,折痕为,若,则求的度数( )
A.29° B.32° C.34° D.56°
4.将一条两边沿互相平行的纸带按如图折叠,当∠1:∠2=2:3,则∠2的度数为( )
A.22.50 B.450 C.67.50 D.300
5.数学课上,小明用尺规在黑板上作∠AOB的平分线,并进行简单的说理,下面是小明的解答过程,则符号“ 、 、☆、 ”代表的内容错误的是( )
已知:∠AOB. 求作:射线OC,使∠AOC=∠BOC. 作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使 ; (2)分别以点D,E为圆心、以 为半径作弧,两弧在∠AOB内交于点C; (3)作射线OC.OC就是∠AOB的平分线. 理由: (1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由☆; (2)所以∠AOC=∠BOC,理由 .
A. 表示“OD=OE” B. 表示“大于DE的长”
C.☆表示“SAS” D. 表示“全等三角形的对应角相等”
6.下列四个图形分别是四届国际数学家大会的会标,其中是轴对称图形的是( )
A. B. C. D.
7.围棋起源于中国,古代称之为“亦”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是轴对称图形的是( )
A. B. C. D.
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
9.临沂市博物馆融合了教育、科研、游览、休闲等多项功能.临沂市博物馆曾先后被命名为临沂市青少年校外教育基地、临沂市未成年人社会实践基地等,2020年12月被评为“国家一级博物馆”.以下部分精品文物,其中不可以看作是轴对称图形是( )
A. B. C. D.
10.下列几何图形中,不是轴对称图形的是( )
A. 平行四边形 B. 圆
C. 等腰三角形 D. 等边三角形
二、填空题
11.如图,的面积为24,的长为8,平分,E、F分别是和上的动点,则的最小值为 .
12.如图,在中,,平分交于D,点E,F分别是上的点.将沿折叠,点B恰好与点D重合,若四边形的周长为16,则的长为 .
13.如图,是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在从剩余的13个白色小正方形中选出一个涂成黑色,使涂成黑色的四个小正方形所构成的图形是轴对称图形,则这样的白色小正方形有 个.
14.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1=
15.如图,AD是三角形ABC的对称轴,点E、F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是 .
16.如图,将一张纸条折叠,若∠1=62°,则∠2的度数为 .
17.如图,在的正方形网格中,每个小正方形的边长为1,点M、N、P均为格点(格点是指每个小正方形的顶点),在图中过P点画线段(A、B是格点),当时(不和重合),线段共有 条.
18.把一张长方形纸按图所示折叠后,如果∠AOB′=20°,那么∠BOG的度数是 .
19.如图,将一张长方形纸斜折过去,使顶点落在处,为折痕,然后把折过去,使之落在所在直线上,折痕为,那么两折痕与间的夹角是 °.
20.如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为 °.
三、解答题
21.在3×3的正方形格点图中,和是关于某条直线成轴对称的两个格点三角形(三角形顶点都是小正方形顶点),现给出了,在下面的图中画出4个符合条件的.
22.如图所示为一张直角三角形纸片,将直角边AC沿直线AD折叠,使它与AE重合,点E为AB的中点,求证:△BDE≌△ADC.
23.在棋盘中建立如图所示的平面直角坐标系,其中处各有一颗棋子.
(1)如图1,依次连接A,B,C,A,得到一个等腰三角形(BC为底边),请在图中画出该图形的对称轴.
(2)如图2,现x轴上有两颗棋子P,Q,且(P在Q的左边),依次连接A,P,Q,B,使得 的长度最短,请在图2中标出棋子P,Q的位置,并写出P,Q的坐标.
24.如图与关于直线对称,与的交点F在直线上若,
(1)求的长度;
(2)求的度数.
25.如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在y轴上画出点P,使PA+PC最小;
(4)求六边形AA1C1B1BC的面积..
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
