广西省试题汇编-03圆柱与圆锥(经典常考题)-小学六年级数学下册(人教版)(含解析)
文档属性
| 名称 | 广西省试题汇编-03圆柱与圆锥(经典常考题)-小学六年级数学下册(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 364.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 15:41:12 | ||
图片预览



文档简介
广西省试题汇编-03圆柱与圆锥(经典常考题)-小学六年级数学下册(人教版)
一、选择题
1.(22-23六年级下·广西南宁·期末)小明把刚买的一支圆柱形铅笔削尖,笔尖(圆锥部分)的体积是铅笔削去部分体积的( )。
A. B.3倍 C. D.
2.(22-23六年级下·广西南宁·期末)“等积变形”的数学思想方法是指图形或物体的形状改变,但是面积或体积不变。下面运用了“等积变形”这一思想方法的有( )。
A.①③ B.①②③ C.①②③④ D.④
3.(21-22六年级下·广西玉林·期末)等底等高的圆柱、正方体、长方体和圆锥相比较,( )的体积最小。
A.圆柱 B.圆锥 C.正方体
4.(20-21六年级下·广西玉林·期末)我们在探究圆柱体积公式时,运用的方法是( )。
A.转化 B.旋转 C.倒推
5.(20-21六年级下·广西钦州·期末)一个圆柱体和一个圆锥体的底面积和高都相等,这个圆柱体和圆锥体的体积比是( )。
A.1∶3 B.3∶1 C.3∶2
二、填空题
6.(22-23六年级下·广西南宁·期末)如图是一个长方形,如在这个长方形中剪下一个最大的正方形,并以正方形的一条边为轴快速旋转一周后会形成一个( )体,它的体积是( )立方厘米。
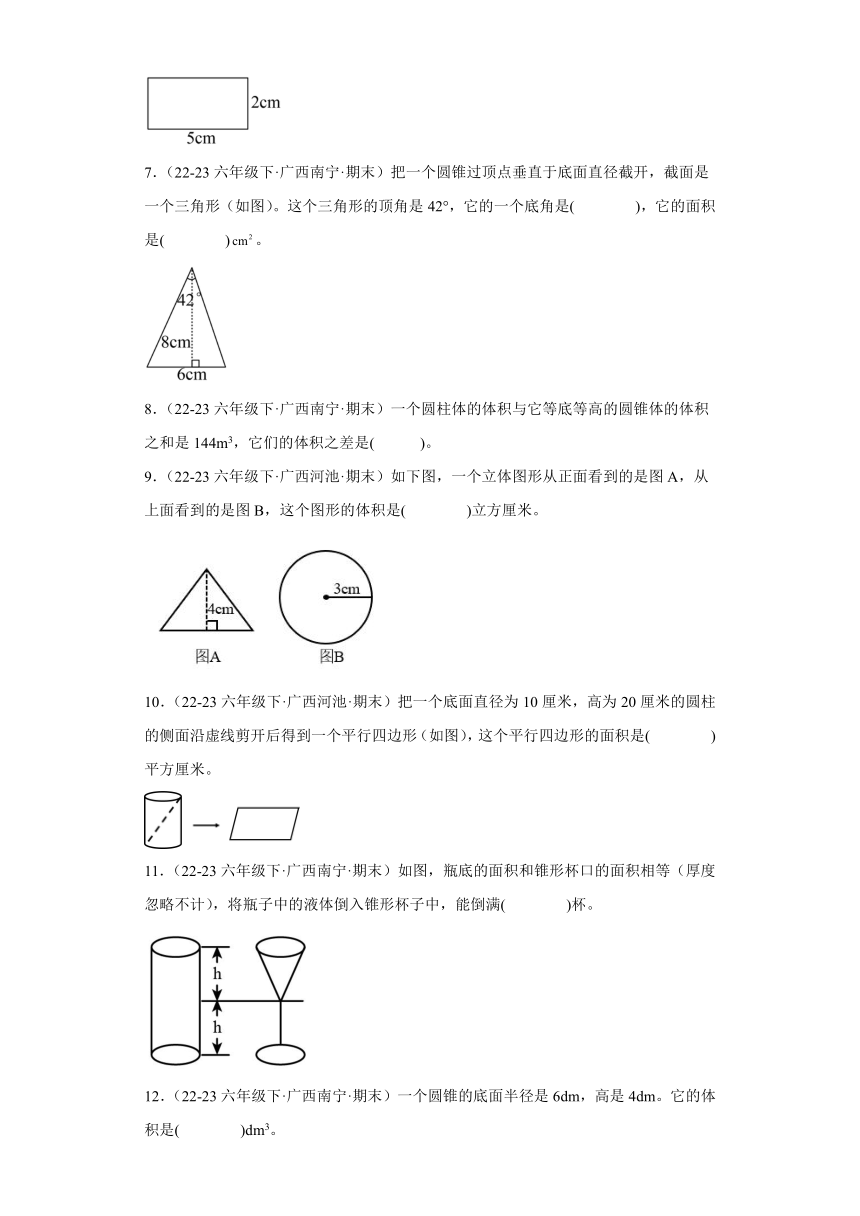
7.(22-23六年级下·广西南宁·期末)把一个圆锥过顶点垂直于底面直径截开,截面是一个三角形(如图)。这个三角形的顶角是42°,它的一个底角是( ),它的面积是( )。
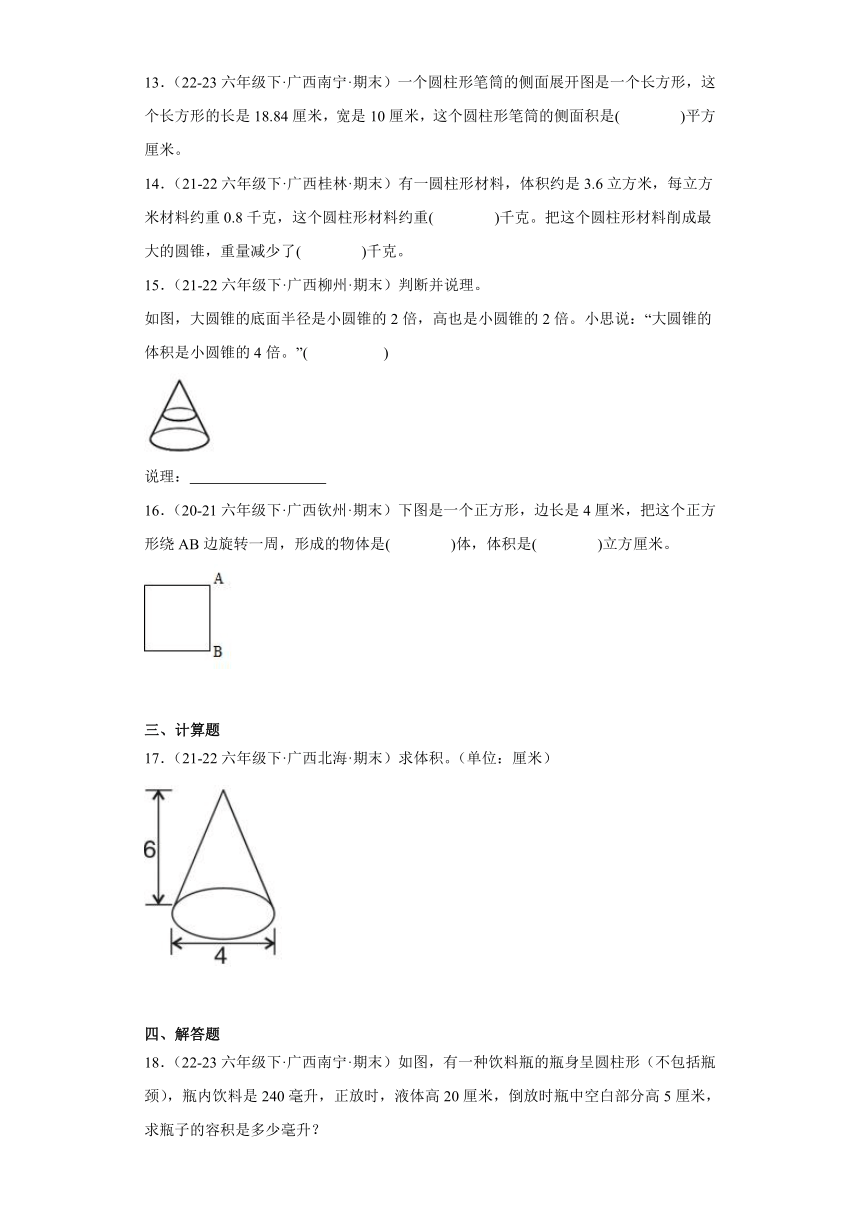
8.(22-23六年级下·广西南宁·期末)一个圆柱体的体积与它等底等高的圆锥体的体积之和是144m3,它们的体积之差是( )。
9.(22-23六年级下·广西河池·期末)如下图,一个立体图形从正面看到的是图A,从上面看到的是图B,这个图形的体积是( )立方厘米。
10.(22-23六年级下·广西河池·期末)把一个底面直径为10厘米,高为20厘米的圆柱的侧面沿虚线剪开后得到一个平行四边形(如图),这个平行四边形的面积是( )平方厘米。
11.(22-23六年级下·广西南宁·期末)如图,瓶底的面积和锥形杯口的面积相等(厚度忽略不计),将瓶子中的液体倒入锥形杯子中,能倒满( )杯。
12.(22-23六年级下·广西南宁·期末)一个圆锥的底面半径是6dm,高是4dm。它的体积是( )dm3。
13.(22-23六年级下·广西南宁·期末)一个圆柱形笔筒的侧面展开图是一个长方形,这个长方形的长是18.84厘米,宽是10厘米,这个圆柱形笔筒的侧面积是( )平方厘米。
14.(21-22六年级下·广西桂林·期末)有一圆柱形材料,体积约是3.6立方米,每立方米材料约重0.8千克,这个圆柱形材料约重( )千克。把这个圆柱形材料削成最大的圆锥,重量减少了( )千克。
15.(21-22六年级下·广西柳州·期末)判断并说理。
如图,大圆锥的底面半径是小圆锥的2倍,高也是小圆锥的2倍。小思说:“大圆锥的体积是小圆锥的4倍。”( )
说理:
16.(20-21六年级下·广西钦州·期末)下图是一个正方形,边长是4厘米,把这个正方形绕AB边旋转一周,形成的物体是( )体,体积是( )立方厘米。
三、计算题
17.(21-22六年级下·广西北海·期末)求体积。(单位:厘米)
四、解答题
18.(22-23六年级下·广西南宁·期末)如图,有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),瓶内饮料是240毫升,正放时,液体高20厘米,倒放时瓶中空白部分高5厘米,求瓶子的容积是多少毫升?
19.(22-23六年级下·广西南宁·期末)把一个长、宽、高分别是8厘米、4厘米、3厘米的长方体铁块和一个棱长为4厘米的正方体铁块熔铸成一个圆锥体。这个圆锥体的底面积是1.2平方分米,高是多少?
20.(22-23六年级下·广西河池·期末)如图,一个底面内直径为2厘米,高为7厘米的瓶子,里面水的高度是4厘米,把瓶盖拧紧,倒置放平后,水的高度为5厘米,请你计算瓶子的容积是多少立方厘米?
21.(22-23六年级下·广西南宁·期末)如图,将圆柱切拼成近似的长方体后,长方体右侧面积为15平方厘米,原来圆柱的表面积是多少平方厘米?
22.(22-23六年级下·广西南宁·期末)一种由圆柱和圆锥组成的存储粮食的漏斗形粮仓(如图,单位:米),这个漏斗形粮仓最多能存储粮食多少立方米?
23.(22-23六年级下·广西河池·期末)乡村振兴工作队要在和平村修建一个圆柱体沼气池。底面直径是4米,深2米,要在沼气池的侧面与下底面抹上水泥。抹水泥部分的面积是多少平方米?
24.(21-22六年级下·广西北海·期末)妈妈的茶杯,这样放在桌子上。(如下图)
(1)这只茶杯占据桌面的大小是多少平方厘米?
(2)这只茶杯装满水后的体积是多少?
25.(21-22六年级下·广西南宁·期末)一个正方体玻璃鱼缸从内测量棱长是5分米,水深3分米。李明现在将一个底面积是12.5平方分米的圆锥装饰物放入鱼缸,完全浸没在水中,这时水面上升了2厘米,这个圆锥装饰物的高是多少?
26.(21-22六年级下·广西玉林·期末)陀螺在我国最少有四、五千年的历史,是民间最早的娱乐工具之一。小刚有一个底面直径是6厘米的木制陀螺(如图),这个陀螺的体积是多少立方厘米?
27.(21-22六年级下·广西桂林·期末)一个圆锥形沙堆,底面半径是0.9米,高是1.5米。将这些沙子均匀铺在一个长3米,宽1.5米,深0.5米的长方体沙坑里,能铺多厚?(π取3.14)
28.(20-21六年级下·广西柳州·期末)如下图,两个完全一样的杯子,装有同样多的水,分别放入等底等高的圆柱与圆锥零件后,水面的高度都上升了,水未溢出。A杯的水面上升了2厘米。
(1)B杯的水面上升了( )厘米。
(2)圆锥零件的体积是多少立方厘米?
29.(21-22六年级下·广西柳州·期末)每天早晨,小维妈妈都要给家人榨新鲜果汁。
(1)榨出的果汁用圆柱形容器装(如下图),正好装满,榨出的果汁有多少毫升?(容器的厚度忽略不计)
(2)如果用底面积是25cm2、高是10cm的近似长方体方口玻璃杯装,够小维家5口人每人一满杯吗?(容器的厚度忽略不计)
30.(20-21六年级下·广西玉林·期末)两个大小相同的圆柱形量杯中,都盛有500毫升水,将高和底面积都相等的圆柱与圆锥零件分别浸放在水中,乙量杯水面刻度如图所示,圆锥零件体积是多少立方厘米?甲量杯水面刻度应是多少毫升?
参考答案:
1.D
【分析】把圆柱的体积看作单位“1”,当圆柱与圆锥等底等高时,圆锥的体积是圆柱体积的,则削去部分的体积占圆柱体积的(1-),最后用除法求出笔尖的体积占削去部分体积的分率,据此解答。
【详解】÷(1-)
=÷
=×
=
则笔尖(圆锥部分)的体积是笔芯削去部分体积的。
故答案为:D
2.B
【分析】①观察图形可知,利用排水法求正方体木块的体积,即将正方体木块的体积转化为圆柱的体积,形状改变,但体积不变,符合等积变形这一思想方法;
②将两个不规则图形合并长方形,进而根据长方形的面积的计算方法求得两个不规则图形的面积之和,形状改变,但面积不变,符合等积变形这一思想方法;
③将圆锥沙堆转化为长方体沙堆,形状虽改变,但体积不变,符合等积变形这一思想方法;
④求阴影部分的面积,用圆的面积减去中间正方形的面积即可,阴影部分的形状没有发生变化,不符合等积变形这一思想方法。
【详解】由分析可知:
运用了“等积变形”这一思想方法的有①②③。
故答案为:B
3.B
【分析】圆柱、圆锥、正方体、长方体,它们的体积都可以转化成我们学过的“底面积×高”来解决;再结合等底等高的圆锥的体积是圆柱的,可得在等底等高的圆柱、正方体、长方体和圆锥相比较,圆锥的体积最小。
【详解】根据直柱体体积公式及等底等高圆锥体积与圆柱体积的关系可得:
等底等高的圆柱、正方体、长方体和圆锥相比较,(圆锥)的体积最小。
故答案为:B
【点睛】熟悉体积公式“底面积×高”的意义,且能够明确求哪些物体的体积可以使用这个公式,是解题关键。
4.A
【分析】我们在探究圆柱体积公式时,是把圆柱沿底面半径切割成若干等份后,拼组成长方体,利用长方体的体积公式推导圆柱的体积公式的过程,据此解答。
【详解】根据分析可知,圆柱切割成近似长方体,近似长方体的底面积等于圆柱的底面积,近似长方体的高等于圆柱的高,由此圆柱的体积=底面积×高,这个过程体现了转化的数学思想。
故答案为:A
【点睛】解答本题的关键明确利用长方体的体积公式推导出圆柱体积公式的方法。
5.B
【分析】底面积和高都相等的圆柱和圆锥,圆柱的体积是圆锥的3倍,如果圆锥的体积为1份数,那么圆柱的体积就为3份数,进而写出比即可。
【详解】因为等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍,
所以圆柱和圆锥的体积比为:3∶1。
故答案为:B
【点睛】此题考查比的意义和等底等高的条件下圆柱和圆锥的关系。
6. 圆柱 25.12
【分析】在这个长方形中剪下一个最大的正方形,则该正方形的边长相当于长方形的宽,即2厘米;以正方形的一条边为轴快速旋转一周后会形成一个底面半径为2厘米,高为2厘米的圆柱,再根据圆柱的体积公式:V=πr2h,据此计算即可。
【详解】由分析可知:
以正方形的一条边为轴快速旋转一周后会形成一个圆柱体。
3.14×22×2
=3.14×4×2
=12.56×2
=25.12(立方厘米)
则它的体积是25.12立方厘米。
7. 69°/69度 24
【分析】圆锥沿高截开后截面是一个等腰三角形,等腰三角形的两个底角相等,根据三角形的内角和是180°求出等腰三角形的一个底角;再根据三角形的面积=底×高÷2,代入数据解答即可。
【详解】(180°-42°)÷2
=138°÷2
=69°
8×6÷2
=48÷2
=24(cm2)
它的一个底角是69°,它的面积是24。
8.72m3
【分析】根据等底等高的圆柱体的体积等于圆锥体的体积的3倍,据此解答即可。
【详解】据题意可知:
V圆柱=3V圆锥
V圆柱+V圆锥=144
V圆锥=144÷(3+1)
=144÷4
=36(m3)
V圆柱=36×3=108(m3)
所以,它们的体积之差是:108-36=72(m3)
【点睛】本题考查圆柱体的体积和圆锥体的体积之间的关系,关键要抓住等底等高这个条件。
9.37.68
【分析】观察这个图形可以发现是圆锥,圆锥的高是4厘米,底面半径是3厘米,根据圆锥的体积公式进行解答即可。
【详解】
(立方厘米)
所以这个图形的体积是37.68立方厘米。
【点睛】本题考查圆锥的体积,解答本题的关键是掌握圆锥的体积公式。
10.628
【分析】由图可知,剪开之后平行四边形的面积等于原来圆柱的侧面积,利用“”求出这个平行四边形的面积,据此解答。
【详解】3.14×10×20
=31.4×20
=628(平方厘米)
所以,这个平行四边形的面积是628平方厘米。
【点睛】本题主要考查圆柱的侧面积,熟记公式是解答题目的关键。
11.6
【分析】由图可知,圆柱的底面积和圆锥的底面积相等,把瓶子中的液体看作一个圆柱, 圆柱的一半与圆锥等底等高,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,液体的一半倒入锥形杯子中可以倒3杯,那么全部液体可以倒6杯,据此解答。
【详解】由分析可知:
把瓶内液体的体积看作与锥形杯子等底等高的两部分,一部分倒入锥形杯子中可以倒3杯。
3×2=6(杯)
则将瓶子中的液体倒入锥形杯子中,能倒满6杯。
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
12.150.72
【分析】已知圆锥的底面半径和高,根据圆锥的体积公式V=πr2h,代入数据计算,即可求出它的体积。
【详解】×3.14×62×4
=×3.14×36×4
=150.72(dm3)
它的体积是150.72dm3。
【点睛】本题考查圆锥体积公式的运用。
13.188.4
【分析】这个圆柱形笔筒的侧面展开图是一个长方形,则圆柱的侧面积等于长方形的面积,利用“长方形的面积=长×宽”求出这个笔筒的侧面积,据此解答。
【详解】18.84×10=188.4(平方厘米)
所以,这个圆柱形笔筒的侧面积是188.4平方厘米。
【点睛】本题主要考查圆柱的侧面积,理解长方形的面积等于圆柱的侧面积是解答题目的关键。
14. 2.88 1.92
【分析】用圆柱的体积乘每立方米材料的重量,即可求出这个圆柱形材料的重量;圆柱内最大的圆锥与原来圆柱是等底等高的,所以圆锥的体积是圆柱的体积的,则削去部分的体积是圆柱体积的(1-),据此求出减少部分的体积,再乘每立方米材料的重量,即可解答。
【详解】3.6×0.8=2.88(千克)
3.6×(1-)×0.8
=3.6××0.8
=2.4×0.8
=1.92(千克)
【点睛】抓住圆柱内最大圆锥的特点以及等底等高的圆柱的体积与圆锥的体积的倍数关系即可解决此类问题。
15. × 大圆锥的底面半径是小圆锥的2倍,则大圆锥的底面积是小圆锥底面积的4倍,高也是小圆锥的2倍,则大圆锥的体积是小圆锥体积的8倍。
【分析】根据圆锥的体积公式:V=,再根据因数与积的变化规律,积扩大倍数等于两个因数扩大倍数的乘积,据此判断即可。
【详解】根据圆的面积可知,若大圆锥的底面半径是小圆锥的2倍,则大圆锥的底面积是小圆锥底面积的4倍;同时大圆锥的高也是小圆锥高的2倍,根据圆锥的体积公式可知,则大圆锥的体积是小圆锥体积的8倍。即2×2×2=8。
所以要判定题干中的说法为:×
理由:大圆锥的底面半径是小圆锥的2倍,则大圆锥的底面积是小圆锥底面积的4倍,高也是小圆锥的2倍,则大圆锥的体积是小圆锥体积的8倍。
【点睛】此题主要考查圆锥的体积公式的灵活运用以及因数与积的变化规律,关键是熟记公式。
16. 圆柱 200.96
【分析】正方形的边长是4厘米,绕着这个正方形的一边旋转一周,得到的几何体是圆柱体。圆柱的高和半径相等,都是4厘米,利用圆柱的体积公式:,代入数据求出圆柱的体积。
【详解】上图是一个正方形,边长是4厘米,把这个正方形绕AB边旋转一周,形成的物体是圆柱体。
3.14×42×4
=3.14×16×4
=200.96(立方厘米)
【点睛】此题主要考查圆柱的特征以及灵活运用圆柱的体积公式。
17.25.12立方厘米
【分析】由图可知,圆锥的底面直径是4厘米,高是6厘米,利用“”求出圆锥的体积,据此解答。
【详解】×3.14×(4÷2)2×6
=×3.14×4×6
=×6×3.14×4
=(×6)×(3.14×4)
=2×12.56
=25.12(立方厘米)
所以,圆锥的体积是25.12立方厘米。
18.300毫升
【分析】根据圆柱的容积公式:容积=底面积×高;底面积=容积÷高,用瓶内饮料的容积除以此时的高度,即240÷20,求出这个饮料瓶底的底面积;空白处的容积等于底面积是圆柱形饮料瓶的底面积,高是5厘米的圆柱的容积,代入数据,求出空白处的容积,再加上瓶内饮料的容积,注意单位名数的换算;即可解答。
【详解】240毫升=240立方厘米
240÷20=12(平方厘米)
12×5=60(立方厘米)
60立方厘米=60毫升
60+240=300(毫升)
答:瓶子的容积是300毫升。
19.4厘米
【分析】由题意可知:圆锥的体积等于长方体铁块与正方体铁块的体积和。先根据“长方体的体积=长×宽×高”求出长方体铁块的体积;再根据“正方体的体积=棱长×棱长×棱长”求出正方体铁块的体积;再用长方体铁块的体积加上正方体铁块的体积求出圆锥的体积;最后根据“圆锥的高=圆锥的体积÷÷底面积”求出圆锥的高。
【详解】1.2平方分米=120平方厘米
8×4×3+4×4×4
=96+64
=160(立方厘米)
160÷÷120
=160×3÷120
=480÷120
=4(厘米)
答:高是4厘米。
【点睛】此题考查了长方体、正方体、圆锥的体积计算公式。解决此题关键是明确熔铸前后铁块的形状发生了变化,但体积不变。
20.18.84立方厘米
【分析】瓶子的容积=水的体积+空白部分的容积,倒置放平后,空白部分是个高(7-5)厘米的圆柱,根据圆柱体积=底面积×高,分别求出水的体积和空白部分的容积,相加即可。
【详解】3.14×(2÷2)2×4+3.14×(2÷2)2×(7-5)
=3.14×12×4+3.14×12×2
=3.14×1×4+3.14×1×2
=12.56+6.28
=18.84(立方厘米)
答:瓶子的容积是18.84立方厘米。
【点睛】关键是利用转化思想,将不规则部分的容积转化为圆柱进行计算。
21.150.72平方厘米
【分析】根据题意,把圆柱切拼成近似长方体,那么这个长方体的长等于圆柱底面周长的一半,长方体的宽等于圆柱的底面半径,长方体的高等于圆柱的高;
已知长方体右侧面积为15平方厘米,即已知长方体右面“宽×高”的积,用右侧面积除以高,即可求出长方体的宽,也是圆柱的底面半径;
再根据圆柱的表面积S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算即可。
【详解】圆柱的底面半径:
15÷5=3(厘米)
圆柱的表面积:
2×3.14×3×5+3.14×32×2
=3.14×30+3.14×9×2
=94.2+56.52
=150.72(平方厘米)
答:原来圆柱的表面积是150.72平方厘米。
【点睛】本题考查圆柱表面积公式的运用,掌握圆柱体积公式的推导过程,理解拼成的近似长方体和圆柱之间的联系,求出圆柱的底面半径是解题的关键。
22.62.8立方米
【分析】观察图形可知,图形的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算,即可求出这个粮仓最多能存储粮食的体积。
【详解】圆柱的体积:
3.14×(4÷2)2×4
=3.14×4×4
=50.24(立方米)
圆锥的体积:
×3.14×(4÷2)2×(7-4)
=×3.14×4×3
=12.56(立方米)
一共:50.24+12.56=62.8(立方米)
答:这个漏斗形粮仓最多能存储粮食62.8立方米。
【点睛】本题考查圆柱、圆锥体积公式的运用,结合图形,分析出组合体的体积是由哪些立体图形的体积相加或相减得到,再利用图形的体积公式列式计算。
23.37.68平方米
【分析】由题意可知,计算抹水泥部分的面积就是求圆柱的侧面积与一个底面积的和,利用“”求出需要抹水泥部分的面积,据此解答。
【详解】3.14×4×2+3.14×(4÷2)2
=3.14×4×2+3.14×4
=12.56×2+12.56
=25.12+12.56
=37.68(平方米)
答:抹水泥部分的面积是37.68平方米。
【点睛】本题主要考查圆柱表面积公式的应用,明确需要计算圆柱哪些面的面积是解答题目的关键。
24.(1)28.26平方厘米;
(2)423.9立方厘米
【分析】(1)求茶杯占据桌面的大小就是求圆柱的底面积,利用“”求出茶杯的底面积;
(2)求茶杯装满水后的体积就是求圆柱的体积,利用“”求出茶杯的体积,据此解答。
【详解】(1)3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
答:这只茶杯占据桌面的大小是28.26平方厘米。
(2)28.26×15=423.9(立方厘米)
答:这只茶杯装满水后的体积是423.9立方厘米。
【点睛】掌握圆的面积和圆柱的体积计算公式是解答题目的关键。
25.1.2分米
【分析】圆锥装饰物放入鱼缸后,先换算单位,水面上升的高度为0.2分米,圆锥装饰物的体积等于水面上升的体积,水面上升的体积可看作长宽均为5分米,高为0.2分米的长方体的体积,根据长方体的体积公式:V=abh,代入数据即可求出这个圆锥装饰物的体积,再利用圆锥的体积公式:V=Sh,用圆锥装饰物的体积除以圆锥的底面积,即可求出这个圆锥装饰物的高。
【详解】2厘米=0.2分米
5×5×0.2÷÷12.5
=5÷÷12.5
=15÷12.5
=1.2(分米)
答:这个圆锥装饰物的高是1.2分米。
【点睛】此题的解题关键是掌握求不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积和圆锥的体积公式求解。
26.113.04立方厘米
【分析】由题干可知,圆柱和圆锥是等底的,求圆柱和圆锥的体积之和就是陀螺的体积。分别利用圆柱和圆锥的体积公式求解即可。
【详解】3.14×(6÷2)2×3+×3.14×(6÷2)2×3
=3.14×32×3+×3×3.14×32
=3.14×9×3+3.14×9
=84.78+28.26
=113.04(立方厘米)
答:这个陀螺的体积是113.04立方厘米。
【点睛】此题考查的是圆柱和圆锥的体积公式的应用,熟记公式是解题关键。
27.0.2826米
【分析】由题意可知,沙堆的体积是一定的,根据圆锥的体积=×底面积×高,求出圆锥形沙堆的体积,再根据长方体的体积=长×宽×高,求出高即沙的厚度。
【详解】×3.14×0.92×1.5÷(3×1.5)
=×3.14×0.81×1.5÷4.5
=×2.5434×1.5÷4.5
=×3.8151÷4.5
=1.2717÷4.5
=0.2826(米)
答:能铺0.2826米厚。
【点睛】本题考查圆锥和长方体的体积,熟记圆锥和长方体的体积公式是解题的关键。
28.(1)6
(2)56.52立方厘米
【分析】(1)根据等底等高的圆柱的体积是圆锥体积的3倍,两个杯子是完全一样的,A杯的水面上升了2厘米,则B杯的水面上升了(2×3)厘米;(2)圆锥的体积即上升的2厘米水的体积,根据圆柱的体积,据此解答。
【详解】(1)2×3=6(厘米)
(2)
(立方厘米)
答:圆锥零件的体积是56.52立方厘米。
【点睛】灵活掌握圆柱的体积计算公式是解答本题的关键,涉及到的知识点是等底等高的圆柱的体积是圆锥体积的3倍。
29.(1)1130.4mL;
(2)不够
【分析】(1)根据圆柱的容积(体积)公式:,把数据代入公式解答。
(2)根据长方体的体积(容积)公式:,把数据代入公式求出每个玻璃杯的容积,再求出5杯的容积,然后与圆柱形容器的容积进行比较即可。
【详解】(1)3.14×(12÷2)2×10
=3.14×36×10
=113.04×10
=1130.4(cm2)
1130.4cm2=1130.4mL
答:榨出的果汁有1130.4mL。
(2)25×10×5
=250×5
=1250(mL)
1130.4mL<1250mL
答:不够小维家5口人每人一满杯。
【点睛】此题主要考查圆柱的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
30.立方厘米;毫升
【分析】根据题意可知,圆柱形量杯中,都盛有500毫升的水,加入圆锥形零件后,乙量杯水的容积是600毫升水,把容积换成体积;用加入圆锥形零件后水的体积减去加入圆锥形零件前水的体积,即可求出圆锥形零件的体积;再根据等底等高的圆锥体体积是圆柱体积的,求出圆柱形零件的体积,再加上原来甲量杯中水的体积,就是加入圆柱形零件后水与圆柱形零件的体积,再化成容积,即可求出量杯中水面的刻度。
【详解】500毫升=500立方厘米
600毫升=600立方厘米
圆锥的体积:600-500=100(立方厘米)
圆柱的体积:100×3=300(立方厘米)
300+500=800(立方厘米)
800立方厘米=800毫升
答:圆锥零件的体积是100立方厘米,甲量杯水面刻度是800毫升。
【点睛】解答本题的关键是明确等底等高的圆锥体积是圆柱的;以及单位名数的互换。
一、选择题
1.(22-23六年级下·广西南宁·期末)小明把刚买的一支圆柱形铅笔削尖,笔尖(圆锥部分)的体积是铅笔削去部分体积的( )。
A. B.3倍 C. D.
2.(22-23六年级下·广西南宁·期末)“等积变形”的数学思想方法是指图形或物体的形状改变,但是面积或体积不变。下面运用了“等积变形”这一思想方法的有( )。
A.①③ B.①②③ C.①②③④ D.④
3.(21-22六年级下·广西玉林·期末)等底等高的圆柱、正方体、长方体和圆锥相比较,( )的体积最小。
A.圆柱 B.圆锥 C.正方体
4.(20-21六年级下·广西玉林·期末)我们在探究圆柱体积公式时,运用的方法是( )。
A.转化 B.旋转 C.倒推
5.(20-21六年级下·广西钦州·期末)一个圆柱体和一个圆锥体的底面积和高都相等,这个圆柱体和圆锥体的体积比是( )。
A.1∶3 B.3∶1 C.3∶2
二、填空题
6.(22-23六年级下·广西南宁·期末)如图是一个长方形,如在这个长方形中剪下一个最大的正方形,并以正方形的一条边为轴快速旋转一周后会形成一个( )体,它的体积是( )立方厘米。
7.(22-23六年级下·广西南宁·期末)把一个圆锥过顶点垂直于底面直径截开,截面是一个三角形(如图)。这个三角形的顶角是42°,它的一个底角是( ),它的面积是( )。
8.(22-23六年级下·广西南宁·期末)一个圆柱体的体积与它等底等高的圆锥体的体积之和是144m3,它们的体积之差是( )。
9.(22-23六年级下·广西河池·期末)如下图,一个立体图形从正面看到的是图A,从上面看到的是图B,这个图形的体积是( )立方厘米。
10.(22-23六年级下·广西河池·期末)把一个底面直径为10厘米,高为20厘米的圆柱的侧面沿虚线剪开后得到一个平行四边形(如图),这个平行四边形的面积是( )平方厘米。
11.(22-23六年级下·广西南宁·期末)如图,瓶底的面积和锥形杯口的面积相等(厚度忽略不计),将瓶子中的液体倒入锥形杯子中,能倒满( )杯。
12.(22-23六年级下·广西南宁·期末)一个圆锥的底面半径是6dm,高是4dm。它的体积是( )dm3。
13.(22-23六年级下·广西南宁·期末)一个圆柱形笔筒的侧面展开图是一个长方形,这个长方形的长是18.84厘米,宽是10厘米,这个圆柱形笔筒的侧面积是( )平方厘米。
14.(21-22六年级下·广西桂林·期末)有一圆柱形材料,体积约是3.6立方米,每立方米材料约重0.8千克,这个圆柱形材料约重( )千克。把这个圆柱形材料削成最大的圆锥,重量减少了( )千克。
15.(21-22六年级下·广西柳州·期末)判断并说理。
如图,大圆锥的底面半径是小圆锥的2倍,高也是小圆锥的2倍。小思说:“大圆锥的体积是小圆锥的4倍。”( )
说理:
16.(20-21六年级下·广西钦州·期末)下图是一个正方形,边长是4厘米,把这个正方形绕AB边旋转一周,形成的物体是( )体,体积是( )立方厘米。
三、计算题
17.(21-22六年级下·广西北海·期末)求体积。(单位:厘米)
四、解答题
18.(22-23六年级下·广西南宁·期末)如图,有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),瓶内饮料是240毫升,正放时,液体高20厘米,倒放时瓶中空白部分高5厘米,求瓶子的容积是多少毫升?
19.(22-23六年级下·广西南宁·期末)把一个长、宽、高分别是8厘米、4厘米、3厘米的长方体铁块和一个棱长为4厘米的正方体铁块熔铸成一个圆锥体。这个圆锥体的底面积是1.2平方分米,高是多少?
20.(22-23六年级下·广西河池·期末)如图,一个底面内直径为2厘米,高为7厘米的瓶子,里面水的高度是4厘米,把瓶盖拧紧,倒置放平后,水的高度为5厘米,请你计算瓶子的容积是多少立方厘米?
21.(22-23六年级下·广西南宁·期末)如图,将圆柱切拼成近似的长方体后,长方体右侧面积为15平方厘米,原来圆柱的表面积是多少平方厘米?
22.(22-23六年级下·广西南宁·期末)一种由圆柱和圆锥组成的存储粮食的漏斗形粮仓(如图,单位:米),这个漏斗形粮仓最多能存储粮食多少立方米?
23.(22-23六年级下·广西河池·期末)乡村振兴工作队要在和平村修建一个圆柱体沼气池。底面直径是4米,深2米,要在沼气池的侧面与下底面抹上水泥。抹水泥部分的面积是多少平方米?
24.(21-22六年级下·广西北海·期末)妈妈的茶杯,这样放在桌子上。(如下图)
(1)这只茶杯占据桌面的大小是多少平方厘米?
(2)这只茶杯装满水后的体积是多少?
25.(21-22六年级下·广西南宁·期末)一个正方体玻璃鱼缸从内测量棱长是5分米,水深3分米。李明现在将一个底面积是12.5平方分米的圆锥装饰物放入鱼缸,完全浸没在水中,这时水面上升了2厘米,这个圆锥装饰物的高是多少?
26.(21-22六年级下·广西玉林·期末)陀螺在我国最少有四、五千年的历史,是民间最早的娱乐工具之一。小刚有一个底面直径是6厘米的木制陀螺(如图),这个陀螺的体积是多少立方厘米?
27.(21-22六年级下·广西桂林·期末)一个圆锥形沙堆,底面半径是0.9米,高是1.5米。将这些沙子均匀铺在一个长3米,宽1.5米,深0.5米的长方体沙坑里,能铺多厚?(π取3.14)
28.(20-21六年级下·广西柳州·期末)如下图,两个完全一样的杯子,装有同样多的水,分别放入等底等高的圆柱与圆锥零件后,水面的高度都上升了,水未溢出。A杯的水面上升了2厘米。
(1)B杯的水面上升了( )厘米。
(2)圆锥零件的体积是多少立方厘米?
29.(21-22六年级下·广西柳州·期末)每天早晨,小维妈妈都要给家人榨新鲜果汁。
(1)榨出的果汁用圆柱形容器装(如下图),正好装满,榨出的果汁有多少毫升?(容器的厚度忽略不计)
(2)如果用底面积是25cm2、高是10cm的近似长方体方口玻璃杯装,够小维家5口人每人一满杯吗?(容器的厚度忽略不计)
30.(20-21六年级下·广西玉林·期末)两个大小相同的圆柱形量杯中,都盛有500毫升水,将高和底面积都相等的圆柱与圆锥零件分别浸放在水中,乙量杯水面刻度如图所示,圆锥零件体积是多少立方厘米?甲量杯水面刻度应是多少毫升?
参考答案:
1.D
【分析】把圆柱的体积看作单位“1”,当圆柱与圆锥等底等高时,圆锥的体积是圆柱体积的,则削去部分的体积占圆柱体积的(1-),最后用除法求出笔尖的体积占削去部分体积的分率,据此解答。
【详解】÷(1-)
=÷
=×
=
则笔尖(圆锥部分)的体积是笔芯削去部分体积的。
故答案为:D
2.B
【分析】①观察图形可知,利用排水法求正方体木块的体积,即将正方体木块的体积转化为圆柱的体积,形状改变,但体积不变,符合等积变形这一思想方法;
②将两个不规则图形合并长方形,进而根据长方形的面积的计算方法求得两个不规则图形的面积之和,形状改变,但面积不变,符合等积变形这一思想方法;
③将圆锥沙堆转化为长方体沙堆,形状虽改变,但体积不变,符合等积变形这一思想方法;
④求阴影部分的面积,用圆的面积减去中间正方形的面积即可,阴影部分的形状没有发生变化,不符合等积变形这一思想方法。
【详解】由分析可知:
运用了“等积变形”这一思想方法的有①②③。
故答案为:B
3.B
【分析】圆柱、圆锥、正方体、长方体,它们的体积都可以转化成我们学过的“底面积×高”来解决;再结合等底等高的圆锥的体积是圆柱的,可得在等底等高的圆柱、正方体、长方体和圆锥相比较,圆锥的体积最小。
【详解】根据直柱体体积公式及等底等高圆锥体积与圆柱体积的关系可得:
等底等高的圆柱、正方体、长方体和圆锥相比较,(圆锥)的体积最小。
故答案为:B
【点睛】熟悉体积公式“底面积×高”的意义,且能够明确求哪些物体的体积可以使用这个公式,是解题关键。
4.A
【分析】我们在探究圆柱体积公式时,是把圆柱沿底面半径切割成若干等份后,拼组成长方体,利用长方体的体积公式推导圆柱的体积公式的过程,据此解答。
【详解】根据分析可知,圆柱切割成近似长方体,近似长方体的底面积等于圆柱的底面积,近似长方体的高等于圆柱的高,由此圆柱的体积=底面积×高,这个过程体现了转化的数学思想。
故答案为:A
【点睛】解答本题的关键明确利用长方体的体积公式推导出圆柱体积公式的方法。
5.B
【分析】底面积和高都相等的圆柱和圆锥,圆柱的体积是圆锥的3倍,如果圆锥的体积为1份数,那么圆柱的体积就为3份数,进而写出比即可。
【详解】因为等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍,
所以圆柱和圆锥的体积比为:3∶1。
故答案为:B
【点睛】此题考查比的意义和等底等高的条件下圆柱和圆锥的关系。
6. 圆柱 25.12
【分析】在这个长方形中剪下一个最大的正方形,则该正方形的边长相当于长方形的宽,即2厘米;以正方形的一条边为轴快速旋转一周后会形成一个底面半径为2厘米,高为2厘米的圆柱,再根据圆柱的体积公式:V=πr2h,据此计算即可。
【详解】由分析可知:
以正方形的一条边为轴快速旋转一周后会形成一个圆柱体。
3.14×22×2
=3.14×4×2
=12.56×2
=25.12(立方厘米)
则它的体积是25.12立方厘米。
7. 69°/69度 24
【分析】圆锥沿高截开后截面是一个等腰三角形,等腰三角形的两个底角相等,根据三角形的内角和是180°求出等腰三角形的一个底角;再根据三角形的面积=底×高÷2,代入数据解答即可。
【详解】(180°-42°)÷2
=138°÷2
=69°
8×6÷2
=48÷2
=24(cm2)
它的一个底角是69°,它的面积是24。
8.72m3
【分析】根据等底等高的圆柱体的体积等于圆锥体的体积的3倍,据此解答即可。
【详解】据题意可知:
V圆柱=3V圆锥
V圆柱+V圆锥=144
V圆锥=144÷(3+1)
=144÷4
=36(m3)
V圆柱=36×3=108(m3)
所以,它们的体积之差是:108-36=72(m3)
【点睛】本题考查圆柱体的体积和圆锥体的体积之间的关系,关键要抓住等底等高这个条件。
9.37.68
【分析】观察这个图形可以发现是圆锥,圆锥的高是4厘米,底面半径是3厘米,根据圆锥的体积公式进行解答即可。
【详解】
(立方厘米)
所以这个图形的体积是37.68立方厘米。
【点睛】本题考查圆锥的体积,解答本题的关键是掌握圆锥的体积公式。
10.628
【分析】由图可知,剪开之后平行四边形的面积等于原来圆柱的侧面积,利用“”求出这个平行四边形的面积,据此解答。
【详解】3.14×10×20
=31.4×20
=628(平方厘米)
所以,这个平行四边形的面积是628平方厘米。
【点睛】本题主要考查圆柱的侧面积,熟记公式是解答题目的关键。
11.6
【分析】由图可知,圆柱的底面积和圆锥的底面积相等,把瓶子中的液体看作一个圆柱, 圆柱的一半与圆锥等底等高,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,液体的一半倒入锥形杯子中可以倒3杯,那么全部液体可以倒6杯,据此解答。
【详解】由分析可知:
把瓶内液体的体积看作与锥形杯子等底等高的两部分,一部分倒入锥形杯子中可以倒3杯。
3×2=6(杯)
则将瓶子中的液体倒入锥形杯子中,能倒满6杯。
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
12.150.72
【分析】已知圆锥的底面半径和高,根据圆锥的体积公式V=πr2h,代入数据计算,即可求出它的体积。
【详解】×3.14×62×4
=×3.14×36×4
=150.72(dm3)
它的体积是150.72dm3。
【点睛】本题考查圆锥体积公式的运用。
13.188.4
【分析】这个圆柱形笔筒的侧面展开图是一个长方形,则圆柱的侧面积等于长方形的面积,利用“长方形的面积=长×宽”求出这个笔筒的侧面积,据此解答。
【详解】18.84×10=188.4(平方厘米)
所以,这个圆柱形笔筒的侧面积是188.4平方厘米。
【点睛】本题主要考查圆柱的侧面积,理解长方形的面积等于圆柱的侧面积是解答题目的关键。
14. 2.88 1.92
【分析】用圆柱的体积乘每立方米材料的重量,即可求出这个圆柱形材料的重量;圆柱内最大的圆锥与原来圆柱是等底等高的,所以圆锥的体积是圆柱的体积的,则削去部分的体积是圆柱体积的(1-),据此求出减少部分的体积,再乘每立方米材料的重量,即可解答。
【详解】3.6×0.8=2.88(千克)
3.6×(1-)×0.8
=3.6××0.8
=2.4×0.8
=1.92(千克)
【点睛】抓住圆柱内最大圆锥的特点以及等底等高的圆柱的体积与圆锥的体积的倍数关系即可解决此类问题。
15. × 大圆锥的底面半径是小圆锥的2倍,则大圆锥的底面积是小圆锥底面积的4倍,高也是小圆锥的2倍,则大圆锥的体积是小圆锥体积的8倍。
【分析】根据圆锥的体积公式:V=,再根据因数与积的变化规律,积扩大倍数等于两个因数扩大倍数的乘积,据此判断即可。
【详解】根据圆的面积可知,若大圆锥的底面半径是小圆锥的2倍,则大圆锥的底面积是小圆锥底面积的4倍;同时大圆锥的高也是小圆锥高的2倍,根据圆锥的体积公式可知,则大圆锥的体积是小圆锥体积的8倍。即2×2×2=8。
所以要判定题干中的说法为:×
理由:大圆锥的底面半径是小圆锥的2倍,则大圆锥的底面积是小圆锥底面积的4倍,高也是小圆锥的2倍,则大圆锥的体积是小圆锥体积的8倍。
【点睛】此题主要考查圆锥的体积公式的灵活运用以及因数与积的变化规律,关键是熟记公式。
16. 圆柱 200.96
【分析】正方形的边长是4厘米,绕着这个正方形的一边旋转一周,得到的几何体是圆柱体。圆柱的高和半径相等,都是4厘米,利用圆柱的体积公式:,代入数据求出圆柱的体积。
【详解】上图是一个正方形,边长是4厘米,把这个正方形绕AB边旋转一周,形成的物体是圆柱体。
3.14×42×4
=3.14×16×4
=200.96(立方厘米)
【点睛】此题主要考查圆柱的特征以及灵活运用圆柱的体积公式。
17.25.12立方厘米
【分析】由图可知,圆锥的底面直径是4厘米,高是6厘米,利用“”求出圆锥的体积,据此解答。
【详解】×3.14×(4÷2)2×6
=×3.14×4×6
=×6×3.14×4
=(×6)×(3.14×4)
=2×12.56
=25.12(立方厘米)
所以,圆锥的体积是25.12立方厘米。
18.300毫升
【分析】根据圆柱的容积公式:容积=底面积×高;底面积=容积÷高,用瓶内饮料的容积除以此时的高度,即240÷20,求出这个饮料瓶底的底面积;空白处的容积等于底面积是圆柱形饮料瓶的底面积,高是5厘米的圆柱的容积,代入数据,求出空白处的容积,再加上瓶内饮料的容积,注意单位名数的换算;即可解答。
【详解】240毫升=240立方厘米
240÷20=12(平方厘米)
12×5=60(立方厘米)
60立方厘米=60毫升
60+240=300(毫升)
答:瓶子的容积是300毫升。
19.4厘米
【分析】由题意可知:圆锥的体积等于长方体铁块与正方体铁块的体积和。先根据“长方体的体积=长×宽×高”求出长方体铁块的体积;再根据“正方体的体积=棱长×棱长×棱长”求出正方体铁块的体积;再用长方体铁块的体积加上正方体铁块的体积求出圆锥的体积;最后根据“圆锥的高=圆锥的体积÷÷底面积”求出圆锥的高。
【详解】1.2平方分米=120平方厘米
8×4×3+4×4×4
=96+64
=160(立方厘米)
160÷÷120
=160×3÷120
=480÷120
=4(厘米)
答:高是4厘米。
【点睛】此题考查了长方体、正方体、圆锥的体积计算公式。解决此题关键是明确熔铸前后铁块的形状发生了变化,但体积不变。
20.18.84立方厘米
【分析】瓶子的容积=水的体积+空白部分的容积,倒置放平后,空白部分是个高(7-5)厘米的圆柱,根据圆柱体积=底面积×高,分别求出水的体积和空白部分的容积,相加即可。
【详解】3.14×(2÷2)2×4+3.14×(2÷2)2×(7-5)
=3.14×12×4+3.14×12×2
=3.14×1×4+3.14×1×2
=12.56+6.28
=18.84(立方厘米)
答:瓶子的容积是18.84立方厘米。
【点睛】关键是利用转化思想,将不规则部分的容积转化为圆柱进行计算。
21.150.72平方厘米
【分析】根据题意,把圆柱切拼成近似长方体,那么这个长方体的长等于圆柱底面周长的一半,长方体的宽等于圆柱的底面半径,长方体的高等于圆柱的高;
已知长方体右侧面积为15平方厘米,即已知长方体右面“宽×高”的积,用右侧面积除以高,即可求出长方体的宽,也是圆柱的底面半径;
再根据圆柱的表面积S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算即可。
【详解】圆柱的底面半径:
15÷5=3(厘米)
圆柱的表面积:
2×3.14×3×5+3.14×32×2
=3.14×30+3.14×9×2
=94.2+56.52
=150.72(平方厘米)
答:原来圆柱的表面积是150.72平方厘米。
【点睛】本题考查圆柱表面积公式的运用,掌握圆柱体积公式的推导过程,理解拼成的近似长方体和圆柱之间的联系,求出圆柱的底面半径是解题的关键。
22.62.8立方米
【分析】观察图形可知,图形的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算,即可求出这个粮仓最多能存储粮食的体积。
【详解】圆柱的体积:
3.14×(4÷2)2×4
=3.14×4×4
=50.24(立方米)
圆锥的体积:
×3.14×(4÷2)2×(7-4)
=×3.14×4×3
=12.56(立方米)
一共:50.24+12.56=62.8(立方米)
答:这个漏斗形粮仓最多能存储粮食62.8立方米。
【点睛】本题考查圆柱、圆锥体积公式的运用,结合图形,分析出组合体的体积是由哪些立体图形的体积相加或相减得到,再利用图形的体积公式列式计算。
23.37.68平方米
【分析】由题意可知,计算抹水泥部分的面积就是求圆柱的侧面积与一个底面积的和,利用“”求出需要抹水泥部分的面积,据此解答。
【详解】3.14×4×2+3.14×(4÷2)2
=3.14×4×2+3.14×4
=12.56×2+12.56
=25.12+12.56
=37.68(平方米)
答:抹水泥部分的面积是37.68平方米。
【点睛】本题主要考查圆柱表面积公式的应用,明确需要计算圆柱哪些面的面积是解答题目的关键。
24.(1)28.26平方厘米;
(2)423.9立方厘米
【分析】(1)求茶杯占据桌面的大小就是求圆柱的底面积,利用“”求出茶杯的底面积;
(2)求茶杯装满水后的体积就是求圆柱的体积,利用“”求出茶杯的体积,据此解答。
【详解】(1)3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
答:这只茶杯占据桌面的大小是28.26平方厘米。
(2)28.26×15=423.9(立方厘米)
答:这只茶杯装满水后的体积是423.9立方厘米。
【点睛】掌握圆的面积和圆柱的体积计算公式是解答题目的关键。
25.1.2分米
【分析】圆锥装饰物放入鱼缸后,先换算单位,水面上升的高度为0.2分米,圆锥装饰物的体积等于水面上升的体积,水面上升的体积可看作长宽均为5分米,高为0.2分米的长方体的体积,根据长方体的体积公式:V=abh,代入数据即可求出这个圆锥装饰物的体积,再利用圆锥的体积公式:V=Sh,用圆锥装饰物的体积除以圆锥的底面积,即可求出这个圆锥装饰物的高。
【详解】2厘米=0.2分米
5×5×0.2÷÷12.5
=5÷÷12.5
=15÷12.5
=1.2(分米)
答:这个圆锥装饰物的高是1.2分米。
【点睛】此题的解题关键是掌握求不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积和圆锥的体积公式求解。
26.113.04立方厘米
【分析】由题干可知,圆柱和圆锥是等底的,求圆柱和圆锥的体积之和就是陀螺的体积。分别利用圆柱和圆锥的体积公式求解即可。
【详解】3.14×(6÷2)2×3+×3.14×(6÷2)2×3
=3.14×32×3+×3×3.14×32
=3.14×9×3+3.14×9
=84.78+28.26
=113.04(立方厘米)
答:这个陀螺的体积是113.04立方厘米。
【点睛】此题考查的是圆柱和圆锥的体积公式的应用,熟记公式是解题关键。
27.0.2826米
【分析】由题意可知,沙堆的体积是一定的,根据圆锥的体积=×底面积×高,求出圆锥形沙堆的体积,再根据长方体的体积=长×宽×高,求出高即沙的厚度。
【详解】×3.14×0.92×1.5÷(3×1.5)
=×3.14×0.81×1.5÷4.5
=×2.5434×1.5÷4.5
=×3.8151÷4.5
=1.2717÷4.5
=0.2826(米)
答:能铺0.2826米厚。
【点睛】本题考查圆锥和长方体的体积,熟记圆锥和长方体的体积公式是解题的关键。
28.(1)6
(2)56.52立方厘米
【分析】(1)根据等底等高的圆柱的体积是圆锥体积的3倍,两个杯子是完全一样的,A杯的水面上升了2厘米,则B杯的水面上升了(2×3)厘米;(2)圆锥的体积即上升的2厘米水的体积,根据圆柱的体积,据此解答。
【详解】(1)2×3=6(厘米)
(2)
(立方厘米)
答:圆锥零件的体积是56.52立方厘米。
【点睛】灵活掌握圆柱的体积计算公式是解答本题的关键,涉及到的知识点是等底等高的圆柱的体积是圆锥体积的3倍。
29.(1)1130.4mL;
(2)不够
【分析】(1)根据圆柱的容积(体积)公式:,把数据代入公式解答。
(2)根据长方体的体积(容积)公式:,把数据代入公式求出每个玻璃杯的容积,再求出5杯的容积,然后与圆柱形容器的容积进行比较即可。
【详解】(1)3.14×(12÷2)2×10
=3.14×36×10
=113.04×10
=1130.4(cm2)
1130.4cm2=1130.4mL
答:榨出的果汁有1130.4mL。
(2)25×10×5
=250×5
=1250(mL)
1130.4mL<1250mL
答:不够小维家5口人每人一满杯。
【点睛】此题主要考查圆柱的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
30.立方厘米;毫升
【分析】根据题意可知,圆柱形量杯中,都盛有500毫升的水,加入圆锥形零件后,乙量杯水的容积是600毫升水,把容积换成体积;用加入圆锥形零件后水的体积减去加入圆锥形零件前水的体积,即可求出圆锥形零件的体积;再根据等底等高的圆锥体体积是圆柱体积的,求出圆柱形零件的体积,再加上原来甲量杯中水的体积,就是加入圆柱形零件后水与圆柱形零件的体积,再化成容积,即可求出量杯中水面的刻度。
【详解】500毫升=500立方厘米
600毫升=600立方厘米
圆锥的体积:600-500=100(立方厘米)
圆柱的体积:100×3=300(立方厘米)
300+500=800(立方厘米)
800立方厘米=800毫升
答:圆锥零件的体积是100立方厘米,甲量杯水面刻度是800毫升。
【点睛】解答本题的关键是明确等底等高的圆锥体积是圆柱的;以及单位名数的互换。
