多边形的内角和课堂通行证 苏教版数学四年级下册(含答案)
文档属性
| 名称 | 多边形的内角和课堂通行证 苏教版数学四年级下册(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 498.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
多边形的内角和
一、选择题
1.下面说法不正确的是( )。
A.五边形可以分为3个三角形,所以内角和可以用来计算
B.两个三角形可以拼成一个平行四边形
C.如果一个三角形的三个角都相等,那么这个三角形一定是锐角三角形
D.过平行四边形的一个顶点最多能画2条高
2.下列说法中正确的有( )句。
①梯形一定不是轴对称图形。
②一个长方形拉成平行四边形之后内角和不变。
③有两个锐角的三角形一定是锐角三角形。
④两个同样的长方形,长15米,宽9米,第一个长方形的长减少2米,宽不变;第二个长方形的宽减少2米,长不变。变化后第一个长方形的面积大一些。21cnjy.com
A.1 B.2 C.3 D.4
3.如图在一个三角形中剪去了一个35°的内角,剩下图形的内角和是( )°。
A.180 B.360 C.145 D.155
4.一个等腰三角形,顶角的度数是底角的2倍,底角是( )。
A.20° B.45° C.60° D.90°
5.下面三个图形在一组平行线之间,比较( )。
A.3个图形的高一样长 B.3个图形的底一样长
C.3个图形的周长一样长 D.3个图形的内角和一样大
6.五边形的内角和的计算方法是( )。
A.5×180°-2 B.(5-2)×180°
C.(5-1)×180° D.(5-3)×180°
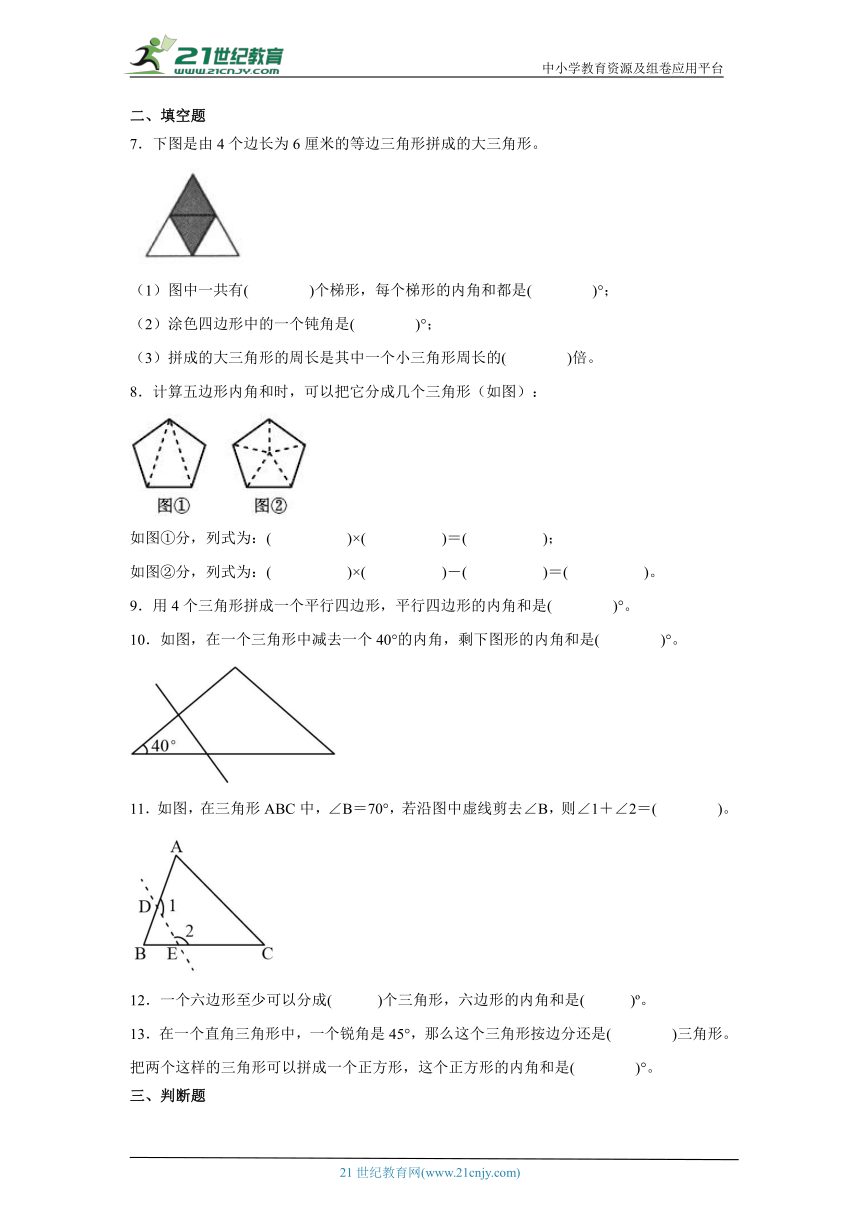
二、填空题
7.下图是由4个边长为6厘米的等边三角形拼成的大三角形。
(1)图中一共有( )个梯形,每个梯形的内角和都是( )°;
(2)涂色四边形中的一个钝角是( )°;
(3)拼成的大三角形的周长是其中一个小三角形周长的( )倍。
8.计算五边形内角和时,可以把它分成几个三角形(如图):
如图①分,列式为:( )×( )=( );
如图②分,列式为:( )×( )-( )=( )。
9.用4个三角形拼成一个平行四边形,平行四边形的内角和是( )°。
10.如图,在一个三角形中减去一个40°的内角,剩下图形的内角和是( )°。
11.如图,在三角形ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2=( )。
12.一个六边形至少可以分成( )个三角形,六边形的内角和是( ) 。
13.在一个直角三角形中,一个锐角是45°,那么这个三角形按边分还是( )三角形。把两个这样的三角形可以拼成一个正方形,这个正方形的内角和是( )°。
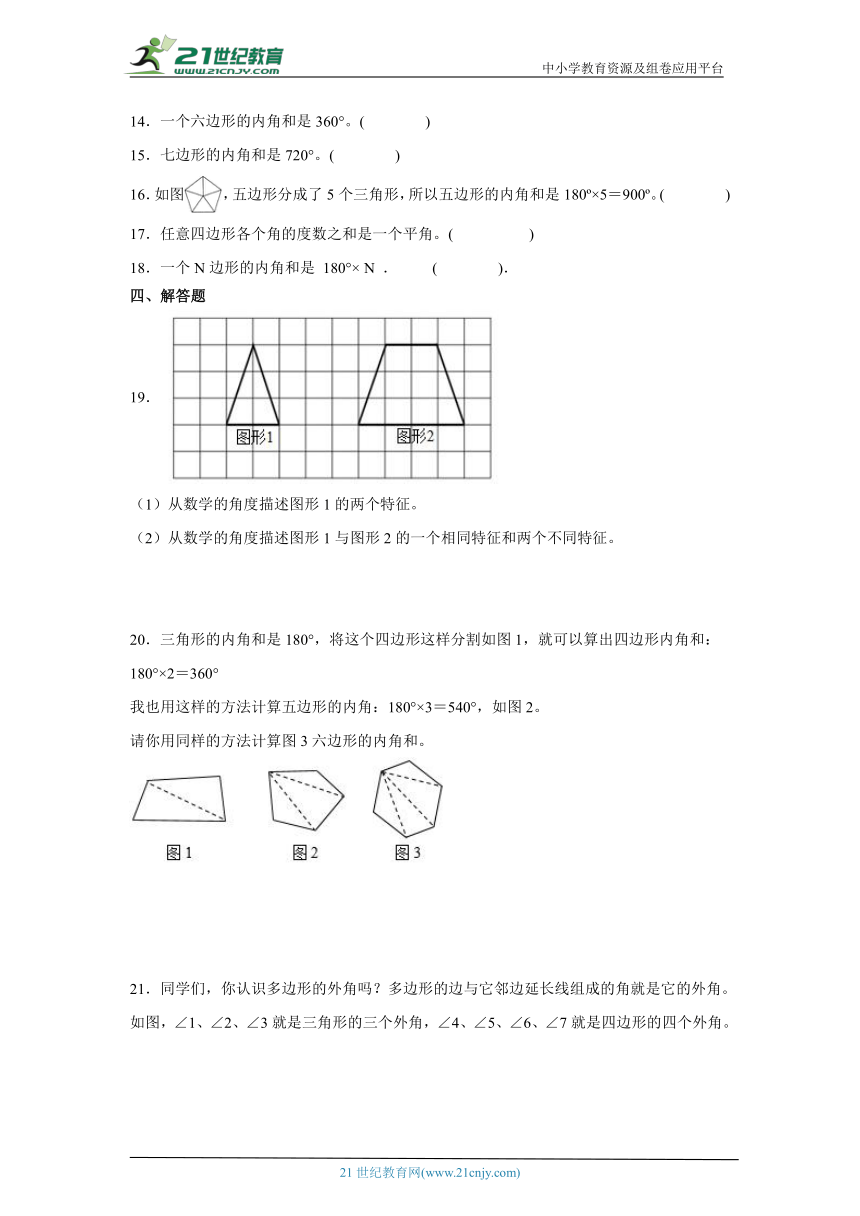
三、判断题
14.一个六边形的内角和是360°。( )
15.七边形的内角和是720°。( )
16.如图,五边形分成了5个三角形,所以五边形的内角和是180 ×5=900 。( )
17.任意四边形各个角的度数之和是一个平角。( )
18.一个N边形的内角和是 180°× N . ( ).
四、解答题
19.
(1)从数学的角度描述图形1的两个特征。
(2)从数学的角度描述图形1与图形2的一个相同特征和两个不同特征。
20.三角形的内角和是180°,将这个四边形这样分割如图1,就可以算出四边形内角和:180°×2=360°21世纪教育网版权所有
我也用这样的方法计算五边形的内角:180°×3=540°,如图2。
请你用同样的方法计算图3六边形的内角和。
21.同学们,你认识多边形的外角吗?多边形的边与它邻边延长线组成的角就是它的外角。如图,∠1、∠2、∠3就是三角形的三个外角,∠4、∠5、∠6、∠7就是四边形的四个外角。
(1)仔细观察每个图形的内角与外角之间关系,画一画、算一算想办法推算出每个图形的外角的和各是多少度?21·cn·jy·com
推算过程。
(2)初步得出结论:三角形三个外角和是( )°;四边形四个外角的和是( )°。
(3)根据上面的发现,你有什么猜想?
22.三角形的内角和是180 ,那么,
(1)任意四边形的内角和是________°,任意五边形的内角和是________°;
(2)进一步,如果把多边形的边数记作n,那么,n 边形的内角和的计算公式是___________________。www.21-cn-jy.com
(3)一个考古学家发现了一个正多边形的残片,已知,∠EAB=∠ABF=165 ,那么这个正多边形一共有多少条边?21教育网
参考答案:
1.B
2.B
3.B
4.B
5.A
6.B
7. 3 360 120 2
8. 180° 3 540° 180° 5 360° 540°2·1·c·n·j·y
9.360
10.360
11.250°
12. 4 720
13. 等腰 360
14.×
15.×
16.×
17.×
18.×
19.(1)三个锐角,两条边相等
(2)相同特征:有两条边相等。两个不同特征:图形1的内角和是180°,有3条边。图形2的内角和是360°,有4条边【来源:21·世纪·教育·网】
20.720°
21.略
22.(1)360;540;(2)180(n-2);(3)24边
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
多边形的内角和
一、选择题
1.下面说法不正确的是( )。
A.五边形可以分为3个三角形,所以内角和可以用来计算
B.两个三角形可以拼成一个平行四边形
C.如果一个三角形的三个角都相等,那么这个三角形一定是锐角三角形
D.过平行四边形的一个顶点最多能画2条高
2.下列说法中正确的有( )句。
①梯形一定不是轴对称图形。
②一个长方形拉成平行四边形之后内角和不变。
③有两个锐角的三角形一定是锐角三角形。
④两个同样的长方形,长15米,宽9米,第一个长方形的长减少2米,宽不变;第二个长方形的宽减少2米,长不变。变化后第一个长方形的面积大一些。21cnjy.com
A.1 B.2 C.3 D.4
3.如图在一个三角形中剪去了一个35°的内角,剩下图形的内角和是( )°。
A.180 B.360 C.145 D.155
4.一个等腰三角形,顶角的度数是底角的2倍,底角是( )。
A.20° B.45° C.60° D.90°
5.下面三个图形在一组平行线之间,比较( )。
A.3个图形的高一样长 B.3个图形的底一样长
C.3个图形的周长一样长 D.3个图形的内角和一样大
6.五边形的内角和的计算方法是( )。
A.5×180°-2 B.(5-2)×180°
C.(5-1)×180° D.(5-3)×180°
二、填空题
7.下图是由4个边长为6厘米的等边三角形拼成的大三角形。
(1)图中一共有( )个梯形,每个梯形的内角和都是( )°;
(2)涂色四边形中的一个钝角是( )°;
(3)拼成的大三角形的周长是其中一个小三角形周长的( )倍。
8.计算五边形内角和时,可以把它分成几个三角形(如图):
如图①分,列式为:( )×( )=( );
如图②分,列式为:( )×( )-( )=( )。
9.用4个三角形拼成一个平行四边形,平行四边形的内角和是( )°。
10.如图,在一个三角形中减去一个40°的内角,剩下图形的内角和是( )°。
11.如图,在三角形ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2=( )。
12.一个六边形至少可以分成( )个三角形,六边形的内角和是( ) 。
13.在一个直角三角形中,一个锐角是45°,那么这个三角形按边分还是( )三角形。把两个这样的三角形可以拼成一个正方形,这个正方形的内角和是( )°。
三、判断题
14.一个六边形的内角和是360°。( )
15.七边形的内角和是720°。( )
16.如图,五边形分成了5个三角形,所以五边形的内角和是180 ×5=900 。( )
17.任意四边形各个角的度数之和是一个平角。( )
18.一个N边形的内角和是 180°× N . ( ).
四、解答题
19.
(1)从数学的角度描述图形1的两个特征。
(2)从数学的角度描述图形1与图形2的一个相同特征和两个不同特征。
20.三角形的内角和是180°,将这个四边形这样分割如图1,就可以算出四边形内角和:180°×2=360°21世纪教育网版权所有
我也用这样的方法计算五边形的内角:180°×3=540°,如图2。
请你用同样的方法计算图3六边形的内角和。
21.同学们,你认识多边形的外角吗?多边形的边与它邻边延长线组成的角就是它的外角。如图,∠1、∠2、∠3就是三角形的三个外角,∠4、∠5、∠6、∠7就是四边形的四个外角。
(1)仔细观察每个图形的内角与外角之间关系,画一画、算一算想办法推算出每个图形的外角的和各是多少度?21·cn·jy·com
推算过程。
(2)初步得出结论:三角形三个外角和是( )°;四边形四个外角的和是( )°。
(3)根据上面的发现,你有什么猜想?
22.三角形的内角和是180 ,那么,
(1)任意四边形的内角和是________°,任意五边形的内角和是________°;
(2)进一步,如果把多边形的边数记作n,那么,n 边形的内角和的计算公式是___________________。www.21-cn-jy.com
(3)一个考古学家发现了一个正多边形的残片,已知,∠EAB=∠ABF=165 ,那么这个正多边形一共有多少条边?21教育网
参考答案:
1.B
2.B
3.B
4.B
5.A
6.B
7. 3 360 120 2
8. 180° 3 540° 180° 5 360° 540°2·1·c·n·j·y
9.360
10.360
11.250°
12. 4 720
13. 等腰 360
14.×
15.×
16.×
17.×
18.×
19.(1)三个锐角,两条边相等
(2)相同特征:有两条边相等。两个不同特征:图形1的内角和是180°,有3条边。图形2的内角和是360°,有4条边【来源:21·世纪·教育·网】
20.720°
21.略
22.(1)360;540;(2)180(n-2);(3)24边
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
