11.2 图形在坐标系中的平移 课时作业 (含答案)2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 11.2 图形在坐标系中的平移 课时作业 (含答案)2023-2024学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 273.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 15:28:01 | ||
图片预览


文档简介
11.2 图形在坐标系中的平移
【练基础】
必备知识1 点在平面直角坐标系中的平移
1.【肥西期末】在平面直角坐标系中,点A(-1,2)向上平移3个单位长度后的坐标是 ( )
A.(2,2) B.(-4,2)
C.(-1,5) D.(-1,-1)
2.在平面直角坐标系中,将点A(1,2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B所在象限为 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.【蚌埠期末】如果将点A(-3,-2)向右平移2个单位长度后,再向下平移3个单位长度得到点B,那么点B的坐标是 .
4.将点P先向下平移3个单位长度,再向左平移2个单位长度后得到点Q(3,-1),则点P的坐标为 .
必备知识2 图形在平面直角坐标系中的平移
5.在平面直角坐标系中,已知点A(-1,2),B(1,0),平移线段AB,使点A落在点A1(2,3)处,则点B的对应点B1的坐标为 ( )
A.(-2,-1) B.(4,1)
C.(4,0) D.(-2,1)
6.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,若DB=1,则点C的坐标为 ( )
A.(2,2) B.(4,3) C.(3,2) D.(4,2)
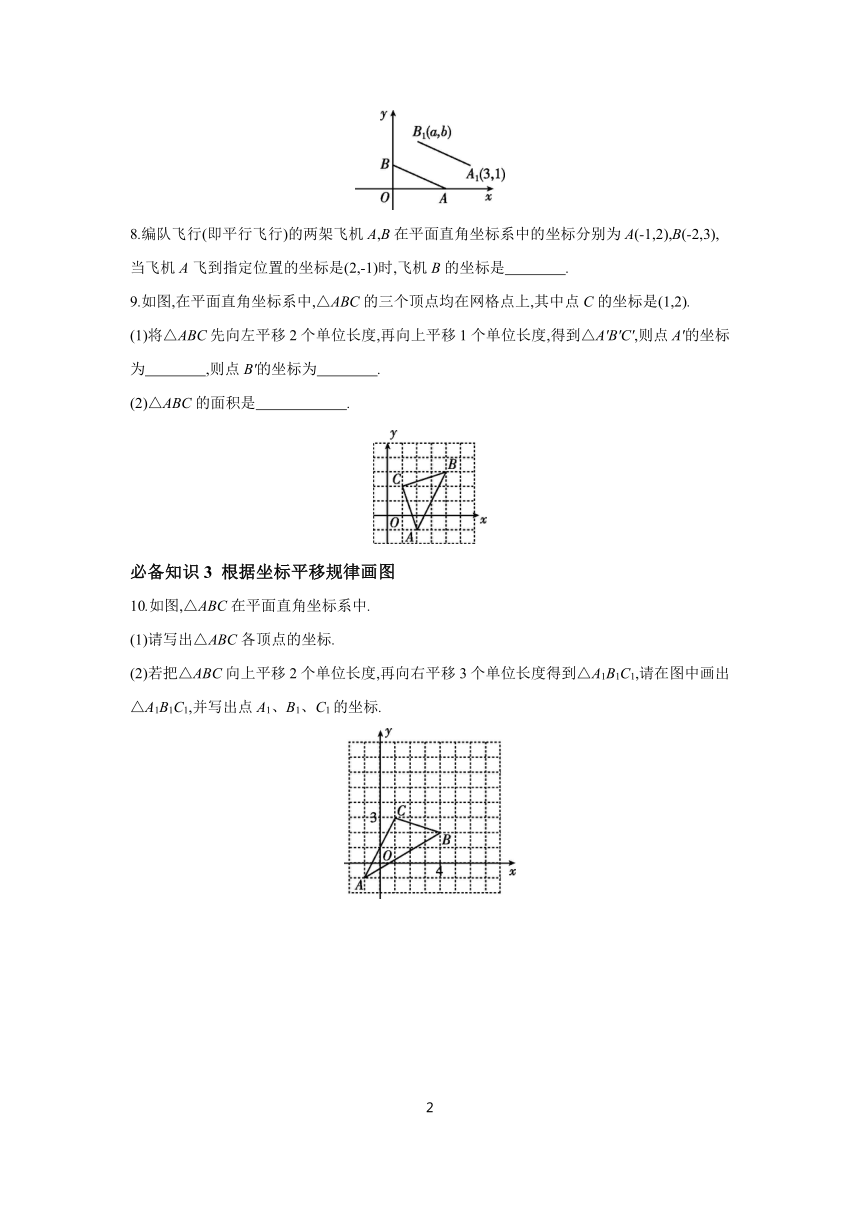
7.如图,点A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,A1、B1的坐标分别为(3,1)、(a,b),则a-b的值为 .
8.编队飞行(即平行飞行)的两架飞机A,B在平面直角坐标系中的坐标分别为A(-1,2),B(-2,3),当飞机A飞到指定位置的坐标是(2,-1)时,飞机B的坐标是 .
9.如图,在平面直角坐标系中,△ABC的三个顶点均在网格点上,其中点C的坐标是(1,2).
(1)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',则点A'的坐标为 ,则点B'的坐标为 .
(2)△ABC的面积是 .
必备知识3 根据坐标平移规律画图
10.如图,△ABC在平面直角坐标系中.
(1)请写出△ABC各顶点的坐标.
(2)若把△ABC向上平移2个单位长度,再向右平移3个单位长度得到△A1B1C1,请在图中画出△A1B1C1,并写出点A1、B1、C1的坐标.
【练能力】
11.在平面直角坐标系中,线段CF是由线段AB平移得到的,点A(-2,3)的对应点为C(1,2),则点B(a,b)的对应点F的坐标为( )
A.(a+3,b+1) B.(a+3,b-1)
C.(a-3,b+1) D.(a-3,b-1)
12.在平面直角坐标系中,点A(m,n)经过平移后得到的对应点A'(m+3,n-4)在第二象限,则点A所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
13.已知点A(1,5),B(4,2),将线段AB平移至CD(点A与点C为对应点),使得点C在x轴上,点D到y轴的距离为2,则点D的坐标为 .
14.如图,△A'B'C'是由△ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,观察点与点的坐标之间的关系,解答下列问题.
(1)直接写出点A和点A'的坐标,并说明△A'B'C'是由△ABC经过怎样的平移得到的.
(2)若点M(a+2,4-b)是点N(2a-3,2b-5)通过(1)中的平移变换得到的,求(b-a)2的值.
【练素养】
15.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点A-,0,B为y轴上的一个动点.
(1)若已知点B(0,2),则点A与点B的“非常距离”为 .
(2)若点A与点B的“非常距离”为3,则点B的坐标为 .
(3)点A与点B的“非常距离”的最小值为 .
参考答案
基础演练
1.C 2.B 3.(-1,-5) 4.(5,2) 5.B 6.D
7.-1 8.(1,0)
9.【解析】(1)(0,0);(2,4).
提示:∵点A的坐标为(2,-1),点B的坐标为(4,3),
∴向左平移2个单位长度,再向上平移1个单位长度后点A'的坐标为(0,0),点B'的坐标为(2,4).
(2)5.
提示:△ABC的面积为×(3+1)×4-×1×3-×1×3=5.
10.【解析】(1)A(-1,-1),B(4,2),C(1,3).
(2)如图,把△ABC向上平移2个单位长度,再向右平移3个单位长度得到△A1B1C1,可得A1(2,1)、B1(7,4)、C1(4,5),连接点A1,B1,C1,△A1B1C1即为所求.
能力生成
11.B 12.B
13.(2,-3)或(-2,-3)
14.【解析】(1)由题意得A(0,3),A'(-3,0),
△A'B'C'是由△ABC向左平移3个单位长度,再向下平移3个单位长度得到的.
(2)由题意得
解得
∴(b-a)2=16.
素养通关
15.(1)2
(2)(0,3)或(0,-3)
(3)
2
【练基础】
必备知识1 点在平面直角坐标系中的平移
1.【肥西期末】在平面直角坐标系中,点A(-1,2)向上平移3个单位长度后的坐标是 ( )
A.(2,2) B.(-4,2)
C.(-1,5) D.(-1,-1)
2.在平面直角坐标系中,将点A(1,2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B所在象限为 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.【蚌埠期末】如果将点A(-3,-2)向右平移2个单位长度后,再向下平移3个单位长度得到点B,那么点B的坐标是 .
4.将点P先向下平移3个单位长度,再向左平移2个单位长度后得到点Q(3,-1),则点P的坐标为 .
必备知识2 图形在平面直角坐标系中的平移
5.在平面直角坐标系中,已知点A(-1,2),B(1,0),平移线段AB,使点A落在点A1(2,3)处,则点B的对应点B1的坐标为 ( )
A.(-2,-1) B.(4,1)
C.(4,0) D.(-2,1)
6.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,若DB=1,则点C的坐标为 ( )
A.(2,2) B.(4,3) C.(3,2) D.(4,2)
7.如图,点A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,A1、B1的坐标分别为(3,1)、(a,b),则a-b的值为 .
8.编队飞行(即平行飞行)的两架飞机A,B在平面直角坐标系中的坐标分别为A(-1,2),B(-2,3),当飞机A飞到指定位置的坐标是(2,-1)时,飞机B的坐标是 .
9.如图,在平面直角坐标系中,△ABC的三个顶点均在网格点上,其中点C的坐标是(1,2).
(1)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',则点A'的坐标为 ,则点B'的坐标为 .
(2)△ABC的面积是 .
必备知识3 根据坐标平移规律画图
10.如图,△ABC在平面直角坐标系中.
(1)请写出△ABC各顶点的坐标.
(2)若把△ABC向上平移2个单位长度,再向右平移3个单位长度得到△A1B1C1,请在图中画出△A1B1C1,并写出点A1、B1、C1的坐标.
【练能力】
11.在平面直角坐标系中,线段CF是由线段AB平移得到的,点A(-2,3)的对应点为C(1,2),则点B(a,b)的对应点F的坐标为( )
A.(a+3,b+1) B.(a+3,b-1)
C.(a-3,b+1) D.(a-3,b-1)
12.在平面直角坐标系中,点A(m,n)经过平移后得到的对应点A'(m+3,n-4)在第二象限,则点A所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
13.已知点A(1,5),B(4,2),将线段AB平移至CD(点A与点C为对应点),使得点C在x轴上,点D到y轴的距离为2,则点D的坐标为 .
14.如图,△A'B'C'是由△ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,观察点与点的坐标之间的关系,解答下列问题.
(1)直接写出点A和点A'的坐标,并说明△A'B'C'是由△ABC经过怎样的平移得到的.
(2)若点M(a+2,4-b)是点N(2a-3,2b-5)通过(1)中的平移变换得到的,求(b-a)2的值.
【练素养】
15.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点A-,0,B为y轴上的一个动点.
(1)若已知点B(0,2),则点A与点B的“非常距离”为 .
(2)若点A与点B的“非常距离”为3,则点B的坐标为 .
(3)点A与点B的“非常距离”的最小值为 .
参考答案
基础演练
1.C 2.B 3.(-1,-5) 4.(5,2) 5.B 6.D
7.-1 8.(1,0)
9.【解析】(1)(0,0);(2,4).
提示:∵点A的坐标为(2,-1),点B的坐标为(4,3),
∴向左平移2个单位长度,再向上平移1个单位长度后点A'的坐标为(0,0),点B'的坐标为(2,4).
(2)5.
提示:△ABC的面积为×(3+1)×4-×1×3-×1×3=5.
10.【解析】(1)A(-1,-1),B(4,2),C(1,3).
(2)如图,把△ABC向上平移2个单位长度,再向右平移3个单位长度得到△A1B1C1,可得A1(2,1)、B1(7,4)、C1(4,5),连接点A1,B1,C1,△A1B1C1即为所求.
能力生成
11.B 12.B
13.(2,-3)或(-2,-3)
14.【解析】(1)由题意得A(0,3),A'(-3,0),
△A'B'C'是由△ABC向左平移3个单位长度,再向下平移3个单位长度得到的.
(2)由题意得
解得
∴(b-a)2=16.
素养通关
15.(1)2
(2)(0,3)或(0,-3)
(3)
2
