13.1 课时1 三角形中边的关系 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 13.1 课时1 三角形中边的关系 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览


文档简介
13.1 课时1 三角形中边的关系
【练基础】
必备知识1 三角形的有关概念
1.如图,以BC为边的三角形共有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画 个三角形.
必备知识2 三角形按边分类
3.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是 ( )
A B
C D
必备知识3 三角形的三边关系
4.下列四组线段中,不可以构成三角形的是 ( )
A.4,5,6 B.1.5,2,2.5
C.,, D.1,7,3
5.【马鞍山期末】小芳有长度分别为4 cm和8 cm的两根木条,桌上有下列长度的四根木条,她要用其中的一根与原有的两根木条钉成一个首尾相接的三角形木框,则这根木条的长度为 ( )
A.3 cm B.5 cm C.12 cm D.17 cm
6.三角形三边比是3∶4∶5,周长是72,那么,最长边是 ( )
A.30 B.24 C.18 D.12
7.【肥东期末】△ABC的三边长分别为1,3,x,且x为整数,则x的值是 .
必备知识4 求等腰三角形的边长与周长
8.【蚌埠期末】已知等腰三角形有一边长为5,一边长为2,则其周长为 ( )
A.12 B.9 C.10 D.12或9
9.【淮南期末】等腰三角形的周长为14 cm,其中一边长为4 cm,则该等腰三角形的腰长为 ( )
A.4 cm B.5 cm
C.4 cm或5 cm D.4 cm或6 cm
10.【包河期中】已知一个等腰三角形的周长是12 cm,其中一边长是2 cm,求另外两边的长.
【练能力】
11.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 对.
12.【安庆期中】一个等腰三角形的周长为40 cm.
(1)设腰长为x,用含有x的代数式表示三角形的底边,并求出腰长的取值范围.
(2)若一边长为10 cm,求另外两边长.
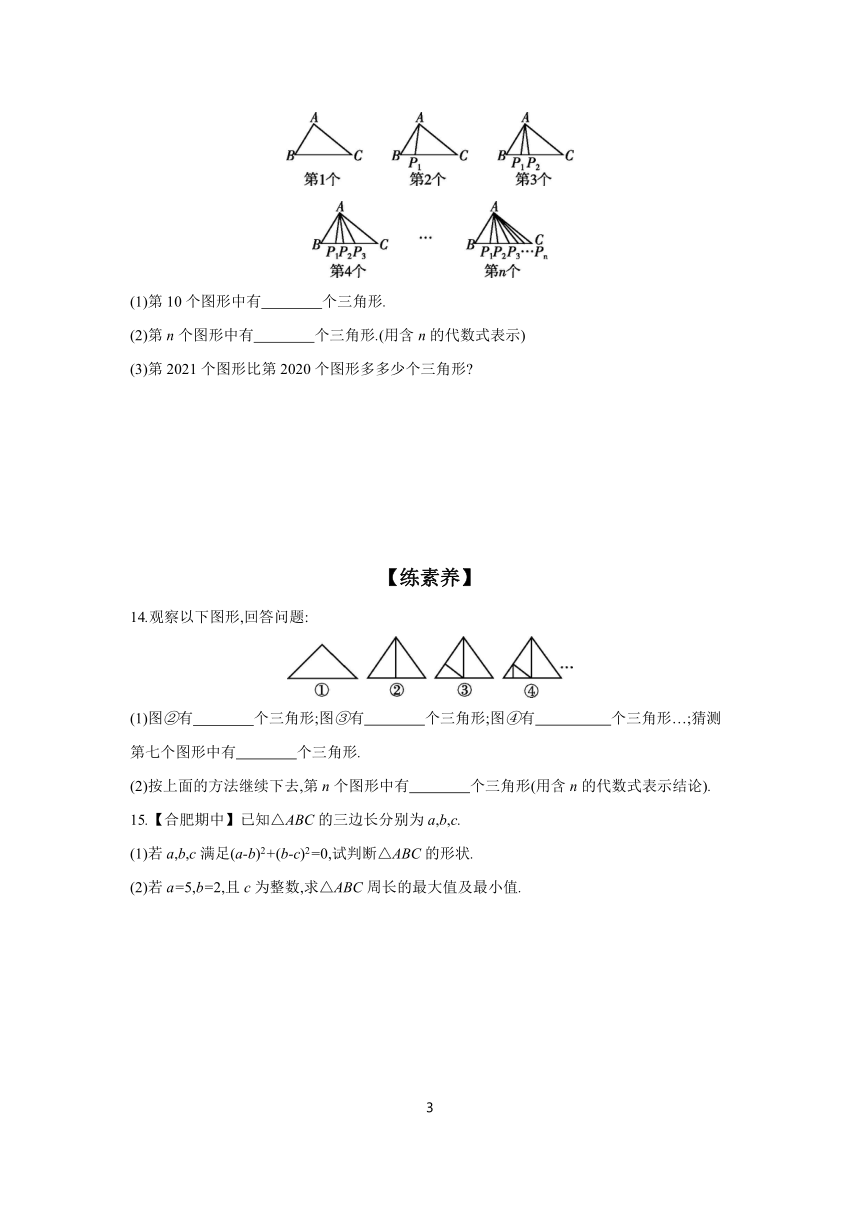
13.观察下图中的规律,并解答下列问题.
(1)第10个图形中有 个三角形.
(2)第n个图形中有 个三角形.(用含n的代数式表示)
(3)第2021个图形比第2020个图形多多少个三角形
【练素养】
14.观察以下图形,回答问题:
(1)图②有 个三角形;图③有 个三角形;图④有 个三角形…;猜测第七个图形中有 个三角形.
(2)按上面的方法继续下去,第n个图形中有 个三角形(用含n的代数式表示结论).
15.【合肥期中】已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状.
(2)若a=5,b=2,且c为整数,求△ABC周长的最大值及最小值.
参考答案
基础演练
1.C 2.10 3.C 4.D 5.B 6.A 7.3 8.A 9.C
10.【解析】①若底边长为2 cm,则腰长为×(12-2)=5 cm,即另外两边的长分别为5 cm,5 cm,能构成三角形;
②若腰长为2 cm,则另外两边的长分别为2 cm,8 cm.
∵2+2=4<8,故不能构成三角形.
综上所述,另外两边的长为5 cm,5 cm.
能力生成
11.3
12.【解析】(1)设腰长为x,则底边为40-2x.
由题意得解得10(2)有两种情况,
①当等腰三角形的一腰长为10 cm时,其底边长为40-10-10=20 cm,不能构成三角形.
②当等腰三角形底边长为10 cm时,其腰长为=15 cm.
故另外两边长分别为15 cm,15 cm.
13.【解析】(1)55.
(2).
(3)-=2021.
∴第2021个图形比第2020个图形多2021个三角形.
素养通关
14.【解析】(1)3;5;7;13.
提示:图②有3个三角形;图③有5个三角形;图④有7个三角形;…;猜测第七个图形中有13个三角形.
(2)(2n-1).
提示:∵图②有3个三角形,3=2×2-1;
图③有5个三角形,5=2×3-1;
图④有7个三角形,7=2×4-1;
∴第n个图形中有(2n-1)个三角形.
15.【解析】(1)∵(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,∴a=b=c,
∴△ABC是等边三角形.
(2)∵a=5,b=2,且c为整数,
∴5-2∴c=4或5或6.
当c=4时,△ABC周长的最小值=5+2+4=11;
当c=6时,△ABC周长的最大值=5+2+6=13.
2
【练基础】
必备知识1 三角形的有关概念
1.如图,以BC为边的三角形共有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画 个三角形.
必备知识2 三角形按边分类
3.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是 ( )
A B
C D
必备知识3 三角形的三边关系
4.下列四组线段中,不可以构成三角形的是 ( )
A.4,5,6 B.1.5,2,2.5
C.,, D.1,7,3
5.【马鞍山期末】小芳有长度分别为4 cm和8 cm的两根木条,桌上有下列长度的四根木条,她要用其中的一根与原有的两根木条钉成一个首尾相接的三角形木框,则这根木条的长度为 ( )
A.3 cm B.5 cm C.12 cm D.17 cm
6.三角形三边比是3∶4∶5,周长是72,那么,最长边是 ( )
A.30 B.24 C.18 D.12
7.【肥东期末】△ABC的三边长分别为1,3,x,且x为整数,则x的值是 .
必备知识4 求等腰三角形的边长与周长
8.【蚌埠期末】已知等腰三角形有一边长为5,一边长为2,则其周长为 ( )
A.12 B.9 C.10 D.12或9
9.【淮南期末】等腰三角形的周长为14 cm,其中一边长为4 cm,则该等腰三角形的腰长为 ( )
A.4 cm B.5 cm
C.4 cm或5 cm D.4 cm或6 cm
10.【包河期中】已知一个等腰三角形的周长是12 cm,其中一边长是2 cm,求另外两边的长.
【练能力】
11.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 对.
12.【安庆期中】一个等腰三角形的周长为40 cm.
(1)设腰长为x,用含有x的代数式表示三角形的底边,并求出腰长的取值范围.
(2)若一边长为10 cm,求另外两边长.
13.观察下图中的规律,并解答下列问题.
(1)第10个图形中有 个三角形.
(2)第n个图形中有 个三角形.(用含n的代数式表示)
(3)第2021个图形比第2020个图形多多少个三角形
【练素养】
14.观察以下图形,回答问题:
(1)图②有 个三角形;图③有 个三角形;图④有 个三角形…;猜测第七个图形中有 个三角形.
(2)按上面的方法继续下去,第n个图形中有 个三角形(用含n的代数式表示结论).
15.【合肥期中】已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状.
(2)若a=5,b=2,且c为整数,求△ABC周长的最大值及最小值.
参考答案
基础演练
1.C 2.10 3.C 4.D 5.B 6.A 7.3 8.A 9.C
10.【解析】①若底边长为2 cm,则腰长为×(12-2)=5 cm,即另外两边的长分别为5 cm,5 cm,能构成三角形;
②若腰长为2 cm,则另外两边的长分别为2 cm,8 cm.
∵2+2=4<8,故不能构成三角形.
综上所述,另外两边的长为5 cm,5 cm.
能力生成
11.3
12.【解析】(1)设腰长为x,则底边为40-2x.
由题意得解得10
①当等腰三角形的一腰长为10 cm时,其底边长为40-10-10=20 cm,不能构成三角形.
②当等腰三角形底边长为10 cm时,其腰长为=15 cm.
故另外两边长分别为15 cm,15 cm.
13.【解析】(1)55.
(2).
(3)-=2021.
∴第2021个图形比第2020个图形多2021个三角形.
素养通关
14.【解析】(1)3;5;7;13.
提示:图②有3个三角形;图③有5个三角形;图④有7个三角形;…;猜测第七个图形中有13个三角形.
(2)(2n-1).
提示:∵图②有3个三角形,3=2×2-1;
图③有5个三角形,5=2×3-1;
图④有7个三角形,7=2×4-1;
∴第n个图形中有(2n-1)个三角形.
15.【解析】(1)∵(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,∴a=b=c,
∴△ABC是等边三角形.
(2)∵a=5,b=2,且c为整数,
∴5-2
当c=4时,△ABC周长的最小值=5+2+4=11;
当c=6时,△ABC周长的最大值=5+2+6=13.
2
