13.1 课时3 三角形中几条重要线段 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 13.1 课时3 三角形中几条重要线段 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 217.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览


文档简介
13.1 课时3 三角形中几条重要线段
【练基础】
必备知识1 三角形的高线
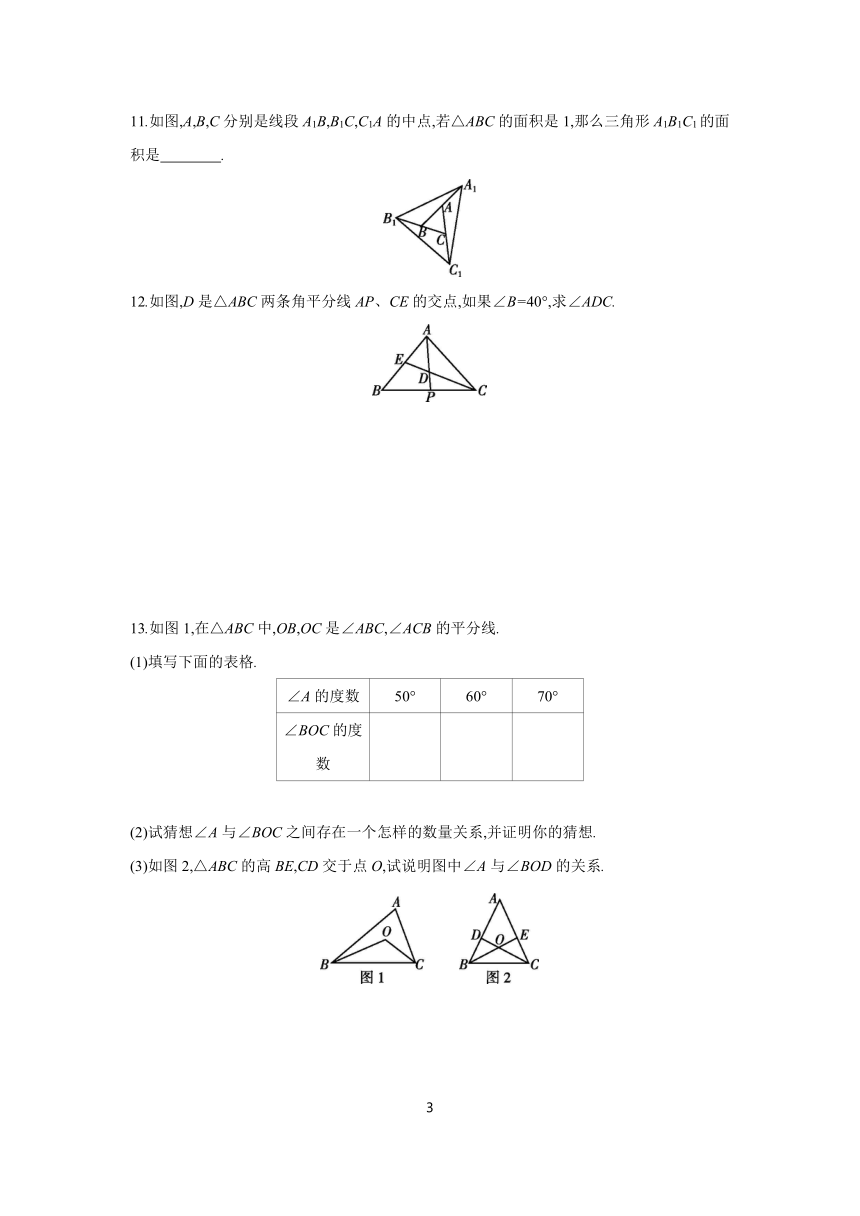
1.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是 ( )
A B C D
2.下列四个图形中,线段BE是△ABC的高的是 ( )
A B
C D
3.如图,在△ABC中,BC边上的高为 ( )
A.AD B.BE C.BF D.CG
4.【全椒期末】已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数.
必备知识2 三角形的中线
5.若AD是△ABC的中线,则下列结论正确的是 ( )
A.AD⊥BC B.BD=CD
C.∠BAD=∠CAD D.AD=BC
6.如图,AD是△ABC的中线,CO是△ACD的中线,△ABC的面积为10.则△COD的面积是 .
必备知识3 三角形高线与角平分线的综合
7.如图,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为 .
8.如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
【练能力】
9.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法错误的是 ( )
A.BF=CF
B.∠C+∠CAD=90°
C.∠BAF=∠CAF
D.S△ABC=2S△ABF
10.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点H,则∠CHD= .
11.如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么三角形A1B1C1的面积是 .
12.如图,D是△ABC两条角平分线AP、CE的交点,如果∠B=40°,求∠ADC.
13.如图1,在△ABC中,OB,OC是∠ABC,∠ACB的平分线.
(1)填写下面的表格.
∠A的度数 50° 60° 70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想.
(3)如图2,△ABC的高BE,CD交于点O,试说明图中∠A与∠BOD的关系.
【练素养】
14.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数.
(2)求∠DAE的度数.
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数吗 若能,请你写出求解过程;若不能,请说明理由.
参考答案
基础演练
1.B 2.C 3.A
4.【解析】①如图1,当高AD在△ABC的内部时,
∠BAC=∠BAD+∠CAD=70°+20°=90°;
②如图2,当高AD在△ABC的外部时,
∠BAC=∠BAD-∠CAD=70°-20°=50°.
综上所述,∠BAC的度数为90°或50°.
5.B 6.2.5 7.85°
8.【解析】∵CD⊥AB,∴∠CDB=90°.
∵∠B=60°,
∴∠BCD=180°-90°-∠B=90°-60°=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=50°,
∴∠AEC=180°-∠A-∠ACE=110°,
∴∠CEB=180°-∠AEC=70°,
∠ECD=180°-90°-70°=20°.
能力生成
9.C 10.45° 11.7
12.【解析】∵∠B=40°,∠B+∠BAC+∠BCA=180°,
∴∠BAC+∠BCA=140°.
∵CE,AP分别平分∠ACB和∠BAC,
∴∠CAP=∠BAC,
∠ACE=∠BCA.
∵∠BAC+∠BCA=140°,
∴∠CAP+∠ACE=70°,
∴∠ADC=180°-(∠CAP+∠ACE)=180°-70°=110°.
13.【解析】(1)115°;120°;125°.
(2)猜想:∠BOC=90°+∠A.
理由:∵在△ABC中,OB,OC是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB.
∵∠ABC+∠ACB=180°-∠A,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°-∠A=90°+∠A.
(3)∵△ABC的高BE,CD交于点O,
∴∠BDC=∠BEA=90°,
∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,
∴∠A=∠BOD.
素养通关
14.【解析】(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°.
(2)∵AD⊥BC,
∴∠ADE=90°.
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-70°=20°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°.
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C.
∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C).
∵AD⊥BC,
∴∠ADE=90°.
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-(∠B+∠C)-(90°-∠B)=(∠B-∠C).
∵∠B-∠C=40°,
∴∠DAE=×40°=20°.
2
【练基础】
必备知识1 三角形的高线
1.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是 ( )
A B C D
2.下列四个图形中,线段BE是△ABC的高的是 ( )
A B
C D
3.如图,在△ABC中,BC边上的高为 ( )
A.AD B.BE C.BF D.CG
4.【全椒期末】已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数.
必备知识2 三角形的中线
5.若AD是△ABC的中线,则下列结论正确的是 ( )
A.AD⊥BC B.BD=CD
C.∠BAD=∠CAD D.AD=BC
6.如图,AD是△ABC的中线,CO是△ACD的中线,△ABC的面积为10.则△COD的面积是 .
必备知识3 三角形高线与角平分线的综合
7.如图,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为 .
8.如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
【练能力】
9.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法错误的是 ( )
A.BF=CF
B.∠C+∠CAD=90°
C.∠BAF=∠CAF
D.S△ABC=2S△ABF
10.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点H,则∠CHD= .
11.如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么三角形A1B1C1的面积是 .
12.如图,D是△ABC两条角平分线AP、CE的交点,如果∠B=40°,求∠ADC.
13.如图1,在△ABC中,OB,OC是∠ABC,∠ACB的平分线.
(1)填写下面的表格.
∠A的度数 50° 60° 70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想.
(3)如图2,△ABC的高BE,CD交于点O,试说明图中∠A与∠BOD的关系.
【练素养】
14.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数.
(2)求∠DAE的度数.
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数吗 若能,请你写出求解过程;若不能,请说明理由.
参考答案
基础演练
1.B 2.C 3.A
4.【解析】①如图1,当高AD在△ABC的内部时,
∠BAC=∠BAD+∠CAD=70°+20°=90°;
②如图2,当高AD在△ABC的外部时,
∠BAC=∠BAD-∠CAD=70°-20°=50°.
综上所述,∠BAC的度数为90°或50°.
5.B 6.2.5 7.85°
8.【解析】∵CD⊥AB,∴∠CDB=90°.
∵∠B=60°,
∴∠BCD=180°-90°-∠B=90°-60°=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=50°,
∴∠AEC=180°-∠A-∠ACE=110°,
∴∠CEB=180°-∠AEC=70°,
∠ECD=180°-90°-70°=20°.
能力生成
9.C 10.45° 11.7
12.【解析】∵∠B=40°,∠B+∠BAC+∠BCA=180°,
∴∠BAC+∠BCA=140°.
∵CE,AP分别平分∠ACB和∠BAC,
∴∠CAP=∠BAC,
∠ACE=∠BCA.
∵∠BAC+∠BCA=140°,
∴∠CAP+∠ACE=70°,
∴∠ADC=180°-(∠CAP+∠ACE)=180°-70°=110°.
13.【解析】(1)115°;120°;125°.
(2)猜想:∠BOC=90°+∠A.
理由:∵在△ABC中,OB,OC是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB.
∵∠ABC+∠ACB=180°-∠A,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°-∠A=90°+∠A.
(3)∵△ABC的高BE,CD交于点O,
∴∠BDC=∠BEA=90°,
∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,
∴∠A=∠BOD.
素养通关
14.【解析】(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°.
(2)∵AD⊥BC,
∴∠ADE=90°.
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-70°=20°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°.
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C.
∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C).
∵AD⊥BC,
∴∠ADE=90°.
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-(∠B+∠C)-(90°-∠B)=(∠B-∠C).
∵∠B-∠C=40°,
∴∠DAE=×40°=20°.
2
