13.2 课时4 三角形内角和定理的推论——三角形外角的性质 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 13.2 课时4 三角形内角和定理的推论——三角形外角的性质 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 242.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:07:38 | ||
图片预览


文档简介
13.2 课时4 三角形内角和定理的推论——三角形外角的性质
【练基础】
必备知识1 三角形外角的定义
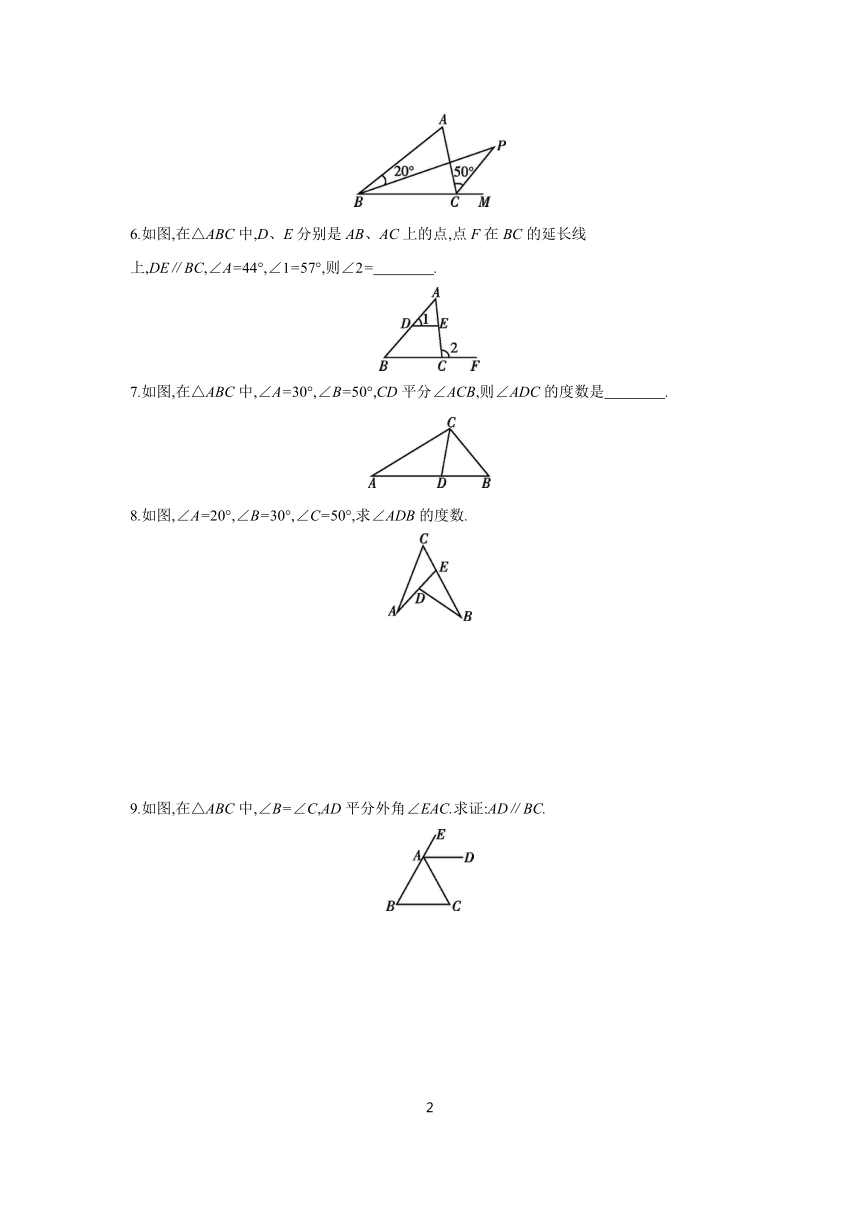
1.如图,下列各角是△ABC的外角的是 ( )
A.∠4
B.∠3
C.∠2
D.∠1
必备知识2 三角形外角的性质1
2.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A.50° B.30° C.20° D.15°
3.三角形的一个外角小于与它相邻的内角,这个三角形是 ( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不确定
4.如图,已知D,B,C,E四点共线,∠ABD+∠ACE=230°,则∠A的度数为 ( )
A.50° B.60° C.70° D.80°
5.如图,在△ABC中,BP平分∠ABC,CP是∠ACB的外角的平分线,若∠ABP=20°,∠ACP=50°,则∠A= ( )
A.60° B.80° C.70° D.50°
6.如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2= .
7.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是 .
8.如图,∠A=20°,∠B=30°,∠C=50°,求∠ADB的度数.
9.如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.求证:AD∥BC.
必备知识3 三角形外角的性质2
10.在下列四个图形中,∠2>∠1一定成立的是 ( )
A B C D
【练能力】
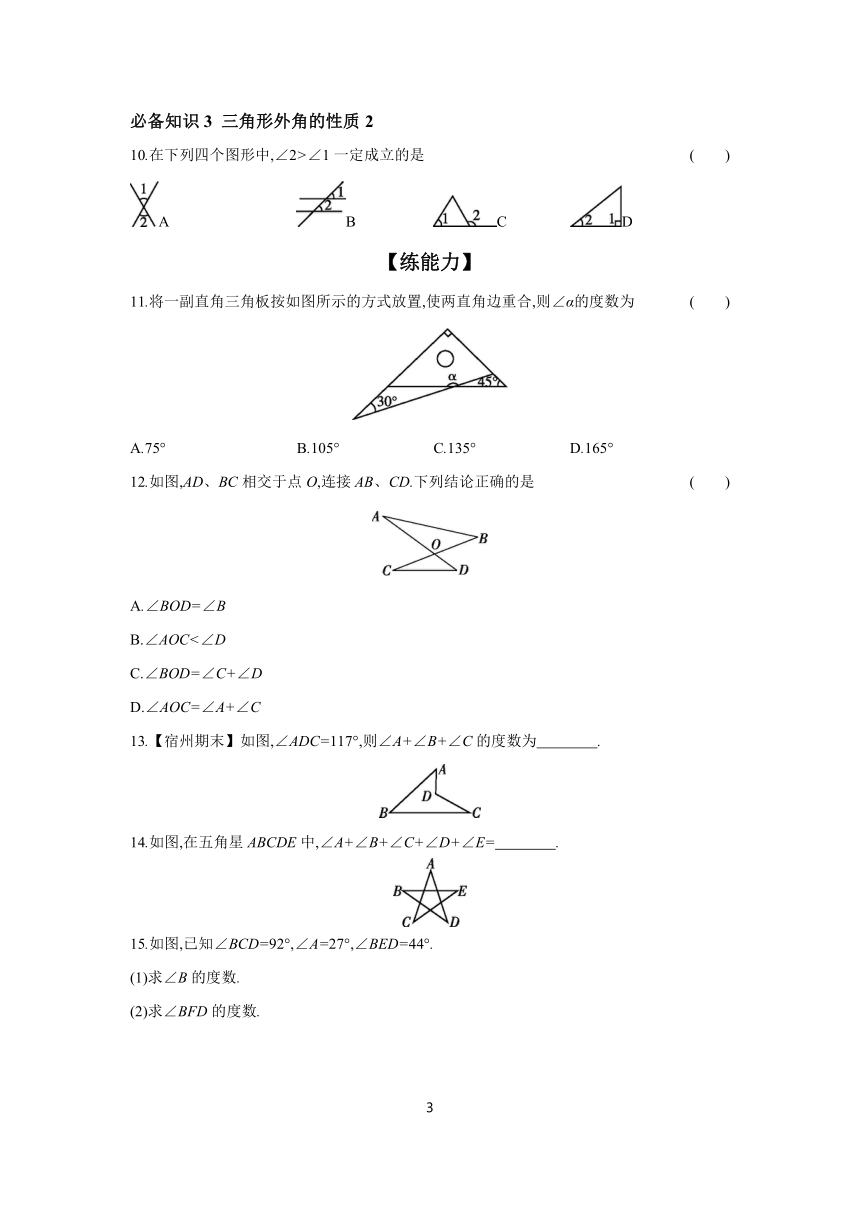
11.将一副直角三角板按如图所示的方式放置,使两直角边重合,则∠α的度数为 ( )
A.75° B.105° C.135° D.165°
12.如图,AD、BC相交于点O,连接AB、CD.下列结论正确的是 ( )
A.∠BOD=∠B
B.∠AOC<∠D
C.∠BOD=∠C+∠D
D.∠AOC=∠A+∠C
13.【宿州期末】如图,∠ADC=117°,则∠A+∠B+∠C的度数为 .
14.如图,在五角星ABCDE中,∠A+∠B+∠C+∠D+∠E= .
15.如图,已知∠BCD=92°,∠A=27°,∠BED=44°.
(1)求∠B的度数.
(2)求∠BFD的度数.
16.如图,将△ABC折叠,使点C落在点C'处,折痕为EF.
(1)若∠1=40°,∠2=20°,求∠C的度数.
(2)探究∠1,∠2与∠C之间的数量关系.
【练素养】
17.如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数.
(2)如图2,作△ABC外角∠MBC,∠NCB的平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图3,延长线段BP、QC交于点E,在△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
基础演练
1.B 2.C 3.B 4.A 5.A 6.101° 7.100°
8.【解析】∵∠AEB是△ACE的一个外角,
∴∠AEB=∠A+∠C=20°+50°=70°.
∵∠ADB是△DEB的一个外角,
∴∠ADB=∠AEB+∠B=70°+30°=100°.
9.【解析】证明:由三角形的外角性质可知,∠EAC=∠B+∠C.
∵∠B=∠C,∴∠EAC=2∠B.
∵AD平分外角∠EAC,∴∠EAC=2∠EAD,
∴∠B=∠EAD,
∴AD∥BC.
10.C
能力生成
11.D 12.C 13.117° 14.180°
15.【解析】(1)∵∠BCD=∠A+∠B,∠BCD=92°,∠A=27°,
∴∠B=∠BCD-∠A=92°-27°=65°.
(2)∵∠BFD=∠B+∠BED,∠BED=44°,∠B=65°,∴∠BFD=44°+65°=109°.
16.【解析】(1)∵∠1=40°,∠2=20°,
∴∠CEC'=180°-∠1=180°-40°=140°,
∠CFC'=180°-∠2=180°-20°=160°.
由翻折的性质得∠CEF=∠CEC'=×140°=70°,∠CFE=∠CFC'=×160°=80°.
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-70°-80°=30°.
(2)∠CEC'=180°-∠1,∠CFC'=180°-∠2.
由翻折的性质得∠CEF=∠CEC',∠CFE=∠CFC'.
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-(180°-∠1)-(180°-∠2)=(∠1+∠2),∴∠1+∠2=2∠C.
素养通关
17.【解析】(1)∵∠A=80°,
∴∠ABC+∠ACB=100°.
∵P是∠ABC的平分线和∠ACB的平分线的交点,
∴∠BPC=180°-(∠ABC+∠ACB)=180°-×100°=130°.
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°-∠ABC-∠ACB)
=(180°+∠A)
=90°+∠A,
∴∠Q=180°-90°+∠A=90°-∠A.
(3)如图,延长BC至点F.
∵CQ为△ABC的外角∠NCB的平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF.
∵BE平分∠ABC,
∴∠ABC=2∠EBC.
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E.
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A.
由题意得∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠MBC)=90°.
如果在△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=290°-∠A,解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
2
【练基础】
必备知识1 三角形外角的定义
1.如图,下列各角是△ABC的外角的是 ( )
A.∠4
B.∠3
C.∠2
D.∠1
必备知识2 三角形外角的性质1
2.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A.50° B.30° C.20° D.15°
3.三角形的一个外角小于与它相邻的内角,这个三角形是 ( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不确定
4.如图,已知D,B,C,E四点共线,∠ABD+∠ACE=230°,则∠A的度数为 ( )
A.50° B.60° C.70° D.80°
5.如图,在△ABC中,BP平分∠ABC,CP是∠ACB的外角的平分线,若∠ABP=20°,∠ACP=50°,则∠A= ( )
A.60° B.80° C.70° D.50°
6.如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2= .
7.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是 .
8.如图,∠A=20°,∠B=30°,∠C=50°,求∠ADB的度数.
9.如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.求证:AD∥BC.
必备知识3 三角形外角的性质2
10.在下列四个图形中,∠2>∠1一定成立的是 ( )
A B C D
【练能力】
11.将一副直角三角板按如图所示的方式放置,使两直角边重合,则∠α的度数为 ( )
A.75° B.105° C.135° D.165°
12.如图,AD、BC相交于点O,连接AB、CD.下列结论正确的是 ( )
A.∠BOD=∠B
B.∠AOC<∠D
C.∠BOD=∠C+∠D
D.∠AOC=∠A+∠C
13.【宿州期末】如图,∠ADC=117°,则∠A+∠B+∠C的度数为 .
14.如图,在五角星ABCDE中,∠A+∠B+∠C+∠D+∠E= .
15.如图,已知∠BCD=92°,∠A=27°,∠BED=44°.
(1)求∠B的度数.
(2)求∠BFD的度数.
16.如图,将△ABC折叠,使点C落在点C'处,折痕为EF.
(1)若∠1=40°,∠2=20°,求∠C的度数.
(2)探究∠1,∠2与∠C之间的数量关系.
【练素养】
17.如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数.
(2)如图2,作△ABC外角∠MBC,∠NCB的平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图3,延长线段BP、QC交于点E,在△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
基础演练
1.B 2.C 3.B 4.A 5.A 6.101° 7.100°
8.【解析】∵∠AEB是△ACE的一个外角,
∴∠AEB=∠A+∠C=20°+50°=70°.
∵∠ADB是△DEB的一个外角,
∴∠ADB=∠AEB+∠B=70°+30°=100°.
9.【解析】证明:由三角形的外角性质可知,∠EAC=∠B+∠C.
∵∠B=∠C,∴∠EAC=2∠B.
∵AD平分外角∠EAC,∴∠EAC=2∠EAD,
∴∠B=∠EAD,
∴AD∥BC.
10.C
能力生成
11.D 12.C 13.117° 14.180°
15.【解析】(1)∵∠BCD=∠A+∠B,∠BCD=92°,∠A=27°,
∴∠B=∠BCD-∠A=92°-27°=65°.
(2)∵∠BFD=∠B+∠BED,∠BED=44°,∠B=65°,∴∠BFD=44°+65°=109°.
16.【解析】(1)∵∠1=40°,∠2=20°,
∴∠CEC'=180°-∠1=180°-40°=140°,
∠CFC'=180°-∠2=180°-20°=160°.
由翻折的性质得∠CEF=∠CEC'=×140°=70°,∠CFE=∠CFC'=×160°=80°.
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-70°-80°=30°.
(2)∠CEC'=180°-∠1,∠CFC'=180°-∠2.
由翻折的性质得∠CEF=∠CEC',∠CFE=∠CFC'.
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-(180°-∠1)-(180°-∠2)=(∠1+∠2),∴∠1+∠2=2∠C.
素养通关
17.【解析】(1)∵∠A=80°,
∴∠ABC+∠ACB=100°.
∵P是∠ABC的平分线和∠ACB的平分线的交点,
∴∠BPC=180°-(∠ABC+∠ACB)=180°-×100°=130°.
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°-∠ABC-∠ACB)
=(180°+∠A)
=90°+∠A,
∴∠Q=180°-90°+∠A=90°-∠A.
(3)如图,延长BC至点F.
∵CQ为△ABC的外角∠NCB的平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF.
∵BE平分∠ABC,
∴∠ABC=2∠EBC.
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E.
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A.
由题意得∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠MBC)=90°.
如果在△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=290°-∠A,解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
2
