14.1 全等三角形 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 14.1 全等三角形 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 238.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:08:24 | ||
图片预览


文档简介
14.1 全等三角形
【练基础】
必备知识1 认识全等形
1.下列说法中,正确的是 ( )
A.面积相等的两个图形是全等图形
B.形状相等的两个图形是全等图形
C.周长相等的两个图形是全等图形
D.能够完全重合的两个图形是全等图形
2.下列各组中的两个图形属于全等图形的是 ( )
A B C D
必备知识2 全等三角形及对应元素
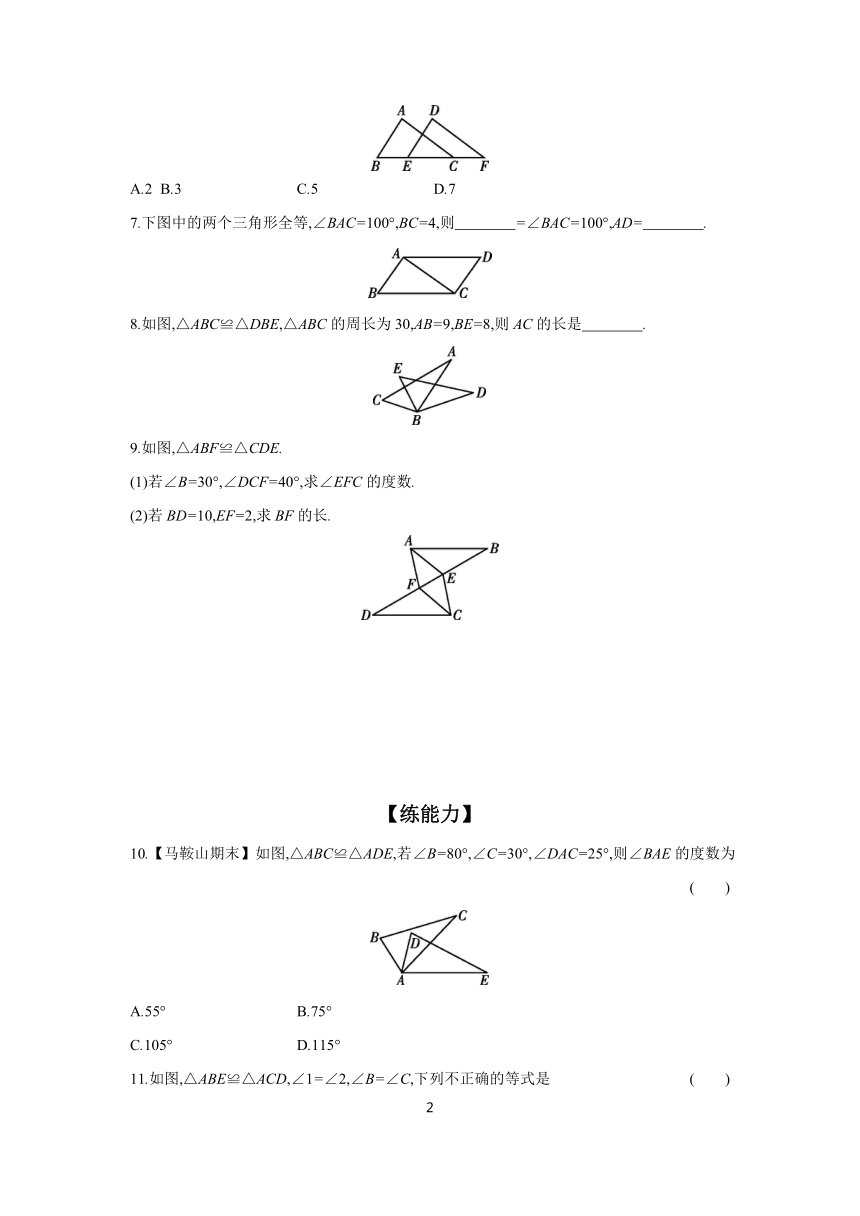
3.如图,△ABN≌△ACM,∠B和∠C是对应角,AB和AC是对应边,那么∠BAN的对应角是 ,∠ANB的对应角是 ,AN的对应边是 ,BN的对应边是 .
必备知识3 全等三角形的性质
4.如图,图中的两个三角形全等,则∠α的度数为 ( )
A.71° B.59° C.58° D.50°
5.如图,△ABC≌△DEC,点B、C、D在同一直线上,且CE=2 cm,CD=4 cm,则BD的长为 ( )
A.1.5 cm B.2 cm C.4.5 cm D.6 cm
6.如图,若△ABC≌△DEF,点B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2 B.3 C.5 D.7
7.下图中的两个三角形全等,∠BAC=100°,BC=4,则 =∠BAC=100°,AD= .
8.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
9.如图,△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数.
(2)若BD=10,EF=2,求BF的长.
【练能力】
10.【马鞍山期末】如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=25°,则∠BAE的度数为 ( )
A.55° B.75°
C.105° D.115°
11.如图,△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是 ( )
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
12.如图,两个直角三角形,若△ABC≌△CDE,则线段AC和线段CE的关系是 ( )
A.既不相等也不互相垂直
B.相等但不互相垂直
C.互相垂直但不相等
D.相等且互相垂直
13.如图,图形的各个顶点都在3×3正方形方格的格点上,则∠1+∠2= ( )
A.60° B.72°
C.45° D.90°
14.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限,且△ABD与△ABC全等,则点D的坐标是 .
15.【安徽月考】如图,△ABC≌△ADE,点E在边BC上.求证:∠BED=∠BAD.
16.如图,点A、B、C、D在同一条直线上,E、F是直线AD上方的点,连接AE、CE、BF、DF,若△ACE≌△FDB,FD=3,AD=8.
(1)判断直线CE与DF是否平行 并说明理由.
(2)求CD的长.
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
【练素养】
17.如图,A,C,E三点在同一条直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE.
(2)当△ABC满足什么条件时,BC∥DE
参考答案
基础演练
1.D 2.B 3.∠CAM ∠AMC AM CM
4.B 5.D 6.B 7.∠ACD 4 8.13
9.【解析】(1)∵△ABF≌△CDE,∴∠D=∠B=30°,
∴∠EFC=∠DCF+∠D=70°.
(2)∵△ABF≌△CDE,
∴BF=DE,∴BF-EF=DE-EF,
即BE=DF.
∵BD=10,EF=2,
∴BE=(10-2)÷2=4,∴BF=BE+EF=6.
能力生成
10.D 11.D 12.D 13.C
14.(-4,3)或(-4,2)
15.【解析】证明:∵△ABC≌△ADE,
∴∠C=∠AED,∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠CAE=∠BAD.
∵∠AEB=∠AED+∠DEB=∠CAE+∠C,
∴∠CAE=∠BED,∴∠BED=∠BAD.
16.【解析】(1)CE∥DF.
理由:∵△ACE≌△FDB,
∴∠ACE=∠D,∴CE∥DF.
(2)∵△ACE≌△FDB,∴AC=DF=3.
∵AD=8,∴CD=AD-AC=8-3=5.
(3)如图,∵△ACE≌△FDB,∴∠DBF=∠E=26°.
∵CE∥DF,∴∠1=∠F=53°,
∴∠ACE=180°-26°-53°=101°.
素养通关
17.【解析】(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE.
又∵AE=AC+CE,∴BC=DE+CE.
(2)若BC∥DE,则∠BCE=∠E.
又∵△ABC≌△DAE,
∴∠ACB=∠E,∴∠ACB=∠BCE.
又∵∠ACB+∠BCE=180°,∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
2
【练基础】
必备知识1 认识全等形
1.下列说法中,正确的是 ( )
A.面积相等的两个图形是全等图形
B.形状相等的两个图形是全等图形
C.周长相等的两个图形是全等图形
D.能够完全重合的两个图形是全等图形
2.下列各组中的两个图形属于全等图形的是 ( )
A B C D
必备知识2 全等三角形及对应元素
3.如图,△ABN≌△ACM,∠B和∠C是对应角,AB和AC是对应边,那么∠BAN的对应角是 ,∠ANB的对应角是 ,AN的对应边是 ,BN的对应边是 .
必备知识3 全等三角形的性质
4.如图,图中的两个三角形全等,则∠α的度数为 ( )
A.71° B.59° C.58° D.50°
5.如图,△ABC≌△DEC,点B、C、D在同一直线上,且CE=2 cm,CD=4 cm,则BD的长为 ( )
A.1.5 cm B.2 cm C.4.5 cm D.6 cm
6.如图,若△ABC≌△DEF,点B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2 B.3 C.5 D.7
7.下图中的两个三角形全等,∠BAC=100°,BC=4,则 =∠BAC=100°,AD= .
8.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
9.如图,△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数.
(2)若BD=10,EF=2,求BF的长.
【练能力】
10.【马鞍山期末】如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=25°,则∠BAE的度数为 ( )
A.55° B.75°
C.105° D.115°
11.如图,△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是 ( )
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
12.如图,两个直角三角形,若△ABC≌△CDE,则线段AC和线段CE的关系是 ( )
A.既不相等也不互相垂直
B.相等但不互相垂直
C.互相垂直但不相等
D.相等且互相垂直
13.如图,图形的各个顶点都在3×3正方形方格的格点上,则∠1+∠2= ( )
A.60° B.72°
C.45° D.90°
14.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限,且△ABD与△ABC全等,则点D的坐标是 .
15.【安徽月考】如图,△ABC≌△ADE,点E在边BC上.求证:∠BED=∠BAD.
16.如图,点A、B、C、D在同一条直线上,E、F是直线AD上方的点,连接AE、CE、BF、DF,若△ACE≌△FDB,FD=3,AD=8.
(1)判断直线CE与DF是否平行 并说明理由.
(2)求CD的长.
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
【练素养】
17.如图,A,C,E三点在同一条直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE.
(2)当△ABC满足什么条件时,BC∥DE
参考答案
基础演练
1.D 2.B 3.∠CAM ∠AMC AM CM
4.B 5.D 6.B 7.∠ACD 4 8.13
9.【解析】(1)∵△ABF≌△CDE,∴∠D=∠B=30°,
∴∠EFC=∠DCF+∠D=70°.
(2)∵△ABF≌△CDE,
∴BF=DE,∴BF-EF=DE-EF,
即BE=DF.
∵BD=10,EF=2,
∴BE=(10-2)÷2=4,∴BF=BE+EF=6.
能力生成
10.D 11.D 12.D 13.C
14.(-4,3)或(-4,2)
15.【解析】证明:∵△ABC≌△ADE,
∴∠C=∠AED,∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠CAE=∠BAD.
∵∠AEB=∠AED+∠DEB=∠CAE+∠C,
∴∠CAE=∠BED,∴∠BED=∠BAD.
16.【解析】(1)CE∥DF.
理由:∵△ACE≌△FDB,
∴∠ACE=∠D,∴CE∥DF.
(2)∵△ACE≌△FDB,∴AC=DF=3.
∵AD=8,∴CD=AD-AC=8-3=5.
(3)如图,∵△ACE≌△FDB,∴∠DBF=∠E=26°.
∵CE∥DF,∴∠1=∠F=53°,
∴∠ACE=180°-26°-53°=101°.
素养通关
17.【解析】(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE.
又∵AE=AC+CE,∴BC=DE+CE.
(2)若BC∥DE,则∠BCE=∠E.
又∵△ABC≌△DAE,
∴∠ACB=∠E,∴∠ACB=∠BCE.
又∵∠ACB+∠BCE=180°,∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
2
