14.2 课时2 两角及其夹边分别相等的两个三角形 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 14.2 课时2 两角及其夹边分别相等的两个三角形 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 209.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:28:44 | ||
图片预览

文档简介
14.2 课时2 两角及其夹边分别相等的两个三角形
【练基础】
必备知识1 用ASA判定三角形全等
1.能判定△ABC≌△DEF的条件是 ( )
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D
D.∠A=∠D,AB=DE,∠B=∠E
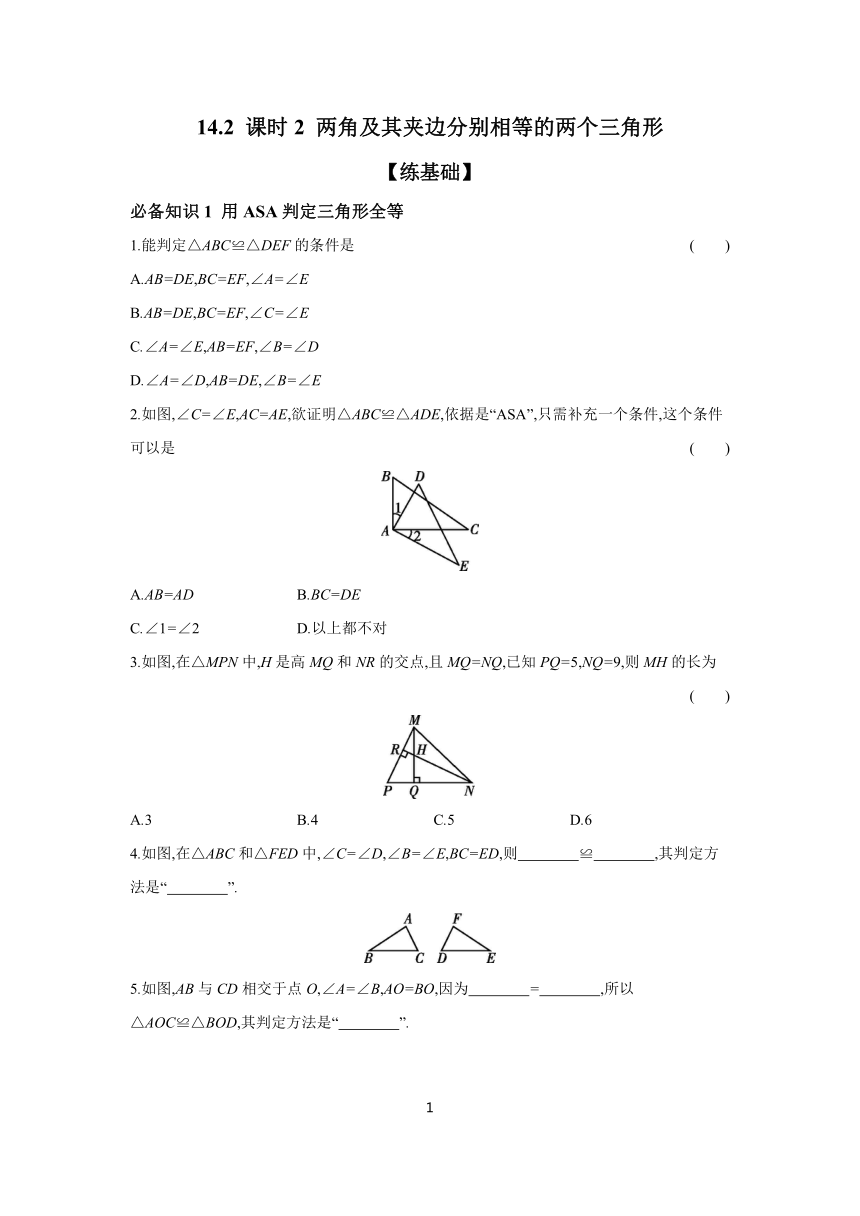
2.如图,∠C=∠E,AC=AE,欲证明△ABC≌△ADE,依据是“ASA”,只需补充一个条件,这个条件可以是 ( )
A.AB=AD B.BC=DE
C.∠1=∠2 D.以上都不对
3.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为 ( )
A.3 B.4 C.5 D.6
4.如图,在△ABC和△FED中,∠C=∠D,∠B=∠E,BC=ED,则 ≌ ,其判定方法是“ ”.
5.如图,AB与CD相交于点O,∠A=∠B,AO=BO,因为 = ,所以△AOC≌△BOD,其判定方法是“ ”.
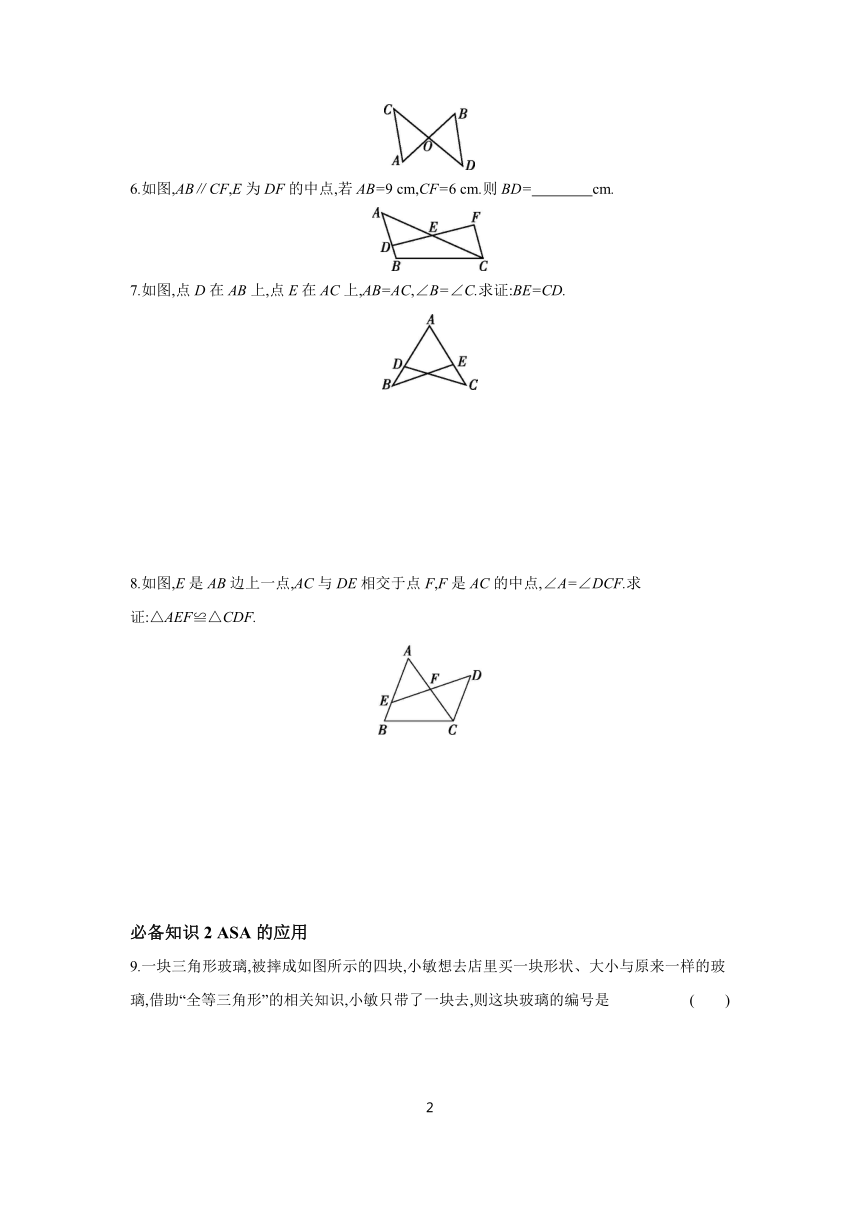
6.如图,AB∥CF,E为DF的中点,若AB=9 cm,CF=6 cm.则BD= cm.
7.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BE=CD.
8.如图,E是AB边上一点,AC与DE相交于点F,F是AC的中点,∠A=∠DCF.求证:△AEF≌△CDF.
必备知识2 ASA的应用
9.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是 ( )
A.① B.② C.③ D.④
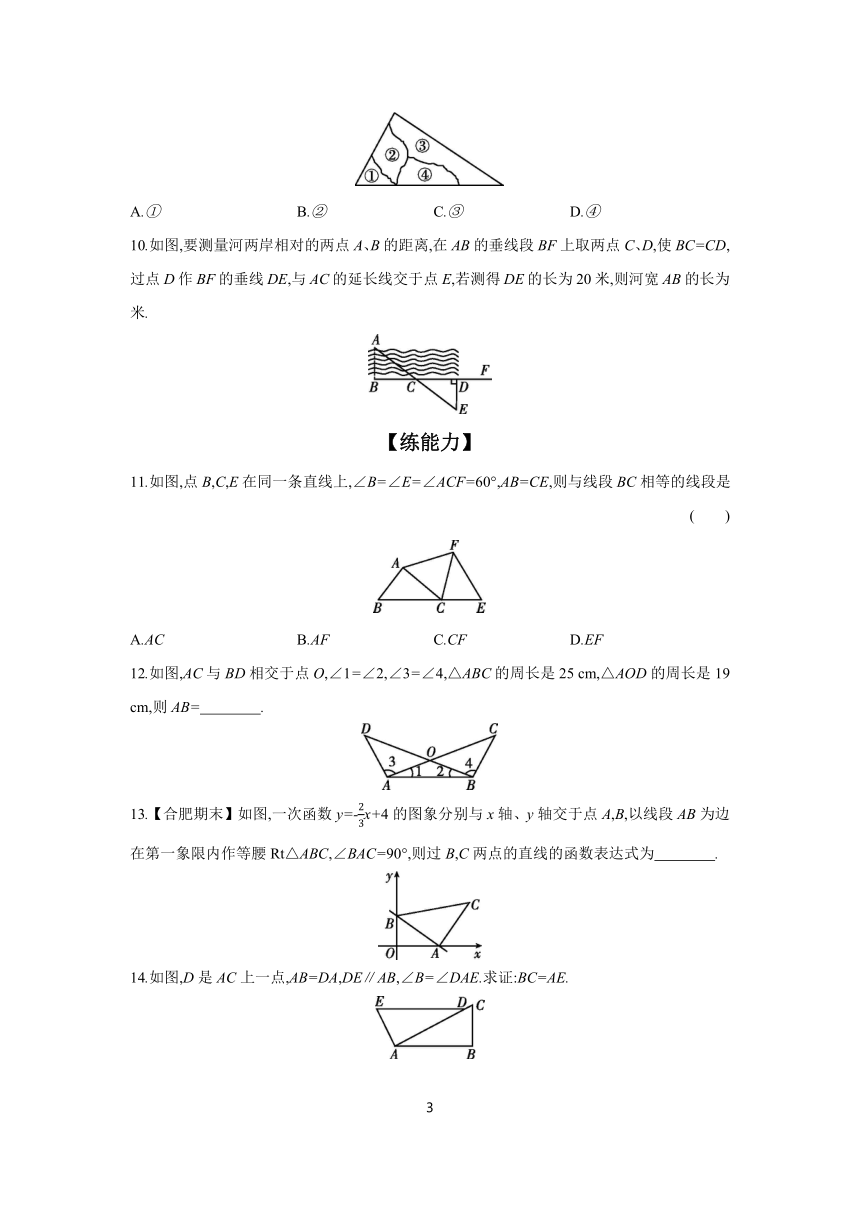
10.如图,要测量河两岸相对的两点A、B的距离,在AB的垂线段BF上取两点C、D,使BC=CD,过点D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为20米,则河宽AB的长为 米.
【练能力】
11.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是 ( )
A.AC B.AF C.CF D.EF
12.如图,AC与BD相交于点O,∠1=∠2,∠3=∠4,△ABC的周长是25 cm,△AOD的周长是19 cm,则AB= .
13.【合肥期末】如图,一次函数y=-x+4的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B,C两点的直线的函数表达式为 .
14.如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.
15.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
16.如图,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9 cm,AN=2 cm,求△ABC的周长.
【练素养】
17.如图,要测量湖中小岛E距岸边A和D的距离,方法如下:(1)任作线段AB,取AB的中点O;(2)连接DO并延长使CO=DO;(3)连接BC;(4)用仪器测量使点E,O,F在一条直线上,并交CB于点F,要测量AE,DE的长度,只需测量出BF,CF的长度即可,为什么
参考答案
基础演练
1.D 2.C 3.B 4.△ABC △FED ASA
5.∠AOC ∠BOD ASA 6.3
7.【解析】证明:在△ABE与△ACD中,
∴△ABE≌△ACD(ASA),
∴BE=CD.
8.【解析】证明:∵F是AC的中点,
∴AF=CF.
在△AEF和△CDF中,
∴△AEF≌△CDF(ASA).
9.C 10.20 11.D 12.6 cm 13.y=x+4
14.【解析】证明:∵DE∥AB,∴∠CAB=∠ADE.
在△ABC与△DAE中,
∴△ABC≌△DAE(ASA),∴BC=AE.
15.【解析】证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
∴△ADB≌△AEC(ASA),∴AB=AC.
又∵AD=AE,∴AB-AE=AC-AD,
即BE=CD.
16.【解析】∵MN平分∠AMC,
∴∠AMN=∠CMN.
∵MN⊥AC,
∴∠MNC=∠MNA=90°.
在△AMN和△CMN中,
∴△AMN≌△CMN(ASA),
∴AN=CN,AM=CM.
∵AN=2 cm,∴AC=2×2=4 cm.
∵AB+BM+AM=9 cm,
∴AB+BM+CM=AB+BC=9 cm,
∴AB+BC+AC=9+4=13 cm,
即△ABC的周长为13 cm.
素养通关
17.【解析】由作法可知,在△AOD与△BOC中,
∴△AOD≌△BOC(SAS),
∴AD=BC,∠A=∠B.
在△AOE与△BOF中,
∴△AOE≌△BOF(ASA),
∴AE=BF,∴AD-AE=BC-BF,
即DE=CF.
因此只要测出BF,CF的长度,即可知道AE,DE的长度了.
2
【练基础】
必备知识1 用ASA判定三角形全等
1.能判定△ABC≌△DEF的条件是 ( )
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D
D.∠A=∠D,AB=DE,∠B=∠E
2.如图,∠C=∠E,AC=AE,欲证明△ABC≌△ADE,依据是“ASA”,只需补充一个条件,这个条件可以是 ( )
A.AB=AD B.BC=DE
C.∠1=∠2 D.以上都不对
3.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为 ( )
A.3 B.4 C.5 D.6
4.如图,在△ABC和△FED中,∠C=∠D,∠B=∠E,BC=ED,则 ≌ ,其判定方法是“ ”.
5.如图,AB与CD相交于点O,∠A=∠B,AO=BO,因为 = ,所以△AOC≌△BOD,其判定方法是“ ”.
6.如图,AB∥CF,E为DF的中点,若AB=9 cm,CF=6 cm.则BD= cm.
7.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BE=CD.
8.如图,E是AB边上一点,AC与DE相交于点F,F是AC的中点,∠A=∠DCF.求证:△AEF≌△CDF.
必备知识2 ASA的应用
9.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是 ( )
A.① B.② C.③ D.④
10.如图,要测量河两岸相对的两点A、B的距离,在AB的垂线段BF上取两点C、D,使BC=CD,过点D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为20米,则河宽AB的长为 米.
【练能力】
11.如图,点B,C,E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则与线段BC相等的线段是 ( )
A.AC B.AF C.CF D.EF
12.如图,AC与BD相交于点O,∠1=∠2,∠3=∠4,△ABC的周长是25 cm,△AOD的周长是19 cm,则AB= .
13.【合肥期末】如图,一次函数y=-x+4的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B,C两点的直线的函数表达式为 .
14.如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.
15.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
16.如图,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9 cm,AN=2 cm,求△ABC的周长.
【练素养】
17.如图,要测量湖中小岛E距岸边A和D的距离,方法如下:(1)任作线段AB,取AB的中点O;(2)连接DO并延长使CO=DO;(3)连接BC;(4)用仪器测量使点E,O,F在一条直线上,并交CB于点F,要测量AE,DE的长度,只需测量出BF,CF的长度即可,为什么
参考答案
基础演练
1.D 2.C 3.B 4.△ABC △FED ASA
5.∠AOC ∠BOD ASA 6.3
7.【解析】证明:在△ABE与△ACD中,
∴△ABE≌△ACD(ASA),
∴BE=CD.
8.【解析】证明:∵F是AC的中点,
∴AF=CF.
在△AEF和△CDF中,
∴△AEF≌△CDF(ASA).
9.C 10.20 11.D 12.6 cm 13.y=x+4
14.【解析】证明:∵DE∥AB,∴∠CAB=∠ADE.
在△ABC与△DAE中,
∴△ABC≌△DAE(ASA),∴BC=AE.
15.【解析】证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
∴△ADB≌△AEC(ASA),∴AB=AC.
又∵AD=AE,∴AB-AE=AC-AD,
即BE=CD.
16.【解析】∵MN平分∠AMC,
∴∠AMN=∠CMN.
∵MN⊥AC,
∴∠MNC=∠MNA=90°.
在△AMN和△CMN中,
∴△AMN≌△CMN(ASA),
∴AN=CN,AM=CM.
∵AN=2 cm,∴AC=2×2=4 cm.
∵AB+BM+AM=9 cm,
∴AB+BM+CM=AB+BC=9 cm,
∴AB+BC+AC=9+4=13 cm,
即△ABC的周长为13 cm.
素养通关
17.【解析】由作法可知,在△AOD与△BOC中,
∴△AOD≌△BOC(SAS),
∴AD=BC,∠A=∠B.
在△AOE与△BOF中,
∴△AOE≌△BOF(ASA),
∴AE=BF,∴AD-AE=BC-BF,
即DE=CF.
因此只要测出BF,CF的长度,即可知道AE,DE的长度了.
2
