14.2 课时4 其他判定两个三角形全等的条件 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 14.2 课时4 其他判定两个三角形全等的条件 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
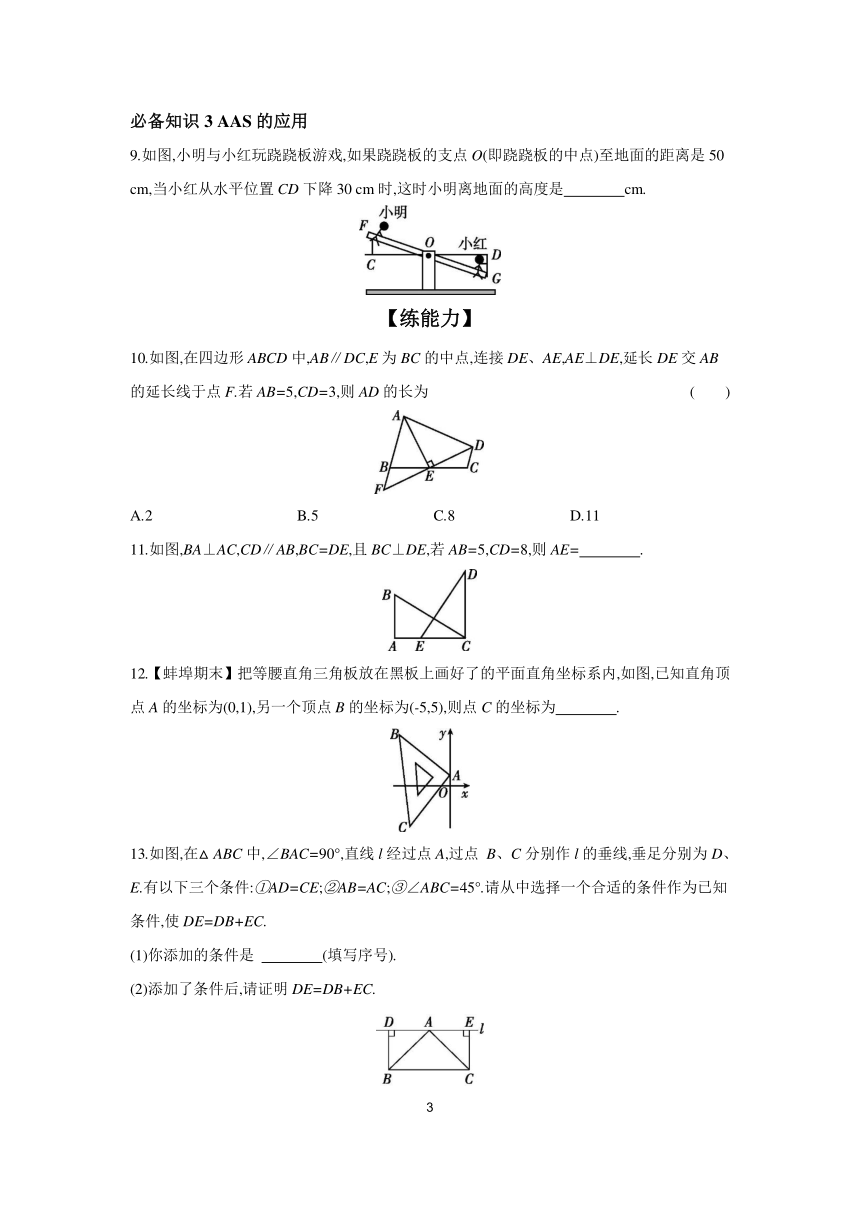
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:29:51 | ||
图片预览


文档简介
14.2 课时4 其他判定两个三角形全等的条件
【练基础】
必备知识1 SSA和AAA不能判定三角形全等
1.下列能够判定两个三角形全等的条件是 ( )
A.三个角对应相等
B.两条边和其中一边的对角对应相等
C.两个角对应相等
D.两个角和其中一角的对边对应相等
2.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
A.BD=CD
B.AB=AC
C.∠B=∠C
D.∠BDA=∠CDA
必备知识2 用AAS判定三角形全等
3.如图,∠1=∠2,BC=EC,请补充一个条件: ,能使用“AAS”方法判定△ABC≌△DEC.
4.如图,已知AE=AD,要直接利用AAS证明△ABE≌△ACD,应添加的条件是 .
5.如图,点A、D、B、F在同一条直线上,∠A=∠F,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)
6.【包河区期末】如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD= .
7.如图,在△ABC中,D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.求证:AD=ED.
8.如图,AB=AE,AB∥DE,∠ECB+∠D=180°.求证:AD=BC.
必备知识3 AAS的应用
9.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50 cm,当小红从水平位置CD下降30 cm时,这时小明离地面的高度是 cm.
【练能力】
10.如图,在四边形ABCD中,AB∥DC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为 ( )
A.2 B.5 C.8 D.11
11.如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE,若AB=5,CD=8,则AE= .
12.【蚌埠期末】把等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(-5,5),则点C的坐标为 .
13.如图,在△ABC中,∠BAC=90°,直线l经过点A,过点 B、C分别作l的垂线,垂足分别为D、E.有以下三个条件:①AD=CE;②AB=AC;③∠ABC=45°.请从中选择一个合适的条件作为已知条件,使DE=DB+EC.
(1)你添加的条件是 (填写序号).
(2)添加了条件后,请证明DE=DB+EC.
14.如图,在四边形ABCD中,AD∥BC,E为AC的中点,连接DE并延长,交BC于点F.
(1)求证:DE=EF.
(2)若AD=12,BF∶CF=2∶3,求BC的长.
【练素养】
15.【问题情境】如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,可知∠BAD=∠C(不需要证明).
【特例探究】如图2,∠MAN=90°,射线AE在这个角的内部,点B,C分别在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF.
【归纳证明】如图3,点B,C分别在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
【拓展应用】如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .
参考答案
基础演练
1.D 2.A 3.∠A=∠D 4.∠B=∠C
5.∠C=∠E或AC=FE或DE∥BC(答案不唯一)
6.1
7.【解析】证明:∵CE∥AB,∴∠BAD=∠E.
∵D是边BC的中点,
∴BD=CD.
在△ABD和△ECD中,
∴△ABD≌△ECD(AAS),∴AD=ED.
8.【解析】证明:∵AB∥DE,∴∠CAB=∠E.
∵∠ECB+∠D=180°,∠ECB+∠ACB=180°,
∴∠D=∠ACB.
在△ABC与△EAD中,
∴△ABC≌△EAD(AAS),∴AD=BC.
9.80 10.C 11.3 12.(-4,-4)
13.【解析】(1)①(答案不唯一).
(2)证明:∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE.
又∵AD=CE,
∴△BAD≌△ACE(AAS),
∴DB=EA,
∴DE=EA+AD=DB+EC.
14.【解析】(1)证明:∵AD∥BC,
∴∠DAE=∠FCE,∠ADE=∠EFC.
又∵E为AC的中点,∴AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).∴DE=EF.
(2)∵△ADE≌△CFE,∴AD=CF=12.
∵BF∶CF=2∶3,∴BF=8,
∴BC=BF+CF=8+12=20.
素养通关
15.【解析】【特例探究】∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠BAD+∠CAF=90°,
∴∠ABD=∠CAF.
在△ABD和△CAF中,
∴△ABD≌△CAF(AAS).
【归纳证明】∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF,∠AEB=∠CFA.
在△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
【拓展应用】5.
2
【练基础】
必备知识1 SSA和AAA不能判定三角形全等
1.下列能够判定两个三角形全等的条件是 ( )
A.三个角对应相等
B.两条边和其中一边的对角对应相等
C.两个角对应相等
D.两个角和其中一角的对边对应相等
2.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
A.BD=CD
B.AB=AC
C.∠B=∠C
D.∠BDA=∠CDA
必备知识2 用AAS判定三角形全等
3.如图,∠1=∠2,BC=EC,请补充一个条件: ,能使用“AAS”方法判定△ABC≌△DEC.
4.如图,已知AE=AD,要直接利用AAS证明△ABE≌△ACD,应添加的条件是 .
5.如图,点A、D、B、F在同一条直线上,∠A=∠F,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)
6.【包河区期末】如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD= .
7.如图,在△ABC中,D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.求证:AD=ED.
8.如图,AB=AE,AB∥DE,∠ECB+∠D=180°.求证:AD=BC.
必备知识3 AAS的应用
9.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50 cm,当小红从水平位置CD下降30 cm时,这时小明离地面的高度是 cm.
【练能力】
10.如图,在四边形ABCD中,AB∥DC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为 ( )
A.2 B.5 C.8 D.11
11.如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE,若AB=5,CD=8,则AE= .
12.【蚌埠期末】把等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(-5,5),则点C的坐标为 .
13.如图,在△ABC中,∠BAC=90°,直线l经过点A,过点 B、C分别作l的垂线,垂足分别为D、E.有以下三个条件:①AD=CE;②AB=AC;③∠ABC=45°.请从中选择一个合适的条件作为已知条件,使DE=DB+EC.
(1)你添加的条件是 (填写序号).
(2)添加了条件后,请证明DE=DB+EC.
14.如图,在四边形ABCD中,AD∥BC,E为AC的中点,连接DE并延长,交BC于点F.
(1)求证:DE=EF.
(2)若AD=12,BF∶CF=2∶3,求BC的长.
【练素养】
15.【问题情境】如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,可知∠BAD=∠C(不需要证明).
【特例探究】如图2,∠MAN=90°,射线AE在这个角的内部,点B,C分别在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF.
【归纳证明】如图3,点B,C分别在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
【拓展应用】如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .
参考答案
基础演练
1.D 2.A 3.∠A=∠D 4.∠B=∠C
5.∠C=∠E或AC=FE或DE∥BC(答案不唯一)
6.1
7.【解析】证明:∵CE∥AB,∴∠BAD=∠E.
∵D是边BC的中点,
∴BD=CD.
在△ABD和△ECD中,
∴△ABD≌△ECD(AAS),∴AD=ED.
8.【解析】证明:∵AB∥DE,∴∠CAB=∠E.
∵∠ECB+∠D=180°,∠ECB+∠ACB=180°,
∴∠D=∠ACB.
在△ABC与△EAD中,
∴△ABC≌△EAD(AAS),∴AD=BC.
9.80 10.C 11.3 12.(-4,-4)
13.【解析】(1)①(答案不唯一).
(2)证明:∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE.
又∵AD=CE,
∴△BAD≌△ACE(AAS),
∴DB=EA,
∴DE=EA+AD=DB+EC.
14.【解析】(1)证明:∵AD∥BC,
∴∠DAE=∠FCE,∠ADE=∠EFC.
又∵E为AC的中点,∴AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).∴DE=EF.
(2)∵△ADE≌△CFE,∴AD=CF=12.
∵BF∶CF=2∶3,∴BF=8,
∴BC=BF+CF=8+12=20.
素养通关
15.【解析】【特例探究】∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠BAD+∠CAF=90°,
∴∠ABD=∠CAF.
在△ABD和△CAF中,
∴△ABD≌△CAF(AAS).
【归纳证明】∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF,∠AEB=∠CFA.
在△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
【拓展应用】5.
2
