15.2 线段的垂直平分线 课时作业 (含答案)2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 15.2 线段的垂直平分线 课时作业 (含答案)2023-2024学年数学沪科版八年级上册 | 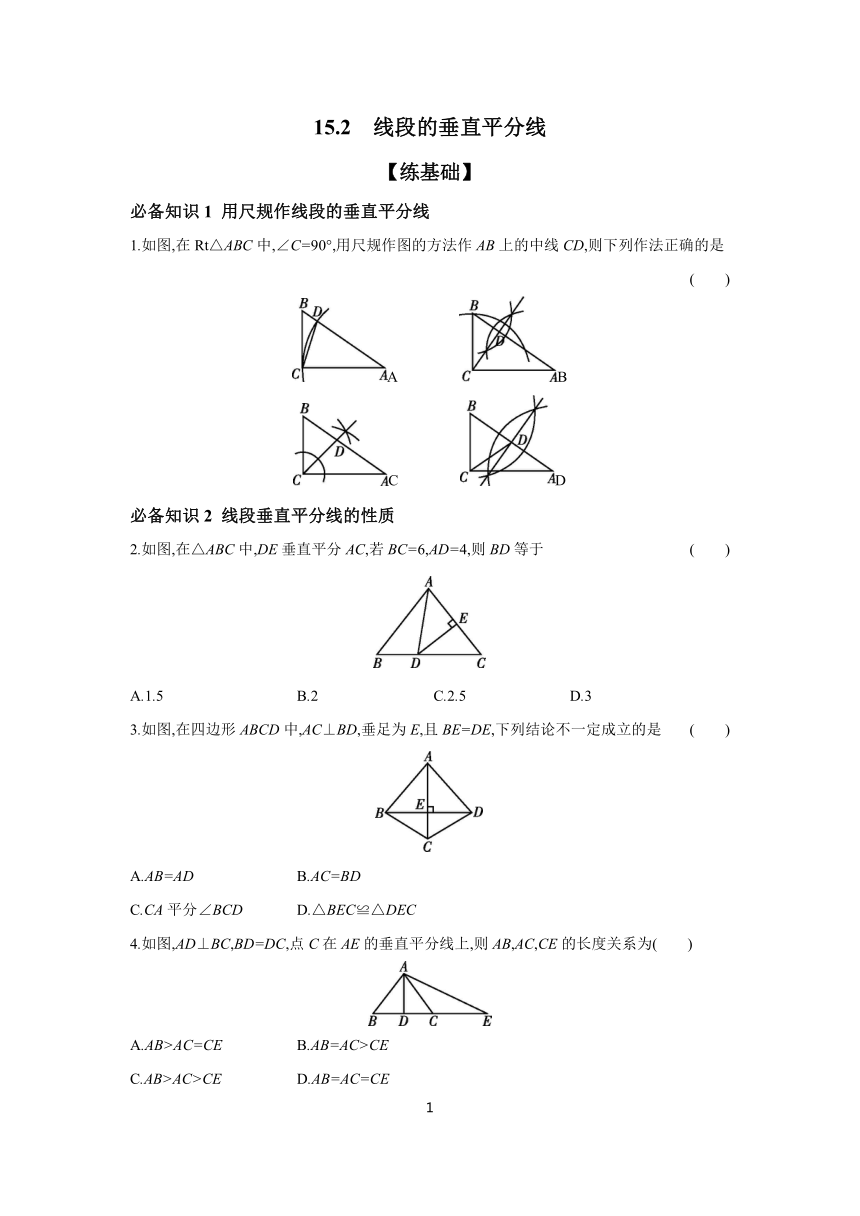 | |
| 格式 | docx | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:32:57 | ||
图片预览


文档简介
15.2 线段的垂直平分线
【练基础】
必备知识1 用尺规作线段的垂直平分线
1.如图,在Rt△ABC中,∠C=90°,用尺规作图的方法作AB上的中线CD,则下列作法正确的是 ( )
A B
C D
必备知识2 线段垂直平分线的性质
2.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于 ( )
A.1.5 B.2 C.2.5 D.3
3.如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,下列结论不一定成立的是 ( )
A.AB=AD B.AC=BD
C.CA平分∠BCD D.△BEC≌△DEC
4.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )
A.AB>AC=CE B.AB=AC>CE
C.AB>AC>CE D.AB=AC=CE
5.如图,在△ABC中,AB=10,边BC的垂直平分线DE分别交AB,BC于点E,D,且AC=6,则△ACE的周长为 ( )
A.16 B.18 C.22 D.26
6.如图,在△ABC中,E是BC上一点,AE=AB,EF垂直平分AC,BD=DE,△ABC的周长为18 cm,AC=7 cm,则DC的长为 ( )
A.4.5 B.5 C.5.5 D.6
7.如图,已知AB比AC长3 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm.求AB和AC的长.
必备知识3 线段垂直平分线的判定
8.下列条件中,不能判定直线MN是线段AB(M,N不在AB上)的垂直平分线的是 ( )
A.MA=MB,NA=NB
B.MA=MB,MN⊥AB
C.MA=NA,MB=NB
D.MA=MB,MN平分AB
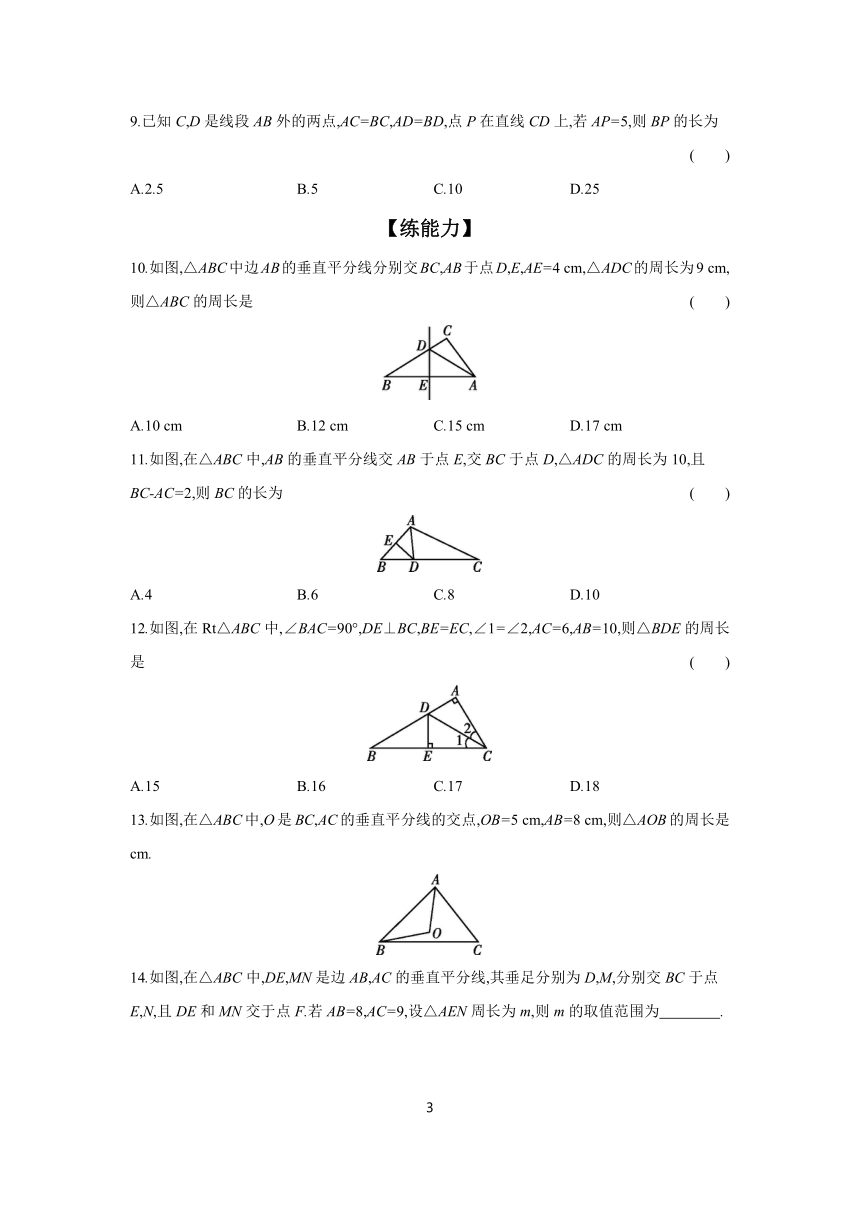
9.已知C,D是线段AB外的两点,AC=BC,AD=BD,点P在直线CD上,若AP=5,则BP的长为 ( )
A.2.5 B.5 C.10 D.25
【练能力】
10.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=4 cm,△ADC的周长为9 cm,则△ABC的周长是 ( )
A.10 cm B.12 cm C.15 cm D.17 cm
11.如图,在△ABC中,AB的垂直平分线交AB于点E,交BC于点D,△ADC的周长为10,且BC-AC=2,则BC的长为 ( )
A.4 B.6 C.8 D.10
12.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,BE=EC,∠1=∠2,AC=6,AB=10,则△BDE的周长是 ( )
A.15 B.16 C.17 D.18
13.如图,在△ABC中,O是BC,AC的垂直平分线的交点,OB=5 cm,AB=8 cm,则△AOB的周长是 cm.
14.如图,在△ABC中,DE,MN是边AB,AC的垂直平分线,其垂足分别为D,M,分别交BC于点E,N,且DE和MN交于点F.若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
15.【马鞍山期末】如图,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20 cm,则AB= .
16.如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
【练素养】
17.如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.
求证:(1)BM=CN.
(2)AM=(AB+AC).
参考答案
基础演练
1.D 2.B 3.B 4.D 5.A 6.C
7.【解析】∵DE垂直平分BC,∴DB=DC.
∵AC+AD+DC=14 cm,
∴AC+AD+BD=14 cm,即AC+AB=14 cm.
设AB=x cm,AC=y cm.根据题意,得
解得
∴AB的长为8.5 cm,AC的长为5.5 cm.
8.C 9.B
能力生成
10.D 11.B 12.B 13.18
14.116.【解析】
证明:如图,连接AE,CE.
∵AC,BD的垂直平分线相交于点E,
∴AE=CE,BE=DE.
在△ABE和△CDE中,
∴△ABE≌△CDE(SSS),
∴∠ABE=∠CDE.
素养通关
17.【解析】证明:(1)如图,连接BD.
∵DE所在直线是BC的垂直平分线,∴BD=CD.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DM⊥AB,DN⊥AC,
∴∠AMD=∠AND=90°.
在△AMD和△AND中,
∴△AMD≌△AND,
∴AM=AN,DM=DN.
又∵∠BMD=∠CND=90°,BD=CD,
∴Rt△BMD≌Rt△CND(HL),∴BM=CN.
(2)∵BM=CN,AM=AN,
∴AB+AC=AM+BM+AN-CN=2AM,
∴AM=(AB+AC).
2
【练基础】
必备知识1 用尺规作线段的垂直平分线
1.如图,在Rt△ABC中,∠C=90°,用尺规作图的方法作AB上的中线CD,则下列作法正确的是 ( )
A B
C D
必备知识2 线段垂直平分线的性质
2.如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于 ( )
A.1.5 B.2 C.2.5 D.3
3.如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,下列结论不一定成立的是 ( )
A.AB=AD B.AC=BD
C.CA平分∠BCD D.△BEC≌△DEC
4.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )
A.AB>AC=CE B.AB=AC>CE
C.AB>AC>CE D.AB=AC=CE
5.如图,在△ABC中,AB=10,边BC的垂直平分线DE分别交AB,BC于点E,D,且AC=6,则△ACE的周长为 ( )
A.16 B.18 C.22 D.26
6.如图,在△ABC中,E是BC上一点,AE=AB,EF垂直平分AC,BD=DE,△ABC的周长为18 cm,AC=7 cm,则DC的长为 ( )
A.4.5 B.5 C.5.5 D.6
7.如图,已知AB比AC长3 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm.求AB和AC的长.
必备知识3 线段垂直平分线的判定
8.下列条件中,不能判定直线MN是线段AB(M,N不在AB上)的垂直平分线的是 ( )
A.MA=MB,NA=NB
B.MA=MB,MN⊥AB
C.MA=NA,MB=NB
D.MA=MB,MN平分AB
9.已知C,D是线段AB外的两点,AC=BC,AD=BD,点P在直线CD上,若AP=5,则BP的长为 ( )
A.2.5 B.5 C.10 D.25
【练能力】
10.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=4 cm,△ADC的周长为9 cm,则△ABC的周长是 ( )
A.10 cm B.12 cm C.15 cm D.17 cm
11.如图,在△ABC中,AB的垂直平分线交AB于点E,交BC于点D,△ADC的周长为10,且BC-AC=2,则BC的长为 ( )
A.4 B.6 C.8 D.10
12.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,BE=EC,∠1=∠2,AC=6,AB=10,则△BDE的周长是 ( )
A.15 B.16 C.17 D.18
13.如图,在△ABC中,O是BC,AC的垂直平分线的交点,OB=5 cm,AB=8 cm,则△AOB的周长是 cm.
14.如图,在△ABC中,DE,MN是边AB,AC的垂直平分线,其垂足分别为D,M,分别交BC于点E,N,且DE和MN交于点F.若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
15.【马鞍山期末】如图,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20 cm,则AB= .
16.如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
【练素养】
17.如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.
求证:(1)BM=CN.
(2)AM=(AB+AC).
参考答案
基础演练
1.D 2.B 3.B 4.D 5.A 6.C
7.【解析】∵DE垂直平分BC,∴DB=DC.
∵AC+AD+DC=14 cm,
∴AC+AD+BD=14 cm,即AC+AB=14 cm.
设AB=x cm,AC=y cm.根据题意,得
解得
∴AB的长为8.5 cm,AC的长为5.5 cm.
8.C 9.B
能力生成
10.D 11.B 12.B 13.18
14.1
证明:如图,连接AE,CE.
∵AC,BD的垂直平分线相交于点E,
∴AE=CE,BE=DE.
在△ABE和△CDE中,
∴△ABE≌△CDE(SSS),
∴∠ABE=∠CDE.
素养通关
17.【解析】证明:(1)如图,连接BD.
∵DE所在直线是BC的垂直平分线,∴BD=CD.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DM⊥AB,DN⊥AC,
∴∠AMD=∠AND=90°.
在△AMD和△AND中,
∴△AMD≌△AND,
∴AM=AN,DM=DN.
又∵∠BMD=∠CND=90°,BD=CD,
∴Rt△BMD≌Rt△CND(HL),∴BM=CN.
(2)∵BM=CN,AM=AN,
∴AB+AC=AM+BM+AN-CN=2AM,
∴AM=(AB+AC).
2
