15.3 课时1 等腰三角形的性质 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 15.3 课时1 等腰三角形的性质 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 11:36:45 | ||
图片预览


文档简介
15.3 课时1 等腰三角形的性质
【练基础】
必备知识1 等边对等角
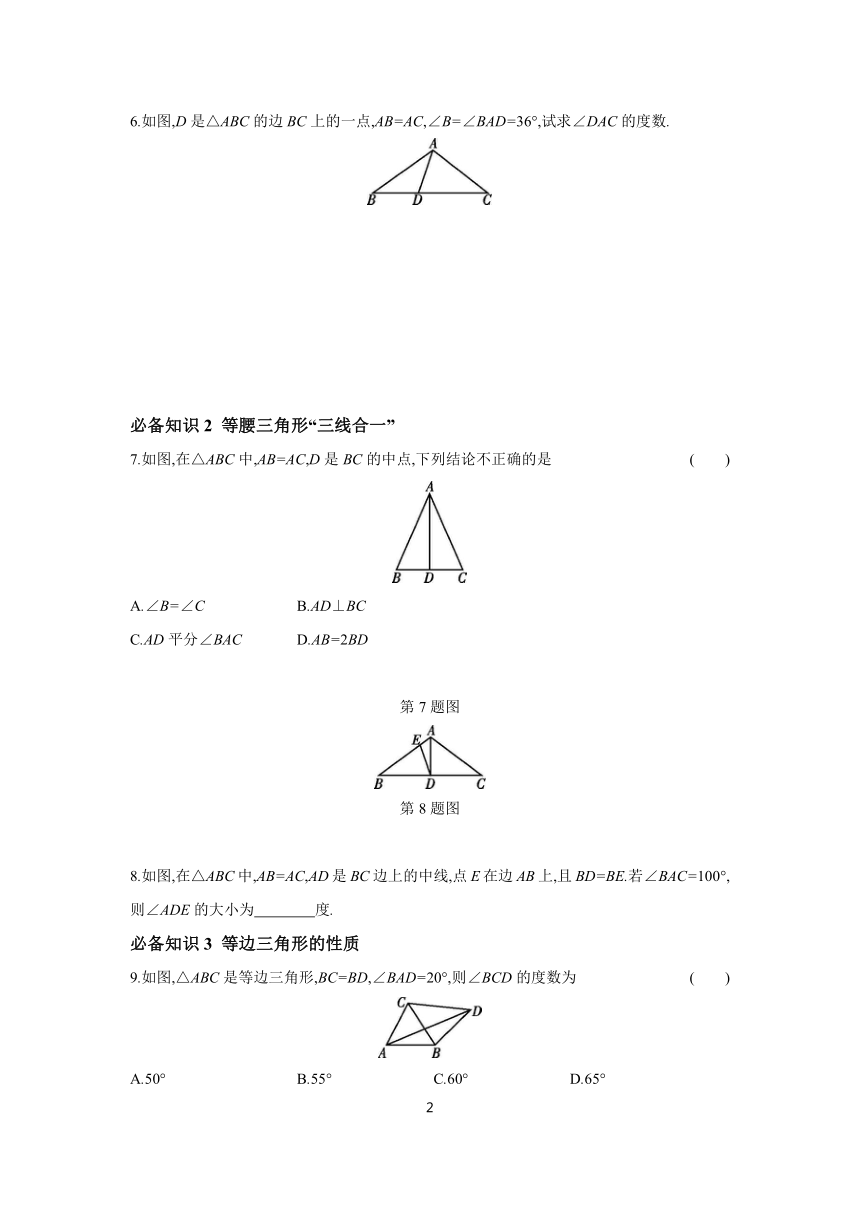
1.如图,在△ABC中,∠A=45°,∠B=60°,点D在边AB上,且BD=BC,连接CD,则∠ACD的大小为 ( )
A.30°
B.25°
C.15°
D.10°
2.如图,AB=AC,CD=CE.过点C的直线FG与DE平行,若∠A=38°,则∠1的度数为 ( )
A.42° B.54.5°
C.58° D.62.5°
3.如图,在△ABC中,AB=AD=DC,∠B=64°,则∠C的度数为 ( )
A.30° B.32°
C.40° D.48°
4.在等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C= °.
5.如图,已知在△ABC中,AB=AC,BD⊥AC于点D,∠A=50°,则∠DBC的度数是 .
6.如图,D是△ABC的边BC上的一点,AB=AC,∠B=∠BAD=36°,试求∠DAC的度数.
必备知识2 等腰三角形“三线合一”
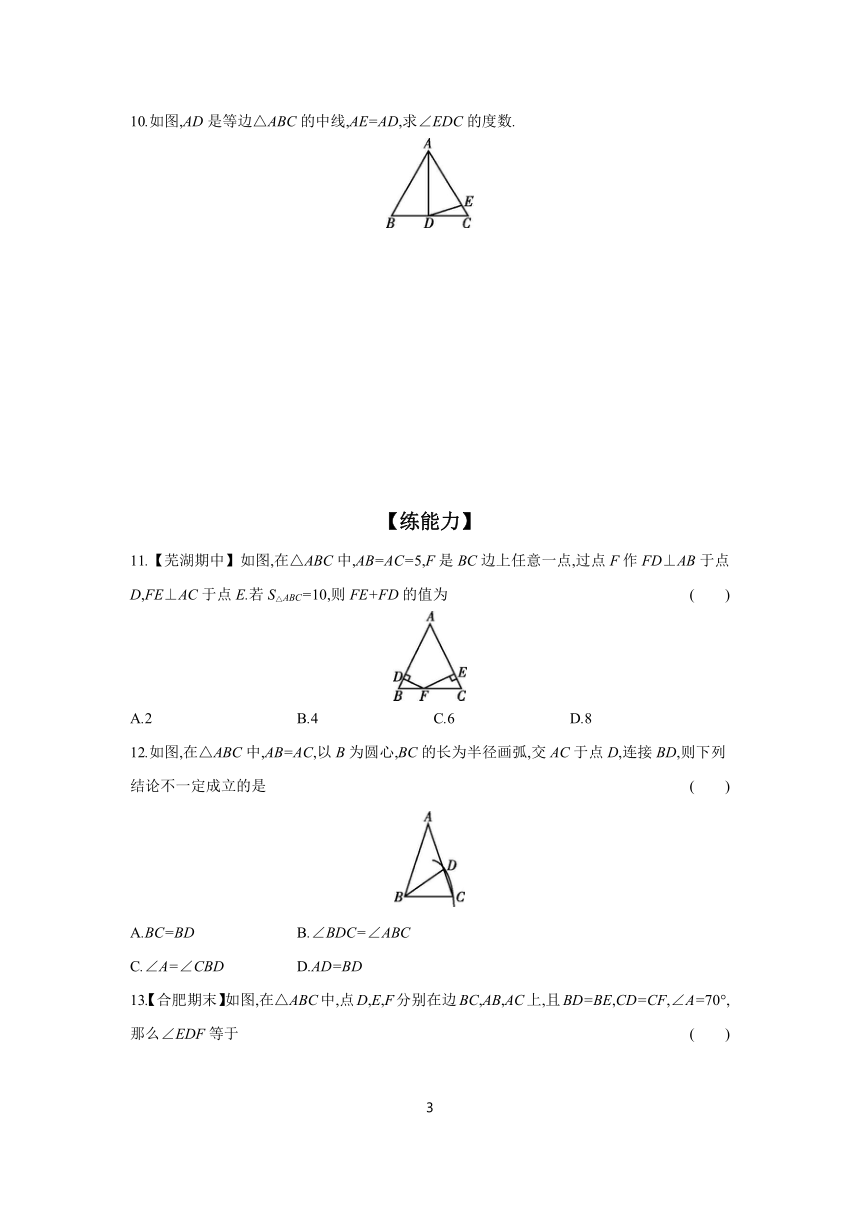
7.如图,在△ABC中,AB=AC,D是BC的中点,下列结论不正确的是 ( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
第7题图
第8题图
8.如图,在△ABC中,AB=AC,AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为 度.
必备知识3 等边三角形的性质
9.如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为 ( )
A.50° B.55° C.60° D.65°
10.如图,AD是等边△ABC的中线,AE=AD,求∠EDC的度数.
【练能力】
11.【芜湖期中】如图,在△ABC中,AB=AC=5,F是BC边上任意一点,过点F作FD⊥AB于点D,FE⊥AC于点E.若S△ABC=10,则FE+FD的值为 ( )
A.2 B.4 C.6 D.8
12.如图,在△ABC中,AB=AC,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则下列结论不一定成立的是 ( )
A.BC=BD B.∠BDC=∠ABC
C.∠A=∠CBD D.AD=BD
13.【合肥期末】如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,且BD=BE,CD=CF,∠A=70°,那么∠EDF等于 ( )
A.40° B.45° C.50° D.55°
14.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为 ( )
A.3 B.4 C.5 D.6
15.如图,AB=AC,∠C=36°,AC的垂直平分线MN交BC于点D,则∠DAB= .
16.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求证:CE=CF.
(2)若CD=2,求DF的长.
17.如图,AD为等腰△ABC的顶角∠BAC的平分线,∠ABC=50°,在线段AD上取一点E,连接CE,使得∠ACE=20°,在线段CE上取一点F,连接BF,使得∠FBC=10°,连接BE,AF.
(1)∠EBF= °,∠EBA= °,∠BFE= °.
(2)求证:BA=BF.
(3)BE与AF的位置关系为 .(直接写出)
18.在△ABC中,AB=AC.
(1)①如图1,若∠BAD=30°,AD是BC边上的高,AD=AE,则∠EDC= ;
②如图2,若∠BAD=40°,AD是BC边上的高,AD=AE,则∠EDC= .
(2)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系 请用式子表示.
(3)如图3,如果AD不是BC边上的高,AD=AE,是否仍有上述关系 请说明理由.
【练素养】
19.已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:AD=BE.
(2)求∠AEB的度数.
(3)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①∠AEB的度数为 °;
②探索线段CM,AE,BE之间的数量关系为 .(直接写出答案,不需要说明理由)
参考答案
基础演练
1.C 2.B 3.B 4.80 5.25°
6.【解析】∵AB=AC,∠B=∠BAD=36°,
∴∠C=∠B=36°,∠ADC=∠B+∠BAD=36°+36°=72°,
∴∠DAC=180°-∠C-∠ADC=180°-36°-72°=72°.
7.D 8.20 9.A
10.【解析】∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,∴∠ADC=90°.
∵AD=AE,
∴∠ADE=∠AED==75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
能力生成
11.B 12.D 13.D 14.B 15.72°
16.【解析】(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE∥AB,
∴∠B=∠EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°.
∵EF⊥ED,
∴∠DEF=90°,∴∠F=30°.
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,∴CE=CF.
(2)由(1)可知∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2.
又∵CE=CF,∴CF=2,
∴DF=DC+CF=2+2=4.
17.【解析】(1)20;20;40.
(2)证明:∵AD为等腰△ABC的顶角∠BAC的平分线,
∴∠BAE=∠BAC.
∵∠ABC=∠ACB=50°,
∴∠BAC=80°,
∴∠BAE=40°,
∴∠BAE=∠BFE=40°.
∵∠ABE=∠EBF=20°,BE=BE,
∴△ABE≌△FBE(AAS),
∴AB=BF.
(3)BE⊥AF.
18.【解析】(1)①15°;②20°.
(2)∠BAD=2∠EDC(或∠EDC=∠BAD).
(3)仍成立.
理由:∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C.
又∵AB=AC,∴∠B=∠C,
∴∠BAD=2∠EDC.
素养通关
19.【解析】(1)证明:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=60°.
(3)①90;②AE=BE+2CM.
提示:①∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴BE=AD,∠BEC=∠ADC.
∵点A,D,E在同一直线上,
∴∠ADC=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°.
②如题图2,∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM.
∵△ACD≌△BCE(已证),
∴BE=AD,
∴AE=AD+DE=BE+2CM.
2
【练基础】
必备知识1 等边对等角
1.如图,在△ABC中,∠A=45°,∠B=60°,点D在边AB上,且BD=BC,连接CD,则∠ACD的大小为 ( )
A.30°
B.25°
C.15°
D.10°
2.如图,AB=AC,CD=CE.过点C的直线FG与DE平行,若∠A=38°,则∠1的度数为 ( )
A.42° B.54.5°
C.58° D.62.5°
3.如图,在△ABC中,AB=AD=DC,∠B=64°,则∠C的度数为 ( )
A.30° B.32°
C.40° D.48°
4.在等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C= °.
5.如图,已知在△ABC中,AB=AC,BD⊥AC于点D,∠A=50°,则∠DBC的度数是 .
6.如图,D是△ABC的边BC上的一点,AB=AC,∠B=∠BAD=36°,试求∠DAC的度数.
必备知识2 等腰三角形“三线合一”
7.如图,在△ABC中,AB=AC,D是BC的中点,下列结论不正确的是 ( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
第7题图
第8题图
8.如图,在△ABC中,AB=AC,AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为 度.
必备知识3 等边三角形的性质
9.如图,△ABC是等边三角形,BC=BD,∠BAD=20°,则∠BCD的度数为 ( )
A.50° B.55° C.60° D.65°
10.如图,AD是等边△ABC的中线,AE=AD,求∠EDC的度数.
【练能力】
11.【芜湖期中】如图,在△ABC中,AB=AC=5,F是BC边上任意一点,过点F作FD⊥AB于点D,FE⊥AC于点E.若S△ABC=10,则FE+FD的值为 ( )
A.2 B.4 C.6 D.8
12.如图,在△ABC中,AB=AC,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则下列结论不一定成立的是 ( )
A.BC=BD B.∠BDC=∠ABC
C.∠A=∠CBD D.AD=BD
13.【合肥期末】如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,且BD=BE,CD=CF,∠A=70°,那么∠EDF等于 ( )
A.40° B.45° C.50° D.55°
14.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为 ( )
A.3 B.4 C.5 D.6
15.如图,AB=AC,∠C=36°,AC的垂直平分线MN交BC于点D,则∠DAB= .
16.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求证:CE=CF.
(2)若CD=2,求DF的长.
17.如图,AD为等腰△ABC的顶角∠BAC的平分线,∠ABC=50°,在线段AD上取一点E,连接CE,使得∠ACE=20°,在线段CE上取一点F,连接BF,使得∠FBC=10°,连接BE,AF.
(1)∠EBF= °,∠EBA= °,∠BFE= °.
(2)求证:BA=BF.
(3)BE与AF的位置关系为 .(直接写出)
18.在△ABC中,AB=AC.
(1)①如图1,若∠BAD=30°,AD是BC边上的高,AD=AE,则∠EDC= ;
②如图2,若∠BAD=40°,AD是BC边上的高,AD=AE,则∠EDC= .
(2)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系 请用式子表示.
(3)如图3,如果AD不是BC边上的高,AD=AE,是否仍有上述关系 请说明理由.
【练素养】
19.已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:AD=BE.
(2)求∠AEB的度数.
(3)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①∠AEB的度数为 °;
②探索线段CM,AE,BE之间的数量关系为 .(直接写出答案,不需要说明理由)
参考答案
基础演练
1.C 2.B 3.B 4.80 5.25°
6.【解析】∵AB=AC,∠B=∠BAD=36°,
∴∠C=∠B=36°,∠ADC=∠B+∠BAD=36°+36°=72°,
∴∠DAC=180°-∠C-∠ADC=180°-36°-72°=72°.
7.D 8.20 9.A
10.【解析】∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,∴∠ADC=90°.
∵AD=AE,
∴∠ADE=∠AED==75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
能力生成
11.B 12.D 13.D 14.B 15.72°
16.【解析】(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE∥AB,
∴∠B=∠EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°.
∵EF⊥ED,
∴∠DEF=90°,∴∠F=30°.
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,∴CE=CF.
(2)由(1)可知∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2.
又∵CE=CF,∴CF=2,
∴DF=DC+CF=2+2=4.
17.【解析】(1)20;20;40.
(2)证明:∵AD为等腰△ABC的顶角∠BAC的平分线,
∴∠BAE=∠BAC.
∵∠ABC=∠ACB=50°,
∴∠BAC=80°,
∴∠BAE=40°,
∴∠BAE=∠BFE=40°.
∵∠ABE=∠EBF=20°,BE=BE,
∴△ABE≌△FBE(AAS),
∴AB=BF.
(3)BE⊥AF.
18.【解析】(1)①15°;②20°.
(2)∠BAD=2∠EDC(或∠EDC=∠BAD).
(3)仍成立.
理由:∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C.
又∵AB=AC,∴∠B=∠C,
∴∠BAD=2∠EDC.
素养通关
19.【解析】(1)证明:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=60°.
(3)①90;②AE=BE+2CM.
提示:①∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴BE=AD,∠BEC=∠ADC.
∵点A,D,E在同一直线上,
∴∠ADC=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°.
②如题图2,∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM.
∵△ACD≌△BCE(已证),
∴BE=AD,
∴AE=AD+DE=BE+2CM.
2
