15.3 课时2 等腰三角形的判定 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 15.3 课时2 等腰三角形的判定 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 164.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:34:35 | ||
图片预览


文档简介
15.3 课时2 等腰三角形的判定
【练基础】
必备知识1 等角对等边
1.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是 ( )
A.30°、60° B.40°、70°
C.50°、60° D.100°、30°
2.在证明等腰三角形的判定定理“等角对等边”,即“如图,已知:∠B=∠C,求证:AB=AC”时,小明作了如下的辅助线,下列对辅助线的描述正确的有 ( )
①作∠BAC的平分线AD交BC于点D
②取BC边的中点D,连接AD
③过点A作AD⊥BC,垂足为D
④作BC边的垂直平分线AD,交BC于点D
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 ( )
A.0 B.1
C.2 D.3
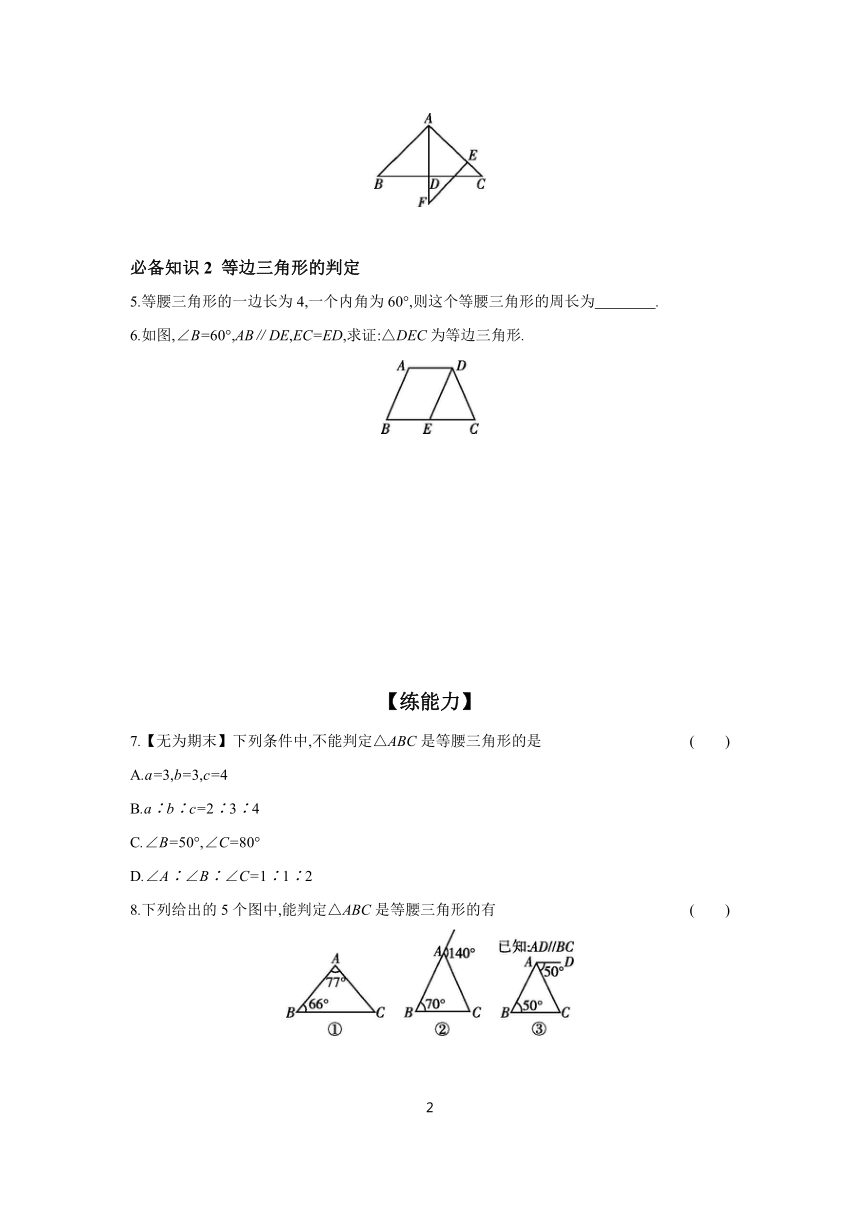
4.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠B=39°,求∠CAD的度数.
(2)若点E在边AC上,EF∥AB交AD的延长线于点F.求证:AE=FE.
必备知识2 等边三角形的判定
5.等腰三角形的一边长为4,一个内角为60°,则这个等腰三角形的周长为 .
6.如图,∠B=60°,AB∥DE,EC=ED,求证:△DEC为等边三角形.
【练能力】
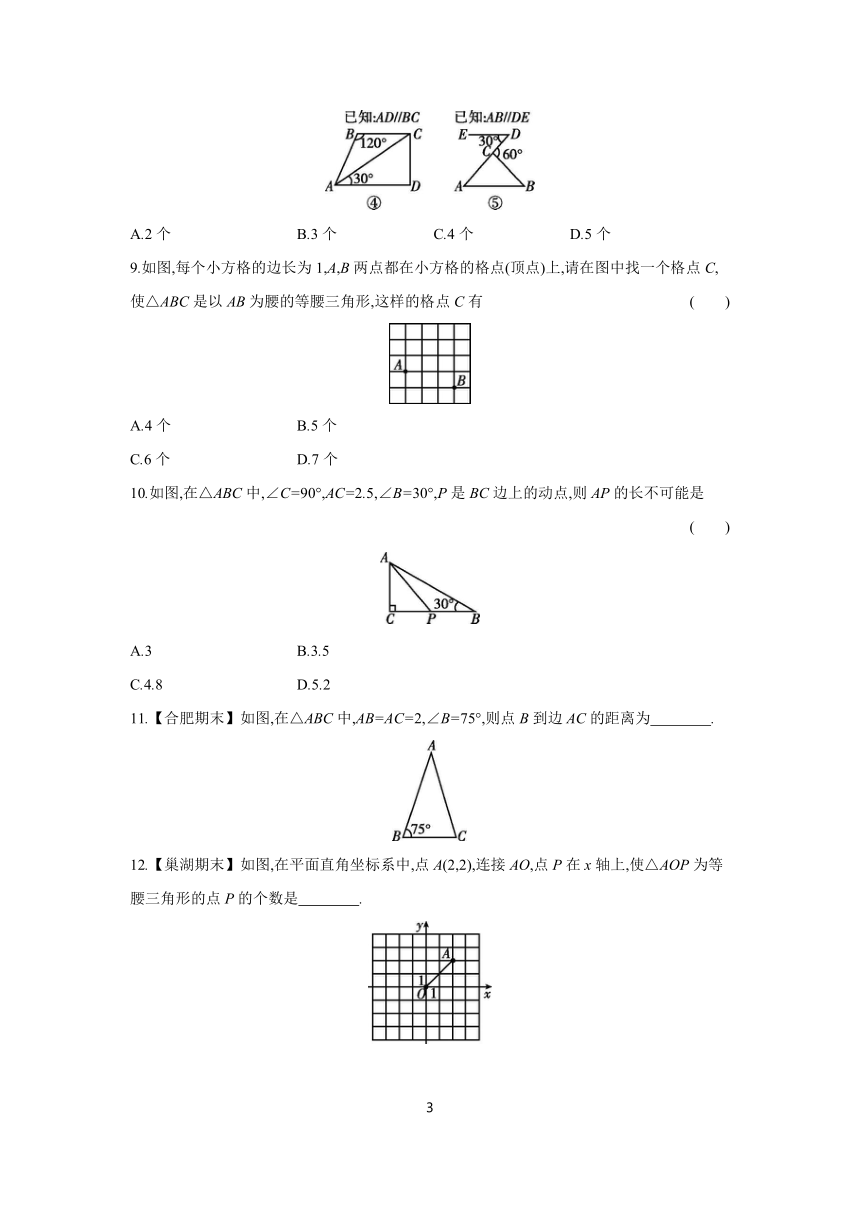
7.【无为期末】下列条件中,不能判定△ABC是等腰三角形的是 ( )
A.a=3,b=3,c=4
B.a∶b∶c=2∶3∶4
C.∠B=50°,∠C=80°
D.∠A∶∠B∶∠C=1∶1∶2
8.下列给出的5个图中,能判定△ABC是等腰三角形的有 ( )
A.2个 B.3个 C.4个 D.5个
9.如图,每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有 ( )
A.4个 B.5个
C.6个 D.7个
10.如图,在△ABC中,∠C=90°,AC=2.5,∠B=30°,P是BC边上的动点,则AP的长不可能是 ( )
A.3 B.3.5
C.4.8 D.5.2
11.【合肥期末】如图,在△ABC中,AB=AC=2,∠B=75°,则点B到边AC的距离为 .
12.【巢湖期末】如图,在平面直角坐标系中,点A(2,2),连接AO,点P在x轴上,使△AOP为等腰三角形的点P的个数是 .
13.如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找一点P,使△ABP是等腰三角形,则∠APB的度数为 .
14.如图,在∠MON的边ON上顺次取点P1,P3,P5,…,在边OM上顺次取点P2,P4,P6,…,使得OP1=P1P2=P2P3=P3P4=P4P5=…,得到等腰△OP1P2,△P1P2P3,△P2P3P4,△P3P4P5,….
(1)若∠MON=30°,可以得到的最后一个等腰三角形是 .
(2)若按照上述方式操作,得到的最后一个等腰三角形是△P3P4P5,则∠MON的度数α的取值范围是 .
15.如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于点E.求证:△ADE是等边三角形.
16.在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.
(1)如图1,若AD=BD,求∠A的度数.
(2)如图2,在(1)的条件下,作DE⊥AB于点E,连接EC.求证:△EBC是等边三角形.
【练素养】
17.如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.
(1)△AMN是否是等腰三角形 说明理由.
(2)P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.
①求证:△BPM是等腰三角形;
②若△ABC的周长为a,BC=b(a>2b),求△AMN的周长(用含a,b的式子表示).
参考答案
基础演练
1.B 2.B 3.D
4.【解析】(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,又∠B=39°,
∴∠BAD=∠CAD=90°-39°=51°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AB,
∴∠F=∠BAD,
∴∠F=∠CAD,
∴AE=FE.
5.12
6.【解析】证明:∵AB∥DE,
∴∠DEC=∠B=60°.
∵EC=ED,
∴△DEC为等边三角形.
能力生成
7.B 8.C 9.C 10.D 11.1 12.4
13.20°或40°或70°或100°
14.(1)△P1P2P3 (2)18°≤α<22.5°
15.【解析】证明:∵△ABC为等边三角形,EC平分∠ACB外角,
∴∠B=∠ACB=∠ACE=60°.
如图,过点D作AC的平行线交AB于点P,
∴∠BDP=∠ACB=60°,
∴△BDP为等边三角形,BD=BP,∠APD=∠DCE=120°,
∴AP=CD.
∵∠BPD为△ADP的外角,
∴∠ADP+∠DAP=∠BPD=60°.
∵∠ADP+∠EDC=180°-∠BDP-∠ADE=60°,
∴∠DAP=∠EDC.
在△ADP和△DEC中,
∴△ADP≌△DEC(ASA),∴AD=DE.
∵∠ADE=60°,∴△ADE是等边三角形.
16.【解析】(1)∵AD=BD,∴∠A=∠DBA.
∵BD是△ABC的角平分线,∴∠DBA=∠DBC,
∴∠A=∠DBA=∠DBC.
∵∠ACB=90°,∴∠A+∠DBA+∠DBC=90°,
∴∠A=30°.
(2)证明:∵AD=BD,DE⊥AB,∴AE=BE,
∴CE=BE.
∵∠A=30°,∴∠EBC=60°,
∴△EBC是等边三角形.
素养通关
17.【解析】(1)△AMN是等腰三角形.
理由如下:∵AB=AC,∴∠ABC=∠ACB.
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴△AMN是等腰三角形.
(2)①证明:∵BP平分∠ABC,
∴∠PBM=∠PBC.
∵MN∥BC,
∴∠MPB=∠PBC,
∴∠PBM=∠MPB,
∴MB=MP,
∴△BPM是等腰三角形.
②由①知MB=MP,同理可得NC=NP,
∴△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC.
∵△ABC的周长为a,BC=b,
∴AB+AC+b=a,
∴AB+AC=a-b,
∴△AMN的周长=a-b.
2
【练基础】
必备知识1 等角对等边
1.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是 ( )
A.30°、60° B.40°、70°
C.50°、60° D.100°、30°
2.在证明等腰三角形的判定定理“等角对等边”,即“如图,已知:∠B=∠C,求证:AB=AC”时,小明作了如下的辅助线,下列对辅助线的描述正确的有 ( )
①作∠BAC的平分线AD交BC于点D
②取BC边的中点D,连接AD
③过点A作AD⊥BC,垂足为D
④作BC边的垂直平分线AD,交BC于点D
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 ( )
A.0 B.1
C.2 D.3
4.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠B=39°,求∠CAD的度数.
(2)若点E在边AC上,EF∥AB交AD的延长线于点F.求证:AE=FE.
必备知识2 等边三角形的判定
5.等腰三角形的一边长为4,一个内角为60°,则这个等腰三角形的周长为 .
6.如图,∠B=60°,AB∥DE,EC=ED,求证:△DEC为等边三角形.
【练能力】
7.【无为期末】下列条件中,不能判定△ABC是等腰三角形的是 ( )
A.a=3,b=3,c=4
B.a∶b∶c=2∶3∶4
C.∠B=50°,∠C=80°
D.∠A∶∠B∶∠C=1∶1∶2
8.下列给出的5个图中,能判定△ABC是等腰三角形的有 ( )
A.2个 B.3个 C.4个 D.5个
9.如图,每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有 ( )
A.4个 B.5个
C.6个 D.7个
10.如图,在△ABC中,∠C=90°,AC=2.5,∠B=30°,P是BC边上的动点,则AP的长不可能是 ( )
A.3 B.3.5
C.4.8 D.5.2
11.【合肥期末】如图,在△ABC中,AB=AC=2,∠B=75°,则点B到边AC的距离为 .
12.【巢湖期末】如图,在平面直角坐标系中,点A(2,2),连接AO,点P在x轴上,使△AOP为等腰三角形的点P的个数是 .
13.如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找一点P,使△ABP是等腰三角形,则∠APB的度数为 .
14.如图,在∠MON的边ON上顺次取点P1,P3,P5,…,在边OM上顺次取点P2,P4,P6,…,使得OP1=P1P2=P2P3=P3P4=P4P5=…,得到等腰△OP1P2,△P1P2P3,△P2P3P4,△P3P4P5,….
(1)若∠MON=30°,可以得到的最后一个等腰三角形是 .
(2)若按照上述方式操作,得到的最后一个等腰三角形是△P3P4P5,则∠MON的度数α的取值范围是 .
15.如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于点E.求证:△ADE是等边三角形.
16.在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.
(1)如图1,若AD=BD,求∠A的度数.
(2)如图2,在(1)的条件下,作DE⊥AB于点E,连接EC.求证:△EBC是等边三角形.
【练素养】
17.如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.
(1)△AMN是否是等腰三角形 说明理由.
(2)P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.
①求证:△BPM是等腰三角形;
②若△ABC的周长为a,BC=b(a>2b),求△AMN的周长(用含a,b的式子表示).
参考答案
基础演练
1.B 2.B 3.D
4.【解析】(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,又∠B=39°,
∴∠BAD=∠CAD=90°-39°=51°.
(2)证明:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD.
∵EF∥AB,
∴∠F=∠BAD,
∴∠F=∠CAD,
∴AE=FE.
5.12
6.【解析】证明:∵AB∥DE,
∴∠DEC=∠B=60°.
∵EC=ED,
∴△DEC为等边三角形.
能力生成
7.B 8.C 9.C 10.D 11.1 12.4
13.20°或40°或70°或100°
14.(1)△P1P2P3 (2)18°≤α<22.5°
15.【解析】证明:∵△ABC为等边三角形,EC平分∠ACB外角,
∴∠B=∠ACB=∠ACE=60°.
如图,过点D作AC的平行线交AB于点P,
∴∠BDP=∠ACB=60°,
∴△BDP为等边三角形,BD=BP,∠APD=∠DCE=120°,
∴AP=CD.
∵∠BPD为△ADP的外角,
∴∠ADP+∠DAP=∠BPD=60°.
∵∠ADP+∠EDC=180°-∠BDP-∠ADE=60°,
∴∠DAP=∠EDC.
在△ADP和△DEC中,
∴△ADP≌△DEC(ASA),∴AD=DE.
∵∠ADE=60°,∴△ADE是等边三角形.
16.【解析】(1)∵AD=BD,∴∠A=∠DBA.
∵BD是△ABC的角平分线,∴∠DBA=∠DBC,
∴∠A=∠DBA=∠DBC.
∵∠ACB=90°,∴∠A+∠DBA+∠DBC=90°,
∴∠A=30°.
(2)证明:∵AD=BD,DE⊥AB,∴AE=BE,
∴CE=BE.
∵∠A=30°,∴∠EBC=60°,
∴△EBC是等边三角形.
素养通关
17.【解析】(1)△AMN是等腰三角形.
理由如下:∵AB=AC,∴∠ABC=∠ACB.
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴△AMN是等腰三角形.
(2)①证明:∵BP平分∠ABC,
∴∠PBM=∠PBC.
∵MN∥BC,
∴∠MPB=∠PBC,
∴∠PBM=∠MPB,
∴MB=MP,
∴△BPM是等腰三角形.
②由①知MB=MP,同理可得NC=NP,
∴△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC.
∵△ABC的周长为a,BC=b,
∴AB+AC+b=a,
∴AB+AC=a-b,
∴△AMN的周长=a-b.
2
