15.4 课时2 角的平分线的判定 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 15.4 课时2 角的平分线的判定 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 186.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:37:02 | ||
图片预览



文档简介
15.4 课时2 角的平分线的判定
【练基础】
必备知识 角的平分线的判定
1.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是 ( )
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
2.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=26°,则∠A的度数为 ( )
A.40° B.34° C.36° D.38°
3.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于 ( )
A.110° B.115° C.125° D.130°
4.如图,∠CDA=∠CBA=90°,且CD=CB,则点C在∠ 的平分线上,点A在∠ 的平分线上.
5.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.求证:AD平分∠BAC.
6.如图,D,E,F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等.求证:AD平分∠BAC.
【练能力】
7.到三角形三边的距离相等的是 ( )
A.三条中线交点
B.三条角平分线的交点
C.三条高的交点
D.三条中垂线的交点
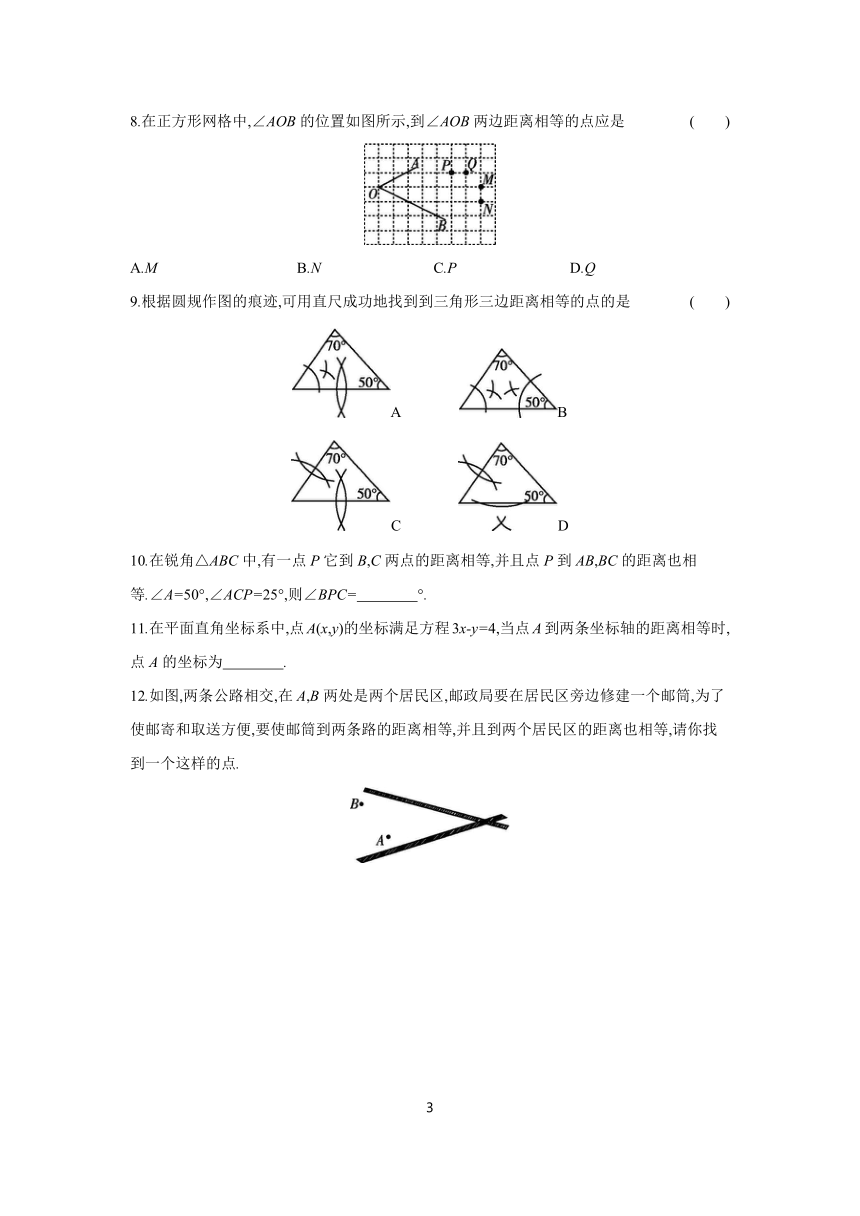
8.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是 ( )
A.M B.N C.P D.Q
9.根据圆规作图的痕迹,可用直尺成功地找到到三角形三边距离相等的点的是 ( )
A B
C D
10.在锐角△ABC中,有一点P它到B,C两点的距离相等,并且点P到AB,BC的距离也相等.∠A=50°,∠ACP=25°,则∠BPC= °.
11.在平面直角坐标系中,点A(x,y)的坐标满足方程3x-y=4,当点A到两条坐标轴的距离相等时,点A的坐标为 .
12.如图,两条公路相交,在A,B两处是两个居民区,邮政局要在居民区旁边修建一个邮筒,为了使邮寄和取送方便,要使邮筒到两条路的距离相等,并且到两个居民区的距离也相等,请你找到一个这样的点.
13.如图,∠ABC=60°,点D在AC上,ED=6,DE⊥BC,DF⊥AB,且DE=DF.
求:(1)∠ABD的度数.
(2)DB的长度.
14.如图,在△ABC中,BE⊥AC于点E,BC的垂直平分线分别交AB,BE于点D,G,垂足为H,CD⊥AB,CD交BE于点F.
(1)求证:△BDF≌△CDA,并写出BF与AC的数量关系.
(2)若DF=DG,求证:①BE平分∠ABC.②CE=BF.
【练素养】
15.如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F,交AC于点E,过点O作OD⊥BC于点D.
(1)求证:∠AOB=90°+∠C.
(2)求证:AE+BF=EF.
(3)若OD=a,CE+CF=2b,请用含a,b的代数式表示△CEF的面积,S△CEF= (直接写出结果).
参考答案
基础演练
1.A 2.D 3.A
4.BAD BCD
5.【解析】证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,∴AD平分∠BAC.
6.【解析】
证明:如图,过点D作DM⊥AB于点M,DN⊥AC于点N.∵△DCE的面积与△DBF的面积相等,
∴=.
∵CE=BF,∴DM=DN,
∴AD平分∠BAC.
能力生成
7.B 8.A 9.B 10.110 11.(2,2)或(1,-1)
12.【解析】点P到A,B两点的距离相等,根据性质:线段垂直平分线上的点到线段两个端点的距离相等.需用尺规作出线段AB的垂直平分线;点P到两相交直线CD,EF的距离相等,根据性质:角平分线上的点到角两边的距离相等.需用尺规作出∠COF的平分线,P为∠COF的平分线与线段AB的垂直平分线的交点.如图所示.
13.【解析】(1)∵DE⊥BC,DF⊥AB,
且DE=DF,
∴DB平分∠ABC,
即∠ABD=∠ABC=×60°=30°.
(2)在直角三角形BED中,
∵∠DBE=∠ABC=×60°=30°,
又∵DE=6,
∴BD=2DE=12.
14.【解析】证明:(1)∵DH垂直平分BC,
∴BD=CD.
∵BE⊥AC,BA⊥CD,
∴∠ADC=∠BDF=90°.
∵∠A+∠DBF=90°,∠DBF+∠DFB=90°,
∴∠A=∠DFB.
在△ADC和△FDB中,
∴△ADC≌△FDB(AAS),
∴BF=AC.
(2)①∵DF=DG,
∴∠DGF=∠DFG.
∵∠BGH=∠DGF,
∴∠BGH=∠DFG.
∵∠DBF+∠DFB=90°,∠FBC+∠BGH=90°,
∴∠DBF=∠FBC,
∴BE平分∠ABC.
②在△ABE和△CBE中,
∴△ABE≌△CBE(ASA),
∴AE=CE,
∴AC=2CE.
∵BF=AC,
∴CE=BF.
素养通关
15.【解析】(1)证明:∵OA,OB分别平分∠BAC和∠ABC,
∴∠OAB=∠OAE=∠BAC,∠OBA=∠OBF=∠ABC,
∴∠AOB=180°-∠OAB-∠OBA=180°-∠CAB-∠ABC=180°-(∠CAB+∠ABC)=180°-(180°-∠C)=90°+∠C.
(2)证明:∵EF∥AB,
∴∠OAB=∠AOE,∠ABO=∠BOF.
又∠OAB=∠EAO,∠OBA=∠OBF,
∴∠AOE=∠EAO,∠BOF=∠OBF,
∴AE=OE,BF=OF,
∴EF=OE+OF=AE+BF.
(3)ab.
提示:∵点O在∠ACB的平分线上,
∴点O到AC的距离等于OD,
∴S△CEF=(CE+CF)·OD=×2b·a=ab.
2
【练基础】
必备知识 角的平分线的判定
1.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是 ( )
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
2.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=26°,则∠A的度数为 ( )
A.40° B.34° C.36° D.38°
3.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于 ( )
A.110° B.115° C.125° D.130°
4.如图,∠CDA=∠CBA=90°,且CD=CB,则点C在∠ 的平分线上,点A在∠ 的平分线上.
5.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.求证:AD平分∠BAC.
6.如图,D,E,F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等.求证:AD平分∠BAC.
【练能力】
7.到三角形三边的距离相等的是 ( )
A.三条中线交点
B.三条角平分线的交点
C.三条高的交点
D.三条中垂线的交点
8.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是 ( )
A.M B.N C.P D.Q
9.根据圆规作图的痕迹,可用直尺成功地找到到三角形三边距离相等的点的是 ( )
A B
C D
10.在锐角△ABC中,有一点P它到B,C两点的距离相等,并且点P到AB,BC的距离也相等.∠A=50°,∠ACP=25°,则∠BPC= °.
11.在平面直角坐标系中,点A(x,y)的坐标满足方程3x-y=4,当点A到两条坐标轴的距离相等时,点A的坐标为 .
12.如图,两条公路相交,在A,B两处是两个居民区,邮政局要在居民区旁边修建一个邮筒,为了使邮寄和取送方便,要使邮筒到两条路的距离相等,并且到两个居民区的距离也相等,请你找到一个这样的点.
13.如图,∠ABC=60°,点D在AC上,ED=6,DE⊥BC,DF⊥AB,且DE=DF.
求:(1)∠ABD的度数.
(2)DB的长度.
14.如图,在△ABC中,BE⊥AC于点E,BC的垂直平分线分别交AB,BE于点D,G,垂足为H,CD⊥AB,CD交BE于点F.
(1)求证:△BDF≌△CDA,并写出BF与AC的数量关系.
(2)若DF=DG,求证:①BE平分∠ABC.②CE=BF.
【练素养】
15.如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F,交AC于点E,过点O作OD⊥BC于点D.
(1)求证:∠AOB=90°+∠C.
(2)求证:AE+BF=EF.
(3)若OD=a,CE+CF=2b,请用含a,b的代数式表示△CEF的面积,S△CEF= (直接写出结果).
参考答案
基础演练
1.A 2.D 3.A
4.BAD BCD
5.【解析】证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,∴AD平分∠BAC.
6.【解析】
证明:如图,过点D作DM⊥AB于点M,DN⊥AC于点N.∵△DCE的面积与△DBF的面积相等,
∴=.
∵CE=BF,∴DM=DN,
∴AD平分∠BAC.
能力生成
7.B 8.A 9.B 10.110 11.(2,2)或(1,-1)
12.【解析】点P到A,B两点的距离相等,根据性质:线段垂直平分线上的点到线段两个端点的距离相等.需用尺规作出线段AB的垂直平分线;点P到两相交直线CD,EF的距离相等,根据性质:角平分线上的点到角两边的距离相等.需用尺规作出∠COF的平分线,P为∠COF的平分线与线段AB的垂直平分线的交点.如图所示.
13.【解析】(1)∵DE⊥BC,DF⊥AB,
且DE=DF,
∴DB平分∠ABC,
即∠ABD=∠ABC=×60°=30°.
(2)在直角三角形BED中,
∵∠DBE=∠ABC=×60°=30°,
又∵DE=6,
∴BD=2DE=12.
14.【解析】证明:(1)∵DH垂直平分BC,
∴BD=CD.
∵BE⊥AC,BA⊥CD,
∴∠ADC=∠BDF=90°.
∵∠A+∠DBF=90°,∠DBF+∠DFB=90°,
∴∠A=∠DFB.
在△ADC和△FDB中,
∴△ADC≌△FDB(AAS),
∴BF=AC.
(2)①∵DF=DG,
∴∠DGF=∠DFG.
∵∠BGH=∠DGF,
∴∠BGH=∠DFG.
∵∠DBF+∠DFB=90°,∠FBC+∠BGH=90°,
∴∠DBF=∠FBC,
∴BE平分∠ABC.
②在△ABE和△CBE中,
∴△ABE≌△CBE(ASA),
∴AE=CE,
∴AC=2CE.
∵BF=AC,
∴CE=BF.
素养通关
15.【解析】(1)证明:∵OA,OB分别平分∠BAC和∠ABC,
∴∠OAB=∠OAE=∠BAC,∠OBA=∠OBF=∠ABC,
∴∠AOB=180°-∠OAB-∠OBA=180°-∠CAB-∠ABC=180°-(∠CAB+∠ABC)=180°-(180°-∠C)=90°+∠C.
(2)证明:∵EF∥AB,
∴∠OAB=∠AOE,∠ABO=∠BOF.
又∠OAB=∠EAO,∠OBA=∠OBF,
∴∠AOE=∠EAO,∠BOF=∠OBF,
∴AE=OE,BF=OF,
∴EF=OE+OF=AE+BF.
(3)ab.
提示:∵点O在∠ACB的平分线上,
∴点O到AC的距离等于OD,
∴S△CEF=(CE+CF)·OD=×2b·a=ab.
2
