第12章 一次函数 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 第12章 一次函数 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 392.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览



文档简介
第12章 一次函数 自我评估
(建议用时:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
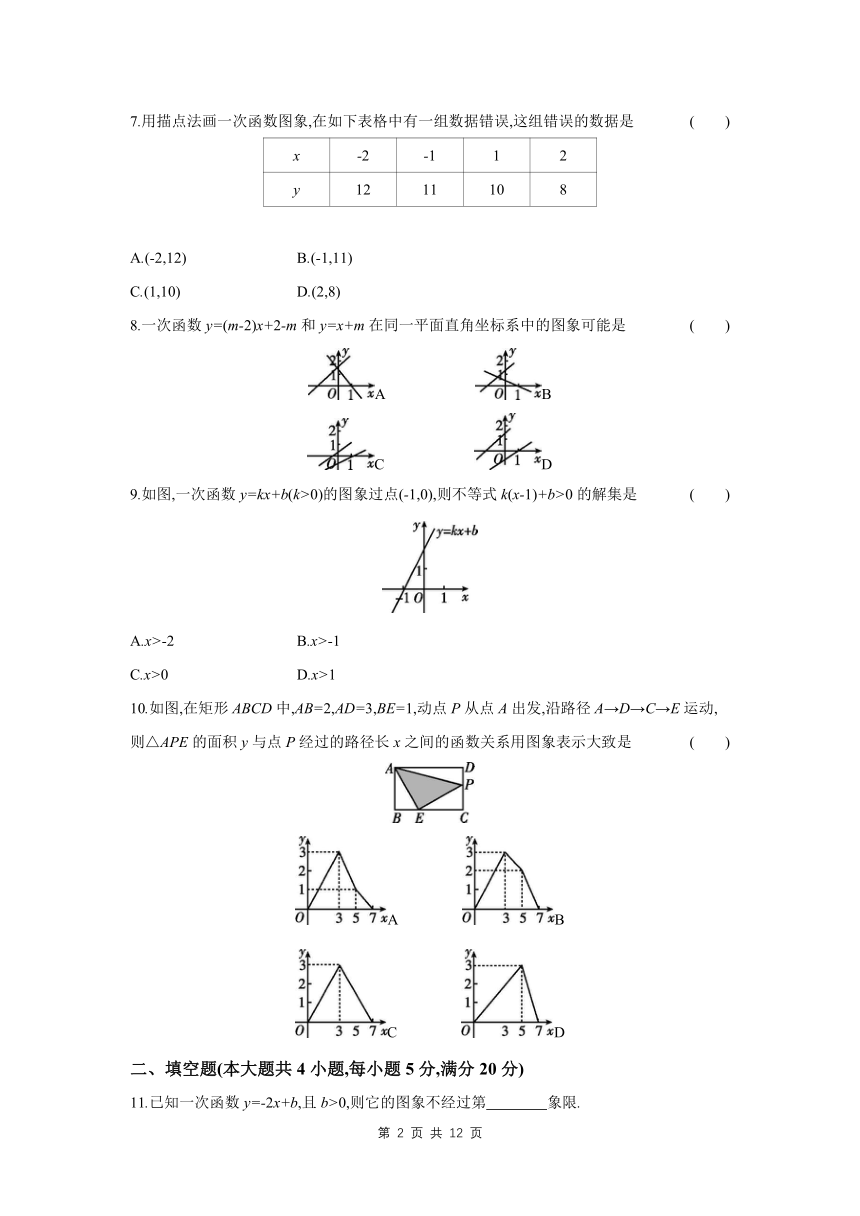
1.一次函数y=kx+b,经过(1,1),(2,4),则k与b的值为 ( )
A. B.
C. D.
2.若k>2,则一次函数y=(2-k)x+k-2的图象可能是 ( )
A B C D
3.某一次函数的图象与y轴交于正半轴,这个一次函数的表达式可能是 ( )
A.y=-2x B.y=-2x-2
C.y=-2x+2 D.y=2x-1
4.一次函数y=2x-4的图象是 ( )
A B
C D
5.在平面直角坐标系中,点A(2,-3)、B(4,3)、C(5,a)在同一条直线上,则a的值是 ( )
A.-6 B.6
C.6或3 D.6或-6
6.若一次函数y=(k-2)x+17,当x=-3时,y=2,则k的值为 ( )
A.-4 B.8 C.-3 D.7
7.用描点法画一次函数图象,在如下表格中有一组数据错误,这组错误的数据是 ( )
x -2 -1 1 2
y 12 11 10 8
A.(-2,12) B.(-1,11)
C.(1,10) D.(2,8)
8.一次函数y=(m-2)x+2-m和y=x+m在同一平面直角坐标系中的图象可能是 ( )
A B
C D
9.如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是 ( )
A.x>-2 B.x>-1
C.x>0 D.x>1
10.如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是 ( )
A B
C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知一次函数y=-2x+b,且b>0,则它的图象不经过第 象限.
12.已知函数y=kx的图象经过二、四象限,且函数不经过点(-1,1),请写出一个符合条件的函数解析式 .
13.周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B地.
14.甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图所示.
(1)在图中画出乙离A地的距离y2(单位:m)与时间x之间的函数图象.
(2)若甲比乙晚5 min到达B地,则甲整个行程所用的时间为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知y+3与x成正比例,且x=2时,y=1.求y关于x的函数表达式.
16.已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.
(1)求一次函数的表达式,并画出此一次函数的图象.
(2)求当x取何值时,函数值y>0.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,这是一个数据转换器的示意图,三个滚珠可以在槽内左右滚动.输入x的值,当滚珠发生撞击,就输出相撞滚珠上的代数式所表示数的和y.已知当三个滚珠同时相撞时,不论输入x的值为多大,输出y的值总不变.
(1)求a的值.
(2)若输入一个整数x,某些滚珠相撞,输出y值恰好为-1,求x的值.
18.求作y=x-2的图象.
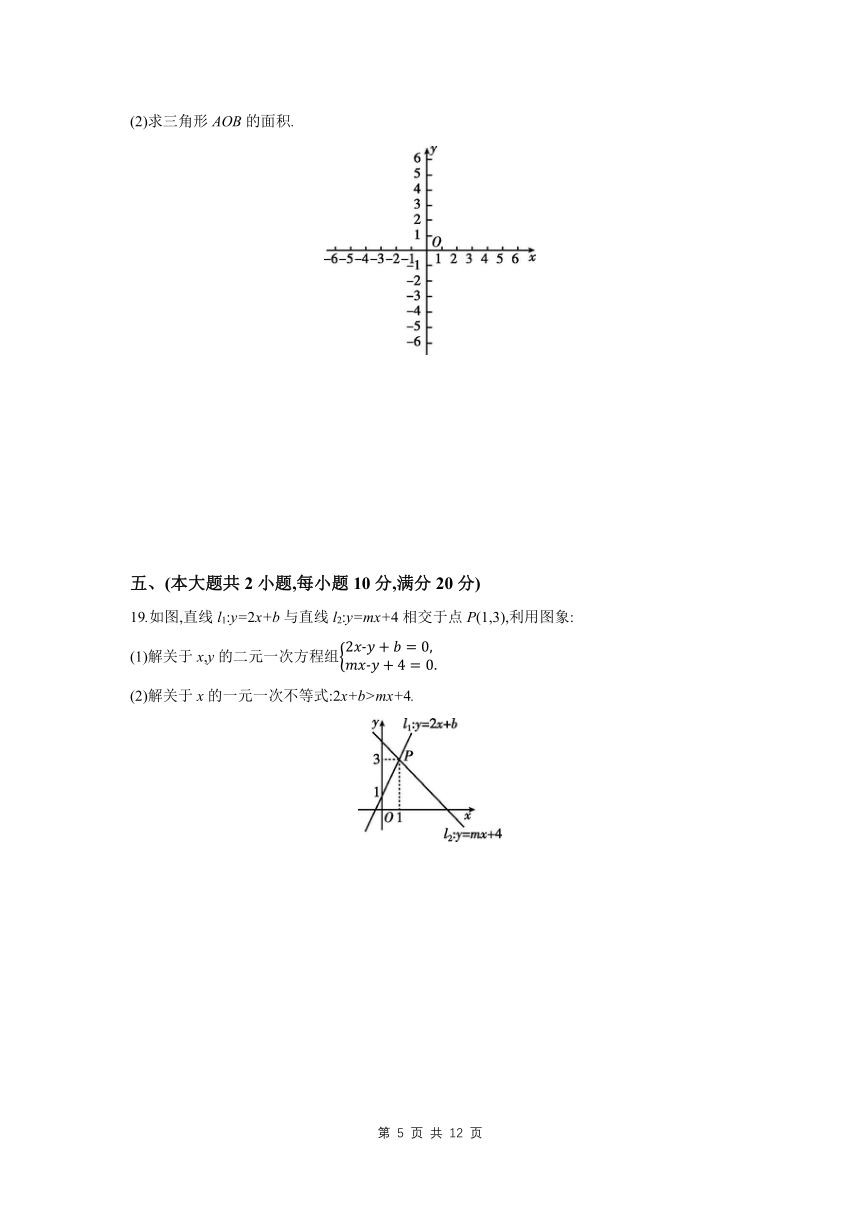
(1)写出与x轴、y轴的交点A,B的坐标.
(2)求三角形AOB的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,直线l1:y=2x+b与直线l2:y=mx+4相交于点P(1,3),利用图象:
(1)解关于x,y的二元一次方程组
(2)解关于x的一元一次不等式:2x+b>mx+4.
20.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,回答下列问题.
(1)填空:折线OABC表示 赛跑过程中的路程与时间的关系,线段OD表示 赛跑过程中的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑多少米 乌龟每分钟爬多少米
(3)乌龟用了多少分钟追上了正在睡觉的兔子
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡了多少分钟
六、(本题满分12分)
21.已知一次函数y=(3-m)x+m-4的图象不经过第一象限,且m为整数.
(1)求m的值.
(2)在给定的直角坐标系中画出该函数的图象.
(3)当-3七、(本题满分12分)
22.猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
类别 价格 A款玩偶 B款玩偶
进货价(元/个) 40 30
销售价(元/个) 56 45
(1)第一次小李用1100元购进了A,B两款玩偶共30个,问两款玩偶各购进多少个
(2)第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算 (注:利润率=×100%)
八、(本题满分14分)
23.为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
品种 进价 (元/斤) 售价(元/斤)
鲢鱼 a 5
草鱼 b 销量不超过200 斤的部分 销量超过 200斤的部分
8 7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)求a,b的值.
(2)老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼x斤(销售过程中损耗不计).
①分别求出每天销售鲢鱼获利y1(元),销售草鱼获利y2(元)与x之间的函数关系式,并写出x的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低m元,草鱼售价全部定为7元/斤,为了保证当天销售这两种鱼总获利W(元)最小值不少于320元,求m的最大值.
参考答案
1.A 2.D 3.C 4.A 5.B 6.D 7.C 8.B 9.C
10.B 11.三 12.y=-2x(答案不唯一) 13.12
14.【解析】(1)如图所示.
(2)12 min.
15.【解析】设y+3=kx(k是常数且k≠0),
将x=2,y=1代入y+3=kx得1+3=2k,
解得k=2,
∴y=2x-3.
16.【解析】(1)由题意得
解得
∴一次函数的表达式为y=x+2.
画出函数图象如图所示:
(2)由图象可知,当x>-2时,y>0.
17.【解析】(1)(2x-1)+3+ax=2x-1+3+ax=(2+a)x+2.
∵当三个滚珠同时相撞时,不论输入x的值为多大,输出y的值不变,
∴2+a=0,
解得a=-2.
答:a的值为-2.
(2)当y=2x-1+3=2x+2时,令y=-1,即-1=2x+2,
解得x=-1.5(不合题意,舍去);
当y=3+(-2x)=-2x+3时,令y=-1,即-1=-2x+3,
解得x=2.
答:x的值为2.
18.【解析】y=x-2图象如下图所示:
(1)A(2,0),B(0,-2).
(2)由图象可知:
△AOB为直角三角形,其中OA=OB=2,
∴S△AOB=OA·OB=×2×2=2.
19.【解析】(1)方程组的解可以看成一次函数y=2x+b与一次函数y=mx+4的交点的坐标P(1,3),
∴方程组的解
(2)观察图象可知,不等式的解集为x>1.
20.【解析】(1)兔子;乌龟;1500.
(2)由图象可知兔子在起初每分钟跑700米.
1500÷30=50(米),所以乌龟每分钟爬50米.
(3)700÷50=14(分钟),
所以乌龟用了14分钟追上了正在睡觉的兔子.
(4)48千米/时=800米/分钟,
(1500-700)÷800=1(分钟),
30+0.5-1×2=28.5(分钟),
∴兔子中间停下睡了28.5分钟.
21.【解析】(1)因为一次函数y=(3-m)x+m-4的图象不经过第一象限,m是整数,
可得
解得3∴m=4.
(2)∵m=4,
∴一次函数的解析式为y=-x,
该函数的图象如图所示.
(3)当-322.【解析】(1)设A款玩偶购进x个,B款玩偶购进(30-x)个,
由题意,得40x+30(30-x)=1100,
解得x=20.
30-20=10(个).
答:A款玩偶购进20个,B款玩偶购进10个.
(2)设A款玩偶购进a个,B款玩偶购进(30-a)个,获利y元,
由题意,得y=(56-40)a+(45-30)(30-a)=a+450.
∵A款玩偶进货数量不得超过B款玩偶进货数量的一半.
∴a≤(30-a),
∴a≤10.
∵y=a+450.
∴k=1>0,
∴y随a的增大而增大.
∴a=10时,y最大=460元.
此时B款玩偶为30-10=20(个).
答:按照A款玩偶购进10个、B款玩偶购进20个的方案进货才能获得最大利润,最大利润是460元.
(3)第一次的利润率=×100%≈42.7%,
第二次的利润率=×100%=46%.
∵46%>42.7%,
∴对于小李来说第二次的进货方案更合算.
23.【解析】(1)根据题意得
解得
(2)①由题意得y1=(5-3.5)x=1.5x(80≤x≤120),
当300-x≤200时,100≤x≤120,y2=(8-6)×(300-x)=-2x+600;
当300-x>200时,80≤x<100,y2=(8-6)×200+(7-6)×(300-x-200)=-x+500,
∴y2=
②由题意得W=(5-m-3.5)x+(7-6)×(300-x)=(0.5-m)x+300,其中80≤x≤120.
∵当0.5-m≤0时,W=(0.5-m)x+300≤300,不合题意,
∴0.5-m>0,
∴W随x的增大而增大,
∴当x=80时,W的值最小,
由题意得(0.5-m)×80+300≥320,
解得m≤0.25,
∴m的最大值为0.25.
(建议用时:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.一次函数y=kx+b,经过(1,1),(2,4),则k与b的值为 ( )
A. B.
C. D.
2.若k>2,则一次函数y=(2-k)x+k-2的图象可能是 ( )
A B C D
3.某一次函数的图象与y轴交于正半轴,这个一次函数的表达式可能是 ( )
A.y=-2x B.y=-2x-2
C.y=-2x+2 D.y=2x-1
4.一次函数y=2x-4的图象是 ( )
A B
C D
5.在平面直角坐标系中,点A(2,-3)、B(4,3)、C(5,a)在同一条直线上,则a的值是 ( )
A.-6 B.6
C.6或3 D.6或-6
6.若一次函数y=(k-2)x+17,当x=-3时,y=2,则k的值为 ( )
A.-4 B.8 C.-3 D.7
7.用描点法画一次函数图象,在如下表格中有一组数据错误,这组错误的数据是 ( )
x -2 -1 1 2
y 12 11 10 8
A.(-2,12) B.(-1,11)
C.(1,10) D.(2,8)
8.一次函数y=(m-2)x+2-m和y=x+m在同一平面直角坐标系中的图象可能是 ( )
A B
C D
9.如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是 ( )
A.x>-2 B.x>-1
C.x>0 D.x>1
10.如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是 ( )
A B
C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知一次函数y=-2x+b,且b>0,则它的图象不经过第 象限.
12.已知函数y=kx的图象经过二、四象限,且函数不经过点(-1,1),请写出一个符合条件的函数解析式 .
13.周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B地.
14.甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图所示.
(1)在图中画出乙离A地的距离y2(单位:m)与时间x之间的函数图象.
(2)若甲比乙晚5 min到达B地,则甲整个行程所用的时间为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知y+3与x成正比例,且x=2时,y=1.求y关于x的函数表达式.
16.已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.
(1)求一次函数的表达式,并画出此一次函数的图象.
(2)求当x取何值时,函数值y>0.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,这是一个数据转换器的示意图,三个滚珠可以在槽内左右滚动.输入x的值,当滚珠发生撞击,就输出相撞滚珠上的代数式所表示数的和y.已知当三个滚珠同时相撞时,不论输入x的值为多大,输出y的值总不变.
(1)求a的值.
(2)若输入一个整数x,某些滚珠相撞,输出y值恰好为-1,求x的值.
18.求作y=x-2的图象.
(1)写出与x轴、y轴的交点A,B的坐标.
(2)求三角形AOB的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,直线l1:y=2x+b与直线l2:y=mx+4相交于点P(1,3),利用图象:
(1)解关于x,y的二元一次方程组
(2)解关于x的一元一次不等式:2x+b>mx+4.
20.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,回答下列问题.
(1)填空:折线OABC表示 赛跑过程中的路程与时间的关系,线段OD表示 赛跑过程中的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑多少米 乌龟每分钟爬多少米
(3)乌龟用了多少分钟追上了正在睡觉的兔子
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡了多少分钟
六、(本题满分12分)
21.已知一次函数y=(3-m)x+m-4的图象不经过第一象限,且m为整数.
(1)求m的值.
(2)在给定的直角坐标系中画出该函数的图象.
(3)当-3
22.猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
类别 价格 A款玩偶 B款玩偶
进货价(元/个) 40 30
销售价(元/个) 56 45
(1)第一次小李用1100元购进了A,B两款玩偶共30个,问两款玩偶各购进多少个
(2)第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算 (注:利润率=×100%)
八、(本题满分14分)
23.为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
品种 进价 (元/斤) 售价(元/斤)
鲢鱼 a 5
草鱼 b 销量不超过200 斤的部分 销量超过 200斤的部分
8 7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)求a,b的值.
(2)老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼x斤(销售过程中损耗不计).
①分别求出每天销售鲢鱼获利y1(元),销售草鱼获利y2(元)与x之间的函数关系式,并写出x的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低m元,草鱼售价全部定为7元/斤,为了保证当天销售这两种鱼总获利W(元)最小值不少于320元,求m的最大值.
参考答案
1.A 2.D 3.C 4.A 5.B 6.D 7.C 8.B 9.C
10.B 11.三 12.y=-2x(答案不唯一) 13.12
14.【解析】(1)如图所示.
(2)12 min.
15.【解析】设y+3=kx(k是常数且k≠0),
将x=2,y=1代入y+3=kx得1+3=2k,
解得k=2,
∴y=2x-3.
16.【解析】(1)由题意得
解得
∴一次函数的表达式为y=x+2.
画出函数图象如图所示:
(2)由图象可知,当x>-2时,y>0.
17.【解析】(1)(2x-1)+3+ax=2x-1+3+ax=(2+a)x+2.
∵当三个滚珠同时相撞时,不论输入x的值为多大,输出y的值不变,
∴2+a=0,
解得a=-2.
答:a的值为-2.
(2)当y=2x-1+3=2x+2时,令y=-1,即-1=2x+2,
解得x=-1.5(不合题意,舍去);
当y=3+(-2x)=-2x+3时,令y=-1,即-1=-2x+3,
解得x=2.
答:x的值为2.
18.【解析】y=x-2图象如下图所示:
(1)A(2,0),B(0,-2).
(2)由图象可知:
△AOB为直角三角形,其中OA=OB=2,
∴S△AOB=OA·OB=×2×2=2.
19.【解析】(1)方程组的解可以看成一次函数y=2x+b与一次函数y=mx+4的交点的坐标P(1,3),
∴方程组的解
(2)观察图象可知,不等式的解集为x>1.
20.【解析】(1)兔子;乌龟;1500.
(2)由图象可知兔子在起初每分钟跑700米.
1500÷30=50(米),所以乌龟每分钟爬50米.
(3)700÷50=14(分钟),
所以乌龟用了14分钟追上了正在睡觉的兔子.
(4)48千米/时=800米/分钟,
(1500-700)÷800=1(分钟),
30+0.5-1×2=28.5(分钟),
∴兔子中间停下睡了28.5分钟.
21.【解析】(1)因为一次函数y=(3-m)x+m-4的图象不经过第一象限,m是整数,
可得
解得3
(2)∵m=4,
∴一次函数的解析式为y=-x,
该函数的图象如图所示.
(3)当-3
由题意,得40x+30(30-x)=1100,
解得x=20.
30-20=10(个).
答:A款玩偶购进20个,B款玩偶购进10个.
(2)设A款玩偶购进a个,B款玩偶购进(30-a)个,获利y元,
由题意,得y=(56-40)a+(45-30)(30-a)=a+450.
∵A款玩偶进货数量不得超过B款玩偶进货数量的一半.
∴a≤(30-a),
∴a≤10.
∵y=a+450.
∴k=1>0,
∴y随a的增大而增大.
∴a=10时,y最大=460元.
此时B款玩偶为30-10=20(个).
答:按照A款玩偶购进10个、B款玩偶购进20个的方案进货才能获得最大利润,最大利润是460元.
(3)第一次的利润率=×100%≈42.7%,
第二次的利润率=×100%=46%.
∵46%>42.7%,
∴对于小李来说第二次的进货方案更合算.
23.【解析】(1)根据题意得
解得
(2)①由题意得y1=(5-3.5)x=1.5x(80≤x≤120),
当300-x≤200时,100≤x≤120,y2=(8-6)×(300-x)=-2x+600;
当300-x>200时,80≤x<100,y2=(8-6)×200+(7-6)×(300-x-200)=-x+500,
∴y2=
②由题意得W=(5-m-3.5)x+(7-6)×(300-x)=(0.5-m)x+300,其中80≤x≤120.
∵当0.5-m≤0时,W=(0.5-m)x+300≤300,不合题意,
∴0.5-m>0,
∴W随x的增大而增大,
∴当x=80时,W的值最小,
由题意得(0.5-m)×80+300≥320,
解得m≤0.25,
∴m的最大值为0.25.
