第15章 轴对称图形与等腰三角形 课时作业(含答案) 2023-2024学年数学沪科版八年级上册
文档属性
| 名称 | 第15章 轴对称图形与等腰三角形 课时作业(含答案) 2023-2024学年数学沪科版八年级上册 | 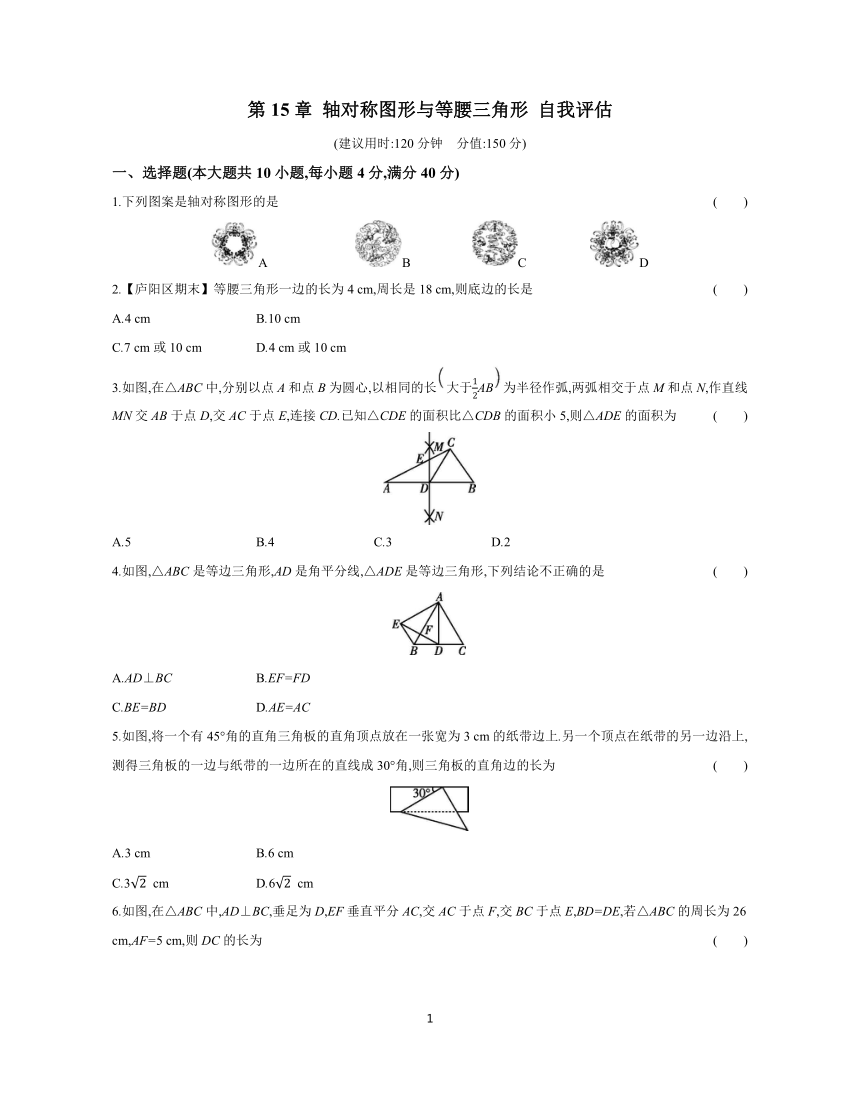 | |
| 格式 | docx | ||
| 文件大小 | 288.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:41:20 | ||
图片预览


文档简介
第15章 轴对称图形与等腰三角形 自我评估
(建议用时:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图案是轴对称图形的是 ( )
A B C D
2.【庐阳区期末】等腰三角形一边的长为4 cm,周长是18 cm,则底边的长是 ( )
A.4 cm B.10 cm
C.7 cm或10 cm D.4 cm或10 cm
3.如图,在△ABC中,分别以点A和点B为圆心,以相同的长大于AB为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为 ( )
A.5 B.4 C.3 D.2
4.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是 ( )
A.AD⊥BC B.EF=FD
C.BE=BD D.AE=AC
5.如图,将一个有45°角的直角三角板的直角顶点放在一张宽为3 cm的纸带边上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为 ( )
A.3 cm B.6 cm
C.3 cm D.6 cm
6.如图,在△ABC中,AD⊥BC,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,BD=DE,若△ABC的周长为26 cm,AF=5 cm,则DC的长为 ( )
A.8 cm B.7 cm
C.10 cm D.9 cm
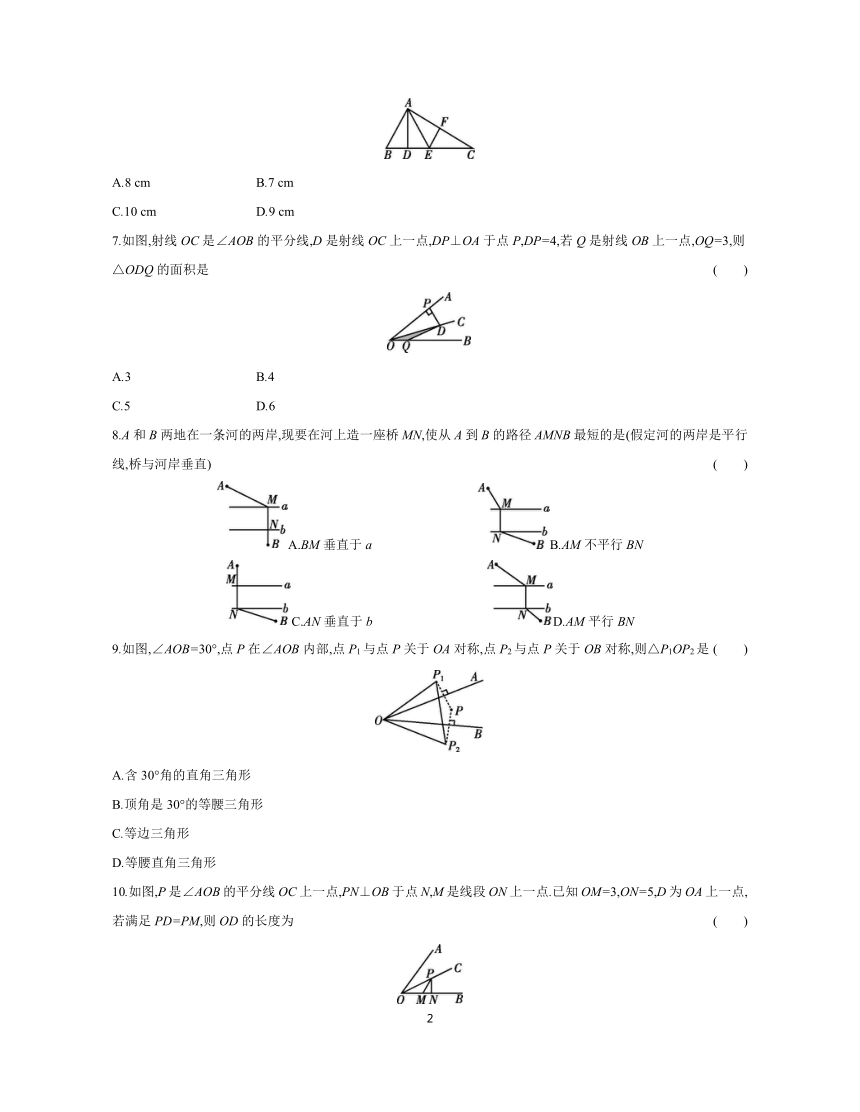
7.如图,射线OC是∠AOB的平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若Q是射线OB上一点,OQ=3,则△ODQ的面积是 ( )
A.3 B.4
C.5 D.6
8.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直) ( )
A.BM垂直于a B.AM不平行BN
C.AN垂直于b D.AM平行BN
9.如图,∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是 ( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
10.如图,P是∠AOB的平分线OC上一点,PN⊥OB于点N,M是线段ON上一点.已知OM=3,ON=5,D为OA上一点,若满足PD=PM,则OD的长度为 ( )
A.3 B.5 C.5和7 D.3和7
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC的角平分线CD交AB于点D,DE∥BC交AC于点E,若DE=4,AC=7,则AE= .
12.已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为 .
13.如图,等腰三角形ABC底边BC的长为4 cm,面积是12 cm2,D为BC边上的中点,腰AB的垂直平分线EF交AD于点M,交AC于点F,则BM+DM的值为 cm.
14.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,求灯塔与船之间的最近距离 海里.
16.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,AP+DP的最小值为 .
四、(本大题共2小题,每小题8分,满分16分)
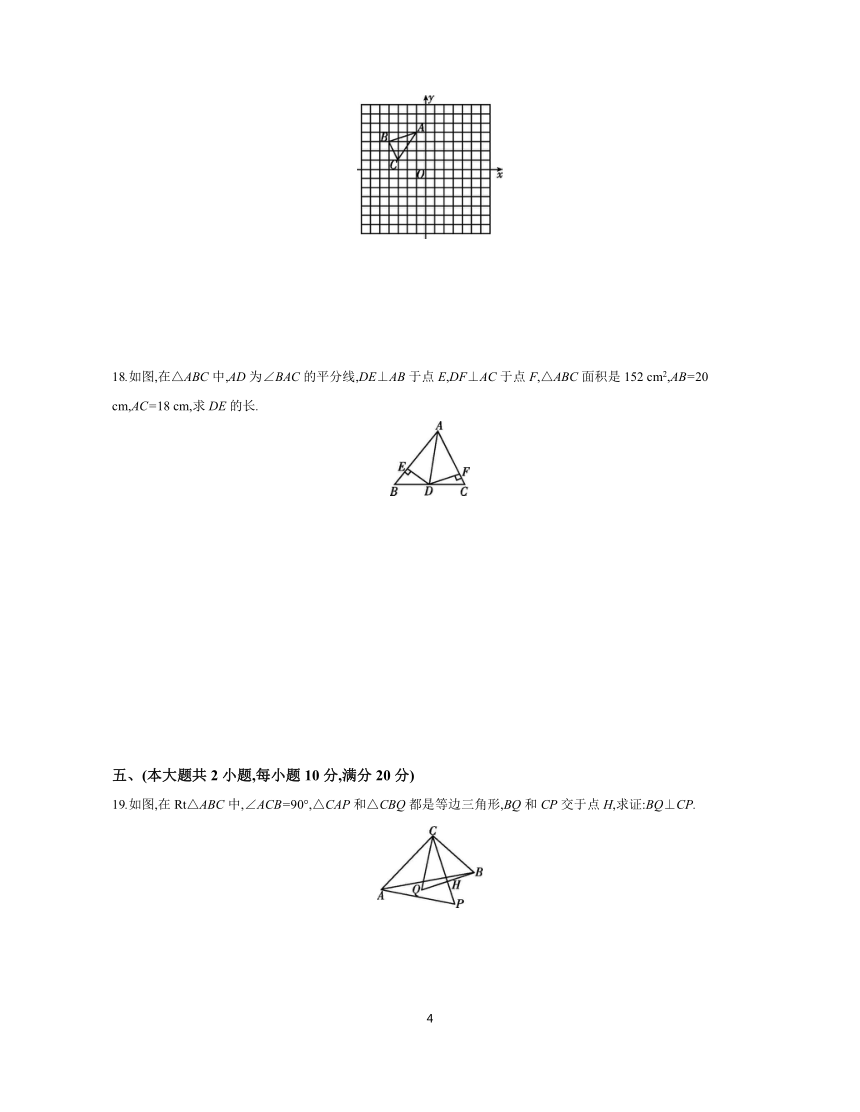
17.【庐阳区期末】如图,在边长为1个单位长度的小正方形方格中建立平面直角坐标系.已知△ABC的顶点A的坐标为A(-1,4),顶点B的坐标为(-4,3),顶点C的坐标为(-3,1).
(1)把△ABC向下平移4个单位长度,再以y轴为对称轴对称,得到△A'B'C',请你画出△A'B'C',并直接写出点A',B',C'的坐标.
(2)求△ABC的面积.
18.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是152 cm2,AB=20 cm,AC=18 cm,求DE的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在Rt△ABC中,∠ACB=90°,△CAP和△CBQ都是等边三角形,BQ和CP交于点H,求证:BQ⊥CP.
20.如图,在△ABC中,D为边BC上一点,AB=AD=CD.
(1)试说明∠ABC=2∠C.
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
六、(本题满分12分)
21.如图,射线AM是△ABC的外角∠NAC的平分线.
(1)作BC的垂直平分线PF,交射线AM于点P,交边BC于点F.(要求:尺规作图,保留作图痕迹,不必写作法和证明)
(2)过点P作PD⊥BA,PE⊥AC,垂足分别为D,E,请补全图形并证明BD=CE.
七、(本题满分12分)
22.如图,在△ABC中,∠ABC=45°,P为边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,△APC的PC边上的高为AH.
(1)求∠BPD的大小.
(2)判断直线BD,AH是否平行 并说明理由.
八、(本题满分14分)
23.如图,在等边△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形.
(2)若∠PAC=20°,求∠AEB的度数.
(3)连接CE,写出AE,BE,CE之间的数量关系,并证明你的结论.
参考答案
1.A 2.A 3.A 4.D 5.B 6.A 7.D 8.D 9.C
10.D 11.3 12.1 13.6 14.115° 15.10 16.16
17.【解析】(1)如图,△A'B'C'即为所求.
A'(1,0)、B'(4,-1)、C'(3,-3).
(2)△ABC的面积为3×3-×1×3-×1×2-×2×3=3.5.
18.【解析】∵AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF.
∵S△ABC=S△ABD+S△ACD,
∴S△ABC=×AB×DE+×AC×DF.
∵△ABC面积是152 cm2,AB=20 cm,AC=18 cm,
∴152=×20×DE+×18×DF,
∴10DE+9DF=152.
∵DE=DF,∴19DE=152,∴DE=8 cm.
19.【解析】证明:∵△CAP和△CBQ都是等边三角形,
∴∠ACP=∠CBQ=60°.
∵∠ACB=90°,
∴∠BCP=∠ACB-∠ACP=30°,
在△BCH中,∠BHC=180°-∠BCH-∠CBH=180°-30°-60°=90°,∴BQ⊥CP.
20.【解析】(1)∵AB=AD,∴∠ABC=∠ADB.
∵AD=CD,∴∠DAC=∠C.
∵∠ADB=∠DAC+∠C=2∠C,
∴∠ABC=2∠C.
(2)证明:∵AD平分∠BAC,∴∠DAB=∠CAD.
∵BE∥AD,
∴∠DAB=∠ABE,∠E=∠CAD,
∴∠ABE=∠E,∴AE=AB.
21.【解析】(1)如图,PF为所作.
(2)如图,连接PB、PC.
∵PF垂直平分BC,∴PB=PC.
∵AM是△ABC的外角∠NAC的平分线,PD⊥BA,PE⊥AC,∴PD=PE.
在Rt△BDP和Rt△CEP中,
∴Rt△BDP≌Rt△CEP(HL),∴BD=CE.
22.【解析】(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°.
∵点C关于直线PA的对称点为D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP,
∴∠APC=∠APD=60°,
∴∠BPD=180°-120°=60°.
(2)直线BD,AH平行.
理由:∵BC=3BP,∴BP=PC=PD.
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,∴∠BEP=60°,
∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,∴BD∥AH.
23.【解析】(1)图形如图1所示.
(2)在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠PAC=∠PAD,∴AB=AD,
∴∠ABD=∠D.
∵∠PAC=20°,∴∠PAD=20°,
∴∠BAD=∠BAC+∠PAC+∠PAD=100°,
∴∠D=(180°-∠BAD)=40°,
∴∠AEB=∠D+∠PAD=60°.
(3)结论:CE+AE=BE.
理由:如图2,在BE上取点M使ME=AE,在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠EAC=∠EAD,设∠EAC=∠DAE=x.
∵AD=AC=AB,
∴∠D=(180°-∠BAC-2x)=60°-x,
∴∠AEB=∠D+∠DAE=60°-x+x=60°,
∴△AME为等边三角形,
∴∠MAE=∠BAC=60°,
∴∠BAM=∠CAE.
在△AEC和△AMB中,
∴△AEC≌△AMB(SAS),∴CE=BM,
∴CE+AE=BM+ME=BE.
2
(建议用时:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图案是轴对称图形的是 ( )
A B C D
2.【庐阳区期末】等腰三角形一边的长为4 cm,周长是18 cm,则底边的长是 ( )
A.4 cm B.10 cm
C.7 cm或10 cm D.4 cm或10 cm
3.如图,在△ABC中,分别以点A和点B为圆心,以相同的长大于AB为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为 ( )
A.5 B.4 C.3 D.2
4.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是 ( )
A.AD⊥BC B.EF=FD
C.BE=BD D.AE=AC
5.如图,将一个有45°角的直角三角板的直角顶点放在一张宽为3 cm的纸带边上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为 ( )
A.3 cm B.6 cm
C.3 cm D.6 cm
6.如图,在△ABC中,AD⊥BC,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,BD=DE,若△ABC的周长为26 cm,AF=5 cm,则DC的长为 ( )
A.8 cm B.7 cm
C.10 cm D.9 cm
7.如图,射线OC是∠AOB的平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若Q是射线OB上一点,OQ=3,则△ODQ的面积是 ( )
A.3 B.4
C.5 D.6
8.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直) ( )
A.BM垂直于a B.AM不平行BN
C.AN垂直于b D.AM平行BN
9.如图,∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是 ( )
A.含30°角的直角三角形
B.顶角是30°的等腰三角形
C.等边三角形
D.等腰直角三角形
10.如图,P是∠AOB的平分线OC上一点,PN⊥OB于点N,M是线段ON上一点.已知OM=3,ON=5,D为OA上一点,若满足PD=PM,则OD的长度为 ( )
A.3 B.5 C.5和7 D.3和7
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC的角平分线CD交AB于点D,DE∥BC交AC于点E,若DE=4,AC=7,则AE= .
12.已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为 .
13.如图,等腰三角形ABC底边BC的长为4 cm,面积是12 cm2,D为BC边上的中点,腰AB的垂直平分线EF交AD于点M,交AC于点F,则BM+DM的值为 cm.
14.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,求灯塔与船之间的最近距离 海里.
16.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,AP+DP的最小值为 .
四、(本大题共2小题,每小题8分,满分16分)
17.【庐阳区期末】如图,在边长为1个单位长度的小正方形方格中建立平面直角坐标系.已知△ABC的顶点A的坐标为A(-1,4),顶点B的坐标为(-4,3),顶点C的坐标为(-3,1).
(1)把△ABC向下平移4个单位长度,再以y轴为对称轴对称,得到△A'B'C',请你画出△A'B'C',并直接写出点A',B',C'的坐标.
(2)求△ABC的面积.
18.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是152 cm2,AB=20 cm,AC=18 cm,求DE的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在Rt△ABC中,∠ACB=90°,△CAP和△CBQ都是等边三角形,BQ和CP交于点H,求证:BQ⊥CP.
20.如图,在△ABC中,D为边BC上一点,AB=AD=CD.
(1)试说明∠ABC=2∠C.
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
六、(本题满分12分)
21.如图,射线AM是△ABC的外角∠NAC的平分线.
(1)作BC的垂直平分线PF,交射线AM于点P,交边BC于点F.(要求:尺规作图,保留作图痕迹,不必写作法和证明)
(2)过点P作PD⊥BA,PE⊥AC,垂足分别为D,E,请补全图形并证明BD=CE.
七、(本题满分12分)
22.如图,在△ABC中,∠ABC=45°,P为边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,△APC的PC边上的高为AH.
(1)求∠BPD的大小.
(2)判断直线BD,AH是否平行 并说明理由.
八、(本题满分14分)
23.如图,在等边△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形.
(2)若∠PAC=20°,求∠AEB的度数.
(3)连接CE,写出AE,BE,CE之间的数量关系,并证明你的结论.
参考答案
1.A 2.A 3.A 4.D 5.B 6.A 7.D 8.D 9.C
10.D 11.3 12.1 13.6 14.115° 15.10 16.16
17.【解析】(1)如图,△A'B'C'即为所求.
A'(1,0)、B'(4,-1)、C'(3,-3).
(2)△ABC的面积为3×3-×1×3-×1×2-×2×3=3.5.
18.【解析】∵AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF.
∵S△ABC=S△ABD+S△ACD,
∴S△ABC=×AB×DE+×AC×DF.
∵△ABC面积是152 cm2,AB=20 cm,AC=18 cm,
∴152=×20×DE+×18×DF,
∴10DE+9DF=152.
∵DE=DF,∴19DE=152,∴DE=8 cm.
19.【解析】证明:∵△CAP和△CBQ都是等边三角形,
∴∠ACP=∠CBQ=60°.
∵∠ACB=90°,
∴∠BCP=∠ACB-∠ACP=30°,
在△BCH中,∠BHC=180°-∠BCH-∠CBH=180°-30°-60°=90°,∴BQ⊥CP.
20.【解析】(1)∵AB=AD,∴∠ABC=∠ADB.
∵AD=CD,∴∠DAC=∠C.
∵∠ADB=∠DAC+∠C=2∠C,
∴∠ABC=2∠C.
(2)证明:∵AD平分∠BAC,∴∠DAB=∠CAD.
∵BE∥AD,
∴∠DAB=∠ABE,∠E=∠CAD,
∴∠ABE=∠E,∴AE=AB.
21.【解析】(1)如图,PF为所作.
(2)如图,连接PB、PC.
∵PF垂直平分BC,∴PB=PC.
∵AM是△ABC的外角∠NAC的平分线,PD⊥BA,PE⊥AC,∴PD=PE.
在Rt△BDP和Rt△CEP中,
∴Rt△BDP≌Rt△CEP(HL),∴BD=CE.
22.【解析】(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°.
∵点C关于直线PA的对称点为D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP,
∴∠APC=∠APD=60°,
∴∠BPD=180°-120°=60°.
(2)直线BD,AH平行.
理由:∵BC=3BP,∴BP=PC=PD.
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,∴∠BEP=60°,
∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,∴BD∥AH.
23.【解析】(1)图形如图1所示.
(2)在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠PAC=∠PAD,∴AB=AD,
∴∠ABD=∠D.
∵∠PAC=20°,∴∠PAD=20°,
∴∠BAD=∠BAC+∠PAC+∠PAD=100°,
∴∠D=(180°-∠BAD)=40°,
∴∠AEB=∠D+∠PAD=60°.
(3)结论:CE+AE=BE.
理由:如图2,在BE上取点M使ME=AE,在等边△ABC中,AC=AB,∠BAC=60°,由对称可知:AC=AD,∠EAC=∠EAD,设∠EAC=∠DAE=x.
∵AD=AC=AB,
∴∠D=(180°-∠BAC-2x)=60°-x,
∴∠AEB=∠D+∠DAE=60°-x+x=60°,
∴△AME为等边三角形,
∴∠MAE=∠BAC=60°,
∴∠BAM=∠CAE.
在△AEC和△AMB中,
∴△AEC≌△AMB(SAS),∴CE=BM,
∴CE+AE=BM+ME=BE.
2
