2024年河南省郑州市中考模拟数学试卷(四)(含答案)
文档属性
| 名称 | 2024年河南省郑州市中考模拟数学试卷(四)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 683.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 18:05:15 | ||
图片预览

文档简介
2023-2024下学期河南省郑州市中考模拟数学试卷(四)
考试时间:100分钟 满分:120分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前1分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个正确的。
得分
1.有理数 的相反数是( )
A.2 B. C.-2 D.
2.2006年,我市深入实施环境污染整治,某经济开发区的40家化工企业中已关停,整改32家,每年排放的污水减少了167 000吨.将167 000用科学记数法表示为( )
A.167×103 B.16.7×104 C.1.67×105 D.0.167×106
3.右图是某几何体的视图,则该几何体是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
4.计算:的值是( )
A.0 B.1 C.2 D.3
5. ABCD中,∠A比∠B小20°,则∠A的度数为( )
A.60° B.80° C.100° D.120°
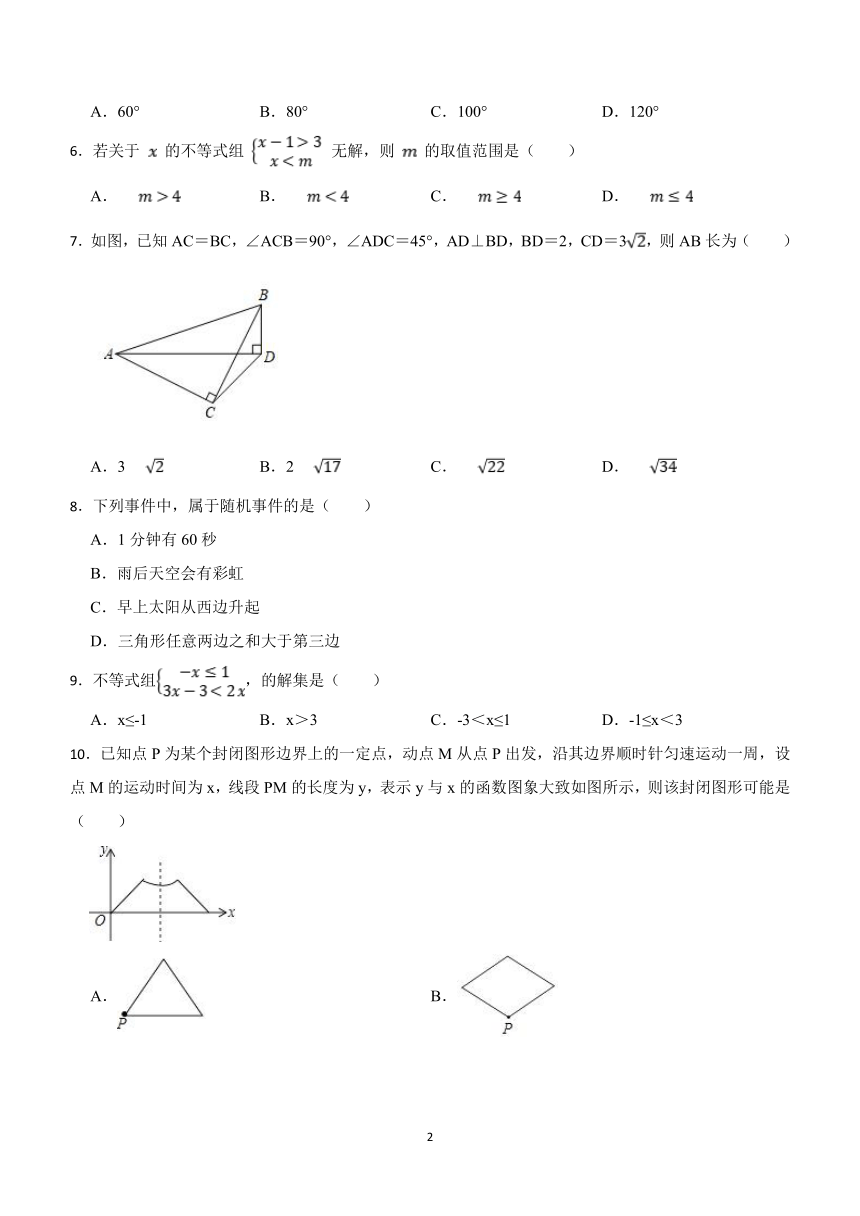
6.若关于 的不等式组 无解,则 的取值范围是( )
A. B. C. D.
7.如图,已知AC=BC,∠ACB=90°,∠ADC=45°,AD⊥BD,BD=2,CD=3,则AB长为( )
A.3 B.2 C. D.
8.下列事件中,属于随机事件的是( )
A.1分钟有60秒
B.雨后天空会有彩虹
C.早上太阳从西边升起
D.三角形任意两边之和大于第三边
9.不等式组,的解集是( )
A.x≤-1 B.x>3 C.-3<x≤1 D.-1≤x<3
10.已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. B.
C. D.
阅卷人 二、填空题(每小题3分,共15分)
得分
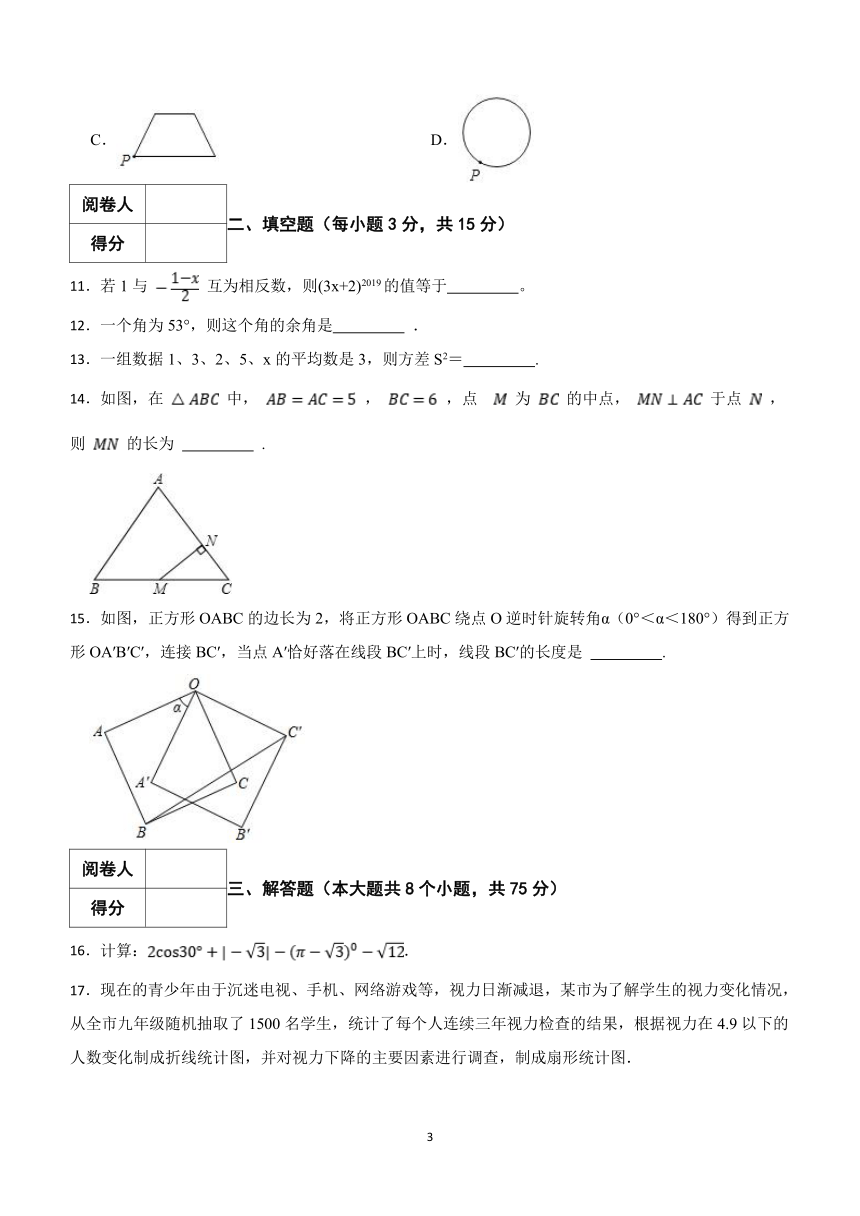
11.若1与 互为相反数,则(3x+2)2019的值等于 。
12.一个角为53°,则这个角的余角是 .
13.一组数据1、3、2、5、x的平均数是3,则方差S2= .
14.如图,在 中, , ,点 为 的中点, 于点 ,则 的长为 .
15.如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
阅卷人 三、解答题(本大题共8个小题,共75分)
得分
16.计算:.
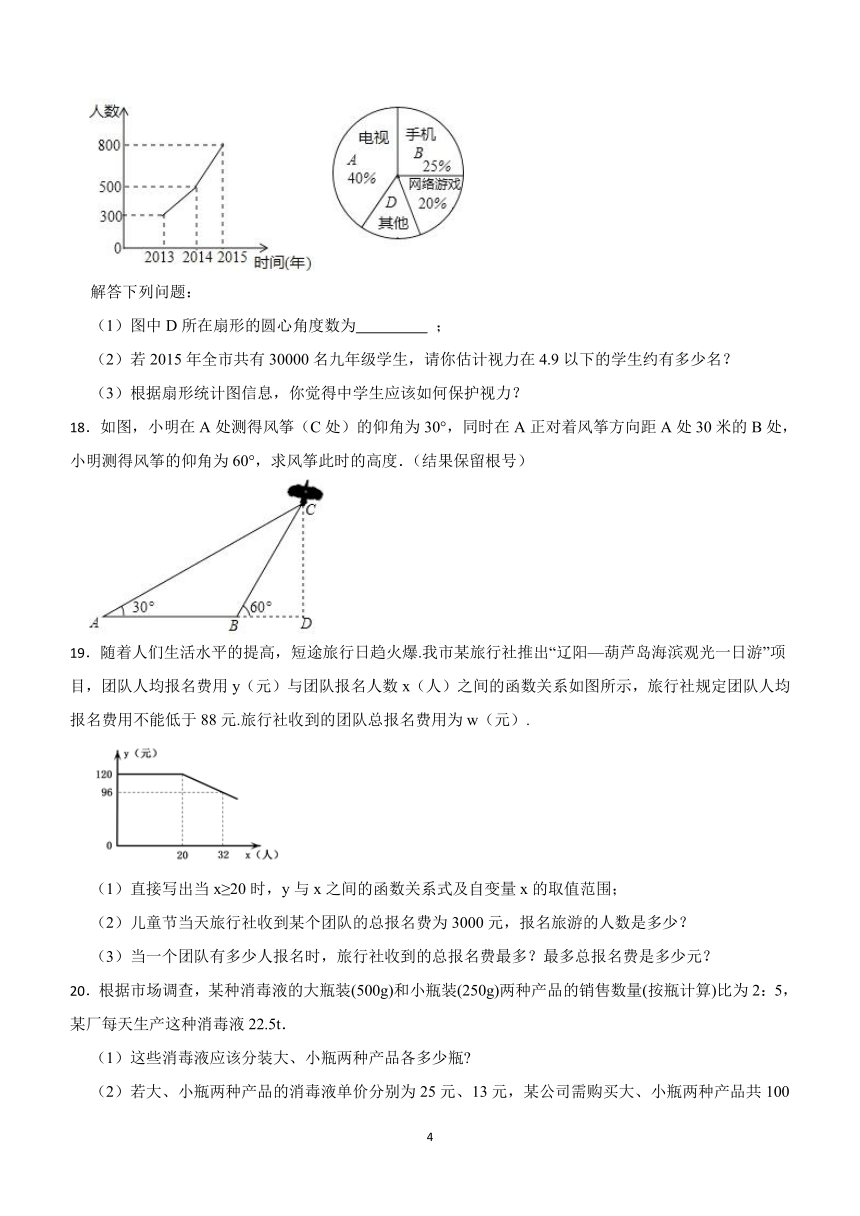
17.现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
解答下列问题:
(1)图中D所在扇形的圆心角度数为 ;
(2)若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
18.如图,小明在A处测得风筝(C处)的仰角为30°,同时在A正对着风筝方向距A处30米的B处,小明测得风筝的仰角为60°,求风筝此时的高度.(结果保留根号)
19.随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
20.根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5,某厂每天生产这种消毒液22.5t.
(1)这些消毒液应该分装大、小瓶两种产品各多少瓶
(2)若大、小瓶两种产品的消毒液单价分别为25元、13元,某公司需购买大、小瓶两种产品共100瓶,且购置费不多于1660元,则大瓶的消毒液最多购买多少瓶
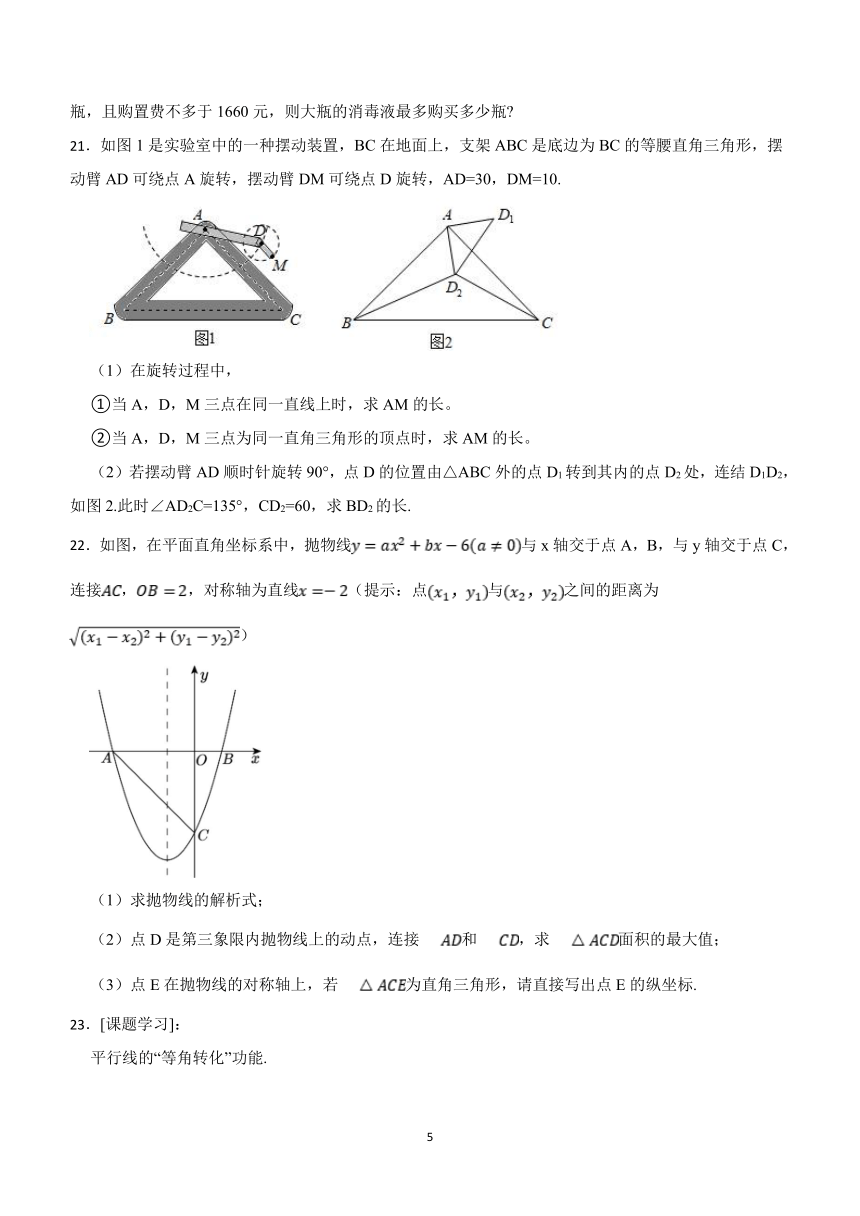
21.如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2.此时∠AD2C=135°,CD2=60,求BD2的长.
22.如图,在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,连接,,对称轴为直线(提示:点与之间的距离为)
(1)求抛物线的解析式;
(2)点D是第三象限内抛物线上的动点,连接和,求面积的最大值;
(3)点E在抛物线的对称轴上,若为直角三角形,请直接写出点E的纵坐标.
23.[课题学习]:
平行线的“等角转化”功能.
(1)[阅读理解]:
如图1,已知点是外一点,连接,,求的度数.
阅读并补充下面推理过程.
解:过点作,所以 ,
又因为
所以
(2)[方法运用]:
如图2,已知,求的度数.
(3)[深化拓展]:
已知,点在的右侧,,平分,平分,,所在的直线交于点,点在与两条平行线之间.
①如图3,若,则 °
②如图4,点在点的右侧,若,则 °(用含的代数式表示)
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】D
10.【答案】A
11.【答案】-1
12.【答案】37°
13.【答案】2
14.【答案】
15.【答案】
16.【答案】解:原式=
=
=-1.
17.【答案】(1)54°
(2)【解答】解:
根据题意得:30000×=16000(名),
则估计视力在4.9以下的学生约有16000名;
(3)建议中学生应少看电视,少玩游戏,少看手机,才能保护视力.
18.【答案】解:∵∠A=30°,∠CBD=60°,∴∠ACB=30°,∴BC=AB=30米,在Rt△BCD中,∠CBD=60°,BC=30,∴sin∠CBD= ,sin60°= ,∴CD=15 米,答:风筝此时的高度15 米
19.【答案】(1)解:设y=kx+b,
把(20,120)和(32,96)代入得: ,
解得: ,
y与x之间的函数关系式为:y=-2x+160;
∵旅行社规定团队人均报名费用不能低于88元,
当y≥88时,-2x+160≥88,
x≤36,
∴y与x之间的函数关系式为:y=-2x+160(20≤x≤36);
(2)解:20×120=2400<3000,
由题意得:w=xy=x(-2x+160)=3000,
-2x2+160x-3000=0,
x2-80x+1500=0,
(x-50)(x-30)=0,
x=50或30,
当x=50时,y= =60,不符合题意,舍去,
当x=30时,y= =100>88,符合题意,
答:报名旅游的人数是30人;
(3)解:w=xy=x(-2x+160)=-2x2+160x=-2(x2-80x+1600-1600)=-2(x-40)2+3200,
∵-2<0,
∴x<40,w随x的增大而增大,
∵x=36时,w有最大值为:-2(36-40)2+3200=3168,
∴当一个团队有36人报名时,旅行社收到的总报名费最多,最多总报名费是3168元
20.【答案】(1)解:设这些消毒液应该分装大瓶产品x瓶,小瓶产品y瓶
由题意得:
解得
答:这些消毒液应该分装大瓶产品20000瓶,小瓶产品50000瓶;
(2)解:设大瓶的消毒液购买a瓶,则小瓶的消毒液购买 瓶
由题意得:
解得
故大瓶的消毒液最多购买30瓶.
21.【答案】(1)解:①AM=AD+DM=40,或AM=AD-DM=20.
②显然∠MAD不能为直角。
当∠AMD为直角时
AM2=AD2-DM2=302-102=800,∴AM=20
当∠ADM为直角时,
AM2=AD2+CM2=302+102=1000 ∴AM=10
(2)解:连结CD1由题意得∠D1AD2=90°,
AD1=AD2=30
∴∠AD2D1=45°,D1D2=30
又∵∠AD2C=135°,∴∠CD2D1=90°
∴CD1= =30
∵∠BAC=∠D2AD1=90°
∴即∠BAD2=∠CAD1
又∵AB=AC,AD1=AD2, ∴△ABD2≌△ACD1
∴BD2=CD1=30
22.【答案】(1)解:∵,
∴,
∵对称轴为,
∴,
将A,B代入解析式得:
,
解得,
∴
(2)解:令时,则,
∴,
∵,,
∴设直线的解析式为:,
即:,解得,
∴直线的解析式为:,
设点,
作轴交于点F,如图,
则,
∴,
∴,
化成顶点式:,
当时,有最大值为;
(3)解:、、-8或4
23.【答案】(1)∠BAE;∠DAC[解题反思]:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将,,“凑”在一起,得到角的关系,使问题得到解决.
(2)证明:过C作CM∥AB
∴∠B=∠BCM
又∵AB∥ED
∴ED∥CM
∴∠D=∠DCM
又知:∠BCM+∠DCM+∠BCD=360°
∴∠B+∠BCD+∠D=360°
(3)65°;35°+180°-=215°-
考试时间:100分钟 满分:120分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前1分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个正确的。
得分
1.有理数 的相反数是( )
A.2 B. C.-2 D.
2.2006年,我市深入实施环境污染整治,某经济开发区的40家化工企业中已关停,整改32家,每年排放的污水减少了167 000吨.将167 000用科学记数法表示为( )
A.167×103 B.16.7×104 C.1.67×105 D.0.167×106
3.右图是某几何体的视图,则该几何体是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
4.计算:的值是( )
A.0 B.1 C.2 D.3
5. ABCD中,∠A比∠B小20°,则∠A的度数为( )
A.60° B.80° C.100° D.120°
6.若关于 的不等式组 无解,则 的取值范围是( )
A. B. C. D.
7.如图,已知AC=BC,∠ACB=90°,∠ADC=45°,AD⊥BD,BD=2,CD=3,则AB长为( )
A.3 B.2 C. D.
8.下列事件中,属于随机事件的是( )
A.1分钟有60秒
B.雨后天空会有彩虹
C.早上太阳从西边升起
D.三角形任意两边之和大于第三边
9.不等式组,的解集是( )
A.x≤-1 B.x>3 C.-3<x≤1 D.-1≤x<3
10.已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. B.
C. D.
阅卷人 二、填空题(每小题3分,共15分)
得分
11.若1与 互为相反数,则(3x+2)2019的值等于 。
12.一个角为53°,则这个角的余角是 .
13.一组数据1、3、2、5、x的平均数是3,则方差S2= .
14.如图,在 中, , ,点 为 的中点, 于点 ,则 的长为 .
15.如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
阅卷人 三、解答题(本大题共8个小题,共75分)
得分
16.计算:.
17.现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
解答下列问题:
(1)图中D所在扇形的圆心角度数为 ;
(2)若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
18.如图,小明在A处测得风筝(C处)的仰角为30°,同时在A正对着风筝方向距A处30米的B处,小明测得风筝的仰角为60°,求风筝此时的高度.(结果保留根号)
19.随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
20.根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5,某厂每天生产这种消毒液22.5t.
(1)这些消毒液应该分装大、小瓶两种产品各多少瓶
(2)若大、小瓶两种产品的消毒液单价分别为25元、13元,某公司需购买大、小瓶两种产品共100瓶,且购置费不多于1660元,则大瓶的消毒液最多购买多少瓶
21.如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2.此时∠AD2C=135°,CD2=60,求BD2的长.
22.如图,在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,连接,,对称轴为直线(提示:点与之间的距离为)
(1)求抛物线的解析式;
(2)点D是第三象限内抛物线上的动点,连接和,求面积的最大值;
(3)点E在抛物线的对称轴上,若为直角三角形,请直接写出点E的纵坐标.
23.[课题学习]:
平行线的“等角转化”功能.
(1)[阅读理解]:
如图1,已知点是外一点,连接,,求的度数.
阅读并补充下面推理过程.
解:过点作,所以 ,
又因为
所以
(2)[方法运用]:
如图2,已知,求的度数.
(3)[深化拓展]:
已知,点在的右侧,,平分,平分,,所在的直线交于点,点在与两条平行线之间.
①如图3,若,则 °
②如图4,点在点的右侧,若,则 °(用含的代数式表示)
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】D
10.【答案】A
11.【答案】-1
12.【答案】37°
13.【答案】2
14.【答案】
15.【答案】
16.【答案】解:原式=
=
=-1.
17.【答案】(1)54°
(2)【解答】解:
根据题意得:30000×=16000(名),
则估计视力在4.9以下的学生约有16000名;
(3)建议中学生应少看电视,少玩游戏,少看手机,才能保护视力.
18.【答案】解:∵∠A=30°,∠CBD=60°,∴∠ACB=30°,∴BC=AB=30米,在Rt△BCD中,∠CBD=60°,BC=30,∴sin∠CBD= ,sin60°= ,∴CD=15 米,答:风筝此时的高度15 米
19.【答案】(1)解:设y=kx+b,
把(20,120)和(32,96)代入得: ,
解得: ,
y与x之间的函数关系式为:y=-2x+160;
∵旅行社规定团队人均报名费用不能低于88元,
当y≥88时,-2x+160≥88,
x≤36,
∴y与x之间的函数关系式为:y=-2x+160(20≤x≤36);
(2)解:20×120=2400<3000,
由题意得:w=xy=x(-2x+160)=3000,
-2x2+160x-3000=0,
x2-80x+1500=0,
(x-50)(x-30)=0,
x=50或30,
当x=50时,y= =60,不符合题意,舍去,
当x=30时,y= =100>88,符合题意,
答:报名旅游的人数是30人;
(3)解:w=xy=x(-2x+160)=-2x2+160x=-2(x2-80x+1600-1600)=-2(x-40)2+3200,
∵-2<0,
∴x<40,w随x的增大而增大,
∵x=36时,w有最大值为:-2(36-40)2+3200=3168,
∴当一个团队有36人报名时,旅行社收到的总报名费最多,最多总报名费是3168元
20.【答案】(1)解:设这些消毒液应该分装大瓶产品x瓶,小瓶产品y瓶
由题意得:
解得
答:这些消毒液应该分装大瓶产品20000瓶,小瓶产品50000瓶;
(2)解:设大瓶的消毒液购买a瓶,则小瓶的消毒液购买 瓶
由题意得:
解得
故大瓶的消毒液最多购买30瓶.
21.【答案】(1)解:①AM=AD+DM=40,或AM=AD-DM=20.
②显然∠MAD不能为直角。
当∠AMD为直角时
AM2=AD2-DM2=302-102=800,∴AM=20
当∠ADM为直角时,
AM2=AD2+CM2=302+102=1000 ∴AM=10
(2)解:连结CD1由题意得∠D1AD2=90°,
AD1=AD2=30
∴∠AD2D1=45°,D1D2=30
又∵∠AD2C=135°,∴∠CD2D1=90°
∴CD1= =30
∵∠BAC=∠D2AD1=90°
∴
又∵AB=AC,AD1=AD2, ∴△ABD2≌△ACD1
∴BD2=CD1=30
22.【答案】(1)解:∵,
∴,
∵对称轴为,
∴,
将A,B代入解析式得:
,
解得,
∴
(2)解:令时,则,
∴,
∵,,
∴设直线的解析式为:,
即:,解得,
∴直线的解析式为:,
设点,
作轴交于点F,如图,
则,
∴,
∴,
化成顶点式:,
当时,有最大值为;
(3)解:、、-8或4
23.【答案】(1)∠BAE;∠DAC[解题反思]:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将,,“凑”在一起,得到角的关系,使问题得到解决.
(2)证明:过C作CM∥AB
∴∠B=∠BCM
又∵AB∥ED
∴ED∥CM
∴∠D=∠DCM
又知:∠BCM+∠DCM+∠BCD=360°
∴∠B+∠BCD+∠D=360°
(3)65°;35°+180°-=215°-
同课章节目录
