第1-2单元质量调研卷-数学五年级下册北师大版(含解析)
文档属性
| 名称 | 第1-2单元质量调研卷-数学五年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 519.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 20:51:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-2单元质量调研卷-数学五年级下册北师大版
一、选择题
1.淘气看一本书,第一天看了全书的,第二天要看这本书的( ),才能保证两天正好看完这本书的一半。
A. B. C. D.
2.甲、乙两人进行百米赛跑,甲用了分,乙用了0.3分,( )跑得快一些。
A.甲 B.乙 C.一样快 D.无法比较
3.下面各题中“2”和“5”可以直接相加的算式是( )。
A.230+675 B.2+ C.0.26+2.573 D.+
4.3个小正方体并排摆在空地上,露在外面的面有( )。
A.3个 B.9个 C.11个 D.14个
5.一块长方体木料横截面的面积是,李师傅要把它沿横截面截成三段,表面积增加( )。
A. B. C. D.
6.如图,在棱长为2cm的正方体上截去一个棱长为1cm的小正方体。表面积与原来比,( )。
A.变大了 B.变小了 C.不变 D.无法确定
二、填空题
7.(填小数)。
8.把转化为小数,这个小数的小数点后第2023位的数字是( )。
9.已知是最简真分数,那么符合条件的所有真分数的和是( )。
10.一个长方体框架,长5厘米,宽4厘米,高3厘米,做这个框架共要( )厘米的铁丝;若在它的表面贴上塑料板,共要( )平方厘米塑料板。
11.把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是( ) cm2。
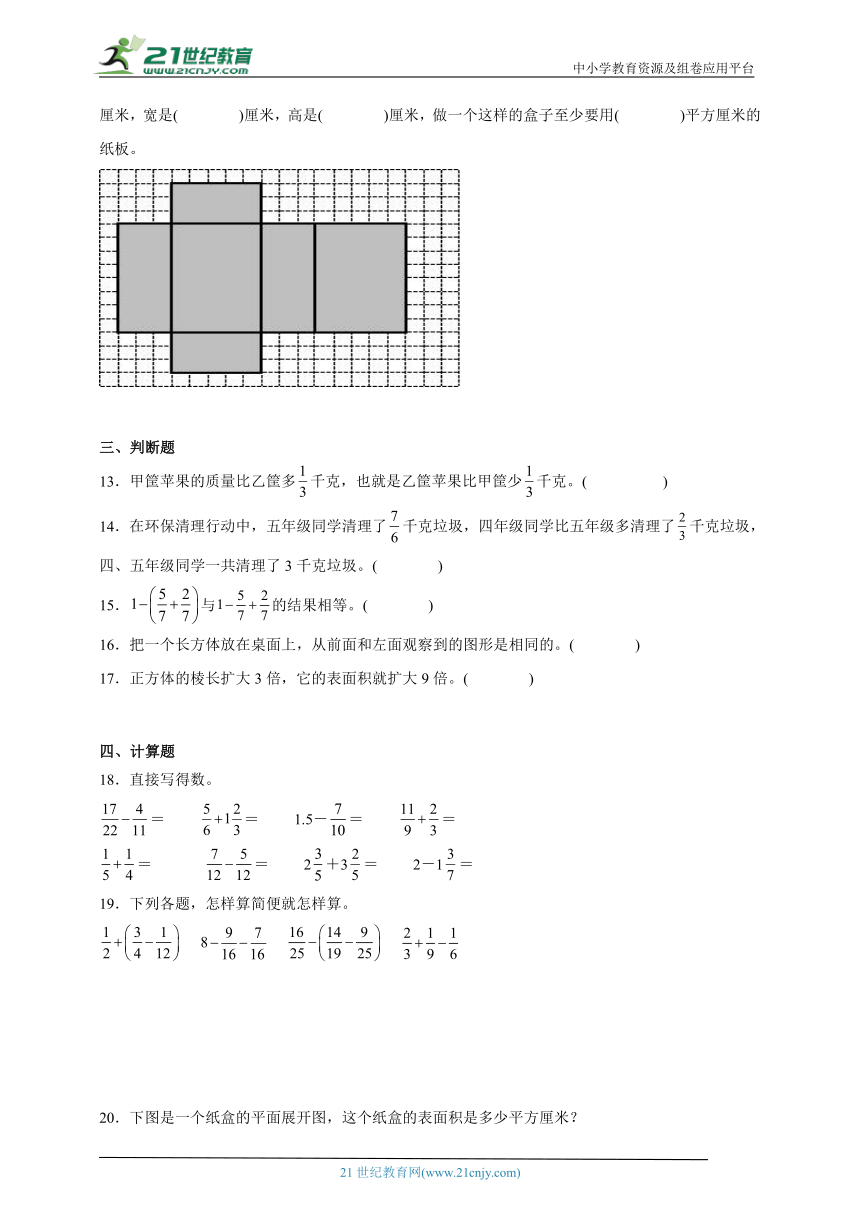
12.下图是一个长方体盒子的展开图(每个小长方形的边长是1厘米),这个盒子的长是( )厘米,宽是( )厘米,高是( )厘米,做一个这样的盒子至少要用( )平方厘米的纸板。
三、判断题
13.甲筐苹果的质量比乙筐多千克,也就是乙筐苹果比甲筐少千克。( )
14.在环保清理行动中,五年级同学清理了千克垃圾,四年级同学比五年级多清理了千克垃圾,四、五年级同学一共清理了3千克垃圾。( )
15.与的结果相等。( )
16.把一个长方体放在桌面上,从前面和左面观察到的图形是相同的。( )
17.正方体的棱长扩大3倍,它的表面积就扩大9倍。( )
四、计算题
18.直接写得数。
= = 1.5-= =
= = 2+3= 2-1=
19.下列各题,怎样算简便就怎样算。
20.下图是一个纸盒的平面展开图,这个纸盒的表面积是多少平方厘米?
五、解答题
21.今年2月,一批共享电动车投放到了乐乐的家乡。其中老城区投放共享电动车的数量占总数量的,新城区投放的数量比老城区多占总数量的,其余的投放到工业园区。工业园区投放的共享电动车的数量占总数量的几分之几?
22.同学们采集树种,第一天采集了千克,第二天比第一天多采集了千克,第二天采集了多少千克的树种?
23.有三根跳绳,第一根长为米,比第三根短米。第二根比第一根长米,第二根、第三根跳绳各有多长?
24.某健身馆计划新建一个游泳池,该游泳池长20米,宽12米,深1.5米。现在要在游泳池的四周和底面都贴上白瓷砖,需要贴白瓷砖的面积是多少平方米?
25.一种长方体铁皮通风管高80厘米,底面是一个边长为25厘米的正方形。做10节这样的通风管至少需要铁皮多少平方米?
26.奇思将3盒长为20厘米、宽为10厘米、高为6厘米的饼干包成一盒,送给朋友。怎样包装最节省包装纸?计算出最节省包装纸的面积。(接口处不计)
参考答案:
1.D
【分析】把全书的页数看作单位“1”,两天正好看完这本书的一半,即看完这本书的,用减去第一天看的全书的,即可求出第二天要看这本书的几分之几。
【详解】-=
即第二天要看这本书的,
故答案为:D
2.A
【分析】根据路程相同时,用的时间越短,跑步的速度越快,用的时间越长,跑步的速度越慢,先把分数化为小数,再比较大小,据此解答。
【详解】乙两人所跑路程都是100米,用时越短,跑得越快,
=0.25
0.25<0.3
所以<0.3,甲跑得快一些。
故答案为:A
3.C
【分析】找出四个算式中“2”和“5”计数单位相同的算式,“2”和“5”才可以直接加减;据此解答。
【详解】A.230+675,2在百位,5在个位,不可以直接相加;
B.2+,2表示2个一,的计数单位是,不可以直接相加;
C.0.26+2.573,2在十分位上,5也在十分位上,可以直接相加;
D.+,异分母分数,分子和分母不能直接相加。
故答案为:C
【点睛】本题主要考查了整数加法、分数加法、小数加法的算理,计算单位不同,不可以直接相加。
4.C
【分析】3个小正方体并排摆在空地上,两个正方体拼在一起会少2个面,所以正方体之间有4个面被挡住,有3个面贴着地面,共7个面看不见。所以露在外面的面有18-7=11(个),据此解答。
【详解】6×3-(3+4)
=18-7
=11(个)
3个小正方体并排摆在空地上,露在外面的面有11个。
故答案为:C
5.C
【分析】把长方体木料沿横截面截成三段,则表面积比原来增加4个横截面的面积,据此计算并选择即可。
【详解】2×4=8(dm2)
则表面积增加。
故答案为:C
6.C
【分析】从图中可知,在大正方体的右上角截去一个小正方体后,表面积减少了小正方体的3个面,同时又露出了3个相同的面,所以表面积没有变化。
【详解】在棱长为2cm的正方体上截去一个棱长为1cm的小正方体,表面积与原来比,不变。
故答案为:C
7.16;24;0.75
【分析】根据分数的基本性质,的分子和分母都乘4就是;根据分数与除法的关系,=3÷4;根据商不变的规律,3÷4=18÷24;把化成小数是0.75;据此解答。
【详解】==18÷24=0.75
8.2
【分析】根据分数化小数的方法,用分子除以分母即可化为小数,再根据循环小数的表示方法,在循环小数的循环节的首位和末尾数字上点上小黑点即可,即=3÷11=,观察可知,循环节是27,即一个周期,确定周期后,用2023除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数个周期多n个,也就是余数是n,那么结果为下一个周期里的第n个;如果不是从第一个开始循环,可以从总量减掉不是循环的个数后,再继续计算。
【详解】=3÷11=
2023÷2=1011(个) 1
则这个小数的小数点后第2023位的数字是2。
9.3
【分析】符合条件的所有真分数有,,,,,,计算它们的和,用加法计算,依此计算。
【详解】
=
=
=
10. 48 94
【分析】由题意可知,求铁丝的长度就是求长方体的总棱长,根据长方体的总棱长公式:L=(a+b+h)×4,据此代入数值进行计算即可;求塑料板的面积就是求长方体的表面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,据此进行计算即可。
【详解】(5+4+3)×4
=12×4
=48(厘米)
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方厘米)
则做这个框架共要48厘米的铁丝;若在它的表面贴上塑料板,共要94平方厘米塑料板。
11.18
【分析】根据正方体的特征,正方体有6个面,每个面的面积相等;把一个正方体锯成两个长方体,增加的表面积即原正方体的两个表面的总面积,表面积增加了6 cm2,所以原正方体一个面的面积为6÷2=3(cm2),由此可计算原正方体的表面积。
【详解】6÷2=3(cm2)
3×6=18(cm2)
所以把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是18cm2。
12. 8 5 3 158
【分析】看图可知,这个盒子的长、宽、高分别是8厘米、5厘米和3厘米。长方体表面积=(长×宽+长×高+宽×高)×2,将数据代入公式,求出做一个这样的盒子至少要用多少平方厘米的纸板。
【详解】(8×5+8×3+5×3)×2
=(40+24+15)×2
=79×2
=158(平方厘米)
所以,这个盒子的长是8厘米,宽是5厘米,高是3厘米,做一个这样的盒子至少要用158平方厘米的纸板。
【点睛】本题考查了长方体的展开图和表面积,熟记长方体表面积公式是解题的关键。
13.√
【分析】由题意可知乙筐的质量=甲的质量-千克,那么甲的质量=乙的质量+千克,由此判定即可。
【详解】设甲筐苹果重1千克,比乙筐多千克,则乙筐有(1-)千克;
乙筐苹果比甲筐少:
1-(1-)
=1-
=(千克)
由此可知,甲筐苹果的质量比乙筐多千克,也就是乙筐苹果比甲筐少千克,说法正确。
故答案为:√
【点睛】解决此题的关键是分清千克表示的是具体的数量,不是分率。
14.√
【分析】用五年级同学清理的垃圾千克数,加上四年级同学比五年级多清理的千克,得出四年级同学清理的垃圾千克数,再将两个年级清理的垃圾千克数相加即可。
【详解】由分析可得:
++
=++
=+
=3(千克)
四、五年级同学一共清理了3千克垃圾,所以原题判断正确。
故答案为:√
【点睛】本题考查了分数加法的计算及应用,理解题意,找对数量关系,列式解答即可。
15.×
【分析】先算括号里的加法,再算括号外的减法,然后计算,只含有加减法,按照从左向右的顺序,求出结果,然后再判断即可。
【详解】
=1-1
=0
=
=
0≠,因此与的结果相等的说法不正确。
故答案为:×
【点睛】只含有一级运算的,按照从左向右的顺序进行计算。
16.×
【分析】长方体有6个面,相对的面完全一样,前面和左面不是相对的面,从前面和左面观察到的图形可能相同也可能不同,举例说明即可。
【详解】如图,从前面看到的图形是,从左面观察到的图形是,从前面和左面观察到的图形是不相同的,所以原题说法错误。
故答案为:×
17.√
【分析】设扩大前的正方体的棱长是1,扩大后的棱长是3,根据正方体表面积公式:表面积=棱长×棱长×6,分别求出扩大前的表面积和扩大后的表面积,再用扩大后的表面积除以扩大前的表面积,即可解答。
【详解】设扩大前正方体棱长为1,则扩大后的正方体棱长为3。
(3×3×6)÷(1×1×6)
=(9×6)÷(1×6)
=54÷6
=9
正方体的棱长扩大3倍,它的表面积就扩大9倍。
原题干说法正确。
故答案为:√
【点睛】熟练掌握正方体表面积公式是解答本题的关键。
18.;;0.8;
;;6;
【详解】略。
19.;7;;
【分析】+(-),先计算括号里的减法,再计算括号外的加法;
8--,根据减法性质,原式化为:8-(+),再进行计算;
-(-),根据减法性质,原式化为:-+,然后将原式化为:+-,再进行计算;
+-,按照从左到右的运算顺序进行计算。
【详解】+(-)
=+(-)
=+
=+
=
8--
=8-(+)
=8-1
=7
-(-)
=-+
=+-
=1-
=
+-
=+-
=-
=-
=
20.1300平方厘米
【分析】观察图形可知,这个纸盒的长是20厘米,宽是15厘米,高是10厘米,求这个纸盒的表面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(20×15+20×10+15×10)×2
=(300+200+150)×2
=(500+150)×2
=650×2
=1300(平方厘米)
这个纸盒的表面积是1300平方厘米。
21.
【分析】把这批共享电动车的数量看作单位“1”,根据加法的意义,则新城区投放的数量占总数量的(+),用单位“1”减去老城区和新城区占总数量的分率即可求出工业园区投放的共享电动车的数量占总数量的几分之几。
【详解】1--(+)
=1--(+)
=1--
=-
=
答:工业园区投放的共享电动车的数量占总数量的。
22.千克
【分析】用第一天采集的数量+千克,即可求出第二天采集的数量。
【详解】+
=+
=(千克)
答:第二天采集了千克。
【点睛】本题考查异分数加法的计算,熟练掌握它的计算方法并灵活运用,同时要注意分数后面加单位表示具体的数。
23.第二根跳绳长米,第三根跳绳长米
【分析】根据加法的意义,用第一根的长度加上第一根比第三根短的长度即可求出第三根的长度;用第一根的长度加上第二根比第一根长的长度即可求出第二根的长度。
【详解】+=(米)
+=(米)
答:第二根跳绳长米,第三根跳绳长米。
24.336平方米
【分析】求需要贴瓷砖的面积,就是求这个游泳池5个面积的面积和,即求这个游泳池的底面、前后面、左右面的面积之和;根据长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】20×12+(20×1.5+12×1.5)×2
=240+(30+18)×2
=240+48×2
=240+96
=336(平方米)
答:需要贴瓷砖的面积是336平方米。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
25.8平方米
【分析】根据通分管的实际形状可知,通风管的表面积只是长方体的侧面积;不含底面,求10节这样的通风管的侧面积,需要先求出一节的侧面积;侧面的4个相等的长25厘米,宽是80厘米的长方形,根据长方形面积公式:面积=长×宽,代入数据,求出一个侧面积,再乘10,即可解答。
【详解】25×80×4×10
=2000×4×10
=8000×10
=80000(平方厘米)
80000平方厘米=8平方米
答:做10节这样的通风管的至少需要铁皮8平方米。
【点睛】解答本题的关键是明确通风管的面积就是长方体的侧面积。
26.将长为20厘米、宽为10厘米的面相互叠加包装起来最节省包装纸;面积:1480平方厘米
【分析】根据题意可知,要想最节省包装纸,把这3个长方形盒子的最大面叠加在一起,即20×10这个面叠加在一起;拼成一个长是20厘米,宽是10厘米,高是6×3=18厘米的长方体;再根据长方体的表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】将长为20厘米、宽为10厘米的面相互叠加包装起来最节省包装纸;
叠加后的长方体的长是20厘米,宽是10厘米,高是6×3=18(厘米)。
(20×10+20×18+10×18)×2
=(200+360+180)×2
=(560+180)×2
=740×2
=1480(平方厘米)
答:将长为20厘米、宽为10厘米的面相互叠加包装起来最节省包装纸;包装纸的面积是1480平方厘米。
【点睛】熟练掌握长方特表面积公式是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-2单元质量调研卷-数学五年级下册北师大版
一、选择题
1.淘气看一本书,第一天看了全书的,第二天要看这本书的( ),才能保证两天正好看完这本书的一半。
A. B. C. D.
2.甲、乙两人进行百米赛跑,甲用了分,乙用了0.3分,( )跑得快一些。
A.甲 B.乙 C.一样快 D.无法比较
3.下面各题中“2”和“5”可以直接相加的算式是( )。
A.230+675 B.2+ C.0.26+2.573 D.+
4.3个小正方体并排摆在空地上,露在外面的面有( )。
A.3个 B.9个 C.11个 D.14个
5.一块长方体木料横截面的面积是,李师傅要把它沿横截面截成三段,表面积增加( )。
A. B. C. D.
6.如图,在棱长为2cm的正方体上截去一个棱长为1cm的小正方体。表面积与原来比,( )。
A.变大了 B.变小了 C.不变 D.无法确定
二、填空题
7.(填小数)。
8.把转化为小数,这个小数的小数点后第2023位的数字是( )。
9.已知是最简真分数,那么符合条件的所有真分数的和是( )。
10.一个长方体框架,长5厘米,宽4厘米,高3厘米,做这个框架共要( )厘米的铁丝;若在它的表面贴上塑料板,共要( )平方厘米塑料板。
11.把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是( ) cm2。
12.下图是一个长方体盒子的展开图(每个小长方形的边长是1厘米),这个盒子的长是( )厘米,宽是( )厘米,高是( )厘米,做一个这样的盒子至少要用( )平方厘米的纸板。
三、判断题
13.甲筐苹果的质量比乙筐多千克,也就是乙筐苹果比甲筐少千克。( )
14.在环保清理行动中,五年级同学清理了千克垃圾,四年级同学比五年级多清理了千克垃圾,四、五年级同学一共清理了3千克垃圾。( )
15.与的结果相等。( )
16.把一个长方体放在桌面上,从前面和左面观察到的图形是相同的。( )
17.正方体的棱长扩大3倍,它的表面积就扩大9倍。( )
四、计算题
18.直接写得数。
= = 1.5-= =
= = 2+3= 2-1=
19.下列各题,怎样算简便就怎样算。
20.下图是一个纸盒的平面展开图,这个纸盒的表面积是多少平方厘米?
五、解答题
21.今年2月,一批共享电动车投放到了乐乐的家乡。其中老城区投放共享电动车的数量占总数量的,新城区投放的数量比老城区多占总数量的,其余的投放到工业园区。工业园区投放的共享电动车的数量占总数量的几分之几?
22.同学们采集树种,第一天采集了千克,第二天比第一天多采集了千克,第二天采集了多少千克的树种?
23.有三根跳绳,第一根长为米,比第三根短米。第二根比第一根长米,第二根、第三根跳绳各有多长?
24.某健身馆计划新建一个游泳池,该游泳池长20米,宽12米,深1.5米。现在要在游泳池的四周和底面都贴上白瓷砖,需要贴白瓷砖的面积是多少平方米?
25.一种长方体铁皮通风管高80厘米,底面是一个边长为25厘米的正方形。做10节这样的通风管至少需要铁皮多少平方米?
26.奇思将3盒长为20厘米、宽为10厘米、高为6厘米的饼干包成一盒,送给朋友。怎样包装最节省包装纸?计算出最节省包装纸的面积。(接口处不计)
参考答案:
1.D
【分析】把全书的页数看作单位“1”,两天正好看完这本书的一半,即看完这本书的,用减去第一天看的全书的,即可求出第二天要看这本书的几分之几。
【详解】-=
即第二天要看这本书的,
故答案为:D
2.A
【分析】根据路程相同时,用的时间越短,跑步的速度越快,用的时间越长,跑步的速度越慢,先把分数化为小数,再比较大小,据此解答。
【详解】乙两人所跑路程都是100米,用时越短,跑得越快,
=0.25
0.25<0.3
所以<0.3,甲跑得快一些。
故答案为:A
3.C
【分析】找出四个算式中“2”和“5”计数单位相同的算式,“2”和“5”才可以直接加减;据此解答。
【详解】A.230+675,2在百位,5在个位,不可以直接相加;
B.2+,2表示2个一,的计数单位是,不可以直接相加;
C.0.26+2.573,2在十分位上,5也在十分位上,可以直接相加;
D.+,异分母分数,分子和分母不能直接相加。
故答案为:C
【点睛】本题主要考查了整数加法、分数加法、小数加法的算理,计算单位不同,不可以直接相加。
4.C
【分析】3个小正方体并排摆在空地上,两个正方体拼在一起会少2个面,所以正方体之间有4个面被挡住,有3个面贴着地面,共7个面看不见。所以露在外面的面有18-7=11(个),据此解答。
【详解】6×3-(3+4)
=18-7
=11(个)
3个小正方体并排摆在空地上,露在外面的面有11个。
故答案为:C
5.C
【分析】把长方体木料沿横截面截成三段,则表面积比原来增加4个横截面的面积,据此计算并选择即可。
【详解】2×4=8(dm2)
则表面积增加。
故答案为:C
6.C
【分析】从图中可知,在大正方体的右上角截去一个小正方体后,表面积减少了小正方体的3个面,同时又露出了3个相同的面,所以表面积没有变化。
【详解】在棱长为2cm的正方体上截去一个棱长为1cm的小正方体,表面积与原来比,不变。
故答案为:C
7.16;24;0.75
【分析】根据分数的基本性质,的分子和分母都乘4就是;根据分数与除法的关系,=3÷4;根据商不变的规律,3÷4=18÷24;把化成小数是0.75;据此解答。
【详解】==18÷24=0.75
8.2
【分析】根据分数化小数的方法,用分子除以分母即可化为小数,再根据循环小数的表示方法,在循环小数的循环节的首位和末尾数字上点上小黑点即可,即=3÷11=,观察可知,循环节是27,即一个周期,确定周期后,用2023除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数个周期多n个,也就是余数是n,那么结果为下一个周期里的第n个;如果不是从第一个开始循环,可以从总量减掉不是循环的个数后,再继续计算。
【详解】=3÷11=
2023÷2=1011(个) 1
则这个小数的小数点后第2023位的数字是2。
9.3
【分析】符合条件的所有真分数有,,,,,,计算它们的和,用加法计算,依此计算。
【详解】
=
=
=
10. 48 94
【分析】由题意可知,求铁丝的长度就是求长方体的总棱长,根据长方体的总棱长公式:L=(a+b+h)×4,据此代入数值进行计算即可;求塑料板的面积就是求长方体的表面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,据此进行计算即可。
【详解】(5+4+3)×4
=12×4
=48(厘米)
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方厘米)
则做这个框架共要48厘米的铁丝;若在它的表面贴上塑料板,共要94平方厘米塑料板。
11.18
【分析】根据正方体的特征,正方体有6个面,每个面的面积相等;把一个正方体锯成两个长方体,增加的表面积即原正方体的两个表面的总面积,表面积增加了6 cm2,所以原正方体一个面的面积为6÷2=3(cm2),由此可计算原正方体的表面积。
【详解】6÷2=3(cm2)
3×6=18(cm2)
所以把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是18cm2。
12. 8 5 3 158
【分析】看图可知,这个盒子的长、宽、高分别是8厘米、5厘米和3厘米。长方体表面积=(长×宽+长×高+宽×高)×2,将数据代入公式,求出做一个这样的盒子至少要用多少平方厘米的纸板。
【详解】(8×5+8×3+5×3)×2
=(40+24+15)×2
=79×2
=158(平方厘米)
所以,这个盒子的长是8厘米,宽是5厘米,高是3厘米,做一个这样的盒子至少要用158平方厘米的纸板。
【点睛】本题考查了长方体的展开图和表面积,熟记长方体表面积公式是解题的关键。
13.√
【分析】由题意可知乙筐的质量=甲的质量-千克,那么甲的质量=乙的质量+千克,由此判定即可。
【详解】设甲筐苹果重1千克,比乙筐多千克,则乙筐有(1-)千克;
乙筐苹果比甲筐少:
1-(1-)
=1-
=(千克)
由此可知,甲筐苹果的质量比乙筐多千克,也就是乙筐苹果比甲筐少千克,说法正确。
故答案为:√
【点睛】解决此题的关键是分清千克表示的是具体的数量,不是分率。
14.√
【分析】用五年级同学清理的垃圾千克数,加上四年级同学比五年级多清理的千克,得出四年级同学清理的垃圾千克数,再将两个年级清理的垃圾千克数相加即可。
【详解】由分析可得:
++
=++
=+
=3(千克)
四、五年级同学一共清理了3千克垃圾,所以原题判断正确。
故答案为:√
【点睛】本题考查了分数加法的计算及应用,理解题意,找对数量关系,列式解答即可。
15.×
【分析】先算括号里的加法,再算括号外的减法,然后计算,只含有加减法,按照从左向右的顺序,求出结果,然后再判断即可。
【详解】
=1-1
=0
=
=
0≠,因此与的结果相等的说法不正确。
故答案为:×
【点睛】只含有一级运算的,按照从左向右的顺序进行计算。
16.×
【分析】长方体有6个面,相对的面完全一样,前面和左面不是相对的面,从前面和左面观察到的图形可能相同也可能不同,举例说明即可。
【详解】如图,从前面看到的图形是,从左面观察到的图形是,从前面和左面观察到的图形是不相同的,所以原题说法错误。
故答案为:×
17.√
【分析】设扩大前的正方体的棱长是1,扩大后的棱长是3,根据正方体表面积公式:表面积=棱长×棱长×6,分别求出扩大前的表面积和扩大后的表面积,再用扩大后的表面积除以扩大前的表面积,即可解答。
【详解】设扩大前正方体棱长为1,则扩大后的正方体棱长为3。
(3×3×6)÷(1×1×6)
=(9×6)÷(1×6)
=54÷6
=9
正方体的棱长扩大3倍,它的表面积就扩大9倍。
原题干说法正确。
故答案为:√
【点睛】熟练掌握正方体表面积公式是解答本题的关键。
18.;;0.8;
;;6;
【详解】略。
19.;7;;
【分析】+(-),先计算括号里的减法,再计算括号外的加法;
8--,根据减法性质,原式化为:8-(+),再进行计算;
-(-),根据减法性质,原式化为:-+,然后将原式化为:+-,再进行计算;
+-,按照从左到右的运算顺序进行计算。
【详解】+(-)
=+(-)
=+
=+
=
8--
=8-(+)
=8-1
=7
-(-)
=-+
=+-
=1-
=
+-
=+-
=-
=-
=
20.1300平方厘米
【分析】观察图形可知,这个纸盒的长是20厘米,宽是15厘米,高是10厘米,求这个纸盒的表面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(20×15+20×10+15×10)×2
=(300+200+150)×2
=(500+150)×2
=650×2
=1300(平方厘米)
这个纸盒的表面积是1300平方厘米。
21.
【分析】把这批共享电动车的数量看作单位“1”,根据加法的意义,则新城区投放的数量占总数量的(+),用单位“1”减去老城区和新城区占总数量的分率即可求出工业园区投放的共享电动车的数量占总数量的几分之几。
【详解】1--(+)
=1--(+)
=1--
=-
=
答:工业园区投放的共享电动车的数量占总数量的。
22.千克
【分析】用第一天采集的数量+千克,即可求出第二天采集的数量。
【详解】+
=+
=(千克)
答:第二天采集了千克。
【点睛】本题考查异分数加法的计算,熟练掌握它的计算方法并灵活运用,同时要注意分数后面加单位表示具体的数。
23.第二根跳绳长米,第三根跳绳长米
【分析】根据加法的意义,用第一根的长度加上第一根比第三根短的长度即可求出第三根的长度;用第一根的长度加上第二根比第一根长的长度即可求出第二根的长度。
【详解】+=(米)
+=(米)
答:第二根跳绳长米,第三根跳绳长米。
24.336平方米
【分析】求需要贴瓷砖的面积,就是求这个游泳池5个面积的面积和,即求这个游泳池的底面、前后面、左右面的面积之和;根据长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】20×12+(20×1.5+12×1.5)×2
=240+(30+18)×2
=240+48×2
=240+96
=336(平方米)
答:需要贴瓷砖的面积是336平方米。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
25.8平方米
【分析】根据通分管的实际形状可知,通风管的表面积只是长方体的侧面积;不含底面,求10节这样的通风管的侧面积,需要先求出一节的侧面积;侧面的4个相等的长25厘米,宽是80厘米的长方形,根据长方形面积公式:面积=长×宽,代入数据,求出一个侧面积,再乘10,即可解答。
【详解】25×80×4×10
=2000×4×10
=8000×10
=80000(平方厘米)
80000平方厘米=8平方米
答:做10节这样的通风管的至少需要铁皮8平方米。
【点睛】解答本题的关键是明确通风管的面积就是长方体的侧面积。
26.将长为20厘米、宽为10厘米的面相互叠加包装起来最节省包装纸;面积:1480平方厘米
【分析】根据题意可知,要想最节省包装纸,把这3个长方形盒子的最大面叠加在一起,即20×10这个面叠加在一起;拼成一个长是20厘米,宽是10厘米,高是6×3=18厘米的长方体;再根据长方体的表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】将长为20厘米、宽为10厘米的面相互叠加包装起来最节省包装纸;
叠加后的长方体的长是20厘米,宽是10厘米,高是6×3=18(厘米)。
(20×10+20×18+10×18)×2
=(200+360+180)×2
=(560+180)×2
=740×2
=1480(平方厘米)
答:将长为20厘米、宽为10厘米的面相互叠加包装起来最节省包装纸;包装纸的面积是1480平方厘米。
【点睛】熟练掌握长方特表面积公式是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
