2023-2024学年数学九年级下册人教版第二十六章反比例函数经典题型检测卷(含答案)
文档属性
| 名称 | 2023-2024学年数学九年级下册人教版第二十六章反比例函数经典题型检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 535.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 19:10:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册人教版第二十六章反比例函数经典题型检测卷
一、选择题
1.下列说法正确的是
A.对角线垂直的平行四边形是矩形
B.方程有两个相等的实数根
C.抛物线的顶点为
D.函数,随的增大而增大
2.已知是反比例函数上一点,下列各点不在上的是
A. B.
C. D.(,8)
3.已知反比例函数,当时,y随x增大而增大,则a的值可能是( )
A.1 B.2 C.3 D.4
4.已知ab<0, 一次函数y=ax-b与反比例函数y=在同一直角坐标系中的图象可能是( )
A. B.
C. D.
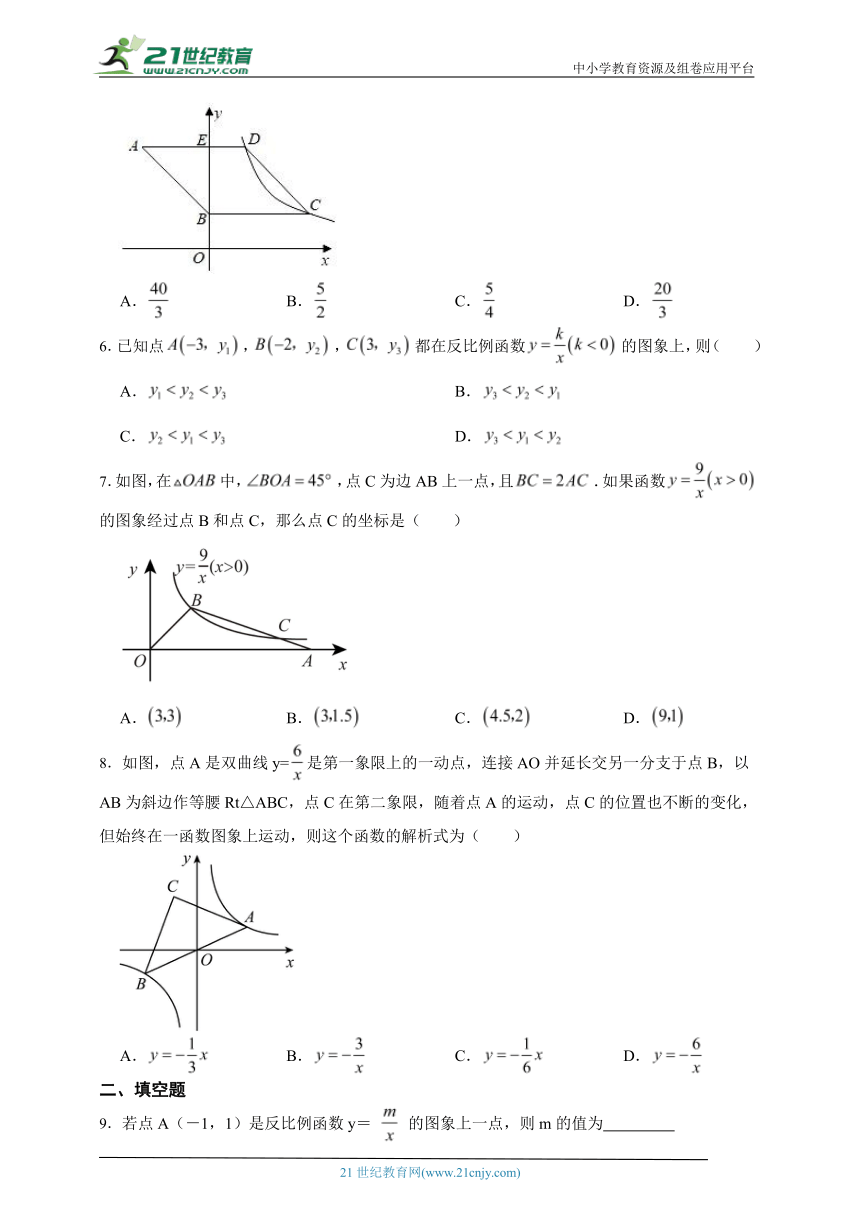
5.如图,在平面直角坐标系中,菱形ABCD的边AD⊥y轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数y=(k≠0,x>0)的图象同时经过顶点C、D.若点C的横坐标为5,BE=2DE,则k的值为( )
A. B. C. D.
6.已知点,,都在反比例函数的图象上,则( )
A. B.
C. D.
7.如图,在中,,点C为边AB上一点,且.如果函数的图象经过点B和点C,那么点C的坐标是( )
A. B. C. D.
8.如图,点A是双曲线y=是第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A. B. C. D.
二、填空题
9.若点A(-1,1)是反比例函数y= 的图象上一点,则m的值为
10.如图,已知点P(1,2)在反比例函数 的图象上,观察图象可知,当x>1时,y的取值范围是 .
11.设函数 与 的图象的交点坐标为 ,则 的值为 .
12.已知点 为反比例函数图象上不同的两点,A坐标为 ,过点A作 轴于点C,过点B作 轴于点D,连结 ,若 ,则点B坐标为 .
13.如图,已知,点A在反比例函数图象上,点B在x轴正半轴上,,,直线与反比例函数的图象只有一个公共点,则 .
14.如图,点A为双曲线在第二象限上的动点,AO的延长线与双曲线的另一个交点为B,以AB为边的矩形ABCD满足AB:BC=3:2,对角线AC,BD交于点P,设P的坐标为(m,n),则m、n满足的关系式为 .
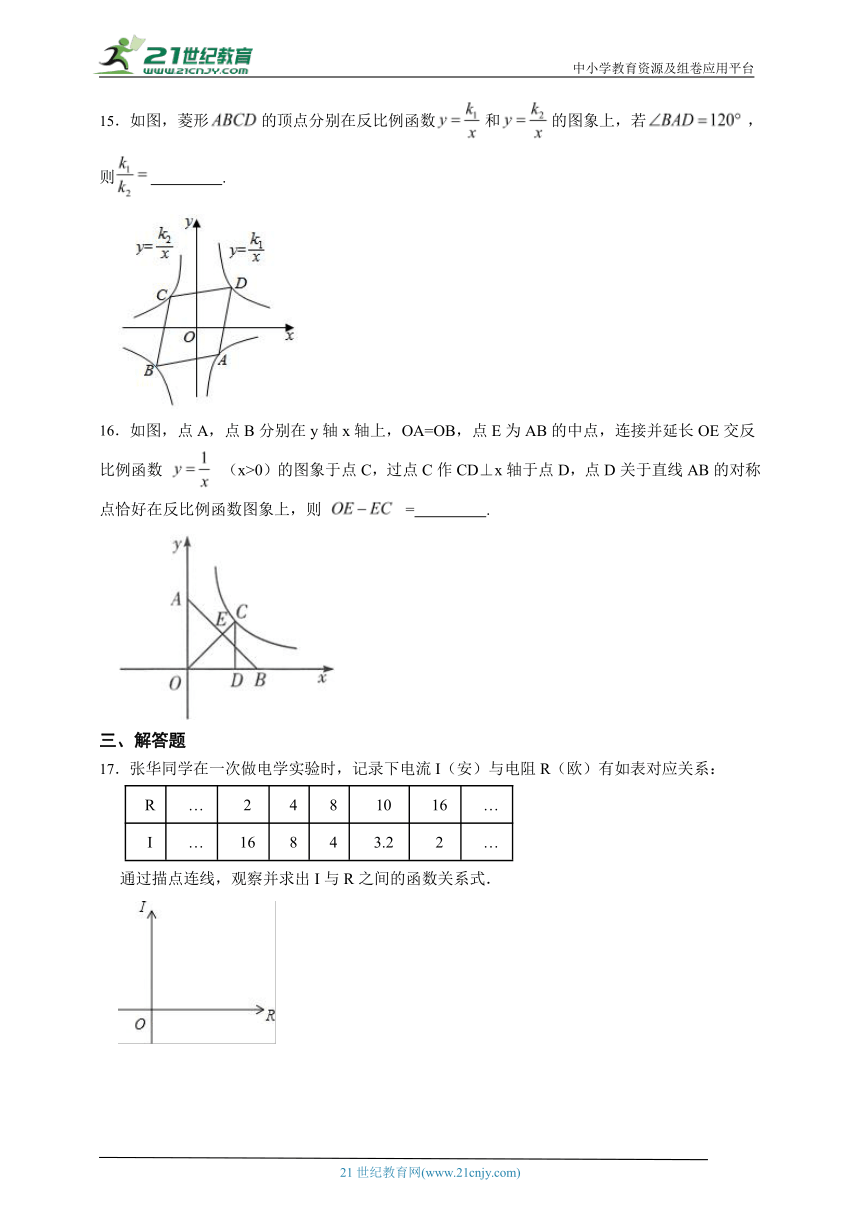
15.如图,菱形的顶点分别在反比例函数和的图象上,若,则 .
16.如图,点A,点B分别在y轴x轴上,OA=OB,点E为AB的中点,连接并延长OE交反比例函数 (x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则 = .
三、解答题
17.张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
R … 2 4 8 10 16 …
I … 16 8 4 3.2 2 …
通过描点连线,观察并求出I与R之间的函数关系式.
18.已知(且).
(1)化简A;
(2)若点在反比例函数的图象上,求A的值.
19.如图,直线与双曲线(k为常数,交于,两点,与轴、轴分别交于,两点,点的坐标为.
(1)求反比例函数的解析式.
(2)结合图象直接写出当时,的取值范围.
20.已知点P(m,4)在反比例函数y=的图象上,正比例函数的图象经过点P和点Q(4,n).
(1)求点P的坐标;
(2)求正比例函数的表达式和点Q的坐标;
(3)在x轴上求一点M,使△MPQ的面积等于18.
21.如图,一次函数图象与反比例函数图象交于点A(-1,6),B(,a-3),与x轴交于点C,与y轴交于点D.
(1)求反比例函数与一次函数的表达式;
(2)点M在x轴上,若S△OAM=S△OAB,求点M的坐标.
22.如图,直线y=ax+b(a≠0)与反比例函数的图象相交于点A(2,3),B(6,m).
(1)求k和m的值.
(2)根据图象直接写出当x>0且时,自变量x的取值范围.
(3)请问在x轴上是否存在点C,使得△ABC是等腰直角三角形 若存在,请直接写出点C的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】-1
10.【答案】0<y<2
11.【答案】 或
12.【答案】( ),(4,1),(2,2)
13.【答案】12
14.【答案】
15.【答案】-3
16.【答案】
17.【答案】解:如图,
由图可知I与R之间满足反比例函数关系,设I= ,
将(2,16)代入得:k=32,
故I=
18.【答案】(1)解:.
(2)解:∵点在反比例函数的图象上,
∴,
∴.
19.【答案】(1)解:把代入直线,可得,
解得,
,
把代入双曲线为常数,(k≠0),可得,
双曲线的解析式为;
(2)解:
得或,
,
由图象可知,当时,的取值范围或.
20.【答案】(1)解: ∵点P(m,4)在反比例函数y= 的图象上,∴4m=-8,
∴m=-2,∴点P的坐标为(-2,4).
(2)解:设正比例函数表达式为y=kx(k≠0),∵正比例函数图象经过点P,∴-2k=4,∴k=-2,∴正比例函数的表达式为y=-2x,∵正比.例函数图象经过点Q(4,n),∴n=-8,∴点Q的坐标为(4,-8).
(3)解:S△MPQ = S△QOM+S△POM,∴S△MPO = ×80M+ ×40M =60M.∵△MPQ的面积等于18,∴60M=18,解得OM=3.∵点M在x轴上,∴点M在原点左边时,点M的坐标为(-3,0),点M在原点右边时,点M的坐标为(3,0).综上所述,点M的坐标为(-3,0)或(3,0).
21.【答案】(1)解:由题意,设反比例函数、一次函数的表达式分别为y= (n≠0) ,y=kx+b(h≠0),
∵点A(-1,6)在反比例函数图象上,
∴n=-6,
∴反比例函数的表达式为y=
∵点B在反比例函数图象上,
∴(a-3)=-6,
∴a= 1,
∴点B的坐标为(3,-2).
∵点A(-1,6) ,B(3,-2)在一次函数y=kx+b(k≠0)的图象上,
∴
∴
∴一次函数的表达式为y=-2x+4.
(2)解:设点M(m,0),由(1)得直线y=-2x+4交x轴于点C(2,0),
∴OC=2,
∴S△AOB=S△AOC+S△COB= OC×6+ OC×2=6+2= 8.
∵M在x轴上,
∴S△AOM= OM×6=3lmI,
又S△AOB=S△AOM,
∴3|m|=8,
∴m=±
∴点M的坐标为(,0)或(-,0),
22.【答案】(1)解:∵点A,B在反比例函数图象上,
∴k=2×3=6m
解之:k=6,m=1.
(2)解:2(3)解:存在,
设点C(x,0),
∵点A(2,3),点B(6,1),
∴AB2=(6-2)2+(3-1)2=20,
AC2=(x-2)2+9=x2-4x+13,BC2=(x-6)2+1=x2-12x+37
当∠ABC=90°时,则AB2+BC2=AC2即20+x2-12x+37=
x2-4x+13
解之:x=,
∴BC2=(-6)2+1=≠20,
∴BC≠AB,故不符合题意;
当∠ACB=90°时,则AC2+BC2=AB2即x2-4x+13+x2-12x+37=20
解之:x=3或x=5,
当x=5时,AC2=(5-2)2+9=18,BC2=(5-6)2+1=2
∴AC≠BC,故不符合题意;
当x=3时AC2=(3-2)2+9=10,BC2=(3-6)2+1=10,
∴AC=BC,故符合题意;
∴点C(3,0)
当∠BAC=90°时则AC2+BA2=CB2即x2-4x+13+20=x2-12x+37,
解之:x=,
∴AC2=(-2)2+9=≠20,
∴AC≠AB,故不符合题意;
综上所述,存在满足条件的点C,其坐标为(3,0)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学九年级下册人教版第二十六章反比例函数经典题型检测卷
一、选择题
1.下列说法正确的是
A.对角线垂直的平行四边形是矩形
B.方程有两个相等的实数根
C.抛物线的顶点为
D.函数,随的增大而增大
2.已知是反比例函数上一点,下列各点不在上的是
A. B.
C. D.(,8)
3.已知反比例函数,当时,y随x增大而增大,则a的值可能是( )
A.1 B.2 C.3 D.4
4.已知ab<0, 一次函数y=ax-b与反比例函数y=在同一直角坐标系中的图象可能是( )
A. B.
C. D.
5.如图,在平面直角坐标系中,菱形ABCD的边AD⊥y轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数y=(k≠0,x>0)的图象同时经过顶点C、D.若点C的横坐标为5,BE=2DE,则k的值为( )
A. B. C. D.
6.已知点,,都在反比例函数的图象上,则( )
A. B.
C. D.
7.如图,在中,,点C为边AB上一点,且.如果函数的图象经过点B和点C,那么点C的坐标是( )
A. B. C. D.
8.如图,点A是双曲线y=是第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A. B. C. D.
二、填空题
9.若点A(-1,1)是反比例函数y= 的图象上一点,则m的值为
10.如图,已知点P(1,2)在反比例函数 的图象上,观察图象可知,当x>1时,y的取值范围是 .
11.设函数 与 的图象的交点坐标为 ,则 的值为 .
12.已知点 为反比例函数图象上不同的两点,A坐标为 ,过点A作 轴于点C,过点B作 轴于点D,连结 ,若 ,则点B坐标为 .
13.如图,已知,点A在反比例函数图象上,点B在x轴正半轴上,,,直线与反比例函数的图象只有一个公共点,则 .
14.如图,点A为双曲线在第二象限上的动点,AO的延长线与双曲线的另一个交点为B,以AB为边的矩形ABCD满足AB:BC=3:2,对角线AC,BD交于点P,设P的坐标为(m,n),则m、n满足的关系式为 .
15.如图,菱形的顶点分别在反比例函数和的图象上,若,则 .
16.如图,点A,点B分别在y轴x轴上,OA=OB,点E为AB的中点,连接并延长OE交反比例函数 (x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则 = .
三、解答题
17.张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
R … 2 4 8 10 16 …
I … 16 8 4 3.2 2 …
通过描点连线,观察并求出I与R之间的函数关系式.
18.已知(且).
(1)化简A;
(2)若点在反比例函数的图象上,求A的值.
19.如图,直线与双曲线(k为常数,交于,两点,与轴、轴分别交于,两点,点的坐标为.
(1)求反比例函数的解析式.
(2)结合图象直接写出当时,的取值范围.
20.已知点P(m,4)在反比例函数y=的图象上,正比例函数的图象经过点P和点Q(4,n).
(1)求点P的坐标;
(2)求正比例函数的表达式和点Q的坐标;
(3)在x轴上求一点M,使△MPQ的面积等于18.
21.如图,一次函数图象与反比例函数图象交于点A(-1,6),B(,a-3),与x轴交于点C,与y轴交于点D.
(1)求反比例函数与一次函数的表达式;
(2)点M在x轴上,若S△OAM=S△OAB,求点M的坐标.
22.如图,直线y=ax+b(a≠0)与反比例函数的图象相交于点A(2,3),B(6,m).
(1)求k和m的值.
(2)根据图象直接写出当x>0且时,自变量x的取值范围.
(3)请问在x轴上是否存在点C,使得△ABC是等腰直角三角形 若存在,请直接写出点C的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】-1
10.【答案】0<y<2
11.【答案】 或
12.【答案】( ),(4,1),(2,2)
13.【答案】12
14.【答案】
15.【答案】-3
16.【答案】
17.【答案】解:如图,
由图可知I与R之间满足反比例函数关系,设I= ,
将(2,16)代入得:k=32,
故I=
18.【答案】(1)解:.
(2)解:∵点在反比例函数的图象上,
∴,
∴.
19.【答案】(1)解:把代入直线,可得,
解得,
,
把代入双曲线为常数,(k≠0),可得,
双曲线的解析式为;
(2)解:
得或,
,
由图象可知,当时,的取值范围或.
20.【答案】(1)解: ∵点P(m,4)在反比例函数y= 的图象上,∴4m=-8,
∴m=-2,∴点P的坐标为(-2,4).
(2)解:设正比例函数表达式为y=kx(k≠0),∵正比例函数图象经过点P,∴-2k=4,∴k=-2,∴正比例函数的表达式为y=-2x,∵正比.例函数图象经过点Q(4,n),∴n=-8,∴点Q的坐标为(4,-8).
(3)解:S△MPQ = S△QOM+S△POM,∴S△MPO = ×80M+ ×40M =60M.∵△MPQ的面积等于18,∴60M=18,解得OM=3.∵点M在x轴上,∴点M在原点左边时,点M的坐标为(-3,0),点M在原点右边时,点M的坐标为(3,0).综上所述,点M的坐标为(-3,0)或(3,0).
21.【答案】(1)解:由题意,设反比例函数、一次函数的表达式分别为y= (n≠0) ,y=kx+b(h≠0),
∵点A(-1,6)在反比例函数图象上,
∴n=-6,
∴反比例函数的表达式为y=
∵点B在反比例函数图象上,
∴(a-3)=-6,
∴a= 1,
∴点B的坐标为(3,-2).
∵点A(-1,6) ,B(3,-2)在一次函数y=kx+b(k≠0)的图象上,
∴
∴
∴一次函数的表达式为y=-2x+4.
(2)解:设点M(m,0),由(1)得直线y=-2x+4交x轴于点C(2,0),
∴OC=2,
∴S△AOB=S△AOC+S△COB= OC×6+ OC×2=6+2= 8.
∵M在x轴上,
∴S△AOM= OM×6=3lmI,
又S△AOB=S△AOM,
∴3|m|=8,
∴m=±
∴点M的坐标为(,0)或(-,0),
22.【答案】(1)解:∵点A,B在反比例函数图象上,
∴k=2×3=6m
解之:k=6,m=1.
(2)解:2
设点C(x,0),
∵点A(2,3),点B(6,1),
∴AB2=(6-2)2+(3-1)2=20,
AC2=(x-2)2+9=x2-4x+13,BC2=(x-6)2+1=x2-12x+37
当∠ABC=90°时,则AB2+BC2=AC2即20+x2-12x+37=
x2-4x+13
解之:x=,
∴BC2=(-6)2+1=≠20,
∴BC≠AB,故不符合题意;
当∠ACB=90°时,则AC2+BC2=AB2即x2-4x+13+x2-12x+37=20
解之:x=3或x=5,
当x=5时,AC2=(5-2)2+9=18,BC2=(5-6)2+1=2
∴AC≠BC,故不符合题意;
当x=3时AC2=(3-2)2+9=10,BC2=(3-6)2+1=10,
∴AC=BC,故符合题意;
∴点C(3,0)
当∠BAC=90°时则AC2+BA2=CB2即x2-4x+13+20=x2-12x+37,
解之:x=,
∴AC2=(-2)2+9=≠20,
∴AC≠AB,故不符合题意;
综上所述,存在满足条件的点C,其坐标为(3,0)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
