2023-2024学年高中数学苏教版必修第二册第11章解三角形检测卷(含答案)
文档属性
| 名称 | 2023-2024学年高中数学苏教版必修第二册第11章解三角形检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 624.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 17:30:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年高中数学苏教版必修第二册第11章解三角形检测卷
一、选择题
1.在中,角,,的对边分别为,,,若,,,则
A. B. C. D.
2.根据气象部门提醒,在距离某基地正北方向处的热带风暴中心正以的速度沿南偏东方向移动,距离风暴中心以内的地区都将受到影响,则该基地受热带风暴中心影响的时长为( )
A. B.
C. D.
3.数学家欧拉在1765年发现了九点圆,即在任意的三角形中,三边的中点、三条高的垂足、三条高的交点(垂心)与三角形顶点连线的中点,这九个点共圆,因此九点圆也称作欧拉圆.已知在中,,,,则的九点圆的半径为( )
A. B. C. D.
4.在中,角所对的边分别是,且为的等差中项,则角最大值是( )
A. B. C. D.
5. 在中,内角A,B,C的对边分别为a,b,c,若,,则的外接圆的面积为( )
A. B. C. D.
6.在△ABC中,∠A=30°,AB=4,满足此条件的△ABC有两解,则BC边长度的取值范围为( )
A.(2,4) B.(2,4)
C.(4,+∞) D.(2,4)
7.在中,若三边之比,则等于( )
A. B. C.2 D.-2
8.如图,、两点在河的同侧,且、两点均不可到达.现需测、两点间的距离,测量者在河对岸选定两点、,测得,同时在、两点分别测得,,,则、两点间的距离为( )
A. B. C. D.
二、多项选择题
9.设的内角的对边分别为,则下列结论正确的是( )
A.若,则
B.若,则外接圆的半径为
C.若,则
D.若,则为锐角三角形
10.已知的内角所对的边分别为,下列四个命题中正确的是( )
A.若,则一定是等腰三角形
B.若,则是等腰三角形
C.若,则一定是等边三角形
D.若,则是直角三角形
11. 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”,即以小斜幂,并大斜幕,减中斜幂,余半之,自乘于上:以小斜幂乘大斜幂,减上,余四约之,为实:一为从隅,开平方得积可用公式(其中a、b、c、S为三角形的三边和面积)表示.在中,a、b、c分别为角A、B、C所对的边,若,且,则下列命题正确的是( )
A.面积的最大值是 B.
C. D.面积的最大值是
三、填空题
12.在中,.则 ;若,则 .
13.在 中,角 所对的边分别为 ,若 , , ,则 .
14.在海岸处,发现北偏东45°方向,距处海里的处有一艘走私船,在处北偏西75°方向,距处2海里的处的缉私船奉命以海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从处向北偏东30°的方向逃窜,缉私船要最快追上走私船,所需的时间约是 分钟.(注:)
四、解答题
15.已知中,角所对的边分别为,,,,且.
(1)求角的大小;
(2)若,点在边上,且平分,求的长度.
16.在中,角的对边分别是,且.
(1)求;
(2)若的角平分线交于点,且,求的周长.
17.记的内角的对边分别是,已知,.
(1)求角的大小;
(2)求的面积.
18.在中,内角,,的对边分别为,,,且向量,,.
(1)求角的大小;
(2)若,的周长为,面积为,求的最大值.
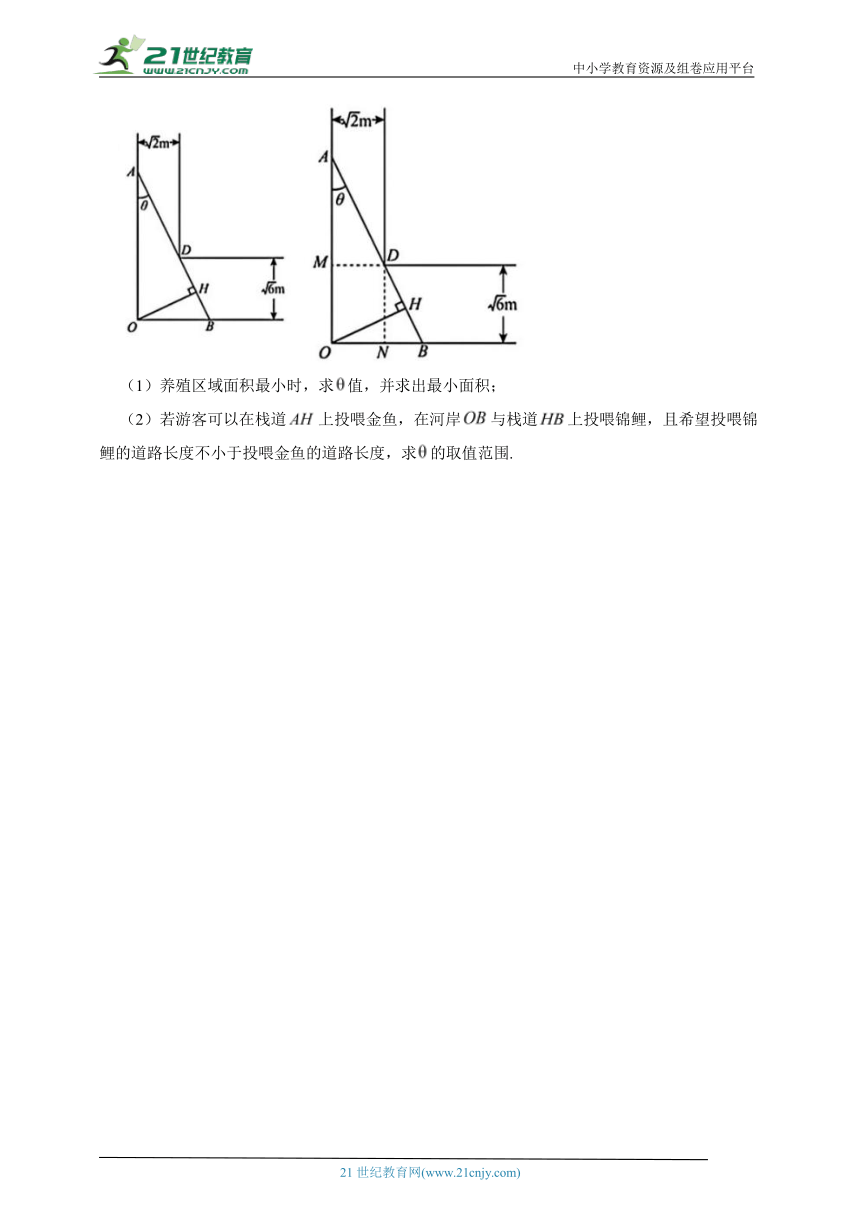
19.如图所示,有一条“”形河道,其中上方河道宽,右侧河道宽,河道均足够长.现过点修建一条栈道,开辟出直角三角形区域(图中)养殖观赏鱼,且.点在线段上,且.线段将养殖区域分为两部分,其中上方养殖金鱼,下方养殖锦鲤.
(1)养殖区域面积最小时,求值,并求出最小面积;
(2)若游客可以在栈道上投喂金鱼,在河岸与栈道上投喂锦鲤,且希望投喂锦鲤的道路长度不小于投喂金鱼的道路长度,求的取值范围.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A,C
10.【答案】B,C
11.【答案】A,B
12.【答案】;
13.【答案】
14.【答案】15
15.【答案】(1)解:因为,由正弦定理可得:,
因为,所以,即,
由余弦定理可得,
在中,,
所以.
(2)解:由(1)问可知,,
所以,解得,
设,由平分,所以,
即,
解得:,
故的长度为.
16.【答案】(1)在中,,
由正弦定理可化简得
所以可化简得
又在中,,得
,即
由,得
(2)由(1)得,又的角平分线交于点,且可得
即
即①
又在中,得
②
联立①②解得
所以的周长为
17.【答案】(1)解:
由正弦定理可得:,
,
由余弦定理:
化简得:
所以.
(2)解:由正弦定理:,
所以
则.
18.【答案】(1)解:,故,
即,故,
整理得到,即,,故.
(2)解:由余弦定理,得,即,
所以,即,
因为,,所以,
又(当且仅当时取等号),所以(当且仅当时取等号),所以(当且仅当时取等号),
所以(当且仅当时取等号),
即的最大值为(当且仅当时取等号).
19.【答案】(1)解:过作,垂直于,,垂足分别为,,则,,,,养殖观赏鱼的面积,
由可得,则,当且仅当即时取等号,故时,最小.
(2)解:由,可得,
则,,,由题意,
则,
则,则.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年高中数学苏教版必修第二册第11章解三角形检测卷
一、选择题
1.在中,角,,的对边分别为,,,若,,,则
A. B. C. D.
2.根据气象部门提醒,在距离某基地正北方向处的热带风暴中心正以的速度沿南偏东方向移动,距离风暴中心以内的地区都将受到影响,则该基地受热带风暴中心影响的时长为( )
A. B.
C. D.
3.数学家欧拉在1765年发现了九点圆,即在任意的三角形中,三边的中点、三条高的垂足、三条高的交点(垂心)与三角形顶点连线的中点,这九个点共圆,因此九点圆也称作欧拉圆.已知在中,,,,则的九点圆的半径为( )
A. B. C. D.
4.在中,角所对的边分别是,且为的等差中项,则角最大值是( )
A. B. C. D.
5. 在中,内角A,B,C的对边分别为a,b,c,若,,则的外接圆的面积为( )
A. B. C. D.
6.在△ABC中,∠A=30°,AB=4,满足此条件的△ABC有两解,则BC边长度的取值范围为( )
A.(2,4) B.(2,4)
C.(4,+∞) D.(2,4)
7.在中,若三边之比,则等于( )
A. B. C.2 D.-2
8.如图,、两点在河的同侧,且、两点均不可到达.现需测、两点间的距离,测量者在河对岸选定两点、,测得,同时在、两点分别测得,,,则、两点间的距离为( )
A. B. C. D.
二、多项选择题
9.设的内角的对边分别为,则下列结论正确的是( )
A.若,则
B.若,则外接圆的半径为
C.若,则
D.若,则为锐角三角形
10.已知的内角所对的边分别为,下列四个命题中正确的是( )
A.若,则一定是等腰三角形
B.若,则是等腰三角形
C.若,则一定是等边三角形
D.若,则是直角三角形
11. 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”,即以小斜幂,并大斜幕,减中斜幂,余半之,自乘于上:以小斜幂乘大斜幂,减上,余四约之,为实:一为从隅,开平方得积可用公式(其中a、b、c、S为三角形的三边和面积)表示.在中,a、b、c分别为角A、B、C所对的边,若,且,则下列命题正确的是( )
A.面积的最大值是 B.
C. D.面积的最大值是
三、填空题
12.在中,.则 ;若,则 .
13.在 中,角 所对的边分别为 ,若 , , ,则 .
14.在海岸处,发现北偏东45°方向,距处海里的处有一艘走私船,在处北偏西75°方向,距处2海里的处的缉私船奉命以海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从处向北偏东30°的方向逃窜,缉私船要最快追上走私船,所需的时间约是 分钟.(注:)
四、解答题
15.已知中,角所对的边分别为,,,,且.
(1)求角的大小;
(2)若,点在边上,且平分,求的长度.
16.在中,角的对边分别是,且.
(1)求;
(2)若的角平分线交于点,且,求的周长.
17.记的内角的对边分别是,已知,.
(1)求角的大小;
(2)求的面积.
18.在中,内角,,的对边分别为,,,且向量,,.
(1)求角的大小;
(2)若,的周长为,面积为,求的最大值.
19.如图所示,有一条“”形河道,其中上方河道宽,右侧河道宽,河道均足够长.现过点修建一条栈道,开辟出直角三角形区域(图中)养殖观赏鱼,且.点在线段上,且.线段将养殖区域分为两部分,其中上方养殖金鱼,下方养殖锦鲤.
(1)养殖区域面积最小时,求值,并求出最小面积;
(2)若游客可以在栈道上投喂金鱼,在河岸与栈道上投喂锦鲤,且希望投喂锦鲤的道路长度不小于投喂金鱼的道路长度,求的取值范围.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A,C
10.【答案】B,C
11.【答案】A,B
12.【答案】;
13.【答案】
14.【答案】15
15.【答案】(1)解:因为,由正弦定理可得:,
因为,所以,即,
由余弦定理可得,
在中,,
所以.
(2)解:由(1)问可知,,
所以,解得,
设,由平分,所以,
即,
解得:,
故的长度为.
16.【答案】(1)在中,,
由正弦定理可化简得
所以可化简得
又在中,,得
,即
由,得
(2)由(1)得,又的角平分线交于点,且可得
即
即①
又在中,得
②
联立①②解得
所以的周长为
17.【答案】(1)解:
由正弦定理可得:,
,
由余弦定理:
化简得:
所以.
(2)解:由正弦定理:,
所以
则.
18.【答案】(1)解:,故,
即,故,
整理得到,即,,故.
(2)解:由余弦定理,得,即,
所以,即,
因为,,所以,
又(当且仅当时取等号),所以(当且仅当时取等号),所以(当且仅当时取等号),
所以(当且仅当时取等号),
即的最大值为(当且仅当时取等号).
19.【答案】(1)解:过作,垂直于,,垂足分别为,,则,,,,养殖观赏鱼的面积,
由可得,则,当且仅当即时取等号,故时,最小.
(2)解:由,可得,
则,,,由题意,
则,
则,则.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
