【多媒体导学案】人教版数学八年级上册第12章第1课时全等三角形(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第1课时全等三角形(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 242.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览


文档简介
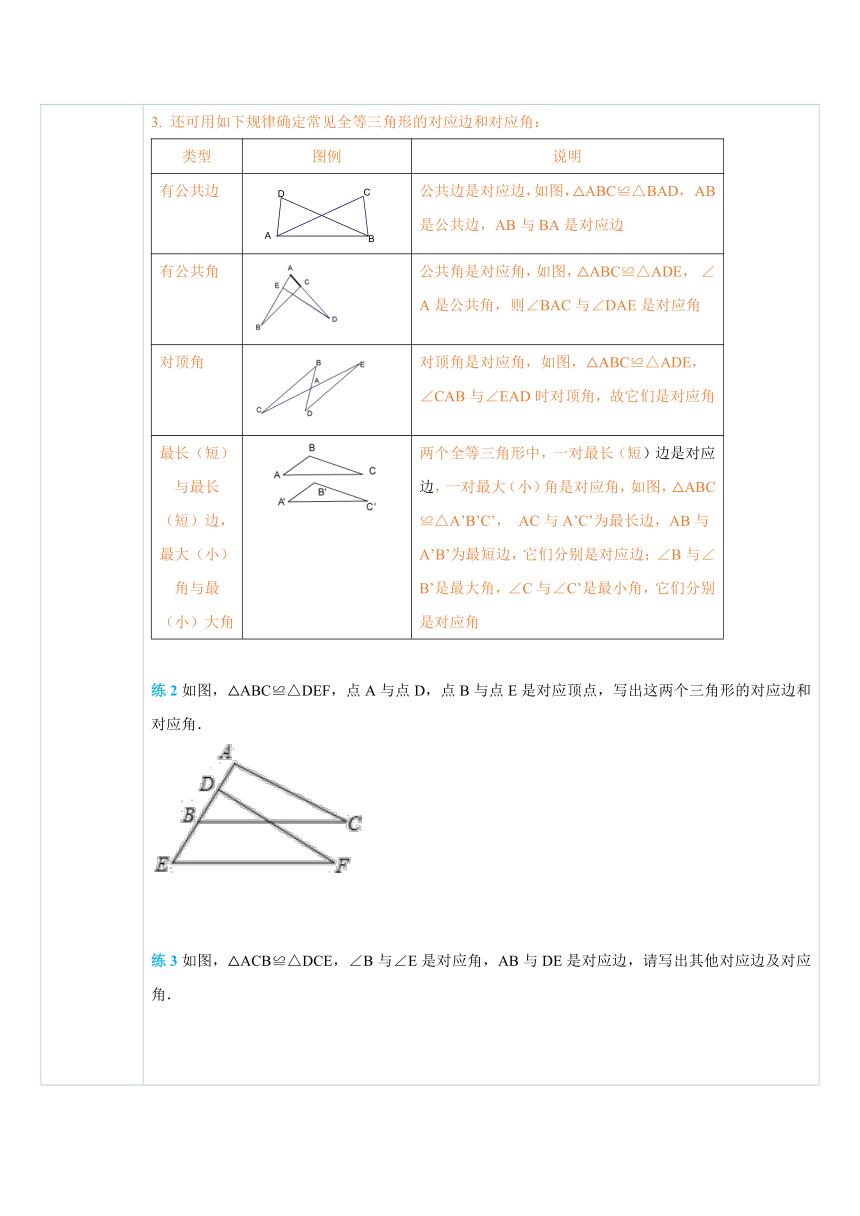
一、学习目标 1.掌握全等形、全等三角形及相关概念;2.理解“平移、翻转、旋转”前后的图形全等;3.掌握全等三角形的性质;4.熟练确定全等三角形的对应元素.
二、知识回顾 1.观察图案,指出这些图案中形状与大小相同的图形. ( http: / / www.21cnjy.com )2.请你举出生活中形状、大小完全相同的例子.
三、新知讲解 1.全等三角形的相关概念能够完全重合的两个图形叫做 全等形 .完全重合的两个三角形叫做 全等三角形 .一个图形经过 平移、翻折、旋转 后位置变化了,但形状‘大小都没有改变,即平移、翻折、旋转前后的图形 全等 . ( http: / / www.21cnjy.com )把两个全等三角形重合在一起, 重合的顶点 叫做对应顶点, 重合的边 叫做对应边, 重合的角 叫做对应角.2.全等三角形的性质全等三角形的对应边 相等 , 对应角 相等.全等用符号“≌”表示,读作“全等于”.
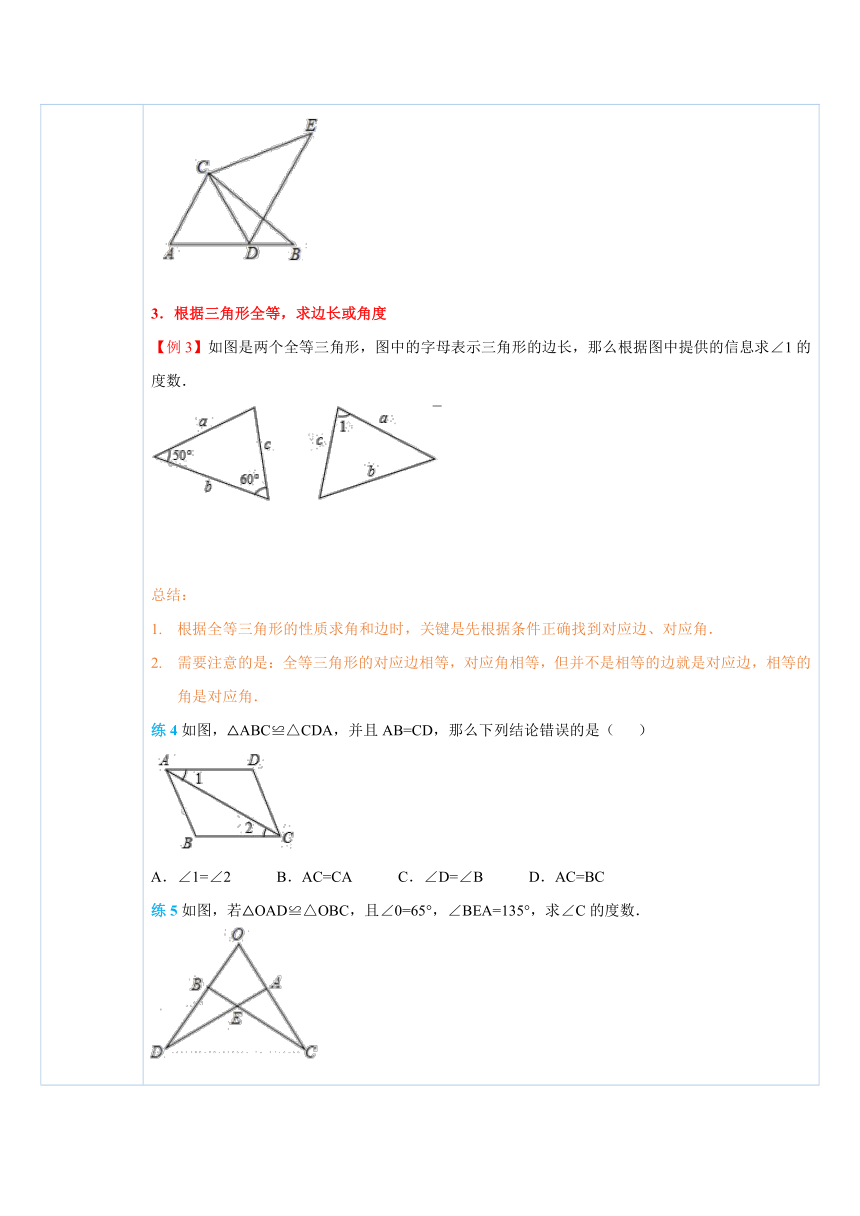
四、典例探究 扫一扫,有惊喜哦!1.全等三角形的相关概念【例1】下列说法正确的是( )A.形状相同的两个三角形全等 B.面积相等的两个三角形全等C.完全重合的两个三角形全等 D.所有的等边三角形全等总结:完全重合是全等三角形的本质属性.完全重合意味着这两个三角形形状相同且大小相等.将一个三角形经过平移、旋转、翻折得到的三角形与原三角形是全等三角形.练1 下列叙述中错误的是( )A.能够重合的图形称为全等图形B.全等图形的形状和大小都相同C.所有正方形都是全等图形D.形状和大小都相同的两个图形是全等图形2.已知三角形全等,找对应角、对应边【例2】如图,已知△ABC与△EBD全等,请指出其中的对应角和对应边. ( http: / / www.21cnjy.com )总结:已知两个三角形全等,我们根据定义:“把两 ( http: / / www.21cnjy.com )个全等三角形重合在一起,重合的点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角”,找出两个全等三角形的对应角及对应边.除了利用定义找全等三角形的对应角和对应边外,还有以下方法:(1)记两个三角形全等时,通常把对应顶点的字母写在对应的位置上,这样对应的两个字母为端点的线段是对应边,对应字母表示的角是对应角;(2)夹对应角的边是对应边,对应边的夹角是对应角.3. 还可用如下规律确定常见全等三角形的对应边和对应角:类型图例说明有公共边公共边是对应边,如图,△ABC≌△BAD, AB是公共边,AB与BA是对应边有公共角 ( http: / / www.21cnjy.com )公共角是对应角,如图,△ABC≌△ADE, ∠A是公共角,则∠BAC与∠DAE是对应角对顶角对顶角是对应角,如图,△ABC≌△ADE, ∠CAB与∠EAD时对顶角,故它们是对应角最长(短)与最长(短)边,最大(小)角与最(小)大角 ( http: / / www.21cnjy.com )两个全等三角形中,一对最长(短)边是对应边 ( http: / / www.21cnjy.com ),一对最大(小)角是对应角,如图,△ABC≌△A’B’C’, AC与A’C’为最长边,AB与A’B’为最短边,它们分别是对应边;∠B与∠B’是最大角,∠C与∠C’是最小角,它们分别是对应角练2如图,△ABC≌△DEF,点A与点D,点B与点E是对应顶点,写出这两个三角形的对应边和对应角. ( http: / / www.21cnjy.com )练3如图,△ACB≌△DCE,∠B与∠E是对应角,AB与DE是对应边,请写出其他对应边及对应角. ( http: / / www.21cnjy.com )3.根据三角形全等,求边长或角度【例3】如图是两个全等三角形,图中的字母表示三角形的边长,那么根据图中提供的信息求∠1的度数. ( http: / / www.21cnjy.com )总结:根据全等三角形的性质求角和边时,关键是先根据条件正确找到对应边、对应角.需要注意的是:全等三角形的对应边相等,对应角相等,但并不是相等的边就是对应边,相等的角是对应角.练4如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( ) ( http: / / www.21cnjy.com )A.∠1=∠2 B.AC=CA C.∠D=∠B D.AC=BC练5如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数. ( http: / / www.21cnjy.com )
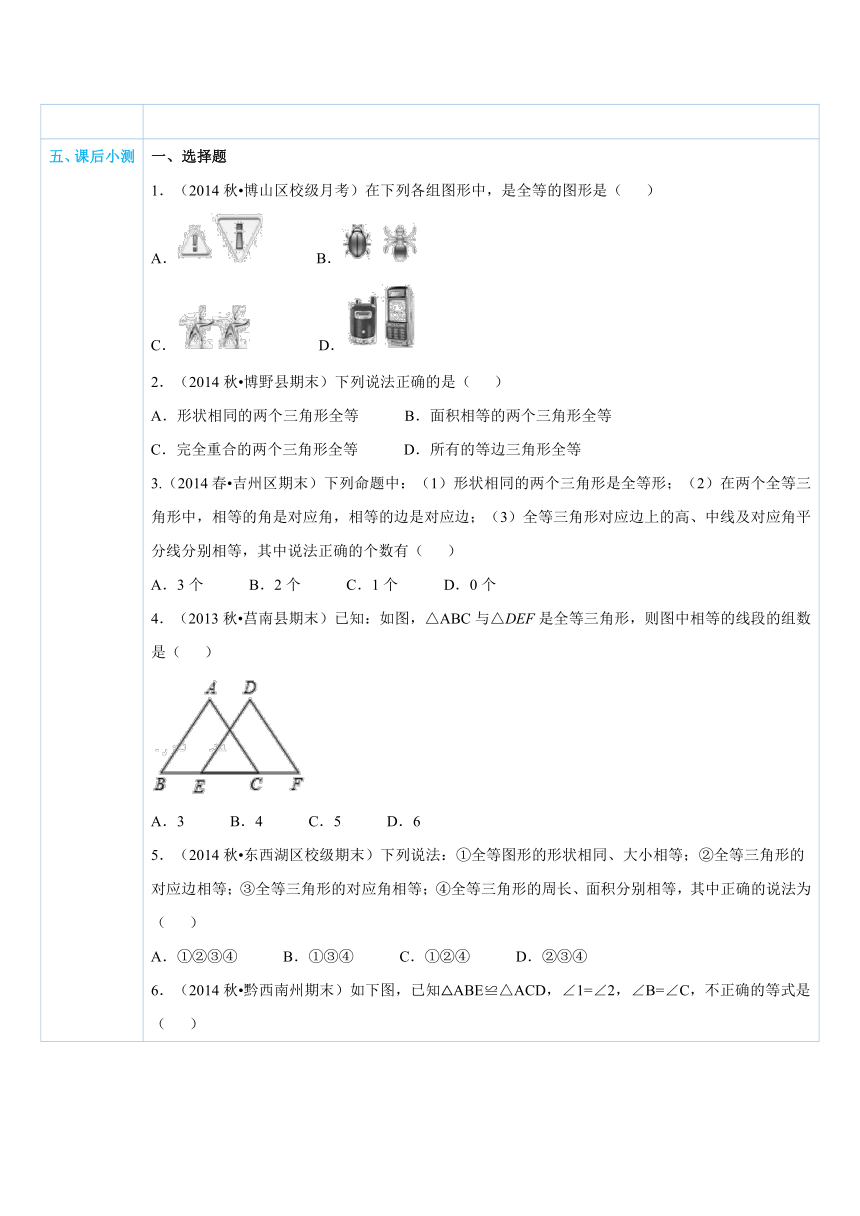
五、课后小测 一、选择题1.(2014秋 博山区校级月考)在下列各组图形中,是全等的图形是( )A. B.C. D.2.(2014秋 博野县期末)下列说法正确的是( )A.形状相同的两个三角形全等 B.面积相等的两个三角形全等C.完全重合的两个三角形全等 D.所有的等边三角形全等3.(2014春 吉州区期末)下列命题中: ( http: / / www.21cnjy.com )(1)形状相同的两个三角形是全等形;(2)在两个全等三角形中,相等的角是对应角,相等的边是对应边;(3)全等三角形对应边上的高、中线及对应角平分线分别相等,其中说法正确的个数有( )A.3个 B.2个 C.1个 D.0个4.(2013秋 莒南县期末)已知:如图,△ABC与△DEF是全等三角形,则图中相等的线段的组数是( ) ( http: / / www.21cnjy.com )A.3 B.4 C.5 D.65.(2014秋 东西湖区 ( http: / / www.21cnjy.com )校级期末)下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )A.①②③④ B.①③④ C.①②④ D.②③④6.(2014秋 黔西南州期末)如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( ) ( http: / / www.21cnjy.com )A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE7.(2014秋 河南期末)如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( ) ( http: / / www.21cnjy.com )A.40° B.35° C.30° D.25°二、填空题8.(2015春 丘北县校级月考)如果 ( http: / / www.21cnjy.com )△ABC≌△ADC,AB=AD,∠B=70°,BC=3cm,那么∠D=_____,DC=_____cm.9.(2015春 丘北县校级月考)若两个三角形全等,猜想它们对应的高、中线、角平分线的关系是______.10.(2014秋 昌乐县期末)如 ( http: / / www.21cnjy.com )图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC=______cm. ( http: / / www.21cnjy.com )11.(2013秋 新洲区期末)已 ( http: / / www.21cnjy.com )知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,则EF边上的高的长是_______cm.三、解答题12.(2013秋 本溪期末)在△ABC中, ( http: / / www.21cnjy.com )点A的坐标为(﹣1,1),点C的坐标为(﹣2,2),点B的坐标为(﹣5,1),如果△ABD与△ABC全等,求点D的坐标. ( http: / / www.21cnjy.com )13.(2014秋 利川市校级期中)如图,已知△EFG≌△NMH,∠F与∠M是对应角.(1)写出相等的线段与角.(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度. ( http: / / www.21cnjy.com )14.(2014秋 隆化县校级期中)(1)如图1,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.(2)如图2,若△OAD≌△OBC,且∠O=65°,∠C=20°,求∠OAD的度数. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据全等形的概念:能够完全重合的两个图形叫做全等形.
解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
点评:此题主要考查了全等图形,关键是掌握全等形的概念.
练1.【解析】能够完全重合的两个图形叫做全等形,结合各选项进行判断即可.
解:A、能够重合的图形称为全等图形,说法正确,故本选项错误;
B、全等图形的形状和大小都相同,说法正确,故本选项错误;
C、所有正方形不一定都是全等图形,说法错误,故本选项正确;
D、形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选C.
【例2】【解析】观察可知,这两个三角形可以通过旋转得到,AB和EB最短,DE和CA最长,它们分别是对应边;相应地,DB和CB是对应边.
再根据“对应边所对对应角”,可得∠ABC和∠EBD,∠A和∠E,∠D和∠C分别是对应角.
也可依据“直角、钝角应先选”,先判断出对应角∠ABC和∠EBD,再逐步分析找出对应角和对应边.
所以,其中的对应角是:∠ABC和∠EBD,∠A和∠E,∠D和∠C.
其中的对应边是:AB和EB,DE和CA,DB和CB.
点评:本题考查了全等图形的知识,要求同学们掌握全等图形的定义及性质.
练2.【解析】∵△ABC≌△DEF,
∴对应角是∠BAC与∠EDF,∠ABC与∠DEF,∠C与∠F,
对应边是AB与DE,AC与DF,BC与EF.
练3.【解析】∵△ACB≌△DCE,
∴其他的对应边有:AC与DC,CB与CE;
其他的对应角有:∠ACB与∠DCE,∠CAB与∠CDE.
【例3】【解析】根据三角形内角和定理计算出∠2的度数,然后再根据全等三角形的对应角相等可得∠1=∠2=70°.
解:根据三角形内角和可得∠2=180°﹣50°﹣60°=70°,
因为两个三角形全等,
所以∠1=∠2=70°,
故答案为:70°.
( http: / / www.21cnjy.com )
点评:此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
练4.【解析】由△ABC≌ ( http: / / www.21cnjy.com )△CDA,并且AB=CD,AC和CA是公共边,可知∠1和∠2,∠D和∠B是对应角.全等三角形的对应角相等,因而前三个选项一定正确.AC和BC不是对应边,不一定相等.
解:∵△ABC≌△CDA,AB=CD,
∴∠1和∠2,∠D和∠B是对应角,
∴∠1=∠2,∠D=∠B,
∴AC和CA是对应边,而不是BC,
∴A、B、C正确,错误的结论是D.AC=BC.
故选D.
点评:本题主要考查了全等三角形性质;而根据已知条件正确找着对应边、对应角是正确解决本题的关键.
练5.【解析】根据全等三 ( http: / / www.21cnjy.com )角形对应角相等可得∠C=∠D,∠OBC=∠OAD,再根据三角形的内角和等于180°表示出∠OBC,然后利用四边形的内角和等于360°列方程求解即可.
解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
点评:本题考查了全等三角形的性质,三角形的内角和定理,四边形的内角和定理,熟记性质与定理并列出关于∠C的方程是解题的关键.
课后小测答案:
一、选择题
1.【解析】能够完全重合的两个图形叫做全等形.只有选项C能够完全重合,A中大小不一致,B,D中形状不同.
解:由全等形的概念可以判断:C中图形完全相同,符合全等形的要求,而A、B、D中图形很明显不相同,A中大小不一致,B,D中形状不同.
故选C.
点评:本题考查的是全等形的识别,属于较容易的基础题.
2.【解析】根据全等形的概念:能够完全重合的两个图形叫做全等形,以及全等三角形的判定定理可得答案.
解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
点评:此题主要考查了全等图形,关键是掌握全等形的概念.
3.【解析】根据全等三角形的概念:能够 ( http: / / www.21cnjy.com )完全重合的图形是全等图形,及全等图形性质:全等图形的对应边、对应角分别相等,分别对每一项进行分析即可得出正确的命题个数.
解:(1)形状相同、大小相等的两个三角形是全等形,而原说法没有指出大小相等这一点,故(1)错误;
(2)在两个全等三角形中,对应角相等,对应边相等,而非相等的角是对应角,相等的边是对应边,故(2)错误;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等,故(3)正确.
综上可得只有(3)正确.
故选:C.
点评:本题考查了全等三角形的概念和全等三角形的性质,在解题时要注意灵活应用全等三角形的性质和定义是本题的关键.
4.【解析】△ABC≌△DEF,有三组对应边相等,在线段BF上,利用线段的和差关系可得BE=CF.
解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
∴BC﹣EC=EF﹣EC,
即BE=CF,有四组相等线段,
故选B.
点评:本题考查了全等三角形的性质,线段的和差关系,做题时要找全面,不要漏了.
5.【解析】根据全等形和全等三角形的概念知进行做题,对选项逐一进行验证,符合性质的是正确的,与性质、定义相矛盾的是错误的.
解:由全等三角形的概念可知:全等的图形 ( http: / / www.21cnjy.com )是完全重合的,所以①全等图形的形状相同、大小相等是正确的;重合则对应边、对应角是相等的,周长与面积也分别相等,所以①②③④都正确的
故选A.
点评:本题考查了全等形的概念和三角 ( http: / / www.21cnjy.com )形全等的性质:1、能够完全重合的两个图形叫做全等形,2、全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的周长、面积分别相等,做题时要细心体会.
6.【解析】根据全等三角形的性质,全等三角形的对应边相等,全等三角形的对应角相等,即可进行判断.
解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选D.
点评:本题主要考查了全等三角形的性质,根据已知的对应角正确确定对应边是解题的关键.
7.【解析】根据三角形的内角和定理列式求 ( http: / / www.21cnjy.com )出∠BAC,再根据全等三角形对应角相等可得∠DAE=∠BAC,然后根据∠EAC=∠DAE﹣∠DAC代入数据进行计算即可得解.
解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,
∴∠EAC=∠DAE﹣∠DAC,
=70°﹣35°,
=35°.
故选B.
点评:本题考查了全等三角形对应角相等的性质,熟记性质并准确识图是解题的关键.
二、填空题
8.【解析】根据全等三角形对应角相等,全等三角形对应边相等解答即可.
解:∵△ABC≌△ADC,
∴∠D=∠B=70°,
DC=BC=3cm.
故答案为:70°;3.
点评:本题考查了全等三角形的性质,对应顶点的字母写在对应位置上是准确确定出对应角和对应边的关键.
9.【解析】根据能够互相重合的两个三角形叫做全等三角形解答.
解:若两个三角形全等,则它们对应的高、中线、角平分线的关系是对应相等.
故答案为:对应相等.
点评:本题考查了全等三角形的性质,熟记性质是解题的关键.
10.【解析】根据△DEF周长是32 ( http: / / www.21cnjy.com )cm,DE=9cm,EF=13cm就可求出第三边DF的长,根据全等三角形的对应边相等,即可求得AC的长.
解:DF=32﹣DE﹣EF=10cm.
∵△ABC≌△DEF,∠E=∠B,
∴AC=DF=10cm.
点评:本题考查全等三角形的性质,解题时应注重识别全等三角形中的对应边,要根据对应角去找对应边.
11.【解析】本题还可根据全等三角形的对应边上的高相等,求出BC边上的高,即可得到EF边上的高.
解:∵△ABC≌△DEF
∴S△DEF=S△ABC=18cm
设EF边上的高为h,则 EF h=18
即×6×h=18,h=6
故答案为:6.
点评:本题考查全等三角形的面积相等的性质,解题时应注重识别全等三角形中的对应边.
三、解答题
12.【解析】分为三种情况:当△ABC≌△ABD时,当△ABC≌△BAD时,当△ABC≌△BAD时,画出图形,即可得出答案.
解:当△ABC≌△ABD时,D坐标为(﹣2,0);
当△ABC≌△BAD时,D坐标为(﹣4,0);
当△ABC≌△BAD时,D坐标为(﹣4,2);
故点D坐标是(﹣2,0)、(﹣4,0)、(﹣4,2).
( http: / / www.21cnjy.com )
点评:本题考查了全等三角形的性质的应用,注意:全等三角形的对应角相等,对应边相等,解此题的关键是能根据题意化成符合条件的所有图形.
13.【解析】(1)根据△EFG≌△NMH,∠F与∠M是对应角可得到两个三角形中对应相等的三边和三角;
(2)根据(1)中的对等关系即可得MN和HG的长度.
解:(1)∵△EFG≌△NMH,∠F与∠M是对应角,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm.
点评:本题考查了全等三角形全等的性质及比较线段的长短,熟练找出两个全等三角形的对应角、对应边是解此题的关键.
14.【解析】(1)连接AD并延长AD至点E,根据三角形外角性质求出∠BDC=∠C+∠CAB+∠B,代入求出即可;
(2)根据全等三角形的性质求出∠D,根据三角形内角和定理求出即可.
(1)解:如图,连接AD并延长AD至点E,
( http: / / www.21cnjy.com )
∵∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C,
∴∠BDC=∠CDE+∠BDE
=∠C+∠CAD+∠BAD+∠B
=∠BAC+∠B+∠C,
∵∠A=90°,∠B=21°,∠C=32°,
∴∠BDC=90°+21°+32°=143°;
(2)解:∵△OAD≌△OBC,∠C=20°,
∴∠D=∠C=20°,
∵∠O=65°,
∴∠OAD=180°﹣∠O﹣∠D=180°﹣65°﹣20°=95°.
点评:本题考查了全等三角形的性质,三角形内角和定理,三角形的外角性质的应用,主要考查学生运用定理进行推理和计算的能力.
二、知识回顾 1.观察图案,指出这些图案中形状与大小相同的图形. ( http: / / www.21cnjy.com )2.请你举出生活中形状、大小完全相同的例子.
三、新知讲解 1.全等三角形的相关概念能够完全重合的两个图形叫做 全等形 .完全重合的两个三角形叫做 全等三角形 .一个图形经过 平移、翻折、旋转 后位置变化了,但形状‘大小都没有改变,即平移、翻折、旋转前后的图形 全等 . ( http: / / www.21cnjy.com )把两个全等三角形重合在一起, 重合的顶点 叫做对应顶点, 重合的边 叫做对应边, 重合的角 叫做对应角.2.全等三角形的性质全等三角形的对应边 相等 , 对应角 相等.全等用符号“≌”表示,读作“全等于”.
四、典例探究 扫一扫,有惊喜哦!1.全等三角形的相关概念【例1】下列说法正确的是( )A.形状相同的两个三角形全等 B.面积相等的两个三角形全等C.完全重合的两个三角形全等 D.所有的等边三角形全等总结:完全重合是全等三角形的本质属性.完全重合意味着这两个三角形形状相同且大小相等.将一个三角形经过平移、旋转、翻折得到的三角形与原三角形是全等三角形.练1 下列叙述中错误的是( )A.能够重合的图形称为全等图形B.全等图形的形状和大小都相同C.所有正方形都是全等图形D.形状和大小都相同的两个图形是全等图形2.已知三角形全等,找对应角、对应边【例2】如图,已知△ABC与△EBD全等,请指出其中的对应角和对应边. ( http: / / www.21cnjy.com )总结:已知两个三角形全等,我们根据定义:“把两 ( http: / / www.21cnjy.com )个全等三角形重合在一起,重合的点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角”,找出两个全等三角形的对应角及对应边.除了利用定义找全等三角形的对应角和对应边外,还有以下方法:(1)记两个三角形全等时,通常把对应顶点的字母写在对应的位置上,这样对应的两个字母为端点的线段是对应边,对应字母表示的角是对应角;(2)夹对应角的边是对应边,对应边的夹角是对应角.3. 还可用如下规律确定常见全等三角形的对应边和对应角:类型图例说明有公共边公共边是对应边,如图,△ABC≌△BAD, AB是公共边,AB与BA是对应边有公共角 ( http: / / www.21cnjy.com )公共角是对应角,如图,△ABC≌△ADE, ∠A是公共角,则∠BAC与∠DAE是对应角对顶角对顶角是对应角,如图,△ABC≌△ADE, ∠CAB与∠EAD时对顶角,故它们是对应角最长(短)与最长(短)边,最大(小)角与最(小)大角 ( http: / / www.21cnjy.com )两个全等三角形中,一对最长(短)边是对应边 ( http: / / www.21cnjy.com ),一对最大(小)角是对应角,如图,△ABC≌△A’B’C’, AC与A’C’为最长边,AB与A’B’为最短边,它们分别是对应边;∠B与∠B’是最大角,∠C与∠C’是最小角,它们分别是对应角练2如图,△ABC≌△DEF,点A与点D,点B与点E是对应顶点,写出这两个三角形的对应边和对应角. ( http: / / www.21cnjy.com )练3如图,△ACB≌△DCE,∠B与∠E是对应角,AB与DE是对应边,请写出其他对应边及对应角. ( http: / / www.21cnjy.com )3.根据三角形全等,求边长或角度【例3】如图是两个全等三角形,图中的字母表示三角形的边长,那么根据图中提供的信息求∠1的度数. ( http: / / www.21cnjy.com )总结:根据全等三角形的性质求角和边时,关键是先根据条件正确找到对应边、对应角.需要注意的是:全等三角形的对应边相等,对应角相等,但并不是相等的边就是对应边,相等的角是对应角.练4如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( ) ( http: / / www.21cnjy.com )A.∠1=∠2 B.AC=CA C.∠D=∠B D.AC=BC练5如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014秋 博山区校级月考)在下列各组图形中,是全等的图形是( )A. B.C. D.2.(2014秋 博野县期末)下列说法正确的是( )A.形状相同的两个三角形全等 B.面积相等的两个三角形全等C.完全重合的两个三角形全等 D.所有的等边三角形全等3.(2014春 吉州区期末)下列命题中: ( http: / / www.21cnjy.com )(1)形状相同的两个三角形是全等形;(2)在两个全等三角形中,相等的角是对应角,相等的边是对应边;(3)全等三角形对应边上的高、中线及对应角平分线分别相等,其中说法正确的个数有( )A.3个 B.2个 C.1个 D.0个4.(2013秋 莒南县期末)已知:如图,△ABC与△DEF是全等三角形,则图中相等的线段的组数是( ) ( http: / / www.21cnjy.com )A.3 B.4 C.5 D.65.(2014秋 东西湖区 ( http: / / www.21cnjy.com )校级期末)下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )A.①②③④ B.①③④ C.①②④ D.②③④6.(2014秋 黔西南州期末)如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( ) ( http: / / www.21cnjy.com )A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE7.(2014秋 河南期末)如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( ) ( http: / / www.21cnjy.com )A.40° B.35° C.30° D.25°二、填空题8.(2015春 丘北县校级月考)如果 ( http: / / www.21cnjy.com )△ABC≌△ADC,AB=AD,∠B=70°,BC=3cm,那么∠D=_____,DC=_____cm.9.(2015春 丘北县校级月考)若两个三角形全等,猜想它们对应的高、中线、角平分线的关系是______.10.(2014秋 昌乐县期末)如 ( http: / / www.21cnjy.com )图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC=______cm. ( http: / / www.21cnjy.com )11.(2013秋 新洲区期末)已 ( http: / / www.21cnjy.com )知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,则EF边上的高的长是_______cm.三、解答题12.(2013秋 本溪期末)在△ABC中, ( http: / / www.21cnjy.com )点A的坐标为(﹣1,1),点C的坐标为(﹣2,2),点B的坐标为(﹣5,1),如果△ABD与△ABC全等,求点D的坐标. ( http: / / www.21cnjy.com )13.(2014秋 利川市校级期中)如图,已知△EFG≌△NMH,∠F与∠M是对应角.(1)写出相等的线段与角.(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度. ( http: / / www.21cnjy.com )14.(2014秋 隆化县校级期中)(1)如图1,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.(2)如图2,若△OAD≌△OBC,且∠O=65°,∠C=20°,求∠OAD的度数. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据全等形的概念:能够完全重合的两个图形叫做全等形.
解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
点评:此题主要考查了全等图形,关键是掌握全等形的概念.
练1.【解析】能够完全重合的两个图形叫做全等形,结合各选项进行判断即可.
解:A、能够重合的图形称为全等图形,说法正确,故本选项错误;
B、全等图形的形状和大小都相同,说法正确,故本选项错误;
C、所有正方形不一定都是全等图形,说法错误,故本选项正确;
D、形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选C.
【例2】【解析】观察可知,这两个三角形可以通过旋转得到,AB和EB最短,DE和CA最长,它们分别是对应边;相应地,DB和CB是对应边.
再根据“对应边所对对应角”,可得∠ABC和∠EBD,∠A和∠E,∠D和∠C分别是对应角.
也可依据“直角、钝角应先选”,先判断出对应角∠ABC和∠EBD,再逐步分析找出对应角和对应边.
所以,其中的对应角是:∠ABC和∠EBD,∠A和∠E,∠D和∠C.
其中的对应边是:AB和EB,DE和CA,DB和CB.
点评:本题考查了全等图形的知识,要求同学们掌握全等图形的定义及性质.
练2.【解析】∵△ABC≌△DEF,
∴对应角是∠BAC与∠EDF,∠ABC与∠DEF,∠C与∠F,
对应边是AB与DE,AC与DF,BC与EF.
练3.【解析】∵△ACB≌△DCE,
∴其他的对应边有:AC与DC,CB与CE;
其他的对应角有:∠ACB与∠DCE,∠CAB与∠CDE.
【例3】【解析】根据三角形内角和定理计算出∠2的度数,然后再根据全等三角形的对应角相等可得∠1=∠2=70°.
解:根据三角形内角和可得∠2=180°﹣50°﹣60°=70°,
因为两个三角形全等,
所以∠1=∠2=70°,
故答案为:70°.
( http: / / www.21cnjy.com )
点评:此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
练4.【解析】由△ABC≌ ( http: / / www.21cnjy.com )△CDA,并且AB=CD,AC和CA是公共边,可知∠1和∠2,∠D和∠B是对应角.全等三角形的对应角相等,因而前三个选项一定正确.AC和BC不是对应边,不一定相等.
解:∵△ABC≌△CDA,AB=CD,
∴∠1和∠2,∠D和∠B是对应角,
∴∠1=∠2,∠D=∠B,
∴AC和CA是对应边,而不是BC,
∴A、B、C正确,错误的结论是D.AC=BC.
故选D.
点评:本题主要考查了全等三角形性质;而根据已知条件正确找着对应边、对应角是正确解决本题的关键.
练5.【解析】根据全等三 ( http: / / www.21cnjy.com )角形对应角相等可得∠C=∠D,∠OBC=∠OAD,再根据三角形的内角和等于180°表示出∠OBC,然后利用四边形的内角和等于360°列方程求解即可.
解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
点评:本题考查了全等三角形的性质,三角形的内角和定理,四边形的内角和定理,熟记性质与定理并列出关于∠C的方程是解题的关键.
课后小测答案:
一、选择题
1.【解析】能够完全重合的两个图形叫做全等形.只有选项C能够完全重合,A中大小不一致,B,D中形状不同.
解:由全等形的概念可以判断:C中图形完全相同,符合全等形的要求,而A、B、D中图形很明显不相同,A中大小不一致,B,D中形状不同.
故选C.
点评:本题考查的是全等形的识别,属于较容易的基础题.
2.【解析】根据全等形的概念:能够完全重合的两个图形叫做全等形,以及全等三角形的判定定理可得答案.
解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
点评:此题主要考查了全等图形,关键是掌握全等形的概念.
3.【解析】根据全等三角形的概念:能够 ( http: / / www.21cnjy.com )完全重合的图形是全等图形,及全等图形性质:全等图形的对应边、对应角分别相等,分别对每一项进行分析即可得出正确的命题个数.
解:(1)形状相同、大小相等的两个三角形是全等形,而原说法没有指出大小相等这一点,故(1)错误;
(2)在两个全等三角形中,对应角相等,对应边相等,而非相等的角是对应角,相等的边是对应边,故(2)错误;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等,故(3)正确.
综上可得只有(3)正确.
故选:C.
点评:本题考查了全等三角形的概念和全等三角形的性质,在解题时要注意灵活应用全等三角形的性质和定义是本题的关键.
4.【解析】△ABC≌△DEF,有三组对应边相等,在线段BF上,利用线段的和差关系可得BE=CF.
解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
∴BC﹣EC=EF﹣EC,
即BE=CF,有四组相等线段,
故选B.
点评:本题考查了全等三角形的性质,线段的和差关系,做题时要找全面,不要漏了.
5.【解析】根据全等形和全等三角形的概念知进行做题,对选项逐一进行验证,符合性质的是正确的,与性质、定义相矛盾的是错误的.
解:由全等三角形的概念可知:全等的图形 ( http: / / www.21cnjy.com )是完全重合的,所以①全等图形的形状相同、大小相等是正确的;重合则对应边、对应角是相等的,周长与面积也分别相等,所以①②③④都正确的
故选A.
点评:本题考查了全等形的概念和三角 ( http: / / www.21cnjy.com )形全等的性质:1、能够完全重合的两个图形叫做全等形,2、全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的周长、面积分别相等,做题时要细心体会.
6.【解析】根据全等三角形的性质,全等三角形的对应边相等,全等三角形的对应角相等,即可进行判断.
解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选D.
点评:本题主要考查了全等三角形的性质,根据已知的对应角正确确定对应边是解题的关键.
7.【解析】根据三角形的内角和定理列式求 ( http: / / www.21cnjy.com )出∠BAC,再根据全等三角形对应角相等可得∠DAE=∠BAC,然后根据∠EAC=∠DAE﹣∠DAC代入数据进行计算即可得解.
解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,
∴∠EAC=∠DAE﹣∠DAC,
=70°﹣35°,
=35°.
故选B.
点评:本题考查了全等三角形对应角相等的性质,熟记性质并准确识图是解题的关键.
二、填空题
8.【解析】根据全等三角形对应角相等,全等三角形对应边相等解答即可.
解:∵△ABC≌△ADC,
∴∠D=∠B=70°,
DC=BC=3cm.
故答案为:70°;3.
点评:本题考查了全等三角形的性质,对应顶点的字母写在对应位置上是准确确定出对应角和对应边的关键.
9.【解析】根据能够互相重合的两个三角形叫做全等三角形解答.
解:若两个三角形全等,则它们对应的高、中线、角平分线的关系是对应相等.
故答案为:对应相等.
点评:本题考查了全等三角形的性质,熟记性质是解题的关键.
10.【解析】根据△DEF周长是32 ( http: / / www.21cnjy.com )cm,DE=9cm,EF=13cm就可求出第三边DF的长,根据全等三角形的对应边相等,即可求得AC的长.
解:DF=32﹣DE﹣EF=10cm.
∵△ABC≌△DEF,∠E=∠B,
∴AC=DF=10cm.
点评:本题考查全等三角形的性质,解题时应注重识别全等三角形中的对应边,要根据对应角去找对应边.
11.【解析】本题还可根据全等三角形的对应边上的高相等,求出BC边上的高,即可得到EF边上的高.
解:∵△ABC≌△DEF
∴S△DEF=S△ABC=18cm
设EF边上的高为h,则 EF h=18
即×6×h=18,h=6
故答案为:6.
点评:本题考查全等三角形的面积相等的性质,解题时应注重识别全等三角形中的对应边.
三、解答题
12.【解析】分为三种情况:当△ABC≌△ABD时,当△ABC≌△BAD时,当△ABC≌△BAD时,画出图形,即可得出答案.
解:当△ABC≌△ABD时,D坐标为(﹣2,0);
当△ABC≌△BAD时,D坐标为(﹣4,0);
当△ABC≌△BAD时,D坐标为(﹣4,2);
故点D坐标是(﹣2,0)、(﹣4,0)、(﹣4,2).
( http: / / www.21cnjy.com )
点评:本题考查了全等三角形的性质的应用,注意:全等三角形的对应角相等,对应边相等,解此题的关键是能根据题意化成符合条件的所有图形.
13.【解析】(1)根据△EFG≌△NMH,∠F与∠M是对应角可得到两个三角形中对应相等的三边和三角;
(2)根据(1)中的对等关系即可得MN和HG的长度.
解:(1)∵△EFG≌△NMH,∠F与∠M是对应角,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm.
点评:本题考查了全等三角形全等的性质及比较线段的长短,熟练找出两个全等三角形的对应角、对应边是解此题的关键.
14.【解析】(1)连接AD并延长AD至点E,根据三角形外角性质求出∠BDC=∠C+∠CAB+∠B,代入求出即可;
(2)根据全等三角形的性质求出∠D,根据三角形内角和定理求出即可.
(1)解:如图,连接AD并延长AD至点E,
( http: / / www.21cnjy.com )
∵∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C,
∴∠BDC=∠CDE+∠BDE
=∠C+∠CAD+∠BAD+∠B
=∠BAC+∠B+∠C,
∵∠A=90°,∠B=21°,∠C=32°,
∴∠BDC=90°+21°+32°=143°;
(2)解:∵△OAD≌△OBC,∠C=20°,
∴∠D=∠C=20°,
∵∠O=65°,
∴∠OAD=180°﹣∠O﹣∠D=180°﹣65°﹣20°=95°.
点评:本题考查了全等三角形的性质,三角形内角和定理,三角形的外角性质的应用,主要考查学生运用定理进行推理和计算的能力.
