【多媒体导学案】人教版数学八年级上册第12章第4课时全等三角形的判定(ASA,AAS)(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第4课时全等三角形的判定(ASA,AAS)(教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 82.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 19:34:43 | ||
图片预览



文档简介
一、学习目标 1.掌握三角形全等的判定定理“角边角”与“角角边”,并能用数学符号语言表示这两个判定定理;2.能利用这两个定理判定两个三角形全等,并能利用这两个定理进行简单的推理与计算.;3.会选择合适的判定定理证明三角形全等.
二、知识回顾 我们已经学了哪几种判定三角形全等的方法?请写出来:SSS: 三边对应相等的两个三角形全等. SAS: 两边和它们的夹角对应相等的两个三角形全等.
三、新知讲解 1.ASA 两角和它们的夹边 分别相等的两个三角形全等,简称角边角或ASA.▲如下图,已知∠D=∠E,AD=AE,∠1=∠2. ( http: / / www.21cnjy.com )求证:△ABD≌△ACE.证明:∵∠1=∠2( 已知 )∴∠1+ ∠CAD =∠2+ ∠CAD ( 相等的角加同一个角仍相等 )即∠BAD=∠CAE在△ABD和△ACE中,∠D=∠E( 已知 )AD=AE( 已知 ) ∠BAD=∠CAE (等量相加)∴△ABD≌△ACE( ASA ).2.AAS 两个角和其中一个角的对边 分别相等的两个三角形全等,简称角角边或AAS.▲如图:D在AB上,E在AC上,DC=EB,∠C=∠B. ( http: / / www.21cnjy.com )求证:△ACD≌△ABE.证明:在△ACD和△ABE中. ∠C=∠B (已知)∠A=∠A( 公共角 )DC=EB( 已知 )∴△ACD≌△ABE( AAS ).
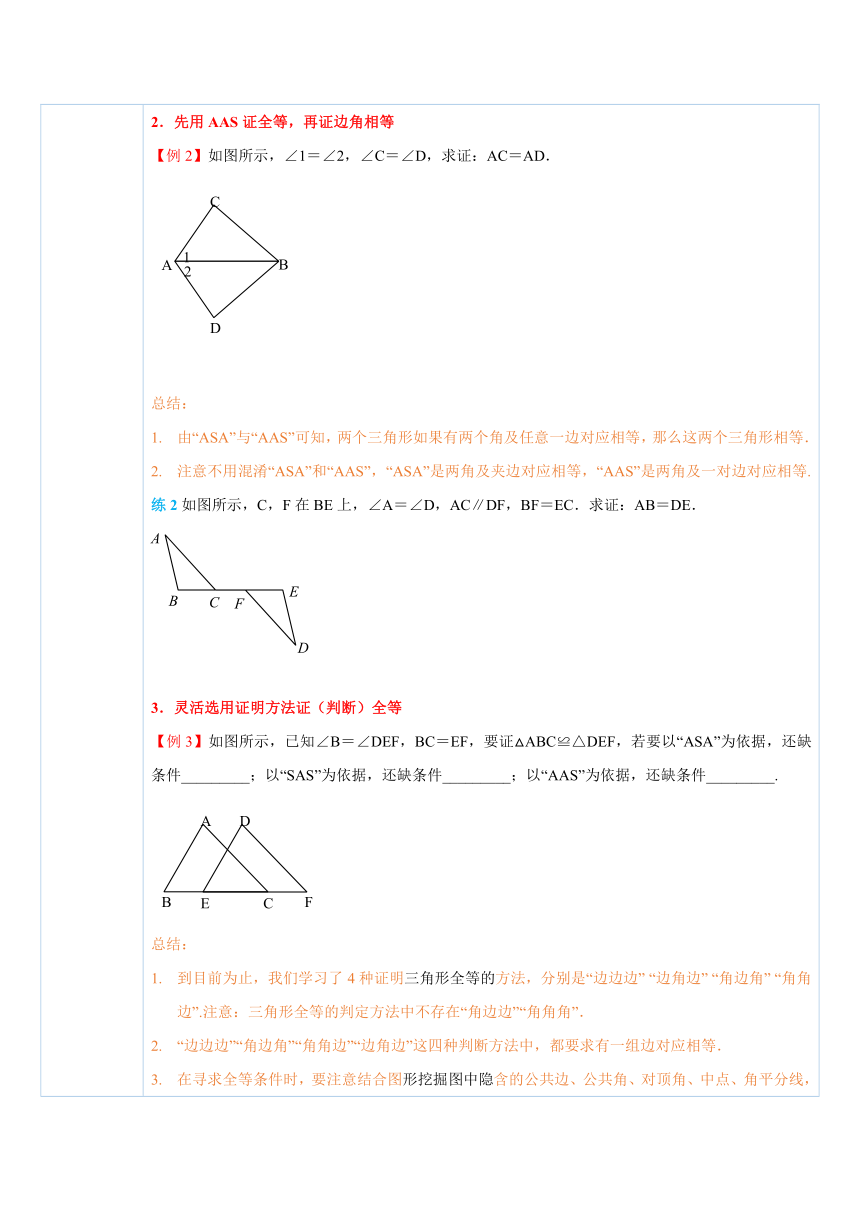
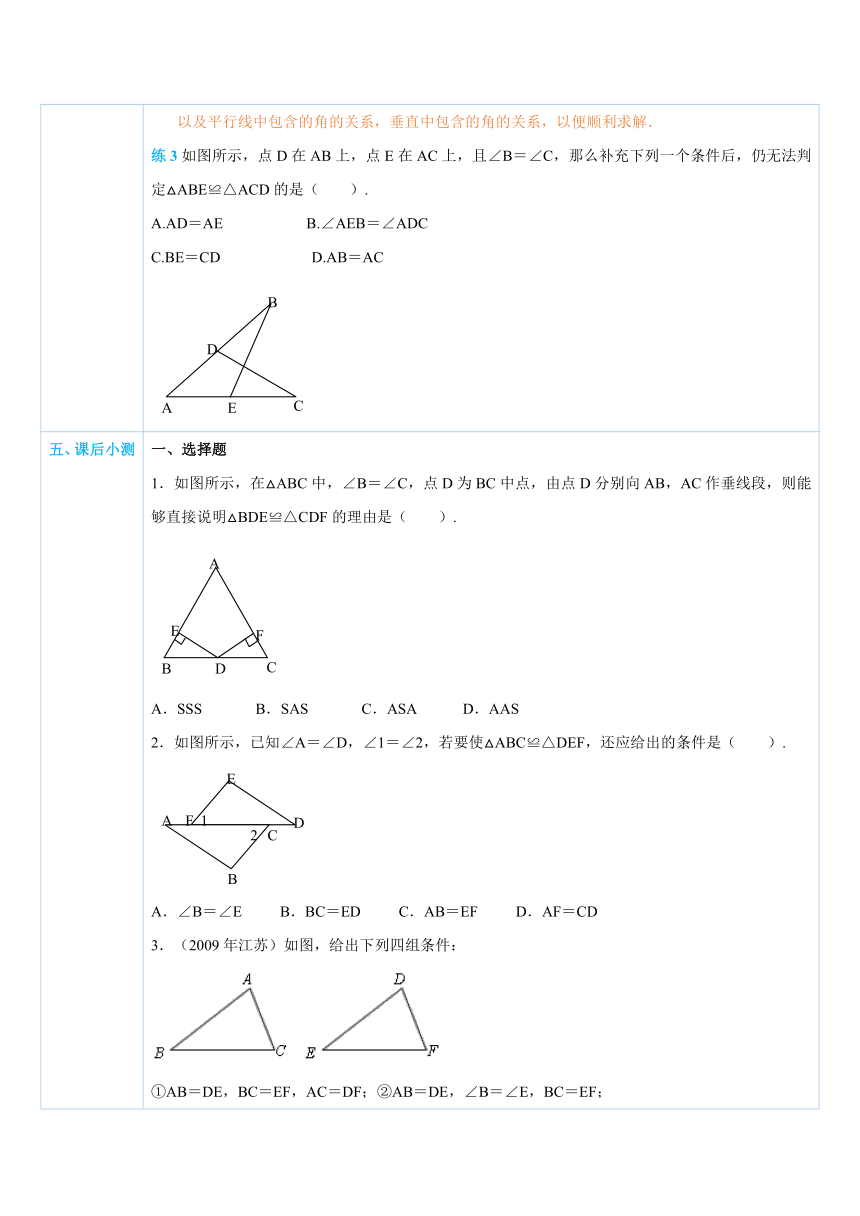
四、典例探究 扫一扫,有惊喜哦!1.先用ASA证全等,再证边角相等【例1】如图所示,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.求证:BO=DO.总结:全等三角形的对应边相等,对应角相等,所以证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明这两个三角形全等来解决.练1如图所示,在△ABC中,点O为AB的中点,AD∥BC,过点O的直线分别交AD,BC于点D,E,求证:OD=OE.2.先用AAS证全等,再证边角相等【例2】如图所示,∠1=∠2,∠C=∠D,求证:AC=AD.总结:由“ASA”与“AAS”可知,两个三角形如果有两个角及任意一边对应相等,那么这两个三角形相等.注意不用混淆“ASA”和“AAS”,“ASA”是两角及夹边对应相等,“AAS”是两角及一对边对应相等.练2如图所示,C,F在BE上,∠A=∠D,AC∥DF,BF=EC.求证:AB=DE.3.灵活选用证明方法证(判断)全等【例3】如图所示,已知∠B=∠DEF,B ( http: / / www.21cnjy.com )C=EF,要证△ABC≌△DEF,若要以“ASA”为依据,还缺条件_________;以“SAS”为依据,还缺条件_________;以“AAS”为依据,还缺条件_________.总结:到目前为止,我们学习了4种证明三角形全等的 ( http: / / www.21cnjy.com )方法,分别是“边边边” “边角边” “角边角” “角角边”.注意:三角形全等的判定方法中不存在“角边边”“角角角”.“边边边”“角边角”“角角边”“边角边”这四种判断方法中,都要求有一组边对应相等.在寻求全等条件时,要注意结合图形挖掘图中隐 ( http: / / www.21cnjy.com )含的公共边、公共角、对顶角、中点、角平分线,以及平行线中包含的角的关系,垂直中包含的角的关系,以便顺利求解.练3如图所示,点D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ).A.AD=AE B.∠AEB=∠ADCC.BE=CD D.AB=AC
五、课后小测 一、选择题1.如图所示,在△ABC中 ( http: / / www.21cnjy.com ),∠B=∠C,点D为BC中点,由点D分别向AB,AC作垂线段,则能够直接说明△BDE≌△CDF的理由是( ).A.SSS B.SAS C.ASA D.AAS2.如图所示,已知∠A=∠D,∠1=∠2,若要使△ABC≌△DEF,还应给出的条件是( ).A.∠B=∠E B.BC=ED C.AB=EF D.AF=CD3.(2009年江苏)如图,给出下列四组条件: ( http: / / www.21cnjy.com )①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有().A.1组 B.2组 C.3组 D.4组二、填空题4.如图所示,AB∥CD,OB=OD,则由“ASA”可以直接判定△______≌△___________.5.如图所示,在△ABC中,AD⊥BC ( http: / / www.21cnjy.com ),CE⊥AB,垂足分别为点D,E,AD,CE交于点H,已知EH=EB=3,AE=4,则CH的长是___________. ( http: / / www.21cnjy.com )三、解答题6.(2009年武汉市)如图所示,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.7.如图所示,已知∠B=∠E,∠BAD=∠EAC,AC=AD,求证:AB=AE.8.如图所示,BF⊥AC,DE⊥AC,垂足分别为点F,E,BF=DE,∠B=∠D,求证:AE=CF.9.如图,将△BOD绕点O旋转18 ( http: / / www.21cnjy.com )0°后得到△AOC,再过点O任意画一条与AC,BD都相交的直线MN,交点分别为M和N.试问:线段OM=ON成立吗?若成立,请进行证明;若不成立,请说明理由. ( http: / / www.21cnjy.com )10.如图所示,直角三角形ABC的直角顶点C置于直线上,AC=BC,现过A,B两点分别作直线的垂线,垂足分别为点D,E.图10(1)请你在图中找出一对全等三角形,并写出证明过程;(2)若BE=3,DE=5,求AD的长.
典例探究答案:
【例1】【解析】先用“ASA”证明△ABC≌△ADC,得出AB=AD,再用“SAS”证明△ABO≌△ADO,可得出结论.
证明:在△ABC和△ADC中,
∴△ABC≌△ADC(ASA).
∴AB=AD.
在△ABO与△ADO中,
△ACO≌△ADO(SAS).
∴BO=DO.
练1.【解析】∵点O为AB的中点,∴AO=BO.
∵AD∥BC,∴∠ADO=∠BEO,∠DAO=∠EBO.
在△AOD与△BOE中,
∴△AOD≌△BOE(AAS).
∴OD=OE.
【例2】【解析】先利用AAS证明两三角形全等,再根据全等三角形的性质得出AC=AD.
证明:在△ACB与△ADB中,
∴△ACB≌△ADB(AAS).
∴AC=AD.
练2.【解析】先利用平行证明角相等,再用等量相减的思想证明BC=EF,应用AAS可得△ABC≌△DEF,进而得出结论.
证明:∵AC∥DF,
∴∠ACE=∠DFB.
又∵∠ACE+∠ACB=180°,∠DFB+∠DFE=180°,
∴∠ACB=∠DFE.
又BF=EC,∴BF-CF=EC-CF,即BC=EF.
在△ABC与△DEF中,
∴△ABC≌△DEF(AAS).
∴AB=DE.
【例3】【解析】已知一组角和一组边 ( http: / / www.21cnjy.com )相等,要依据“ASA”证全等就要求夹已知边的另一组角相等,故填∠ACB=∠DFE;要依据“SAS”证全等就要求夹已知角的另一组边相等,故填AB=DE;要依据“AAS”证全等就要求另一组角相等,故填∠A=∠D.
答案:∠ACB=∠DFE;AB=DE;∠A=∠D.
练3.【解析】选择A中的AD=AE,加上已知条件,可根据AAS证明△ABE≌△ACD;
选项B中给出∠AEB=∠ADC,加上已知条件,可得三对角相等,但三对角相等的三角形不一定全等;
选项C中的 BE=CD,加上已知条件,可根据AAS证明△ABE≌△ACD;
选项D中的 AB=AC,加上已知条件,可根据ASA证明△ABE≌△ACD;
故选:B.
课后小测答案:
一、选择题
1.【解析】已知两角和其中一角的对边相等,故用AAS可证全等;
故选:D.
2.已知两个角对应相等,只要再有任意一边对应相等即可;
故选:D.
3.①满足SSS,可证全等;②满足SAS,可证全等;③满足ASA,可证全等;④是两边和其中一边的对角对应相等,两三角形不一定全等.
故选:C.
二、填空题
4.AOB,COD.
5.【解析】∵∠AHE=∠CHD,利用和等角互余的两个角相等,
∴∠EAH=∠ECB
又∵∠AEH=∠CEB=90°
EH=EB
∴△AEH≌△CEB(AAS)
∴CE=AE=4,,EH=3,
∴CH=4-3=1
答案:1
三、解答题
6.【解析】利用平行线,可得两同位角相等,再利用等量相加得BC=EF,即可证两三角形全等.
证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BC=EF.
在△ABC与△DEF中,
∠B=∠DEF,BC=EF,∠ACB=∠F,
∴△ABC≌△DEF(ASA).
7.【解析】先证全等,再利用三角形的性质得出结论.
证明∵∠BAD=∠EAC,
∴∠BAD-∠CAD=∠EAC-∠CAD.
∴∠BAC=∠EAD,
在△ABC和△AED中,
∴△ABC≌△AED(AAS).
∴AB=AE.
8.【解析】∵BF⊥AC,DE⊥AC,∴∠DEC=∠BFA=90°.
在△BFA与△DEC中,
∴△BFA≌△DEC(ASA).
∴AF=CE.
∴AF+EF=CE+EF.
∴AE=CF.
9.【解析】OM=ON成立.理由是:
∵△BOD绕点O旋转180°后得到△AOC,
∴△BOD≌△AOC.
∴∠A=∠B,AO=BO.
又∵∠AOM=∠BON,
∴△AOM≌△BON(ASA).
∴OM=ON.
10.【解析】(1)△ACD≌△CBE,
证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°.
又∵AD⊥,∴∠CAD+∠ACD=90°.
∴∠BCE=∠CAD.
∵BE⊥,∴∠ADC=∠CEB=90°.
在△ACD与△CBE中,
∠CAD=∠BCE,∠ADC=∠CEB,AC=CB,
∴△ACD≌△CBE(AAS).
(2)由(1)可知△ACD≌△CBE,
∴AD=CE,CD=BE,
∴AD=CE=CD+DE=BE+DE=3+5=8.
D
C
B
A
O
1
2
3
4
A
D
B
E
C
O
A
C
D
B
1
2
A
B
C
F
E
D
A
D
B
E
F
C
B
A
C
D
E
A
B
D
C
E
F
A
D
E
B
F
1
2
C
A
D
C
B
O
C
E
B
F
D
A
A
B
C
D
E
D
C
E
F
A
B
A
C
D
F
E
B
二、知识回顾 我们已经学了哪几种判定三角形全等的方法?请写出来:SSS: 三边对应相等的两个三角形全等. SAS: 两边和它们的夹角对应相等的两个三角形全等.
三、新知讲解 1.ASA 两角和它们的夹边 分别相等的两个三角形全等,简称角边角或ASA.▲如下图,已知∠D=∠E,AD=AE,∠1=∠2. ( http: / / www.21cnjy.com )求证:△ABD≌△ACE.证明:∵∠1=∠2( 已知 )∴∠1+ ∠CAD =∠2+ ∠CAD ( 相等的角加同一个角仍相等 )即∠BAD=∠CAE在△ABD和△ACE中,∠D=∠E( 已知 )AD=AE( 已知 ) ∠BAD=∠CAE (等量相加)∴△ABD≌△ACE( ASA ).2.AAS 两个角和其中一个角的对边 分别相等的两个三角形全等,简称角角边或AAS.▲如图:D在AB上,E在AC上,DC=EB,∠C=∠B. ( http: / / www.21cnjy.com )求证:△ACD≌△ABE.证明:在△ACD和△ABE中. ∠C=∠B (已知)∠A=∠A( 公共角 )DC=EB( 已知 )∴△ACD≌△ABE( AAS ).
四、典例探究 扫一扫,有惊喜哦!1.先用ASA证全等,再证边角相等【例1】如图所示,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.求证:BO=DO.总结:全等三角形的对应边相等,对应角相等,所以证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明这两个三角形全等来解决.练1如图所示,在△ABC中,点O为AB的中点,AD∥BC,过点O的直线分别交AD,BC于点D,E,求证:OD=OE.2.先用AAS证全等,再证边角相等【例2】如图所示,∠1=∠2,∠C=∠D,求证:AC=AD.总结:由“ASA”与“AAS”可知,两个三角形如果有两个角及任意一边对应相等,那么这两个三角形相等.注意不用混淆“ASA”和“AAS”,“ASA”是两角及夹边对应相等,“AAS”是两角及一对边对应相等.练2如图所示,C,F在BE上,∠A=∠D,AC∥DF,BF=EC.求证:AB=DE.3.灵活选用证明方法证(判断)全等【例3】如图所示,已知∠B=∠DEF,B ( http: / / www.21cnjy.com )C=EF,要证△ABC≌△DEF,若要以“ASA”为依据,还缺条件_________;以“SAS”为依据,还缺条件_________;以“AAS”为依据,还缺条件_________.总结:到目前为止,我们学习了4种证明三角形全等的 ( http: / / www.21cnjy.com )方法,分别是“边边边” “边角边” “角边角” “角角边”.注意:三角形全等的判定方法中不存在“角边边”“角角角”.“边边边”“角边角”“角角边”“边角边”这四种判断方法中,都要求有一组边对应相等.在寻求全等条件时,要注意结合图形挖掘图中隐 ( http: / / www.21cnjy.com )含的公共边、公共角、对顶角、中点、角平分线,以及平行线中包含的角的关系,垂直中包含的角的关系,以便顺利求解.练3如图所示,点D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ).A.AD=AE B.∠AEB=∠ADCC.BE=CD D.AB=AC
五、课后小测 一、选择题1.如图所示,在△ABC中 ( http: / / www.21cnjy.com ),∠B=∠C,点D为BC中点,由点D分别向AB,AC作垂线段,则能够直接说明△BDE≌△CDF的理由是( ).A.SSS B.SAS C.ASA D.AAS2.如图所示,已知∠A=∠D,∠1=∠2,若要使△ABC≌△DEF,还应给出的条件是( ).A.∠B=∠E B.BC=ED C.AB=EF D.AF=CD3.(2009年江苏)如图,给出下列四组条件: ( http: / / www.21cnjy.com )①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有().A.1组 B.2组 C.3组 D.4组二、填空题4.如图所示,AB∥CD,OB=OD,则由“ASA”可以直接判定△______≌△___________.5.如图所示,在△ABC中,AD⊥BC ( http: / / www.21cnjy.com ),CE⊥AB,垂足分别为点D,E,AD,CE交于点H,已知EH=EB=3,AE=4,则CH的长是___________. ( http: / / www.21cnjy.com )三、解答题6.(2009年武汉市)如图所示,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.7.如图所示,已知∠B=∠E,∠BAD=∠EAC,AC=AD,求证:AB=AE.8.如图所示,BF⊥AC,DE⊥AC,垂足分别为点F,E,BF=DE,∠B=∠D,求证:AE=CF.9.如图,将△BOD绕点O旋转18 ( http: / / www.21cnjy.com )0°后得到△AOC,再过点O任意画一条与AC,BD都相交的直线MN,交点分别为M和N.试问:线段OM=ON成立吗?若成立,请进行证明;若不成立,请说明理由. ( http: / / www.21cnjy.com )10.如图所示,直角三角形ABC的直角顶点C置于直线上,AC=BC,现过A,B两点分别作直线的垂线,垂足分别为点D,E.图10(1)请你在图中找出一对全等三角形,并写出证明过程;(2)若BE=3,DE=5,求AD的长.
典例探究答案:
【例1】【解析】先用“ASA”证明△ABC≌△ADC,得出AB=AD,再用“SAS”证明△ABO≌△ADO,可得出结论.
证明:在△ABC和△ADC中,
∴△ABC≌△ADC(ASA).
∴AB=AD.
在△ABO与△ADO中,
△ACO≌△ADO(SAS).
∴BO=DO.
练1.【解析】∵点O为AB的中点,∴AO=BO.
∵AD∥BC,∴∠ADO=∠BEO,∠DAO=∠EBO.
在△AOD与△BOE中,
∴△AOD≌△BOE(AAS).
∴OD=OE.
【例2】【解析】先利用AAS证明两三角形全等,再根据全等三角形的性质得出AC=AD.
证明:在△ACB与△ADB中,
∴△ACB≌△ADB(AAS).
∴AC=AD.
练2.【解析】先利用平行证明角相等,再用等量相减的思想证明BC=EF,应用AAS可得△ABC≌△DEF,进而得出结论.
证明:∵AC∥DF,
∴∠ACE=∠DFB.
又∵∠ACE+∠ACB=180°,∠DFB+∠DFE=180°,
∴∠ACB=∠DFE.
又BF=EC,∴BF-CF=EC-CF,即BC=EF.
在△ABC与△DEF中,
∴△ABC≌△DEF(AAS).
∴AB=DE.
【例3】【解析】已知一组角和一组边 ( http: / / www.21cnjy.com )相等,要依据“ASA”证全等就要求夹已知边的另一组角相等,故填∠ACB=∠DFE;要依据“SAS”证全等就要求夹已知角的另一组边相等,故填AB=DE;要依据“AAS”证全等就要求另一组角相等,故填∠A=∠D.
答案:∠ACB=∠DFE;AB=DE;∠A=∠D.
练3.【解析】选择A中的AD=AE,加上已知条件,可根据AAS证明△ABE≌△ACD;
选项B中给出∠AEB=∠ADC,加上已知条件,可得三对角相等,但三对角相等的三角形不一定全等;
选项C中的 BE=CD,加上已知条件,可根据AAS证明△ABE≌△ACD;
选项D中的 AB=AC,加上已知条件,可根据ASA证明△ABE≌△ACD;
故选:B.
课后小测答案:
一、选择题
1.【解析】已知两角和其中一角的对边相等,故用AAS可证全等;
故选:D.
2.已知两个角对应相等,只要再有任意一边对应相等即可;
故选:D.
3.①满足SSS,可证全等;②满足SAS,可证全等;③满足ASA,可证全等;④是两边和其中一边的对角对应相等,两三角形不一定全等.
故选:C.
二、填空题
4.AOB,COD.
5.【解析】∵∠AHE=∠CHD,利用和等角互余的两个角相等,
∴∠EAH=∠ECB
又∵∠AEH=∠CEB=90°
EH=EB
∴△AEH≌△CEB(AAS)
∴CE=AE=4,,EH=3,
∴CH=4-3=1
答案:1
三、解答题
6.【解析】利用平行线,可得两同位角相等,再利用等量相加得BC=EF,即可证两三角形全等.
证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BC=EF.
在△ABC与△DEF中,
∠B=∠DEF,BC=EF,∠ACB=∠F,
∴△ABC≌△DEF(ASA).
7.【解析】先证全等,再利用三角形的性质得出结论.
证明∵∠BAD=∠EAC,
∴∠BAD-∠CAD=∠EAC-∠CAD.
∴∠BAC=∠EAD,
在△ABC和△AED中,
∴△ABC≌△AED(AAS).
∴AB=AE.
8.【解析】∵BF⊥AC,DE⊥AC,∴∠DEC=∠BFA=90°.
在△BFA与△DEC中,
∴△BFA≌△DEC(ASA).
∴AF=CE.
∴AF+EF=CE+EF.
∴AE=CF.
9.【解析】OM=ON成立.理由是:
∵△BOD绕点O旋转180°后得到△AOC,
∴△BOD≌△AOC.
∴∠A=∠B,AO=BO.
又∵∠AOM=∠BON,
∴△AOM≌△BON(ASA).
∴OM=ON.
10.【解析】(1)△ACD≌△CBE,
证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°.
又∵AD⊥,∴∠CAD+∠ACD=90°.
∴∠BCE=∠CAD.
∵BE⊥,∴∠ADC=∠CEB=90°.
在△ACD与△CBE中,
∠CAD=∠BCE,∠ADC=∠CEB,AC=CB,
∴△ACD≌△CBE(AAS).
(2)由(1)可知△ACD≌△CBE,
∴AD=CE,CD=BE,
∴AD=CE=CD+DE=BE+DE=3+5=8.
D
C
B
A
O
1
2
3
4
A
D
B
E
C
O
A
C
D
B
1
2
A
B
C
F
E
D
A
D
B
E
F
C
B
A
C
D
E
A
B
D
C
E
F
A
D
E
B
F
1
2
C
A
D
C
B
O
C
E
B
F
D
A
A
B
C
D
E
D
C
E
F
A
B
A
C
D
F
E
B
