【多媒体导学案】人教版数学八年级上册第12章第7课时证全等的辅助线作法(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第7课时证全等的辅助线作法(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览



文档简介
一、学习目标 1.掌握全等三角形中常见辅助线的添加方法;2.提高解决实际问题的能力.
二、知识回顾 找全等三角形的方法可以从结论出发,寻找要证明的相等的两条线段(或两个角)分别在哪两个可能相等的三角形中;可以从已知条件出发,看已知条件可以确定哪两个三角形全等;可以从条件和结论综合考虑,看他们能确定哪两个三角形全等;若上述方法均不可行,可考虑添加辅助线,构造全等三角形.
三、新知讲解 三角形中常见辅助线的作法: ( http: / / www.21cnjy.com )(1)连接两点构造全等三角形例如:已知,AC、BD相交于O点,且AB=DC,AC=BD,求证:∠A=∠D. ( http: / / www.21cnjy.com )分析:要证∠A=∠D,可证它们所在的三角形△ABD和△DCO全等,而只有AB=DC和对顶角.两个条件,差一个条件,,难以证其全等,只 ( http: / / www.21cnjy.com )有另寻其它的三角形全等,由AB=DC,AC=BD,如连接BC,则△ABD和△DCO全等,所以,证得∠A=∠D.(2)作倍长中线构造全等三角形若遇到三角形的中线,可倍长中线,使延长线段与原中线长相等,构造全等三角形.利用的思维模式是全等变换中的“旋转”.例如:如下图:AD为 △ABC的中线,求证:AB+AC>2AD. ( http: / / www.21cnjy.com )分析:要证AB+AC>2AD,由图想到:A ( http: / / www.21cnjy.com )B+BD>AD,AC+CD>AD,所以有AB+AC+ BD+CD> AD +AD=2AD,左边比要证结论多BD+CD,故不能直接证出此题,而由2AD想到要构造2AD,即加倍中线,把所要证的线段转移到同一个三角形中去.因此,可作辅助线:延长AD至E,使DE=AD,连接BE,CE.(3)截长补短构造全等三角形在某条线段上截取一条线段与特定线段相等,或 ( http: / / www.21cnjy.com )是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.例如:如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD,求证:CD⊥AC. ( http: / / www.21cnjy.com )解析:(截长法)在AB上取中点F,连FD. ( http: / / www.21cnjy.com )△ADB是等腰三角形,F是底AB中点,由三线合一知:DF⊥AB,故∠AFD=90°△ADF≌△ADC(SAS)∠ACD=∠AFD=90°,即:CD⊥AC.(4)平移法过图形上某一点作特定的平行线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”.例如:如图,△ABC中,AB=AC,E是AB上一点,F是AC延长线上一点,连EF交BC于点D,若EB=CF.求证:DE=DF. ( http: / / www.21cnjy.com )分析:因为DE,DF所在的两个三角形△DEB与△DFC不可能全等,又知EB=CF,所以需通过添加辅助线进行相等线段的等量代换,过点E作EG∥CF,构造中心对称型全等三角形,再利用等腰三角形的性质,使问题得以解决.
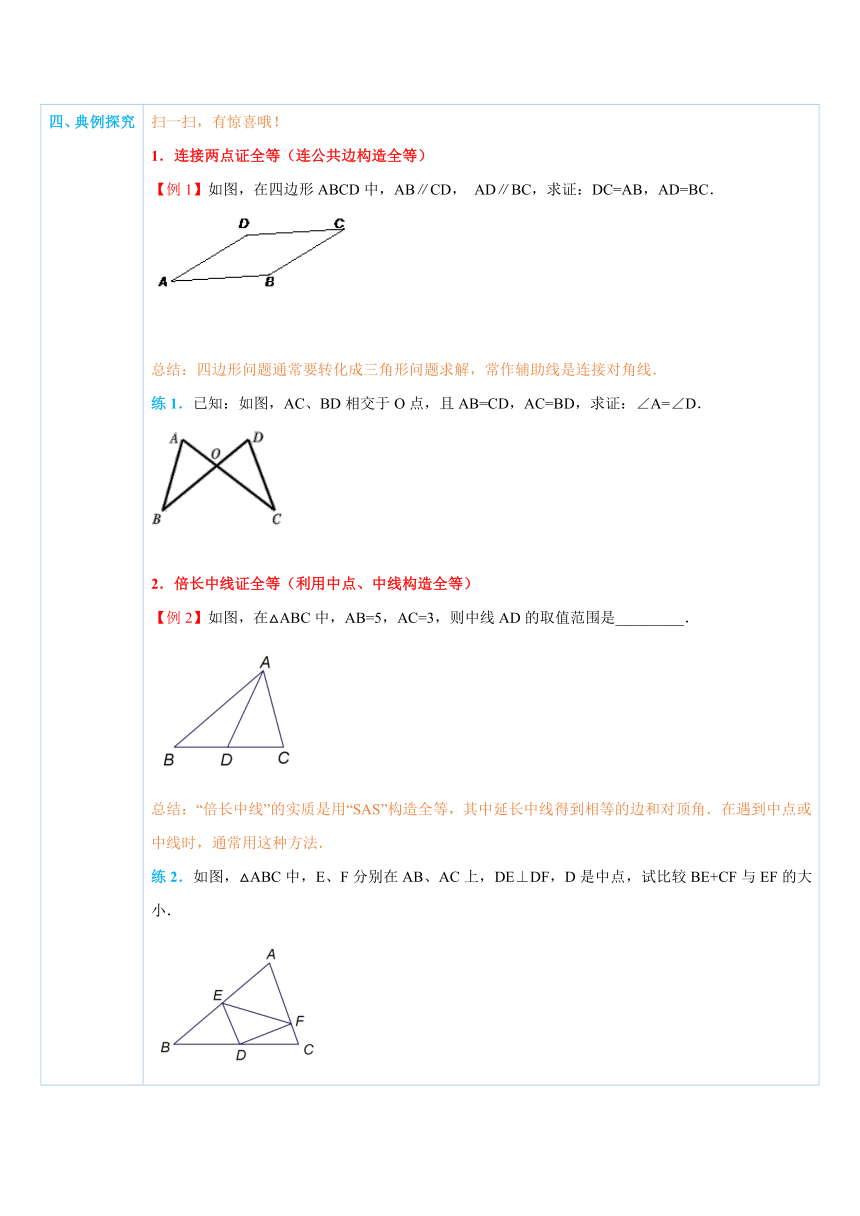
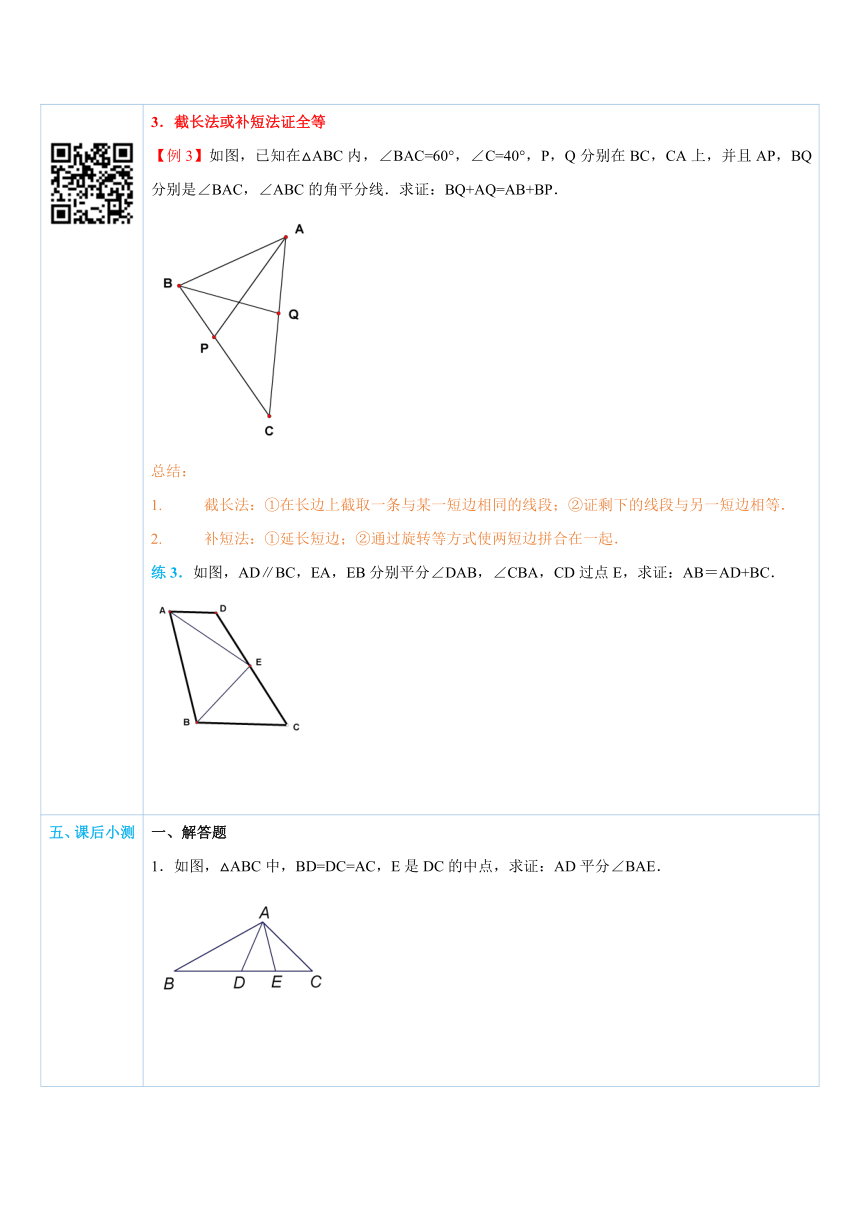
四、典例探究 ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.连接两点证全等(连公共边构造全等)【例1】如图,在四边形ABCD中,AB∥CD, AD∥BC,求证:DC=AB,AD=BC. ( http: / / www.21cnjy.com )总结:四边形问题通常要转化成三角形问题求解,常作辅助线是连接对角线.练1.已知:如图,AC、BD相交于O点,且AB=CD,AC=BD,求证:∠A=∠D. ( http: / / www.21cnjy.com )2.倍长中线证全等(利用中点、中线构造全等)【例2】如图,在△ABC中,AB=5,AC=3,则中线AD的取值范围是_________. ( http: / / www.21cnjy.com )总结:“倍长中线”的实质是用“SAS”构造全等,其中延长中线得到相等的边和对顶角.在遇到中点或中线时,通常用这种方法.练2.如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小. ( http: / / www.21cnjy.com )3.截长法或补短法证全等【例3】如图,已知在△ABC内,∠BA ( http: / / www.21cnjy.com )C=60°,∠C=40°,P,Q分别在BC,CA上,并且AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP. ( http: / / www.21cnjy.com )总结:截长法:①在长边上截取一条与某一短边相同的线段;②证剩下的线段与另一短边相等.补短法:①延长短边;②通过旋转等方式使两短边拼合在一起.练3.如图,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC. ( http: / / www.21cnjy.com )
五、课后小测 一、解答题1.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE. ( http: / / www.21cnjy.com )2.如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°. ( http: / / www.21cnjy.com )3.如图在△ABC中,AB>AC,∠1=∠2,P为AD上任意一点,求证:AB-AC>PB-PC. ( http: / / www.21cnjy.com )4.如图2,AD为△ABC的角平分线,AB>AC,求证:AB-AC>BD-DC. ( http: / / www.21cnjy.com )5.如图,△ABC是边长为3的等边 ( http: / / www.21cnjy.com )三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,求△AMN的周长. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】可连接BD,证明△ADB≌△CBD,进而获得结论.
证明:如图,连接BD.
( http: / / www.21cnjy.com )
∵AB∥CD, AD∥BC,
∴∠1=∠2,∠3=∠4.
在△ADB和△CBD中,
∴△ADEB≌△CBD(ASA).
∴DC=AB,AD=BC.
练1.【解析】根据已知条件证不出全等三角形,也证不出∠A=∠D.
连接BC,
( http: / / www.21cnjy.com )
在△ABC和△DBC中,
AB=CD(已知),
AC=BD(已知),
BC=BC(公共边),
∴△ABC≌△DBC.
∴∠A=∠D.
【例2】【解析】延长AD至E使AE=2AD,连接BE,CE.
( http: / / www.21cnjy.com )
AD=DE(作图)
∠ADC=∠EDB(对顶角)
CD=BD(D是中点)
∴△ADC≌△EDB(SAS)
∴BE=AC=3
由三角形三边关系知:
AB-BE <2AD即2<2AD<8,
故AD的取值范围是1练2.【解析】(倍长中线)延长FD至G使FG=2DF,连BG,EG;
( http: / / www.21cnjy.com )
由SAS可证:△FCD≌△GBD,
∴FD=GD,
在△EFD和△EGD中,
ED=ED(公共边)
∠EDF=∠EDG=90°(DE⊥DF)
FD=GD(已证)
∴△EFD≌△EGD
∴EG=EF
在△BEG中,由三角形性质知
EG故:EF【例3】【解析】证明:(补短法)延长AB至D,使BD=BP,连接DP,
( http: / / www.21cnjy.com )
在等腰三角形BPD中,可得∠BDP=40°,
从而∠BDP=40°=∠ACP,
在△ADP和△ACP中,
△ADP≌△ACP(AAS).
∴AD=AC,
又∠QBC=40°=∠QCB,
故BQ=QC.
∵BD=BP,
∴BQ+AQ=AB+BP.
练3.【解析】证明:(截长法)在AB上取点F,使AF=AD,连FE,
( http: / / www.21cnjy.com )
△ADE≌△AFE(SAS)
∠ADE=∠AFE,
∠ADE+∠BCE=180°
∠AFE+∠BFE=180°
故∠ECB=∠EFB
△FBE≌△CBE(AAS)
故有BF=BC
从而:AB=AD+BC.
课后小测答案:
一、解答题
1.【解析】证明:延长AE至G使AG=2AE,连BG,DG,
( http: / / www.21cnjy.com )
显然DG=AC,∠GDC=∠ACD,
由于DC=AC,故∠ADC=∠DAC
在△ADB与△ADG中,
BD=AC=DG,AD=AD,
∠ADB=∠ADC+∠ACD=∠ADC+∠GDC=∠ADG,
故△ADB≌△ADG,故有∠BAD=∠DAG,
即AD平分∠BAE.
2.【解析】(补短法)延长BA至F,使BF=BC,连FD,
( http: / / www.21cnjy.com )
△BDF≌△BDC(SAS)
故∠DFB=∠DCB,FD=DC
又AD=CD
故在等腰△BFD中
∠DFB=∠DAF
故有∠BAD+∠BCD=180°.
3.【解析】(补短法)延长AC至F,使AF=AB,连PD,
( http: / / www.21cnjy.com )
△ABP≌△AFP(SAS)
故BP=PF,
由三角形性质知:
PB-PC=PF-PC < CF=AF-AC=AB-AC.
4.【解析】可在AB上截取AE=A ( http: / / www.21cnjy.com )C,易得△ADE≌△ADC,从而将AB-AC转化为AB-AE,BD-DC转化为BD-DE,在△BDE中即可解决问题.
证明:在AB上截取AE=AC,连接DE,则BE=AB-AC.
在△ADE和△ADC中,
∴△ADE≌△ADC(SAS).
∴ DE=DC.
又∵BE>BD-DE,∴AB-AC>BD-DC.
点评:本题借助角平分线,在角的两边截取相同的线段构造“SAS”形式的全等三角形,使得问题顺利得解.对线段和差问题,常用截长补短法.
5.【解析】(图形补全法, “截长法”或“补短法”, 计算数值法) AC的延长线与BD的延长线交于点F,在线段CF上取点E,使CE=BM
∵△ABC为等边三角形,△BCD为等腰三角形 ( http: / / www.21cnjy.com ),且∠BDC=120°,
∴∠MBD=∠MBC+∠DBC=60°+30°=90°,
∠DCE=180°-∠ACD=180°-∠ABD=90°,
又∵BM=CE,BD=CD,
∴△CDE≌△BDM,
∴∠CDE=∠BDM,DE=DM,
∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC-∠MDN=120°-60°=60°,
∵在△DMN和△DEN中,
DM=DE
∠MDN=∠EDN=60°
DN=DN
∴△DMN≌△DEN,
∴MN=NE
∵在△DMA和△DEF中,
DM=DE
∠MDA=60°- ∠MDB=60°- ∠CDE=∠EDF (∠CDE=∠BDM)
∠DAM=∠DFE=30°
∴△DMN≌△DEN (AAS),
∴MA=FE
△AMN的周长为AN+MN+AM=AN+NE+EF=AF=6.
二、知识回顾 找全等三角形的方法可以从结论出发,寻找要证明的相等的两条线段(或两个角)分别在哪两个可能相等的三角形中;可以从已知条件出发,看已知条件可以确定哪两个三角形全等;可以从条件和结论综合考虑,看他们能确定哪两个三角形全等;若上述方法均不可行,可考虑添加辅助线,构造全等三角形.
三、新知讲解 三角形中常见辅助线的作法: ( http: / / www.21cnjy.com )(1)连接两点构造全等三角形例如:已知,AC、BD相交于O点,且AB=DC,AC=BD,求证:∠A=∠D. ( http: / / www.21cnjy.com )分析:要证∠A=∠D,可证它们所在的三角形△ABD和△DCO全等,而只有AB=DC和对顶角.两个条件,差一个条件,,难以证其全等,只 ( http: / / www.21cnjy.com )有另寻其它的三角形全等,由AB=DC,AC=BD,如连接BC,则△ABD和△DCO全等,所以,证得∠A=∠D.(2)作倍长中线构造全等三角形若遇到三角形的中线,可倍长中线,使延长线段与原中线长相等,构造全等三角形.利用的思维模式是全等变换中的“旋转”.例如:如下图:AD为 △ABC的中线,求证:AB+AC>2AD. ( http: / / www.21cnjy.com )分析:要证AB+AC>2AD,由图想到:A ( http: / / www.21cnjy.com )B+BD>AD,AC+CD>AD,所以有AB+AC+ BD+CD> AD +AD=2AD,左边比要证结论多BD+CD,故不能直接证出此题,而由2AD想到要构造2AD,即加倍中线,把所要证的线段转移到同一个三角形中去.因此,可作辅助线:延长AD至E,使DE=AD,连接BE,CE.(3)截长补短构造全等三角形在某条线段上截取一条线段与特定线段相等,或 ( http: / / www.21cnjy.com )是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.例如:如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD,求证:CD⊥AC. ( http: / / www.21cnjy.com )解析:(截长法)在AB上取中点F,连FD. ( http: / / www.21cnjy.com )△ADB是等腰三角形,F是底AB中点,由三线合一知:DF⊥AB,故∠AFD=90°△ADF≌△ADC(SAS)∠ACD=∠AFD=90°,即:CD⊥AC.(4)平移法过图形上某一点作特定的平行线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”.例如:如图,△ABC中,AB=AC,E是AB上一点,F是AC延长线上一点,连EF交BC于点D,若EB=CF.求证:DE=DF. ( http: / / www.21cnjy.com )分析:因为DE,DF所在的两个三角形△DEB与△DFC不可能全等,又知EB=CF,所以需通过添加辅助线进行相等线段的等量代换,过点E作EG∥CF,构造中心对称型全等三角形,再利用等腰三角形的性质,使问题得以解决.
四、典例探究 ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.连接两点证全等(连公共边构造全等)【例1】如图,在四边形ABCD中,AB∥CD, AD∥BC,求证:DC=AB,AD=BC. ( http: / / www.21cnjy.com )总结:四边形问题通常要转化成三角形问题求解,常作辅助线是连接对角线.练1.已知:如图,AC、BD相交于O点,且AB=CD,AC=BD,求证:∠A=∠D. ( http: / / www.21cnjy.com )2.倍长中线证全等(利用中点、中线构造全等)【例2】如图,在△ABC中,AB=5,AC=3,则中线AD的取值范围是_________. ( http: / / www.21cnjy.com )总结:“倍长中线”的实质是用“SAS”构造全等,其中延长中线得到相等的边和对顶角.在遇到中点或中线时,通常用这种方法.练2.如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小. ( http: / / www.21cnjy.com )3.截长法或补短法证全等【例3】如图,已知在△ABC内,∠BA ( http: / / www.21cnjy.com )C=60°,∠C=40°,P,Q分别在BC,CA上,并且AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP. ( http: / / www.21cnjy.com )总结:截长法:①在长边上截取一条与某一短边相同的线段;②证剩下的线段与另一短边相等.补短法:①延长短边;②通过旋转等方式使两短边拼合在一起.练3.如图,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC. ( http: / / www.21cnjy.com )
五、课后小测 一、解答题1.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE. ( http: / / www.21cnjy.com )2.如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°. ( http: / / www.21cnjy.com )3.如图在△ABC中,AB>AC,∠1=∠2,P为AD上任意一点,求证:AB-AC>PB-PC. ( http: / / www.21cnjy.com )4.如图2,AD为△ABC的角平分线,AB>AC,求证:AB-AC>BD-DC. ( http: / / www.21cnjy.com )5.如图,△ABC是边长为3的等边 ( http: / / www.21cnjy.com )三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,求△AMN的周长. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】可连接BD,证明△ADB≌△CBD,进而获得结论.
证明:如图,连接BD.
( http: / / www.21cnjy.com )
∵AB∥CD, AD∥BC,
∴∠1=∠2,∠3=∠4.
在△ADB和△CBD中,
∴△ADEB≌△CBD(ASA).
∴DC=AB,AD=BC.
练1.【解析】根据已知条件证不出全等三角形,也证不出∠A=∠D.
连接BC,
( http: / / www.21cnjy.com )
在△ABC和△DBC中,
AB=CD(已知),
AC=BD(已知),
BC=BC(公共边),
∴△ABC≌△DBC.
∴∠A=∠D.
【例2】【解析】延长AD至E使AE=2AD,连接BE,CE.
( http: / / www.21cnjy.com )
AD=DE(作图)
∠ADC=∠EDB(对顶角)
CD=BD(D是中点)
∴△ADC≌△EDB(SAS)
∴BE=AC=3
由三角形三边关系知:
AB-BE <2AD
故AD的取值范围是1
( http: / / www.21cnjy.com )
由SAS可证:△FCD≌△GBD,
∴FD=GD,
在△EFD和△EGD中,
ED=ED(公共边)
∠EDF=∠EDG=90°(DE⊥DF)
FD=GD(已证)
∴△EFD≌△EGD
∴EG=EF
在△BEG中,由三角形性质知
EG
( http: / / www.21cnjy.com )
在等腰三角形BPD中,可得∠BDP=40°,
从而∠BDP=40°=∠ACP,
在△ADP和△ACP中,
△ADP≌△ACP(AAS).
∴AD=AC,
又∠QBC=40°=∠QCB,
故BQ=QC.
∵BD=BP,
∴BQ+AQ=AB+BP.
练3.【解析】证明:(截长法)在AB上取点F,使AF=AD,连FE,
( http: / / www.21cnjy.com )
△ADE≌△AFE(SAS)
∠ADE=∠AFE,
∠ADE+∠BCE=180°
∠AFE+∠BFE=180°
故∠ECB=∠EFB
△FBE≌△CBE(AAS)
故有BF=BC
从而:AB=AD+BC.
课后小测答案:
一、解答题
1.【解析】证明:延长AE至G使AG=2AE,连BG,DG,
( http: / / www.21cnjy.com )
显然DG=AC,∠GDC=∠ACD,
由于DC=AC,故∠ADC=∠DAC
在△ADB与△ADG中,
BD=AC=DG,AD=AD,
∠ADB=∠ADC+∠ACD=∠ADC+∠GDC=∠ADG,
故△ADB≌△ADG,故有∠BAD=∠DAG,
即AD平分∠BAE.
2.【解析】(补短法)延长BA至F,使BF=BC,连FD,
( http: / / www.21cnjy.com )
△BDF≌△BDC(SAS)
故∠DFB=∠DCB,FD=DC
又AD=CD
故在等腰△BFD中
∠DFB=∠DAF
故有∠BAD+∠BCD=180°.
3.【解析】(补短法)延长AC至F,使AF=AB,连PD,
( http: / / www.21cnjy.com )
△ABP≌△AFP(SAS)
故BP=PF,
由三角形性质知:
PB-PC=PF-PC < CF=AF-AC=AB-AC.
4.【解析】可在AB上截取AE=A ( http: / / www.21cnjy.com )C,易得△ADE≌△ADC,从而将AB-AC转化为AB-AE,BD-DC转化为BD-DE,在△BDE中即可解决问题.
证明:在AB上截取AE=AC,连接DE,则BE=AB-AC.
在△ADE和△ADC中,
∴△ADE≌△ADC(SAS).
∴ DE=DC.
又∵BE>BD-DE,∴AB-AC>BD-DC.
点评:本题借助角平分线,在角的两边截取相同的线段构造“SAS”形式的全等三角形,使得问题顺利得解.对线段和差问题,常用截长补短法.
5.【解析】(图形补全法, “截长法”或“补短法”, 计算数值法) AC的延长线与BD的延长线交于点F,在线段CF上取点E,使CE=BM
∵△ABC为等边三角形,△BCD为等腰三角形 ( http: / / www.21cnjy.com ),且∠BDC=120°,
∴∠MBD=∠MBC+∠DBC=60°+30°=90°,
∠DCE=180°-∠ACD=180°-∠ABD=90°,
又∵BM=CE,BD=CD,
∴△CDE≌△BDM,
∴∠CDE=∠BDM,DE=DM,
∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC-∠MDN=120°-60°=60°,
∵在△DMN和△DEN中,
DM=DE
∠MDN=∠EDN=60°
DN=DN
∴△DMN≌△DEN,
∴MN=NE
∵在△DMA和△DEF中,
DM=DE
∠MDA=60°- ∠MDB=60°- ∠CDE=∠EDF (∠CDE=∠BDM)
∠DAM=∠DFE=30°
∴△DMN≌△DEN (AAS),
∴MA=FE
△AMN的周长为AN+MN+AM=AN+NE+EF=AF=6.
