【多媒体导学案】人教版数学八年级上册第12章第2课时全等三角形的判定(SSS)(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第2课时全等三角形的判定(SSS)(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 19:32:07 | ||
图片预览


文档简介
一、学习目标 1.掌握三角形全等的判定(SSS);2.初步体会尺规作图;3.掌握简单的证明格式.
二、知识回顾 ▲什么叫全等三角形? 能够重合的两个三角形叫全等三角形 .▲全等三角形的性质:全等三角形的 对应边相等 ,全等三角形的 对应角相等 .▲已知△ABC≌△DEF,找出其中相等的边与角 ( http: / / www.21cnjy.com ) ①AB=DE,②BC=EF,③CA=FD,④∠A=∠D,⑤∠B=∠E,⑥∠C=∠F. 满足这六个条件(三个角和三个边分别相等)可以保证△ABC≌△DEF? 可以
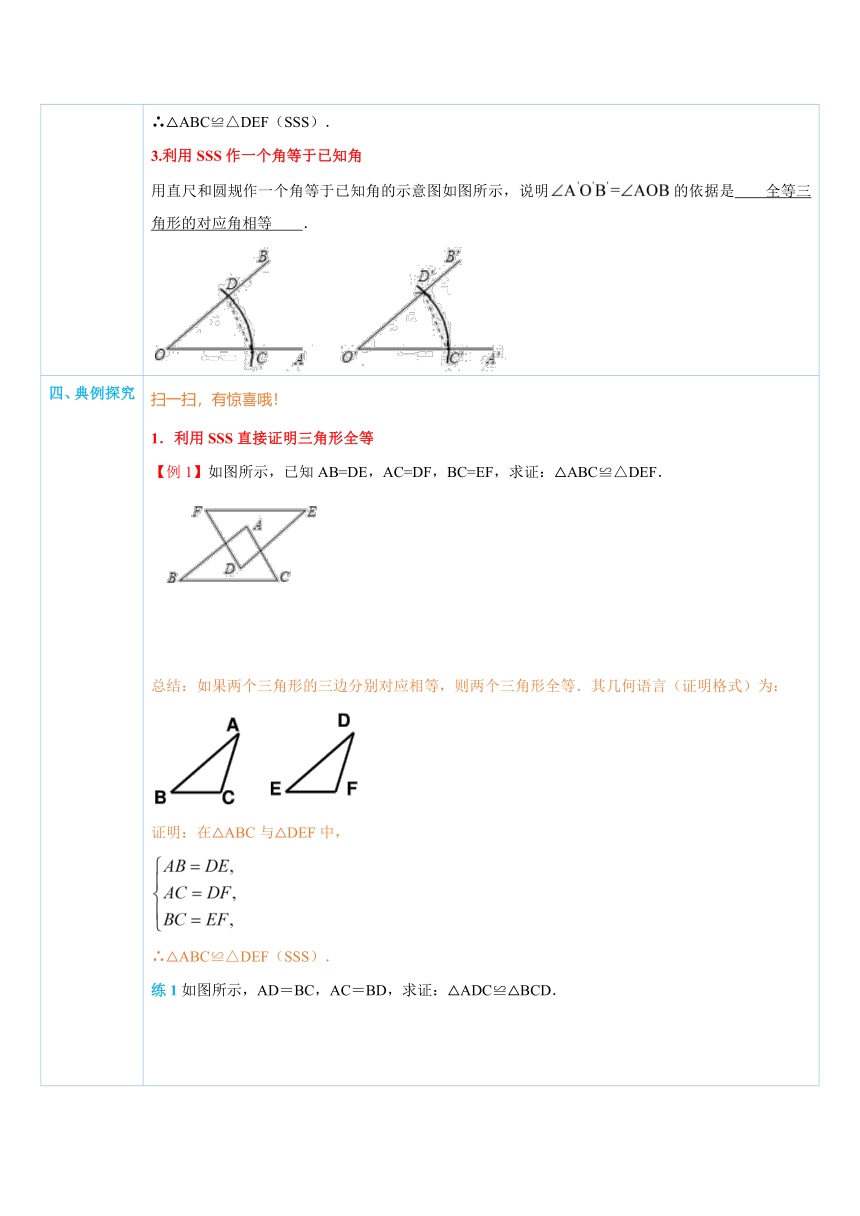
三、新知讲解 1.SSS 三边分别相等 的两个三角形全等(简称SSS).这个定理说明,只要三角形的三边长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有 稳定性 的原理.2.利用SSS证明三角形全等判断两个三角形全等的推理过程,叫做证明三角形全等.如下图,已知:△ABC与△DEF的三条边对应相等,求证:△ABC≌△DEF. ( http: / / www.21cnjy.com )证明:在△ABC与△DEF中, ∴△ABC≌△DEF(SSS).3.利用SSS作一个角等于已知角用直尺和圆规作一个角等于已知角的示意图如图所示,说明的依据是 全等三角形的对应角相等 . ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.利用SSS直接证明三角形全等【例1】如图所示,已知AB=DE,AC=DF,BC=EF,求证:△ABC≌△DEF. ( http: / / www.21cnjy.com )总结:如果两个三角形的三边分别对应相等,则两个三角形全等.其几何语言(证明格式)为: ( http: / / www.21cnjy.com )证明:在△ABC与△DEF中,∴△ABC≌△DEF(SSS).练1如图所示,AD=BC,AC=BD,求证:△ADC≌△BCD. ( http: / / www.21cnjy.com )2.先证明对应边相等,再证全等(利用中点、等量相加等)【例2】如图所示,在△ABC和△FED中,AD=FC,AB=FE,BC=ED,求证:△ABC≌△FED. ( http: / / www.21cnjy.com )总结:利用“SSS”证明两个三角形全等,有如下几种常见类型:(1)有公共边的两个三角形.(2)有公共线段的两个三角形,我们可以用等量相加或相减,推出两边相等.(3)含有中点的两个三角形,如图:AB=AC,D是BC的中点, ( http: / / www.21cnjy.com ),由中点的定义可得:BD=CD.继而可证△ABD≌△ACD.练2如图,已知AC=BD,0是AB、CD的中点,求证△AOC≌△BOD. ( http: / / www.21cnjy.com )3.先利用SSS证明三角形全等,继而证明边(角)相等,或求边(角)【例3】如图所示,AB=DC,AC=DB,求证:∠1=∠2. ( http: / / www.21cnjy.com )总结:要求证在两个不同三角形内的角相等,往往利用全等三角形的性质.当两个角所在的三角形不易证全等时,可以利用等量的和(差)相等,将问题转化.求证不在同一个三角形内的两边相等,同样可以利用全等三角形的性质.练3如图是“人”字形屋梁,AB=AC.现 ( http: / / www.21cnjy.com )在要在水平横梁BC上立一根垂直的支柱支撑屋梁,工人师傅取BC的中点D,然后在A,D之间竖支柱AD.那么这根AD符合“垂直”的要求吗?为什么? ( http: / / www.21cnjy.com )
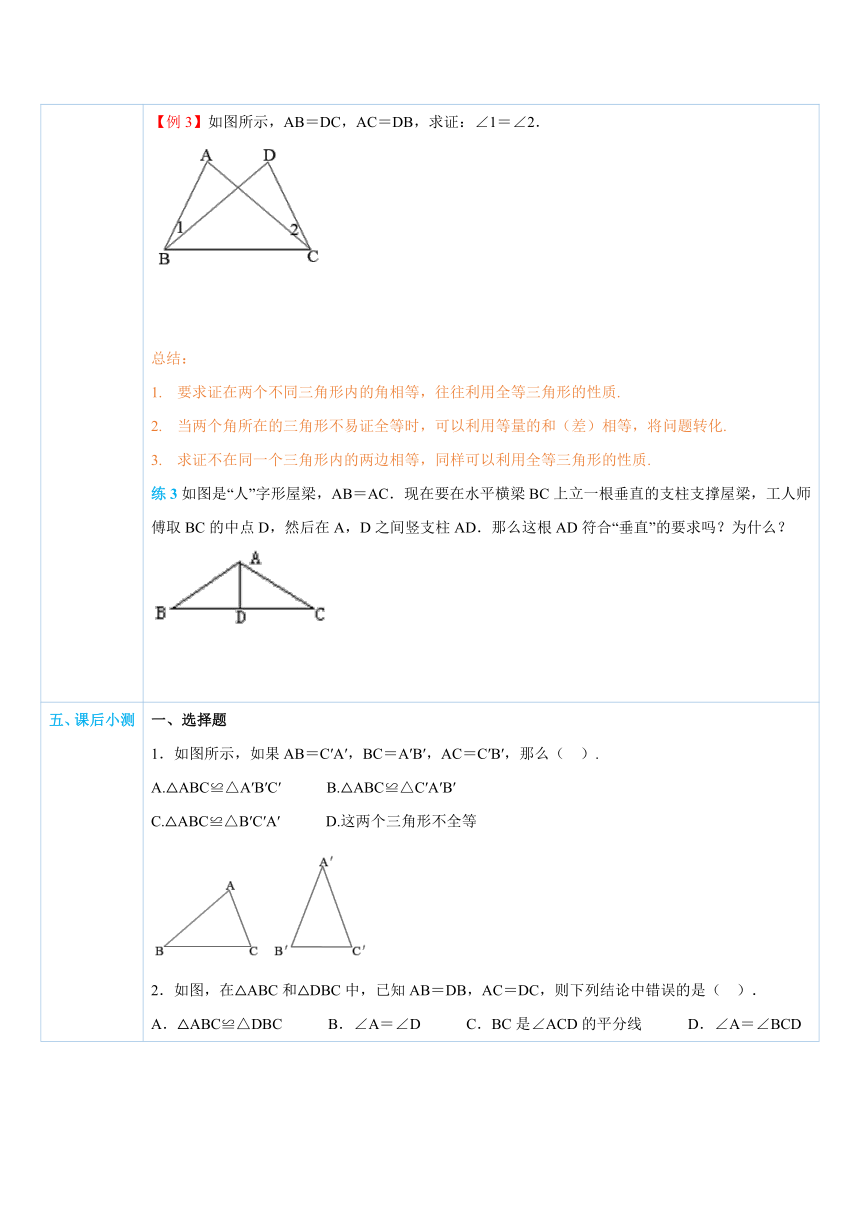
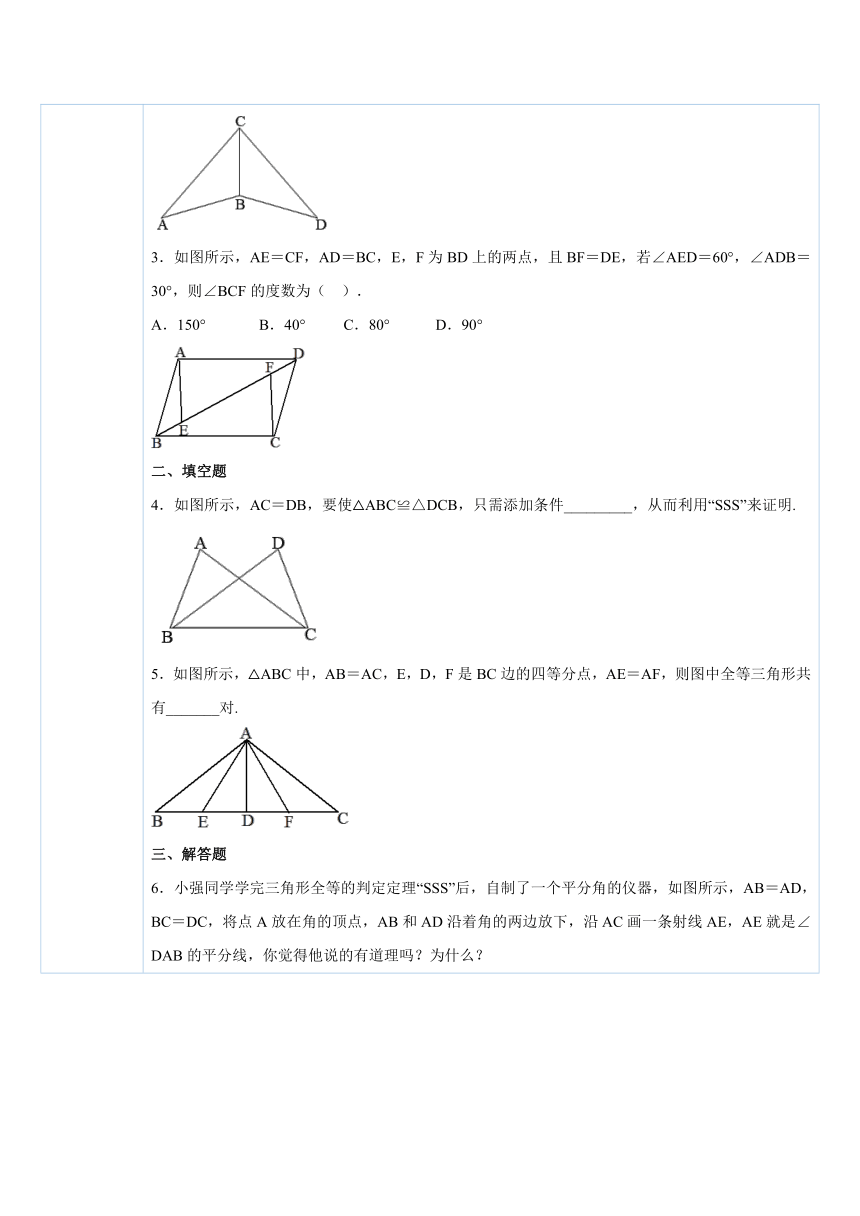
五、课后小测 一、选择题1.如图所示,如果AB=C′A′,BC=A′B′,AC=C′B′,那么( ).A.△ABC≌△A′B′C′ B.△ABC≌△C′A′B′C.△ABC≌△B′C′A′ D.这两个三角形不全等 ( http: / / www.21cnjy.com )2.如图,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( ).A.△ABC≌△DBC B.∠A=∠D C.BC是∠ACD的平分线 D.∠A=∠BCD ( http: / / www.21cnjy.com )3.如图所示,AE=CF,AD=BC,E, ( http: / / www.21cnjy.com )F为BD上的两点,且BF=DE,若∠AED=60°,∠ADB=30°,则∠BCF的度数为( ).A.150° B.40° C.80° D.90° ( http: / / www.21cnjy.com )二、填空题4.如图所示,AC=DB,要使△ABC≌△DCB,只需添加条件_________,从而利用“SSS”来证明. ( http: / / www.21cnjy.com )5.如图所示,△ABC中,AB=AC,E,D,F是BC边的四等分点,AE=AF,则图中全等三角形共有_______对. ( http: / / www.21cnjy.com )三、解答题6.小强同学学完三角形全等的判定定理“SS ( http: / / www.21cnjy.com )S”后,自制了一个平分角的仪器,如图所示,AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线,你觉得他说的有道理吗?为什么? ( http: / / www.21cnjy.com )7.如图所示,已知:A,C,F,D四点在同一直线上,AB=DE,BC=EF,AF=DC,求证:AB∥DE. ( http: / / www.21cnjy.com )8.如图所示,AB=AC,AD=AE,BE=CD,求证:∠DAB=∠EAC,∠BMC=∠CNB. ( http: / / www.21cnjy.com )9.如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠A+∠D=180°. ( http: / / www.21cnjy.com )10.如图所示,△ABC是 ( http: / / www.21cnjy.com )不等边三角形,DE=BC,以D,E两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画多少个? ( http: / / www.21cnjy.com )11.(2009年宜宾市)已知:如图所示,在四边形ABCD中,AB=CB,AD=CD,求证:∠C=∠A. ( http: / / www.21cnjy.com )12.如图、所示,AE=AD,AB=AC,BD=CE,求证:∠BEC=∠CDB. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】已知三条边对应相等,利用“SSS”即可证明.
证明:在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
练1.【解析】要证△ADC≌△BCD,只需看这两个三角形的三条边是否分别相等.
证明:∵CD=CD,
在△ADC和△BCD中,
∴△ADC≌△BCD(SSS).
【例2】【解析】∵AD=FC,
∴AD+DC=FC+DC,即AC=FD.
在△ABC和△FED中,
∴△ABC≌△FED(SSS).
练2.【解析】要证△AOC≌△BOD,只需看这两个三角形的三条边是否分别相等.
证明:∵O是是AB、CD的中点,
∴AO=BO,CO=DO.
在△AOC和△BOD中,
∴△AOC≌△BOD.
【例3】【解析】在△ABC与△DCB中,
∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB,∠ACB=∠DBC.
∴∠ABC-∠DBC=∠DCB-∠ACB.
即∠1=∠2.
练3.【解析】AD⊥BC符合要求,理由如下:
∵点D是BC的中点,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.
∴AD⊥BC.
课后小测答案:
一、选择题
1.B
2.D
3.D
二、填空题
4.【解析】两个三角形有公共边BC,所以根据SSS,答案为:AB=DC.
5.【解析】4对.它们是:△ABD≌△ACD,△ABE≌△ACF,△AED≌△AFD,△ABF≌ACE.
三、解答题
6.【解析】有道理,理由如下:
在△ACB与△ACD中,
∴△ACB≌△ACD(SSS).
∴∠BAC=∠DAC,即AE是∠DAB的平分线.
7.【解析】先根据SSS证明两三角形全等,由三角形全等的性质得出:∠A=∠D,即可证明AB∥DE.
证明:∵AF=DC,
∴AF-CF=DC-CF.
∴AC=DF.
在△ABC与△DEF中,
∴△ABC≌△DEF(SSS).
∴∠A=∠D.
∴AB∥DE.
8.【解析】在△ADC与△AEB中,
∴△ADC≌△AEB(SSS).
∴∠DAC=∠EAB.
∴∠DAC-∠BAC=∠EAB-∠BAC.
∴∠DAB=∠EAC.
∵△ADC≌△AEB,
∴∠B=∠C.
∴∠B+∠BAC=∠C+∠BAC.
∴∠BMC=∠CNB.
9.【解析】证明:连接AC,在△ADC与△CBA中,
∴△ADC≌△CBA(SSS),
∴∠ACD=∠CAB,
∴AB∥CD,
∴∠A+∠D=180°.
10.【解析】因为所作三角形的一边DE等于已知△ABC的一边BC,则有下列情况:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
如图(1)中,DE=BC,DM=BA,ME=AC;
如图(2)中,DE=BC,DM=CA,ME=AB;
如图(3)中,DE=BC,DM=BA,ME=AC;
如图(4)中,DE=BC,DM=CA,ME=AB.
故这样的三角形最多可以画出4个.
11.【解析】连接BD,在△ABD和△CBD中,
∴△ABD≌△CBD(SSS).
∴∠C=∠A.
12.【解析】先根据SSS证明△ABD≌△ACE全等,再根据等量代换证出∠CDB=∠BEC.
证明:在△ABD与△ACE中,
∴△ABD≌△ACE(SSS).
∴∠ADB=∠AEC.
∵∠ADB+∠CDB=∠AEC+∠BEC=180°,
∴∠CDB=∠BEC.
二、知识回顾 ▲什么叫全等三角形? 能够重合的两个三角形叫全等三角形 .▲全等三角形的性质:全等三角形的 对应边相等 ,全等三角形的 对应角相等 .▲已知△ABC≌△DEF,找出其中相等的边与角 ( http: / / www.21cnjy.com ) ①AB=DE,②BC=EF,③CA=FD,④∠A=∠D,⑤∠B=∠E,⑥∠C=∠F. 满足这六个条件(三个角和三个边分别相等)可以保证△ABC≌△DEF? 可以
三、新知讲解 1.SSS 三边分别相等 的两个三角形全等(简称SSS).这个定理说明,只要三角形的三边长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有 稳定性 的原理.2.利用SSS证明三角形全等判断两个三角形全等的推理过程,叫做证明三角形全等.如下图,已知:△ABC与△DEF的三条边对应相等,求证:△ABC≌△DEF. ( http: / / www.21cnjy.com )证明:在△ABC与△DEF中, ∴△ABC≌△DEF(SSS).3.利用SSS作一个角等于已知角用直尺和圆规作一个角等于已知角的示意图如图所示,说明的依据是 全等三角形的对应角相等 . ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.利用SSS直接证明三角形全等【例1】如图所示,已知AB=DE,AC=DF,BC=EF,求证:△ABC≌△DEF. ( http: / / www.21cnjy.com )总结:如果两个三角形的三边分别对应相等,则两个三角形全等.其几何语言(证明格式)为: ( http: / / www.21cnjy.com )证明:在△ABC与△DEF中,∴△ABC≌△DEF(SSS).练1如图所示,AD=BC,AC=BD,求证:△ADC≌△BCD. ( http: / / www.21cnjy.com )2.先证明对应边相等,再证全等(利用中点、等量相加等)【例2】如图所示,在△ABC和△FED中,AD=FC,AB=FE,BC=ED,求证:△ABC≌△FED. ( http: / / www.21cnjy.com )总结:利用“SSS”证明两个三角形全等,有如下几种常见类型:(1)有公共边的两个三角形.(2)有公共线段的两个三角形,我们可以用等量相加或相减,推出两边相等.(3)含有中点的两个三角形,如图:AB=AC,D是BC的中点, ( http: / / www.21cnjy.com ),由中点的定义可得:BD=CD.继而可证△ABD≌△ACD.练2如图,已知AC=BD,0是AB、CD的中点,求证△AOC≌△BOD. ( http: / / www.21cnjy.com )3.先利用SSS证明三角形全等,继而证明边(角)相等,或求边(角)【例3】如图所示,AB=DC,AC=DB,求证:∠1=∠2. ( http: / / www.21cnjy.com )总结:要求证在两个不同三角形内的角相等,往往利用全等三角形的性质.当两个角所在的三角形不易证全等时,可以利用等量的和(差)相等,将问题转化.求证不在同一个三角形内的两边相等,同样可以利用全等三角形的性质.练3如图是“人”字形屋梁,AB=AC.现 ( http: / / www.21cnjy.com )在要在水平横梁BC上立一根垂直的支柱支撑屋梁,工人师傅取BC的中点D,然后在A,D之间竖支柱AD.那么这根AD符合“垂直”的要求吗?为什么? ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.如图所示,如果AB=C′A′,BC=A′B′,AC=C′B′,那么( ).A.△ABC≌△A′B′C′ B.△ABC≌△C′A′B′C.△ABC≌△B′C′A′ D.这两个三角形不全等 ( http: / / www.21cnjy.com )2.如图,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( ).A.△ABC≌△DBC B.∠A=∠D C.BC是∠ACD的平分线 D.∠A=∠BCD ( http: / / www.21cnjy.com )3.如图所示,AE=CF,AD=BC,E, ( http: / / www.21cnjy.com )F为BD上的两点,且BF=DE,若∠AED=60°,∠ADB=30°,则∠BCF的度数为( ).A.150° B.40° C.80° D.90° ( http: / / www.21cnjy.com )二、填空题4.如图所示,AC=DB,要使△ABC≌△DCB,只需添加条件_________,从而利用“SSS”来证明. ( http: / / www.21cnjy.com )5.如图所示,△ABC中,AB=AC,E,D,F是BC边的四等分点,AE=AF,则图中全等三角形共有_______对. ( http: / / www.21cnjy.com )三、解答题6.小强同学学完三角形全等的判定定理“SS ( http: / / www.21cnjy.com )S”后,自制了一个平分角的仪器,如图所示,AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线,你觉得他说的有道理吗?为什么? ( http: / / www.21cnjy.com )7.如图所示,已知:A,C,F,D四点在同一直线上,AB=DE,BC=EF,AF=DC,求证:AB∥DE. ( http: / / www.21cnjy.com )8.如图所示,AB=AC,AD=AE,BE=CD,求证:∠DAB=∠EAC,∠BMC=∠CNB. ( http: / / www.21cnjy.com )9.如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠A+∠D=180°. ( http: / / www.21cnjy.com )10.如图所示,△ABC是 ( http: / / www.21cnjy.com )不等边三角形,DE=BC,以D,E两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画多少个? ( http: / / www.21cnjy.com )11.(2009年宜宾市)已知:如图所示,在四边形ABCD中,AB=CB,AD=CD,求证:∠C=∠A. ( http: / / www.21cnjy.com )12.如图、所示,AE=AD,AB=AC,BD=CE,求证:∠BEC=∠CDB. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】已知三条边对应相等,利用“SSS”即可证明.
证明:在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
练1.【解析】要证△ADC≌△BCD,只需看这两个三角形的三条边是否分别相等.
证明:∵CD=CD,
在△ADC和△BCD中,
∴△ADC≌△BCD(SSS).
【例2】【解析】∵AD=FC,
∴AD+DC=FC+DC,即AC=FD.
在△ABC和△FED中,
∴△ABC≌△FED(SSS).
练2.【解析】要证△AOC≌△BOD,只需看这两个三角形的三条边是否分别相等.
证明:∵O是是AB、CD的中点,
∴AO=BO,CO=DO.
在△AOC和△BOD中,
∴△AOC≌△BOD.
【例3】【解析】在△ABC与△DCB中,
∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB,∠ACB=∠DBC.
∴∠ABC-∠DBC=∠DCB-∠ACB.
即∠1=∠2.
练3.【解析】AD⊥BC符合要求,理由如下:
∵点D是BC的中点,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.
∴AD⊥BC.
课后小测答案:
一、选择题
1.B
2.D
3.D
二、填空题
4.【解析】两个三角形有公共边BC,所以根据SSS,答案为:AB=DC.
5.【解析】4对.它们是:△ABD≌△ACD,△ABE≌△ACF,△AED≌△AFD,△ABF≌ACE.
三、解答题
6.【解析】有道理,理由如下:
在△ACB与△ACD中,
∴△ACB≌△ACD(SSS).
∴∠BAC=∠DAC,即AE是∠DAB的平分线.
7.【解析】先根据SSS证明两三角形全等,由三角形全等的性质得出:∠A=∠D,即可证明AB∥DE.
证明:∵AF=DC,
∴AF-CF=DC-CF.
∴AC=DF.
在△ABC与△DEF中,
∴△ABC≌△DEF(SSS).
∴∠A=∠D.
∴AB∥DE.
8.【解析】在△ADC与△AEB中,
∴△ADC≌△AEB(SSS).
∴∠DAC=∠EAB.
∴∠DAC-∠BAC=∠EAB-∠BAC.
∴∠DAB=∠EAC.
∵△ADC≌△AEB,
∴∠B=∠C.
∴∠B+∠BAC=∠C+∠BAC.
∴∠BMC=∠CNB.
9.【解析】证明:连接AC,在△ADC与△CBA中,
∴△ADC≌△CBA(SSS),
∴∠ACD=∠CAB,
∴AB∥CD,
∴∠A+∠D=180°.
10.【解析】因为所作三角形的一边DE等于已知△ABC的一边BC,则有下列情况:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
如图(1)中,DE=BC,DM=BA,ME=AC;
如图(2)中,DE=BC,DM=CA,ME=AB;
如图(3)中,DE=BC,DM=BA,ME=AC;
如图(4)中,DE=BC,DM=CA,ME=AB.
故这样的三角形最多可以画出4个.
11.【解析】连接BD,在△ABD和△CBD中,
∴△ABD≌△CBD(SSS).
∴∠C=∠A.
12.【解析】先根据SSS证明△ABD≌△ACE全等,再根据等量代换证出∠CDB=∠BEC.
证明:在△ABD与△ACE中,
∴△ABD≌△ACE(SSS).
∴∠ADB=∠AEC.
∵∠ADB+∠CDB=∠AEC+∠BEC=180°,
∴∠CDB=∠BEC.
