【多媒体导学案】人教版数学八年级上册第12章第8课时角平分线的性质(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第8课时角平分线的性质(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 285.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 19:41:24 | ||
图片预览



文档简介
一、学习目标 了解角平分线的定义,会用尺规作一个角的平分线;掌握角平分线的性质和判定;会利用角平分线的性质与判定证明简单的线段相等、角相等问题,并能解决简单的实际问题.
二、知识回顾 1.从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线;2.直线外一点到这条直线的垂线段的长度叫做点到直线的距离;3.如图,已知AB=AD,BC=DC,利用全等的方法证明AC是∠DAB的平分线. ( http: / / www.21cnjy.com )证明:∵AB=AD,BC=DC(已知),AC=AC(公共边),∴△ABC≌△ADC,∴∠BAC=∠DAC,∴AC是∠DAB的平分线.
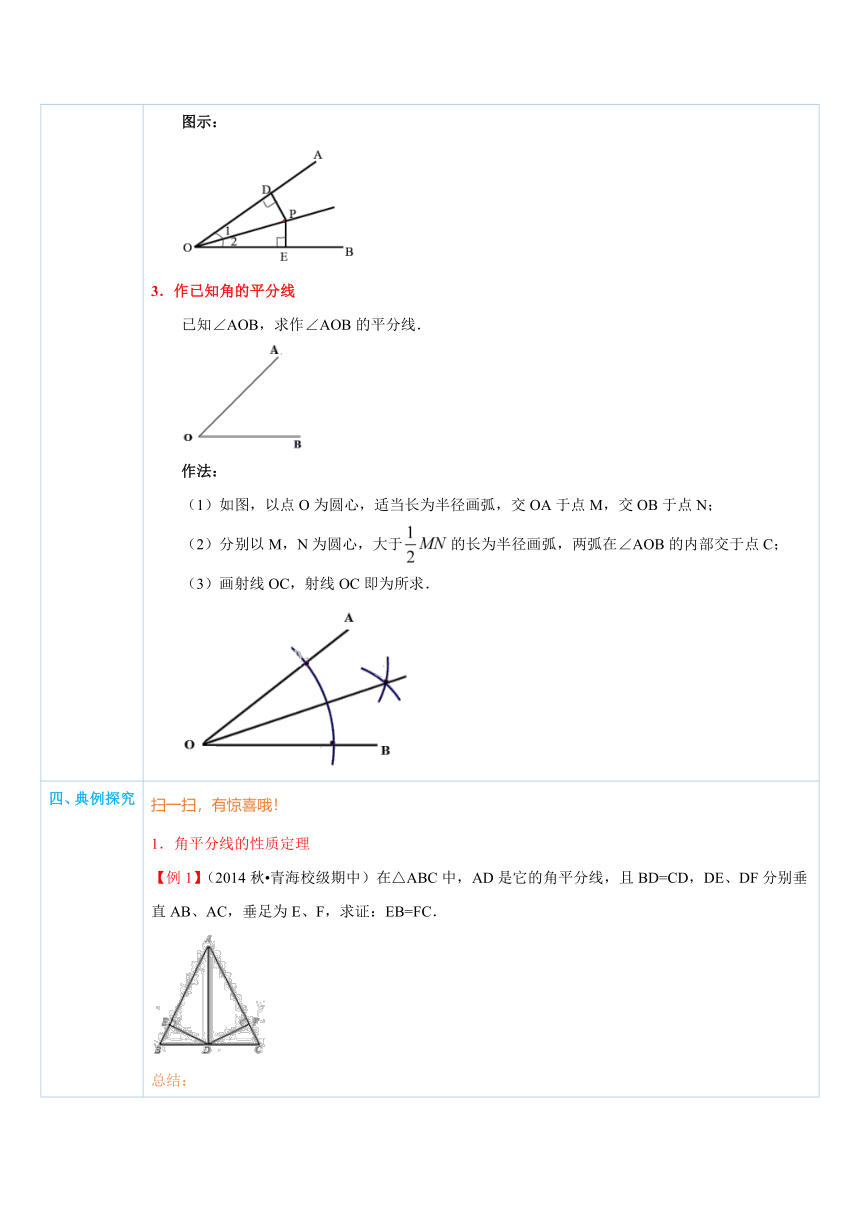
三、新知讲解 1.角平分线的性质定理文字描述:在角平分线上的点到角的两边的距离相等.符号语言:∵∠1=∠2,PD⊥OA,PE⊥OB,∴PD=PE.图示: ( http: / / www.21cnjy.com )2.角平分线性质定理的逆定理(角平分线的判定定理)文字描述:角的内部到角的两边的距离相等的点在角的平分线上.符号语言:∵PD⊥OA,PE⊥OB,PD=PE,∴点P在∠AOB的平分线上(OP是∠AOB的平分线).图示: ( http: / / www.21cnjy.com )3.作已知角的平分线已知∠AOB,求作∠AOB的平分线.作法:(1)如图,以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;(2)分别以M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部交于点C;(3)画射线OC,射线OC即为所求.
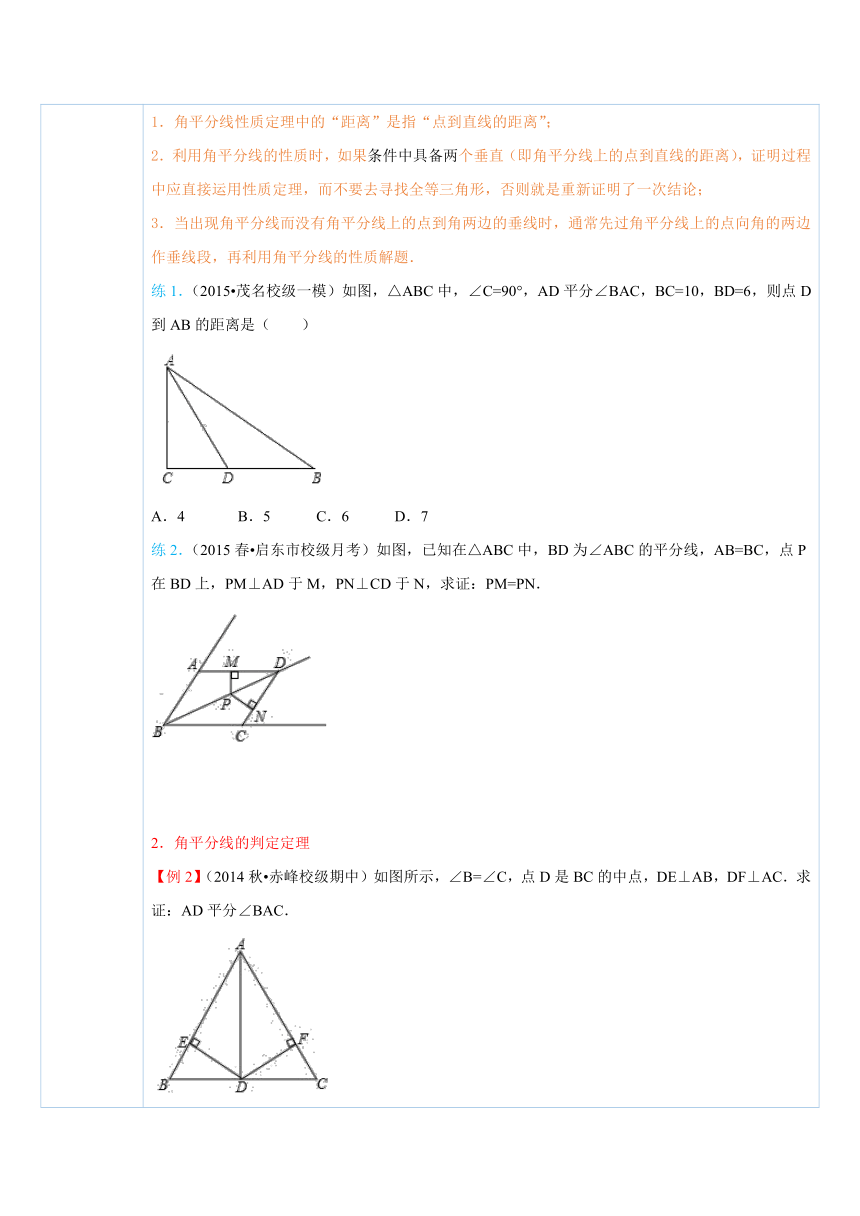
四、典例探究 ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.角平分线的性质定理【例1】(2014秋 青海校级期中)在△ ( http: / / www.21cnjy.com )ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直AB、AC,垂足为E、F,求证:EB=FC. ( http: / / www.21cnjy.com )总结:1.角平分线性质定理中的“距离”是指“点到直线的距离”;2.利用角平分线的性质时,如果条件中具备两 ( http: / / www.21cnjy.com )个垂直(即角平分线上的点到直线的距离),证明过程中应直接运用性质定理,而不要去寻找全等三角形,否则就是重新证明了一次结论;3.当出现角平分线而没有角平分线上的点到角两边的垂线时,通常先过角平分线上的点向角的两边作垂线段,再利用角平分线的性质解题.练1.(2015 茂名校级一模)如图,△ABC中,∠C=90°,AD平分∠BAC,BC=10,BD=6,则点D到AB的距离是( ) ( http: / / www.21cnjy.com )A.4 B.5 C.6 D.7练2.(2015春 启东市校级月考)如图, ( http: / / www.21cnjy.com )已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN. ( http: / / www.21cnjy.com )2.角平分线的判定定理【例2】(2014秋 赤峰校级期中)如图所示,∠B=∠C,点D是BC的中点,DE⊥AB,DF⊥AC.求证:AD平分∠BAC. ( http: / / www.21cnjy.com )总结:1.角平分线的性质定理是证 ( http: / / www.21cnjy.com )明线段相等的一种方法,条件是已知角的平分线,而角平分线的判定定理是证明角相等的一种方法,条件是到已知角的两边的距离相等;2.证明某点在角平分线上的常用方法是证 ( http: / / www.21cnjy.com )明这个点到角的两边的距离相等,这样就把证明“点在线上”的问题转化为“线段相等”的问题,体现了“化难为易,化陌生为熟悉”的转化思想.练3.(2013秋 兴化市校级期中)如图,PB,PC分别是△ABC的外角平分线且相交于P.求证:P在∠A的平分线上. ( http: / / www.21cnjy.com )3.角平分线性质的实际应用【例3】有三条交叉公路如图所示,要 ( http: / / www.21cnjy.com )在三角形区域内建一个加油站,使加油站P到三条公路的距离相等,应建在什么位置?请用尺规作图标出加油站P的位置. ( http: / / www.21cnjy.com )总结:因为三角形的三条角平分线相交于一点,又角平分线的点到角两边的距离相等,所以三角形角平分线的交点到三边的距离相等.要画三角形三条角平分线的交点,只需要画三角形的两条角平分线即可.注意:三角形外角平分线上的点到外角 ( http: / / www.21cnjy.com )两边的距离也相等,所以三角形外还有3个点到三角形三边所在的直线的距离相等,它们都是两条外角平分线和一条内角平分线的交点.练4.如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( ) ( http: / / www.21cnjy.com )A.一处 B.二处 C.三处 D.四处
五、课后小测 一、选择题1.(2014秋 荣昌县期末)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( ) ( http: / / www.21cnjy.com )A.1 B.2 C.3 D.42.(2014春 栖霞市期末)在Rt△ABC ( http: / / www.21cnjy.com )中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于( ) ( http: / / www.21cnjy.com )A.3.8cm B.7.6cm C.11.4cm D.11.2cm3.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在( ) ( http: / / www.21cnjy.com )A.三角形两边高线的交点处 B.三角形两边中线的交点处C.∠α的平分线上 D.∠α和∠β的平分线的交点处二、填空题4.(2013秋 太康县期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,则点D到AB的距离是 . ( http: / / www.21cnjy.com )5.(2014秋 惠安县期 ( http: / / www.21cnjy.com )末)如图,OC平分∠AOB,点P是OC上一点,PM⊥OB于点M,点N是射线OA上的一个动点,若PM=5,则PN的最小值为 . ( http: / / www.21cnjy.com )6.(2014秋 临沭县 ( http: / / www.21cnjy.com )校级月考)如图,△ABC的三边AB、BC、CA的长分别是20、30、40、其中三条角平分线交于点0,则S△ABO:S△BCO:S△CAO等于 . ( http: / / www.21cnjy.com )三、解答题7.(2014秋 利津县校级月考)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB. ( http: / / www.21cnjy.com )8.(2013秋 黄山校级期末)如图, ( http: / / www.21cnjy.com )在Rt△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E.若△DBE的周长为15cm,求AB的长. ( http: / / www.21cnjy.com )9.(2014秋 陇西县期末)如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足为C,D.求证:(1)OC=OD;(2)DF=CF. ( http: / / www.21cnjy.com )10.(2013秋 临沭县期末)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线. ( http: / / www.21cnjy.com )11.(2014秋 门头沟区期末)已知 ( http: / / www.21cnjy.com ):在Rt△ABC中,∠C=90°.请在线段BC上作一点D,使点D到边AC、AB的距离相等(要求:尺规作图,不写作法,保留作图痕迹).12.(2014秋 厦门期中)如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;(2)求证:点P在∠HAC的平分线上. ( http: / / www.21cnjy.com )13.(2013秋 淮北期末)已知点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC(1)如图1,若点O在BC上,求证:AB=AC.(2)如图2,若点O在△ABC内部,求证:AB=AC.(3)猜想,若O点在△ABC的外部,AB=AC成立吗? ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】依题意知DE⊥AB ( http: / / www.21cnjy.com ),DF⊥AC,AD平分∠BAC,由角平分线性质得DE=DF,已知BD=DC,利用“HL”证明△BDE≌△CDF即可.
证明:∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF.
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴EB=FC.
点评:本题考查了角平分线性质的运用,三角形全等的判定和性质.关键是寻找证明三角形全等的条件.
练1.【解析】由角平分线的性质可得点D到AB的距离等于CD,根据已知求得CD即可.
解:∵∠C=90°,AD平分∠BAC,
∴点D到AB的距离等于CD,
∵BC=10,BD=6,
∴CD=BC﹣BD=10﹣6=4,
∴点D到AB的距离是4.
故选A.
点评:此题主要考查角平分线的性质:角的平分线上的点到角的两边的距离相等.
练2.【解析】根据角平分线的定义可得∠A ( http: / / www.21cnjy.com )BD=∠CBD,然后利用“边角边”证明△ABD和△CBD全等,根据全等三角形对应角相等可得∠ADB=∠CDB,然后根据角平分线上的点到角的两边的距离相等证明即可.
证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,确定出全等三角形并得到∠ADB=∠CDB是解题的关键.
【例2】【解析】由条件可证明△BDE≌△CDF,可得到DE=DF,可证得结论.
证明:∵D是BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC.
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴DE=DF,
∴D在∠BAC的平分线上,
即AD平分∠BAC.
点评:本题主要考查角平分线的判定,掌握在角的内部到角两边的距离相等的点在角的平分线上是解题的关键.
练3.【解析】过P点作PE,PH,P ( http: / / www.21cnjy.com )G分别垂直AB,BC,AC,要证P在∠A的平分线上,则需证PE=PG,利用角的平分线上的点到角的两边的距离相等就可证明PE=PG.
证明:过P点作PE,PH,PG分别垂直AB,BC,AC.
( http: / / www.21cnjy.com )
∵PB,PC分别是△ABC的外角平分线,
∴PE=PH,PH=PG,
∴PE=PG.
∴P点在∠A的平分线上.
点评:本题主要考查角平分线性质的逆定理.准确作出辅助线是解决本题的关键.
【例3】【解析】分别作∠ABC与∠ACB的平分线,两条角平分线交于点P,则点P即为所求点.
解:∵加油站P到三条公路的距离相等,
∴P点是△ABC的内心,
∴加油站P应该建在三角形内角平分线的交点处.
如图所示:
( http: / / www.21cnjy.com )
①以点B为圆心,以任意长为半径画圆,分别交AB、BC于点D、E;
②分别以点DE为圆心,以大于DE为半径画圆,两圆相交于点F.连接BF,则BF即为∠ABC的平分线;
同理作出∠ACB的平分线,两条角平分线交于点P,则点P即为所求点.
点评:熟知角平分线上的点到角两边距离相等的性质是解答此题的关键.
练4.【解析】到三条相互交叉的公路距离 ( http: / / www.21cnjy.com )相等的地点应是三条角平分线的交点.把三条公路的中心部位看作三角形,那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求.
解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三个外角两两平分线的交点,共三处.
( http: / / www.21cnjy.com )
故选D.
点评:此题考查了角平分线的性质.此题难度不大,注意掌握角平分线的定理的应用是关键.
课后小测答案:
一、选择题
1.【解析】∵垂线段最短,
∴当PQ⊥OM时,PQ有最小值,
又∵OP平分∠MON,PA⊥ON,
∴PQ=PA=2,
故选B.
2.【解析】∵∠C=90°,∠CAB=60°,
∴∠B=30°,在Rt△BDE中,BD=2DE=7.6,
又∵AD平分∠CAB,
∴DC=DE=3.8,
∴BC=BD+DC=7.6+3.8=11.4.
故选C.
3.【解析】∵如图,要建一超市到a、b、c三条公路的距离相等,
( http: / / www.21cnjy.com )
∴该超市是△ABC的内心,
∴超市应该建在∠α和∠β的平分线的交点处.
故选D.
二、填空题
4.【解析】∵BC=6,BD=4
∴CD=2
∵∠C=90°,AD平分∠CAB
∴点D到AB的距离=CD=2.
故填2.
5.【解析】当PN⊥OA时,PN的值最小,
∵OC平分∠AOB,PM⊥OB,
∴PM=PN,
∵PM=5,
∴PN的最小值为5.
故答案为:5.
6.【解析】过O分别作OE⊥CB,FO⊥AB,OD⊥AC,
( http: / / www.21cnjy.com )
∵BO是∠ABC平分线,
∴EO=FO,
∵CO是∠ACB平分线,
∴EO=DO,
∴EO=DO=FO,
∵S△ABO=AB FO,S△BCO=CB EO,S△CAO=AC DO,
∴S△ABO:S△BCO:S△CAO=20:30:40=2:3:4.
故答案为:2:3:4.
三、解答题
7.【解析】∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
8.【解析】∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴△ACD≌△AED,
∴CD=DE,AE=AC,
∴△DBE的周长=BD+EB+DE=BD+EB+CD=BC+EB=AC+EB=AE+EB=AB=15cm,
∴AB=15cm.
9.【解析】证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=DE,∠ECO=∠EDO=90°,
在Rt△COE和Rt△DOE中,
,
∴Rt△COE≌Rt△DOE(HL),
∴CO=DO;
(2)∵EO平分∠AOB,
∴∠AOE=∠BOE,
在△COF和△DOF中,
,
∴△COF≌△DOF(SAS),
∴FC=FD.
10.【解析】证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△DCF是直角三角形.
,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是角平分线.
11.【解析】如图所示:点D为所求;
( http: / / www.21cnjy.com )
12.【解析】(1)过P作PF⊥BE于F,如图,
( http: / / www.21cnjy.com )
∵BP平分∠ABC,PH⊥BA于H,PF⊥BE于F,
∴PH=PF=5cm,
∴点P到直线BC的距离为5cm;
(2)证明:∵CP平分∠ACE,PD⊥AC于D,PF⊥BE于F,
∴PF=PD,
∴PD=PH,
∴AP平分∠HAD.
13.【解析】证明:(1)过点O作OD⊥AB于D,作OE⊥AC于E,
( http: / / www.21cnjy.com )
则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵,
∴Rt△BOD≌Rt△COE(HL),
∴∠B=∠C,
∴AB=AC;
(2)过点O作OD⊥AB于D,OE⊥AC于E,
( http: / / www.21cnjy.com )
则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵,
∴Rt△BOD≌Rt△COE(HL),
∴∠DBO=∠ECO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)不一定成立.
证明:如图3,过点O作OD⊥AB于D,作OE⊥AC的延长线于点E,
( http: / / www.21cnjy.com )
则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵,
∴Rt△BOD≌Rt△COE(HL),
∴∠DBO=∠ECO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠DBC=∠ECB,
∴∠ABC=∠ACB,
∴AB=AC.
如图4,
( http: / / www.21cnjy.com )
可知AB≠AC.
二、知识回顾 1.从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线;2.直线外一点到这条直线的垂线段的长度叫做点到直线的距离;3.如图,已知AB=AD,BC=DC,利用全等的方法证明AC是∠DAB的平分线. ( http: / / www.21cnjy.com )证明:∵AB=AD,BC=DC(已知),AC=AC(公共边),∴△ABC≌△ADC,∴∠BAC=∠DAC,∴AC是∠DAB的平分线.
三、新知讲解 1.角平分线的性质定理文字描述:在角平分线上的点到角的两边的距离相等.符号语言:∵∠1=∠2,PD⊥OA,PE⊥OB,∴PD=PE.图示: ( http: / / www.21cnjy.com )2.角平分线性质定理的逆定理(角平分线的判定定理)文字描述:角的内部到角的两边的距离相等的点在角的平分线上.符号语言:∵PD⊥OA,PE⊥OB,PD=PE,∴点P在∠AOB的平分线上(OP是∠AOB的平分线).图示: ( http: / / www.21cnjy.com )3.作已知角的平分线已知∠AOB,求作∠AOB的平分线.作法:(1)如图,以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;(2)分别以M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部交于点C;(3)画射线OC,射线OC即为所求.
四、典例探究 ( http: / / www.21cnjy.com ) 扫一扫,有惊喜哦!1.角平分线的性质定理【例1】(2014秋 青海校级期中)在△ ( http: / / www.21cnjy.com )ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直AB、AC,垂足为E、F,求证:EB=FC. ( http: / / www.21cnjy.com )总结:1.角平分线性质定理中的“距离”是指“点到直线的距离”;2.利用角平分线的性质时,如果条件中具备两 ( http: / / www.21cnjy.com )个垂直(即角平分线上的点到直线的距离),证明过程中应直接运用性质定理,而不要去寻找全等三角形,否则就是重新证明了一次结论;3.当出现角平分线而没有角平分线上的点到角两边的垂线时,通常先过角平分线上的点向角的两边作垂线段,再利用角平分线的性质解题.练1.(2015 茂名校级一模)如图,△ABC中,∠C=90°,AD平分∠BAC,BC=10,BD=6,则点D到AB的距离是( ) ( http: / / www.21cnjy.com )A.4 B.5 C.6 D.7练2.(2015春 启东市校级月考)如图, ( http: / / www.21cnjy.com )已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN. ( http: / / www.21cnjy.com )2.角平分线的判定定理【例2】(2014秋 赤峰校级期中)如图所示,∠B=∠C,点D是BC的中点,DE⊥AB,DF⊥AC.求证:AD平分∠BAC. ( http: / / www.21cnjy.com )总结:1.角平分线的性质定理是证 ( http: / / www.21cnjy.com )明线段相等的一种方法,条件是已知角的平分线,而角平分线的判定定理是证明角相等的一种方法,条件是到已知角的两边的距离相等;2.证明某点在角平分线上的常用方法是证 ( http: / / www.21cnjy.com )明这个点到角的两边的距离相等,这样就把证明“点在线上”的问题转化为“线段相等”的问题,体现了“化难为易,化陌生为熟悉”的转化思想.练3.(2013秋 兴化市校级期中)如图,PB,PC分别是△ABC的外角平分线且相交于P.求证:P在∠A的平分线上. ( http: / / www.21cnjy.com )3.角平分线性质的实际应用【例3】有三条交叉公路如图所示,要 ( http: / / www.21cnjy.com )在三角形区域内建一个加油站,使加油站P到三条公路的距离相等,应建在什么位置?请用尺规作图标出加油站P的位置. ( http: / / www.21cnjy.com )总结:因为三角形的三条角平分线相交于一点,又角平分线的点到角两边的距离相等,所以三角形角平分线的交点到三边的距离相等.要画三角形三条角平分线的交点,只需要画三角形的两条角平分线即可.注意:三角形外角平分线上的点到外角 ( http: / / www.21cnjy.com )两边的距离也相等,所以三角形外还有3个点到三角形三边所在的直线的距离相等,它们都是两条外角平分线和一条内角平分线的交点.练4.如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( ) ( http: / / www.21cnjy.com )A.一处 B.二处 C.三处 D.四处
五、课后小测 一、选择题1.(2014秋 荣昌县期末)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( ) ( http: / / www.21cnjy.com )A.1 B.2 C.3 D.42.(2014春 栖霞市期末)在Rt△ABC ( http: / / www.21cnjy.com )中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于( ) ( http: / / www.21cnjy.com )A.3.8cm B.7.6cm C.11.4cm D.11.2cm3.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在( ) ( http: / / www.21cnjy.com )A.三角形两边高线的交点处 B.三角形两边中线的交点处C.∠α的平分线上 D.∠α和∠β的平分线的交点处二、填空题4.(2013秋 太康县期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,则点D到AB的距离是 . ( http: / / www.21cnjy.com )5.(2014秋 惠安县期 ( http: / / www.21cnjy.com )末)如图,OC平分∠AOB,点P是OC上一点,PM⊥OB于点M,点N是射线OA上的一个动点,若PM=5,则PN的最小值为 . ( http: / / www.21cnjy.com )6.(2014秋 临沭县 ( http: / / www.21cnjy.com )校级月考)如图,△ABC的三边AB、BC、CA的长分别是20、30、40、其中三条角平分线交于点0,则S△ABO:S△BCO:S△CAO等于 . ( http: / / www.21cnjy.com )三、解答题7.(2014秋 利津县校级月考)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB. ( http: / / www.21cnjy.com )8.(2013秋 黄山校级期末)如图, ( http: / / www.21cnjy.com )在Rt△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E.若△DBE的周长为15cm,求AB的长. ( http: / / www.21cnjy.com )9.(2014秋 陇西县期末)如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足为C,D.求证:(1)OC=OD;(2)DF=CF. ( http: / / www.21cnjy.com )10.(2013秋 临沭县期末)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线. ( http: / / www.21cnjy.com )11.(2014秋 门头沟区期末)已知 ( http: / / www.21cnjy.com ):在Rt△ABC中,∠C=90°.请在线段BC上作一点D,使点D到边AC、AB的距离相等(要求:尺规作图,不写作法,保留作图痕迹).12.(2014秋 厦门期中)如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;(2)求证:点P在∠HAC的平分线上. ( http: / / www.21cnjy.com )13.(2013秋 淮北期末)已知点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC(1)如图1,若点O在BC上,求证:AB=AC.(2)如图2,若点O在△ABC内部,求证:AB=AC.(3)猜想,若O点在△ABC的外部,AB=AC成立吗? ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】依题意知DE⊥AB ( http: / / www.21cnjy.com ),DF⊥AC,AD平分∠BAC,由角平分线性质得DE=DF,已知BD=DC,利用“HL”证明△BDE≌△CDF即可.
证明:∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF.
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴EB=FC.
点评:本题考查了角平分线性质的运用,三角形全等的判定和性质.关键是寻找证明三角形全等的条件.
练1.【解析】由角平分线的性质可得点D到AB的距离等于CD,根据已知求得CD即可.
解:∵∠C=90°,AD平分∠BAC,
∴点D到AB的距离等于CD,
∵BC=10,BD=6,
∴CD=BC﹣BD=10﹣6=4,
∴点D到AB的距离是4.
故选A.
点评:此题主要考查角平分线的性质:角的平分线上的点到角的两边的距离相等.
练2.【解析】根据角平分线的定义可得∠A ( http: / / www.21cnjy.com )BD=∠CBD,然后利用“边角边”证明△ABD和△CBD全等,根据全等三角形对应角相等可得∠ADB=∠CDB,然后根据角平分线上的点到角的两边的距离相等证明即可.
证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,确定出全等三角形并得到∠ADB=∠CDB是解题的关键.
【例2】【解析】由条件可证明△BDE≌△CDF,可得到DE=DF,可证得结论.
证明:∵D是BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC.
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴DE=DF,
∴D在∠BAC的平分线上,
即AD平分∠BAC.
点评:本题主要考查角平分线的判定,掌握在角的内部到角两边的距离相等的点在角的平分线上是解题的关键.
练3.【解析】过P点作PE,PH,P ( http: / / www.21cnjy.com )G分别垂直AB,BC,AC,要证P在∠A的平分线上,则需证PE=PG,利用角的平分线上的点到角的两边的距离相等就可证明PE=PG.
证明:过P点作PE,PH,PG分别垂直AB,BC,AC.
( http: / / www.21cnjy.com )
∵PB,PC分别是△ABC的外角平分线,
∴PE=PH,PH=PG,
∴PE=PG.
∴P点在∠A的平分线上.
点评:本题主要考查角平分线性质的逆定理.准确作出辅助线是解决本题的关键.
【例3】【解析】分别作∠ABC与∠ACB的平分线,两条角平分线交于点P,则点P即为所求点.
解:∵加油站P到三条公路的距离相等,
∴P点是△ABC的内心,
∴加油站P应该建在三角形内角平分线的交点处.
如图所示:
( http: / / www.21cnjy.com )
①以点B为圆心,以任意长为半径画圆,分别交AB、BC于点D、E;
②分别以点DE为圆心,以大于DE为半径画圆,两圆相交于点F.连接BF,则BF即为∠ABC的平分线;
同理作出∠ACB的平分线,两条角平分线交于点P,则点P即为所求点.
点评:熟知角平分线上的点到角两边距离相等的性质是解答此题的关键.
练4.【解析】到三条相互交叉的公路距离 ( http: / / www.21cnjy.com )相等的地点应是三条角平分线的交点.把三条公路的中心部位看作三角形,那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求.
解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三个外角两两平分线的交点,共三处.
( http: / / www.21cnjy.com )
故选D.
点评:此题考查了角平分线的性质.此题难度不大,注意掌握角平分线的定理的应用是关键.
课后小测答案:
一、选择题
1.【解析】∵垂线段最短,
∴当PQ⊥OM时,PQ有最小值,
又∵OP平分∠MON,PA⊥ON,
∴PQ=PA=2,
故选B.
2.【解析】∵∠C=90°,∠CAB=60°,
∴∠B=30°,在Rt△BDE中,BD=2DE=7.6,
又∵AD平分∠CAB,
∴DC=DE=3.8,
∴BC=BD+DC=7.6+3.8=11.4.
故选C.
3.【解析】∵如图,要建一超市到a、b、c三条公路的距离相等,
( http: / / www.21cnjy.com )
∴该超市是△ABC的内心,
∴超市应该建在∠α和∠β的平分线的交点处.
故选D.
二、填空题
4.【解析】∵BC=6,BD=4
∴CD=2
∵∠C=90°,AD平分∠CAB
∴点D到AB的距离=CD=2.
故填2.
5.【解析】当PN⊥OA时,PN的值最小,
∵OC平分∠AOB,PM⊥OB,
∴PM=PN,
∵PM=5,
∴PN的最小值为5.
故答案为:5.
6.【解析】过O分别作OE⊥CB,FO⊥AB,OD⊥AC,
( http: / / www.21cnjy.com )
∵BO是∠ABC平分线,
∴EO=FO,
∵CO是∠ACB平分线,
∴EO=DO,
∴EO=DO=FO,
∵S△ABO=AB FO,S△BCO=CB EO,S△CAO=AC DO,
∴S△ABO:S△BCO:S△CAO=20:30:40=2:3:4.
故答案为:2:3:4.
三、解答题
7.【解析】∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
8.【解析】∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴△ACD≌△AED,
∴CD=DE,AE=AC,
∴△DBE的周长=BD+EB+DE=BD+EB+CD=BC+EB=AC+EB=AE+EB=AB=15cm,
∴AB=15cm.
9.【解析】证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=DE,∠ECO=∠EDO=90°,
在Rt△COE和Rt△DOE中,
,
∴Rt△COE≌Rt△DOE(HL),
∴CO=DO;
(2)∵EO平分∠AOB,
∴∠AOE=∠BOE,
在△COF和△DOF中,
,
∴△COF≌△DOF(SAS),
∴FC=FD.
10.【解析】证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△DCF是直角三角形.
,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是角平分线.
11.【解析】如图所示:点D为所求;
( http: / / www.21cnjy.com )
12.【解析】(1)过P作PF⊥BE于F,如图,
( http: / / www.21cnjy.com )
∵BP平分∠ABC,PH⊥BA于H,PF⊥BE于F,
∴PH=PF=5cm,
∴点P到直线BC的距离为5cm;
(2)证明:∵CP平分∠ACE,PD⊥AC于D,PF⊥BE于F,
∴PF=PD,
∴PD=PH,
∴AP平分∠HAD.
13.【解析】证明:(1)过点O作OD⊥AB于D,作OE⊥AC于E,
( http: / / www.21cnjy.com )
则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵,
∴Rt△BOD≌Rt△COE(HL),
∴∠B=∠C,
∴AB=AC;
(2)过点O作OD⊥AB于D,OE⊥AC于E,
( http: / / www.21cnjy.com )
则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵,
∴Rt△BOD≌Rt△COE(HL),
∴∠DBO=∠ECO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)不一定成立.
证明:如图3,过点O作OD⊥AB于D,作OE⊥AC的延长线于点E,
( http: / / www.21cnjy.com )
则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵,
∴Rt△BOD≌Rt△COE(HL),
∴∠DBO=∠ECO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠DBC=∠ECB,
∴∠ABC=∠ACB,
∴AB=AC.
如图4,
( http: / / www.21cnjy.com )
可知AB≠AC.
