【多媒体导学案】人教版数学八年级上册第12章第3课时全等三角形的判定(SAS)(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第3课时全等三角形的判定(SAS)(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 19:36:06 | ||
图片预览


文档简介
一、学习目标 理解全等三角形的判定方法SAS;能运用SAS判定两个三角形全等;经理探索SAS判定两个三角形全等的过程,体会数学知识来源生活,又应用于生活.
二、知识回顾 1.什么是全等三角形?全等三角形的性质有哪些?能够完全重合的三角形叫做全等三角形.全等三角形的性质:全等三角形的对应边相等 ( http: / / www.21cnjy.com );全等三角形的对应角相等;全等三角形对应边上的中线、高相等,对应角的平分线相等;全等三角形的周长面积也相等.2.上一课学习的三角形全等的判定方法是什么?三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
三、新知讲解 1.边角边定理三角形全等判定方法2:两边和它们的夹角分别相等的两个三角形全等.(简称SAS)符号语言:在△ABC与△DEF中,∴△ABC≌△DEF(SAS).图示: ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )2.探索边边角两边及其一边所对的角分别相等,两个三角形不一定全等.
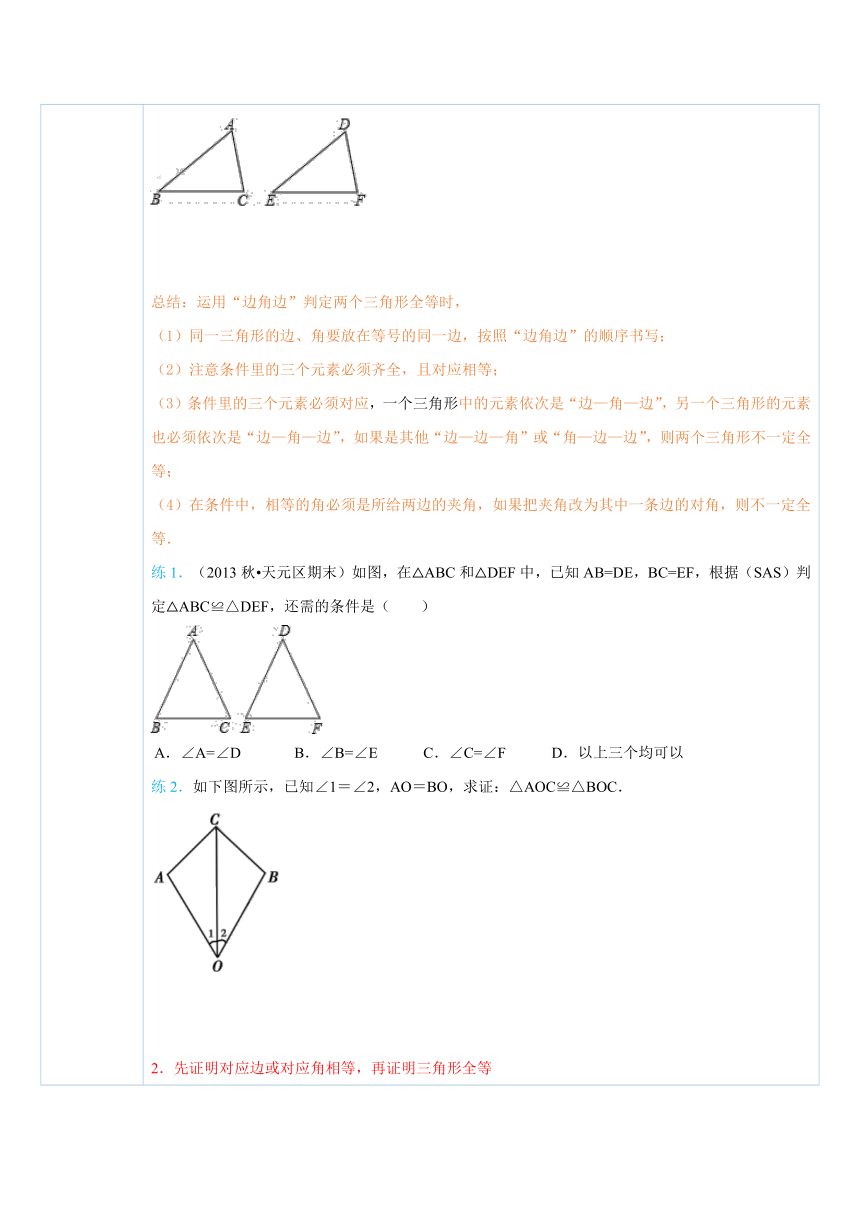
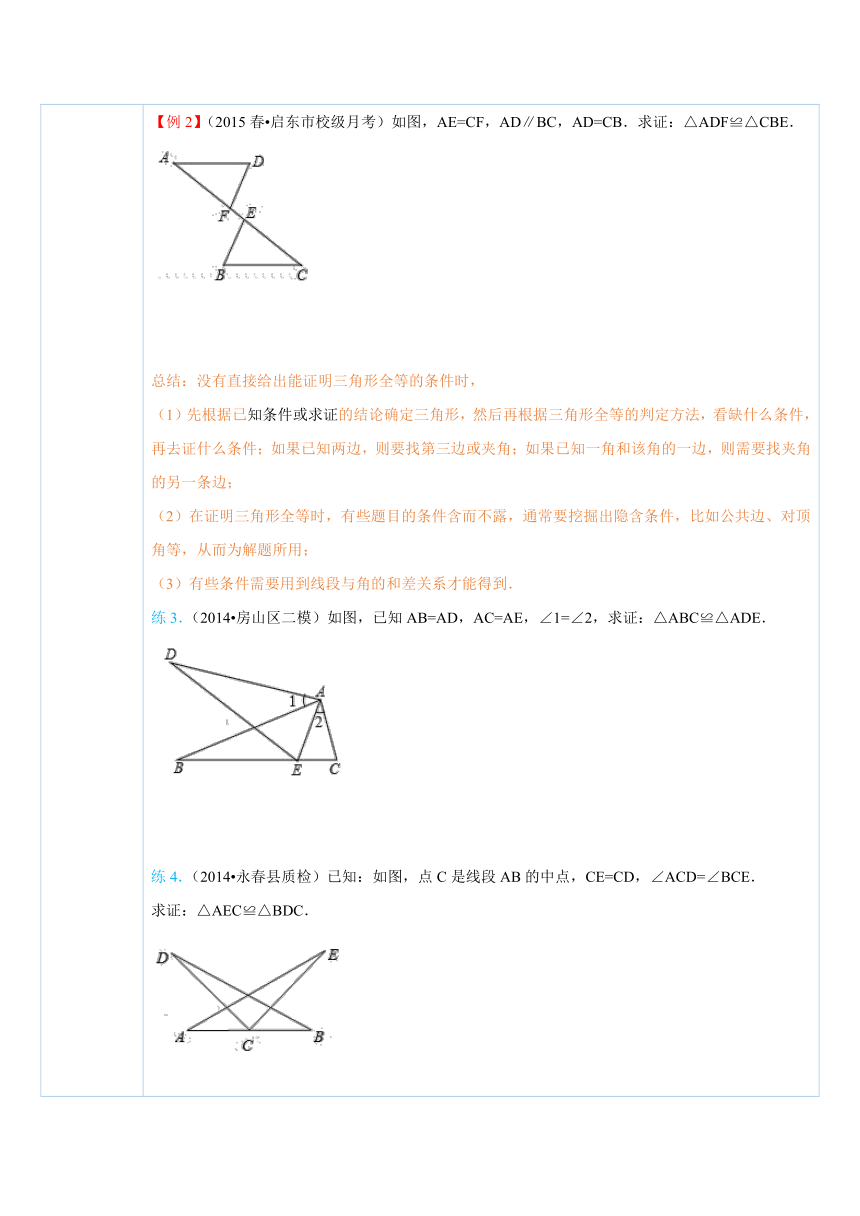
四、典例探究 扫一扫,有惊喜哦!1.利用SAS直接证明三角形全等【例1】如图所示,△ABC,△DEF均为锐角三角形,AB=DE,AC=DF,∠A=∠D.求证:△ABC≌△DEF. ( http: / / www.21cnjy.com )总结:运用“边角边”判定两个三角形全等时,(1)同一三角形的边、角要放在等号的同一边,按照“边角边”的顺序书写;(2)注意条件里的三个元素必须齐全,且对应相等;(3)条件里的三个元素必须对应,一个三角形 ( http: / / www.21cnjy.com )中的元素依次是“边—角—边”,另一个三角形的元素也必须依次是“边—角—边”,如果是其他“边—边—角”或“角—边—边”,则两个三角形不一定全等;(4)在条件中,相等的角必须是所给两边的夹角,如果把夹角改为其中一条边的对角,则不一定全等.练1.(2013秋 天元区期末)如图,在△ ( http: / / www.21cnjy.com )ABC和△DEF中,已知AB=DE,BC=EF,根据(SAS)判定△ABC≌△DEF,还需的条件是( ) ( http: / / www.21cnjy.com )A.∠A=∠D B.∠B=∠E C.∠C=∠F D.以上三个均可以练2.如下图所示,已知∠1=∠2,AO=BO,求证:△AOC≌△BOC. ( http: / / www.21cnjy.com )2.先证明对应边或对应角相等,再证明三角形全等【例2】(2015春 启东市校级月考)如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE. ( http: / / www.21cnjy.com )总结:没有直接给出能证明三角形全等的条件时,(1)先根据已知条件或求证 ( http: / / www.21cnjy.com )的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件;如果已知两边,则要找第三边或夹角;如果已知一角和该角的一边,则需要找夹角的另一条边;(2)在证明三角形全等时,有些题目的条件含而不露,通常要挖掘出隐含条件,比如公共边、对顶角等,从而为解题所用;(3)有些条件需要用到线段与角的和差关系才能得到.练3.(2014 房山区二模)如图,已知AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE. ( http: / / www.21cnjy.com )练4.(2014 永春县质检)已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE.求证:△AEC≌△BDC. ( http: / / www.21cnjy.com )3.先用SAS证明三角形全等,再证对应边、对应角相等【例3】(1)(2014 十堰)如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:∠B=∠C. ( http: / / www.21cnjy.com )(2)(2015春 鼓楼区校级月考)如图,点E,F在AC上,AB∥CD,AB=CD,AE=CF.求证:BF=DE. ( http: / / www.21cnjy.com )总结:综合利用三角形全等的判定与性质解题步骤如下:(1)由问题中的条件,依据三角形全等的判定方法证明两个三角形全等;(2)由三角形全等的性质证得对应角相等、对应边相等.练5.(2013秋 涞水县期末)如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为( ) ( http: / / www.21cnjy.com ) A.50° B.30° C.80° D.100°练6.(2014春 锦州校级期中)如图 ( http: / / www.21cnjy.com ),点B,E,C,F在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,若∠ =∠ ,则△ABC≌△DEF,所以BC= ,因此BE= . ( http: / / www.21cnjy.com )
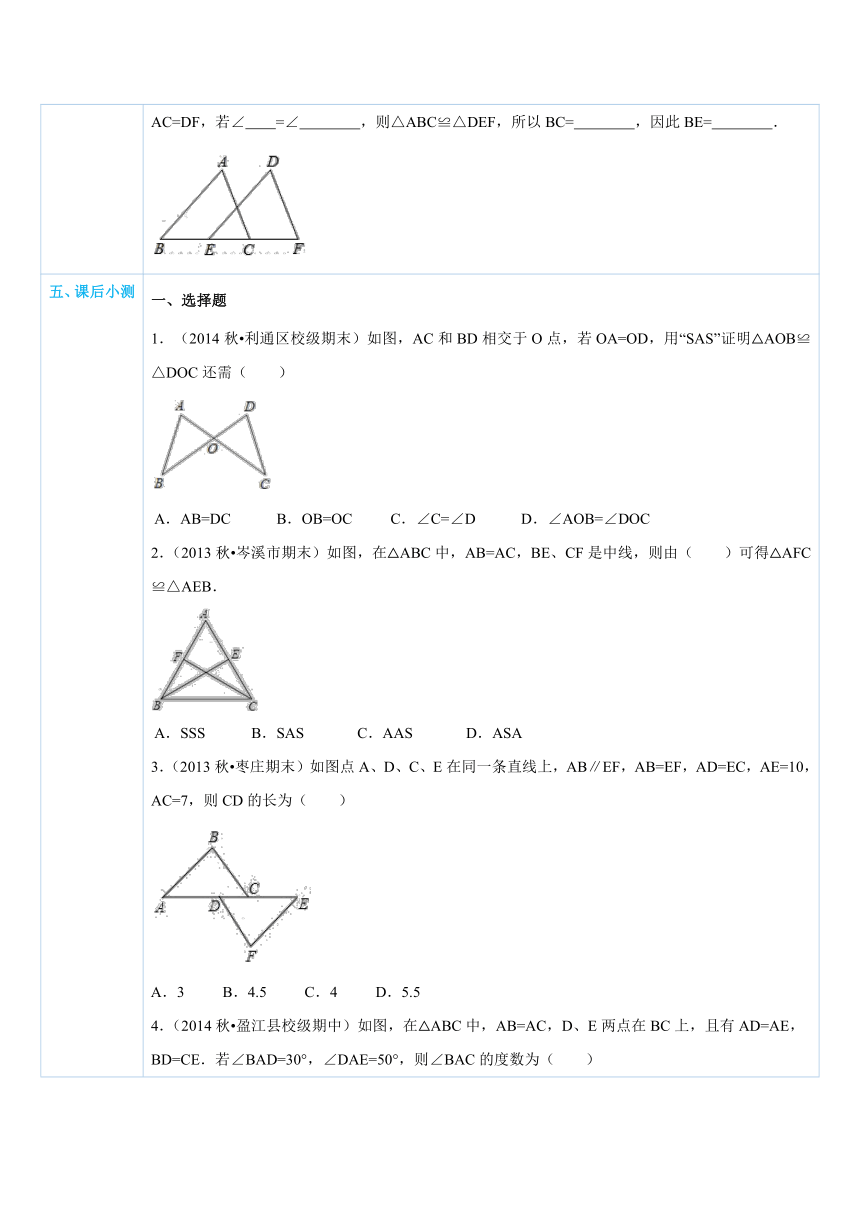
五、课后小测 一、选择题1.(2014秋 利通区校级期末)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( ) ( http: / / www.21cnjy.com )A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC2.(2013秋 岑溪市期末)如图,在△ABC中,AB=AC,BE、CF是中线,则由( )可得△AFC≌△AEB. ( http: / / www.21cnjy.com )A.SSS B.SAS C.AAS D.ASA3.(2013秋 枣庄期末)如图点 ( http: / / www.21cnjy.com )A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=7,则CD的长为( ) ( http: / / www.21cnjy.com )A.3 B.4.5 C.4 D.5.54.(2014秋 盈江县校级期中) ( http: / / www.21cnjy.com )如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC的度数为( ) ( http: / / www.21cnjy.com )A.130° B.120° C.110° D.100°5.(2014秋 湛江校级期中)如图,若AB与CD互相平分于O,则下列结论中错误的是( ) ( http: / / www.21cnjy.com )A.∠C=∠D B.AD=BC C.AD∥BC D.AB=CD二、填空题6.(2013秋 东莞市校级期末)如图,AE=AF,AB=AC,∠A=60°,∠B=26°,则∠BOC= . ( http: / / www.21cnjy.com )7.(2014秋 秀洲区校级期中)如图,AE=BF,AD∥BC,AD=BC,则有△ADF≌ ,且DF= . ( http: / / www.21cnjy.com )三、解答题8.(2014 房县三模)如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.求证:△ACD≌△BCE. ( http: / / www.21cnjy.com )9.(2014 厦门校级一模)如图,A、B、C、D四点在同一条直线上,AB=CD,EC=DF,EC∥DF.求证:△ACE≌BDF. ( http: / / www.21cnjy.com )10.(2014 梧州)如图,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF. ( http: / / www.21cnjy.com )11.(2014 昆明)已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF.求证:∠E=∠F. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】直接根据SAS可证明△ABC≌△DEF.
证明:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
练1.【解析】根据三角形全等的判定中的SAS,即两边夹角.做题时根据已知条件,结合全等的判定方法逐一验证,要由位置选择方法.
解:要使两三角形全等,且SAS已知AB=DE,BC=EF,还差夹角,即∠B=∠E;
A、C都不满足要求,D也就不能选取.
故选B.
练2.【解析】两个三角形包含一个公共边,结合已知条件,根据SAS可证明△AOC≌△BOC.
证明:在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS).
【例2】【解析】根据平行线的性质及全等三角形的判定定理“SAS”证得结论.
证明:∵AE=CF,
∴AE﹣EF=CF﹣EF,即AF=CE.
又∵AD∥BC,
∴∠A=∠C.
∵在△ADF与△CBE中,
,
∴△ADF≌△CBE(SAS).
练3.【解析】已知∠1=∠2,∠BAE是公共 ( http: / / www.21cnjy.com )角,从而可推出∠DAE=∠BAC,已知AB=AD,AC=AE,从而可以利用SAS来判定△ABC≌△ADE.
证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠DAE=∠BAC.
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS).
练4.【解析】根据∠ACD ( http: / / www.21cnjy.com )=∠BCE,可得出∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD.根据边角边公理可得出△AEC≌△BDC.
证明:在△AEC和△BDC中,
∵点C是线段AB的中点,
∴AC=BC,
∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠BCD,
在△AEC和△BDC中,
,
∴△AEC≌△BDC(SAS).
点评:本题考查了全等三角形的判定SAS.
【例3】(1)【解析】首 ( http: / / www.21cnjy.com )先根据条件AB=AC,AD=AE,再加上公共角∠A=∠A可利用“SAS”定理证明△ABE≌△ACD,进而得到∠B=∠C.
证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS).
∴∠B=∠C.
(2)【解析】先由平行线的性质得出内错角相等,再证出AF=CE,根据SAS证明△ABF≌△CDE,由全等三角形的对应边相等即可得出结论.
证明:∵AB∥CD,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS),
∴BF=DE.
练5.【解析】利用SAS可证明△AOD≌△COB,则∠D=∠B=30°.
解:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△AOD≌△COB(SAS),
∴∠D=∠B=30°.
故选B.
练6.【解析】根据三角形全等的判定方法SAS,若∠A=∠D时,两个三角形全等,得出对应边相等,得出结果.
解:若∠A=∠D时,△ABC≌△DEF;
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF,
∴BE=CF;
故答案为:∠A=∠D,EF,CF.
课后小测答案:
一、选择题
1.【解析】A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;
B、∵在△AOB和△DOC中,
∴△AOB≌△DOC(SAS),故本选项正确;
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;
D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;
故选B.
2.【解析】∵BE、CF是中线,
∴AE=AC,AF=AB,
∵AB=AC,
∴AF=AE,
在△AFC和△AEB中,
∴△AFC≌△AEB(SAS),
故选:B.
3.【解析】∵AB∥EF,
∴∠A=∠E,
∵AD=EC,
∴AD+DC=EC+DC,即AC=ED,
在△ABC和△EFD中
,
∴△ABC≌△EFD(SAS),
∴AC=ED=7,
∴CD=AC+ED﹣AE=7+7﹣10=4.
故选C.
4.【解析】∵△ABC中,AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE,
∴∠BAD=∠CAE=30°
∴∠BAC=∠BAD+∠DAE+∠CAE=30°+50°+30°=110°
故选C.
5.【解析】∵AB与CD互相平分,
∴OA=OB,OD=OC
又∵∠AOD=∠COB(对顶角相等),
∴△AOD≌△BOC(SAS),
∴∠C=∠D、AD=BC,
∴AD∥BC(内错角相等,两直线平行),
即A、B、C是正确的,只有D是错误的.
故选D.
二、填空题
6.【解析】在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠B=∠C=26°,
∵∠BFC=∠A+∠B=60°+26°=86°,
∴∠BOC=∠BFC+∠C=86°+26°=112°.
故答案为112°.
7.【解析】∵AE=BF,∴AF=BE,
∵AD∥BC,∴∠A=∠D,
又AD=BC,
∴△ADF≌△BCE,
∴DF=CE.
故答案为:△BCE,CE.
三、解答题
8.【解析】∵C是线段AB的中点,
∴AC=BC,
∵CD平分∠ACE,CE平分∠BCD,
∴∠ACD=∠ECD,∠BCE=∠ECD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
9.【解析】∵AB=CD,
∴AB+BC=CD+BC,即AC=BD.
又∵EC∥DF,
∴∠ACE=∠BDF.
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS).
10.【解析】AB∥CD,
∴∠DCF=∠ABE,
∵BF=CE,
∴BF﹣EF=CE﹣EF,即CF=BE,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
∴AE=DF.
11.【解析】∵AE∥CF,
∴∠A=∠FCD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠E=∠F.
二、知识回顾 1.什么是全等三角形?全等三角形的性质有哪些?能够完全重合的三角形叫做全等三角形.全等三角形的性质:全等三角形的对应边相等 ( http: / / www.21cnjy.com );全等三角形的对应角相等;全等三角形对应边上的中线、高相等,对应角的平分线相等;全等三角形的周长面积也相等.2.上一课学习的三角形全等的判定方法是什么?三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
三、新知讲解 1.边角边定理三角形全等判定方法2:两边和它们的夹角分别相等的两个三角形全等.(简称SAS)符号语言:在△ABC与△DEF中,∴△ABC≌△DEF(SAS).图示: ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )2.探索边边角两边及其一边所对的角分别相等,两个三角形不一定全等.
四、典例探究 扫一扫,有惊喜哦!1.利用SAS直接证明三角形全等【例1】如图所示,△ABC,△DEF均为锐角三角形,AB=DE,AC=DF,∠A=∠D.求证:△ABC≌△DEF. ( http: / / www.21cnjy.com )总结:运用“边角边”判定两个三角形全等时,(1)同一三角形的边、角要放在等号的同一边,按照“边角边”的顺序书写;(2)注意条件里的三个元素必须齐全,且对应相等;(3)条件里的三个元素必须对应,一个三角形 ( http: / / www.21cnjy.com )中的元素依次是“边—角—边”,另一个三角形的元素也必须依次是“边—角—边”,如果是其他“边—边—角”或“角—边—边”,则两个三角形不一定全等;(4)在条件中,相等的角必须是所给两边的夹角,如果把夹角改为其中一条边的对角,则不一定全等.练1.(2013秋 天元区期末)如图,在△ ( http: / / www.21cnjy.com )ABC和△DEF中,已知AB=DE,BC=EF,根据(SAS)判定△ABC≌△DEF,还需的条件是( ) ( http: / / www.21cnjy.com )A.∠A=∠D B.∠B=∠E C.∠C=∠F D.以上三个均可以练2.如下图所示,已知∠1=∠2,AO=BO,求证:△AOC≌△BOC. ( http: / / www.21cnjy.com )2.先证明对应边或对应角相等,再证明三角形全等【例2】(2015春 启东市校级月考)如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE. ( http: / / www.21cnjy.com )总结:没有直接给出能证明三角形全等的条件时,(1)先根据已知条件或求证 ( http: / / www.21cnjy.com )的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件;如果已知两边,则要找第三边或夹角;如果已知一角和该角的一边,则需要找夹角的另一条边;(2)在证明三角形全等时,有些题目的条件含而不露,通常要挖掘出隐含条件,比如公共边、对顶角等,从而为解题所用;(3)有些条件需要用到线段与角的和差关系才能得到.练3.(2014 房山区二模)如图,已知AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE. ( http: / / www.21cnjy.com )练4.(2014 永春县质检)已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE.求证:△AEC≌△BDC. ( http: / / www.21cnjy.com )3.先用SAS证明三角形全等,再证对应边、对应角相等【例3】(1)(2014 十堰)如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:∠B=∠C. ( http: / / www.21cnjy.com )(2)(2015春 鼓楼区校级月考)如图,点E,F在AC上,AB∥CD,AB=CD,AE=CF.求证:BF=DE. ( http: / / www.21cnjy.com )总结:综合利用三角形全等的判定与性质解题步骤如下:(1)由问题中的条件,依据三角形全等的判定方法证明两个三角形全等;(2)由三角形全等的性质证得对应角相等、对应边相等.练5.(2013秋 涞水县期末)如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为( ) ( http: / / www.21cnjy.com ) A.50° B.30° C.80° D.100°练6.(2014春 锦州校级期中)如图 ( http: / / www.21cnjy.com ),点B,E,C,F在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,若∠ =∠ ,则△ABC≌△DEF,所以BC= ,因此BE= . ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014秋 利通区校级期末)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( ) ( http: / / www.21cnjy.com )A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC2.(2013秋 岑溪市期末)如图,在△ABC中,AB=AC,BE、CF是中线,则由( )可得△AFC≌△AEB. ( http: / / www.21cnjy.com )A.SSS B.SAS C.AAS D.ASA3.(2013秋 枣庄期末)如图点 ( http: / / www.21cnjy.com )A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=7,则CD的长为( ) ( http: / / www.21cnjy.com )A.3 B.4.5 C.4 D.5.54.(2014秋 盈江县校级期中) ( http: / / www.21cnjy.com )如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC的度数为( ) ( http: / / www.21cnjy.com )A.130° B.120° C.110° D.100°5.(2014秋 湛江校级期中)如图,若AB与CD互相平分于O,则下列结论中错误的是( ) ( http: / / www.21cnjy.com )A.∠C=∠D B.AD=BC C.AD∥BC D.AB=CD二、填空题6.(2013秋 东莞市校级期末)如图,AE=AF,AB=AC,∠A=60°,∠B=26°,则∠BOC= . ( http: / / www.21cnjy.com )7.(2014秋 秀洲区校级期中)如图,AE=BF,AD∥BC,AD=BC,则有△ADF≌ ,且DF= . ( http: / / www.21cnjy.com )三、解答题8.(2014 房县三模)如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.求证:△ACD≌△BCE. ( http: / / www.21cnjy.com )9.(2014 厦门校级一模)如图,A、B、C、D四点在同一条直线上,AB=CD,EC=DF,EC∥DF.求证:△ACE≌BDF. ( http: / / www.21cnjy.com )10.(2014 梧州)如图,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF. ( http: / / www.21cnjy.com )11.(2014 昆明)已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF.求证:∠E=∠F. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】直接根据SAS可证明△ABC≌△DEF.
证明:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
练1.【解析】根据三角形全等的判定中的SAS,即两边夹角.做题时根据已知条件,结合全等的判定方法逐一验证,要由位置选择方法.
解:要使两三角形全等,且SAS已知AB=DE,BC=EF,还差夹角,即∠B=∠E;
A、C都不满足要求,D也就不能选取.
故选B.
练2.【解析】两个三角形包含一个公共边,结合已知条件,根据SAS可证明△AOC≌△BOC.
证明:在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS).
【例2】【解析】根据平行线的性质及全等三角形的判定定理“SAS”证得结论.
证明:∵AE=CF,
∴AE﹣EF=CF﹣EF,即AF=CE.
又∵AD∥BC,
∴∠A=∠C.
∵在△ADF与△CBE中,
,
∴△ADF≌△CBE(SAS).
练3.【解析】已知∠1=∠2,∠BAE是公共 ( http: / / www.21cnjy.com )角,从而可推出∠DAE=∠BAC,已知AB=AD,AC=AE,从而可以利用SAS来判定△ABC≌△ADE.
证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠DAE=∠BAC.
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS).
练4.【解析】根据∠ACD ( http: / / www.21cnjy.com )=∠BCE,可得出∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD.根据边角边公理可得出△AEC≌△BDC.
证明:在△AEC和△BDC中,
∵点C是线段AB的中点,
∴AC=BC,
∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠BCD,
在△AEC和△BDC中,
,
∴△AEC≌△BDC(SAS).
点评:本题考查了全等三角形的判定SAS.
【例3】(1)【解析】首 ( http: / / www.21cnjy.com )先根据条件AB=AC,AD=AE,再加上公共角∠A=∠A可利用“SAS”定理证明△ABE≌△ACD,进而得到∠B=∠C.
证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS).
∴∠B=∠C.
(2)【解析】先由平行线的性质得出内错角相等,再证出AF=CE,根据SAS证明△ABF≌△CDE,由全等三角形的对应边相等即可得出结论.
证明:∵AB∥CD,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS),
∴BF=DE.
练5.【解析】利用SAS可证明△AOD≌△COB,则∠D=∠B=30°.
解:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△AOD≌△COB(SAS),
∴∠D=∠B=30°.
故选B.
练6.【解析】根据三角形全等的判定方法SAS,若∠A=∠D时,两个三角形全等,得出对应边相等,得出结果.
解:若∠A=∠D时,△ABC≌△DEF;
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF,
∴BE=CF;
故答案为:∠A=∠D,EF,CF.
课后小测答案:
一、选择题
1.【解析】A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;
B、∵在△AOB和△DOC中,
∴△AOB≌△DOC(SAS),故本选项正确;
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;
D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;
故选B.
2.【解析】∵BE、CF是中线,
∴AE=AC,AF=AB,
∵AB=AC,
∴AF=AE,
在△AFC和△AEB中,
∴△AFC≌△AEB(SAS),
故选:B.
3.【解析】∵AB∥EF,
∴∠A=∠E,
∵AD=EC,
∴AD+DC=EC+DC,即AC=ED,
在△ABC和△EFD中
,
∴△ABC≌△EFD(SAS),
∴AC=ED=7,
∴CD=AC+ED﹣AE=7+7﹣10=4.
故选C.
4.【解析】∵△ABC中,AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE,
∴∠BAD=∠CAE=30°
∴∠BAC=∠BAD+∠DAE+∠CAE=30°+50°+30°=110°
故选C.
5.【解析】∵AB与CD互相平分,
∴OA=OB,OD=OC
又∵∠AOD=∠COB(对顶角相等),
∴△AOD≌△BOC(SAS),
∴∠C=∠D、AD=BC,
∴AD∥BC(内错角相等,两直线平行),
即A、B、C是正确的,只有D是错误的.
故选D.
二、填空题
6.【解析】在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠B=∠C=26°,
∵∠BFC=∠A+∠B=60°+26°=86°,
∴∠BOC=∠BFC+∠C=86°+26°=112°.
故答案为112°.
7.【解析】∵AE=BF,∴AF=BE,
∵AD∥BC,∴∠A=∠D,
又AD=BC,
∴△ADF≌△BCE,
∴DF=CE.
故答案为:△BCE,CE.
三、解答题
8.【解析】∵C是线段AB的中点,
∴AC=BC,
∵CD平分∠ACE,CE平分∠BCD,
∴∠ACD=∠ECD,∠BCE=∠ECD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
9.【解析】∵AB=CD,
∴AB+BC=CD+BC,即AC=BD.
又∵EC∥DF,
∴∠ACE=∠BDF.
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS).
10.【解析】AB∥CD,
∴∠DCF=∠ABE,
∵BF=CE,
∴BF﹣EF=CE﹣EF,即CF=BE,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(SAS),
∴AE=DF.
11.【解析】∵AE∥CF,
∴∠A=∠FCD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠E=∠F.
