【多媒体导学案】人教版数学八年级上册第12章第6课时全等三角形的判定(开放型问题)(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学八年级上册第12章第6课时全等三角形的判定(开放型问题)(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览


文档简介
一、学习目标 1.判断能证明三角形全等的条件;2.判断三角形全等能推出的结论;3.探索全等三角形判定的综合问题.
二、知识回顾 1.三角形全等的证明思路:①要证什么?②已知什么?③还缺什么?已知条件证明思路两边一边一角两角2.四种判定方法的图例说明: ( http: / / www.21cnjy.com )
三、新知讲解 1. 什么是开放题所谓开放题,即为答案不 ( http: / / www.21cnjy.com )唯一的问题,其主要 ( http: / / www.21cnjy.com )特征是答案的多样性和多层次性.由于这类题综合性强、解题方法灵活多变,结果往往具有开放性,因而需观察、实验、猜测、分析和推理,同时运用树形结合、分类讨论等数学思想.2. 开放题问题类型及解题策略(1)条件开放与探索型问题.从结论出发,执果索因,逆向推理,逐步探求结论成立的条件或把可能产生结论的条件一一列出,逐个分析.(2)结论开放与探索型问题.从剖析题意入手,充分捕捉题设信息,通过由因导果,顺向推理或联想类比、猜测等,从而获得所求的结论.(3)条件、结论开放与探索型问题.此类问题没有明确的条件和结论,并且符合条件的结论具有多样性,需将已知的信息集中进行分析,探索问题成立所必须具备的条件或特定的条件应该有什么结论,通过这一思维活动得出事物内在联系,从而把握事物的整体性和一般性.
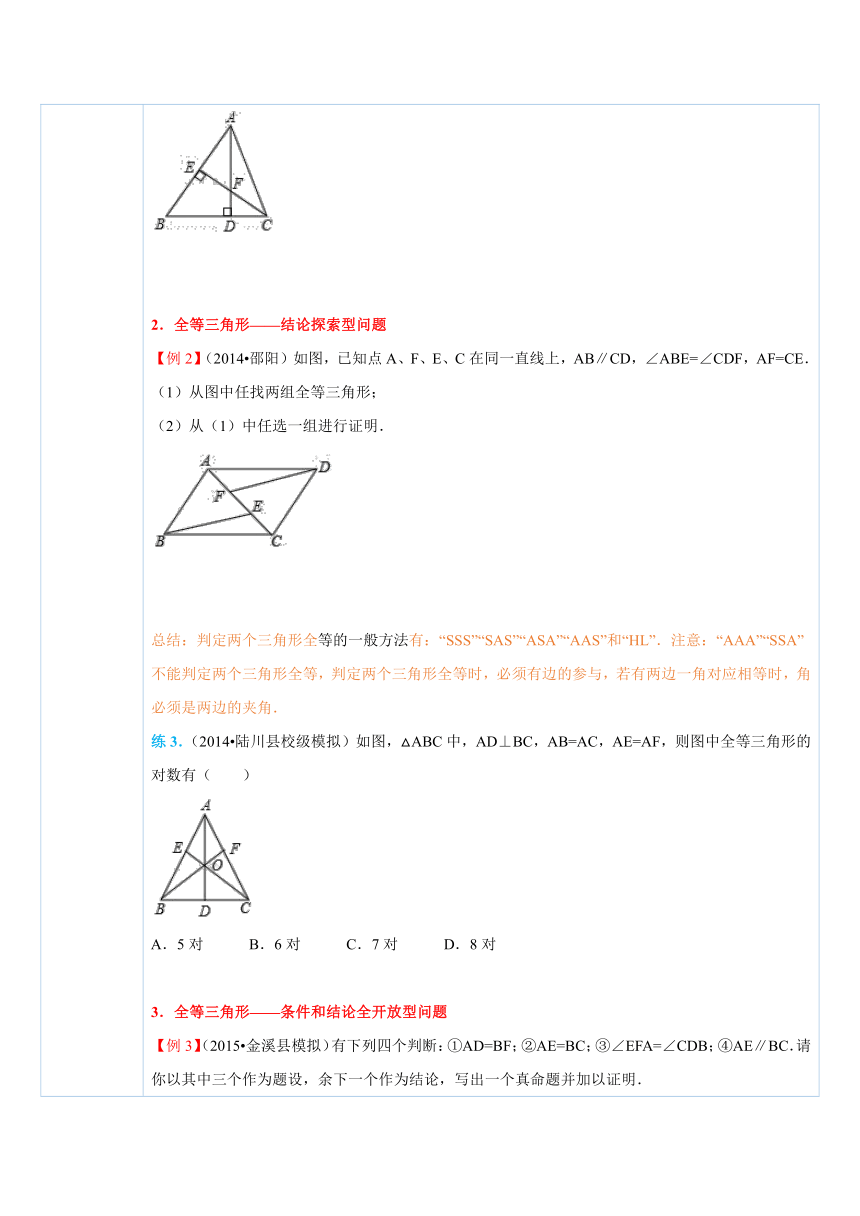
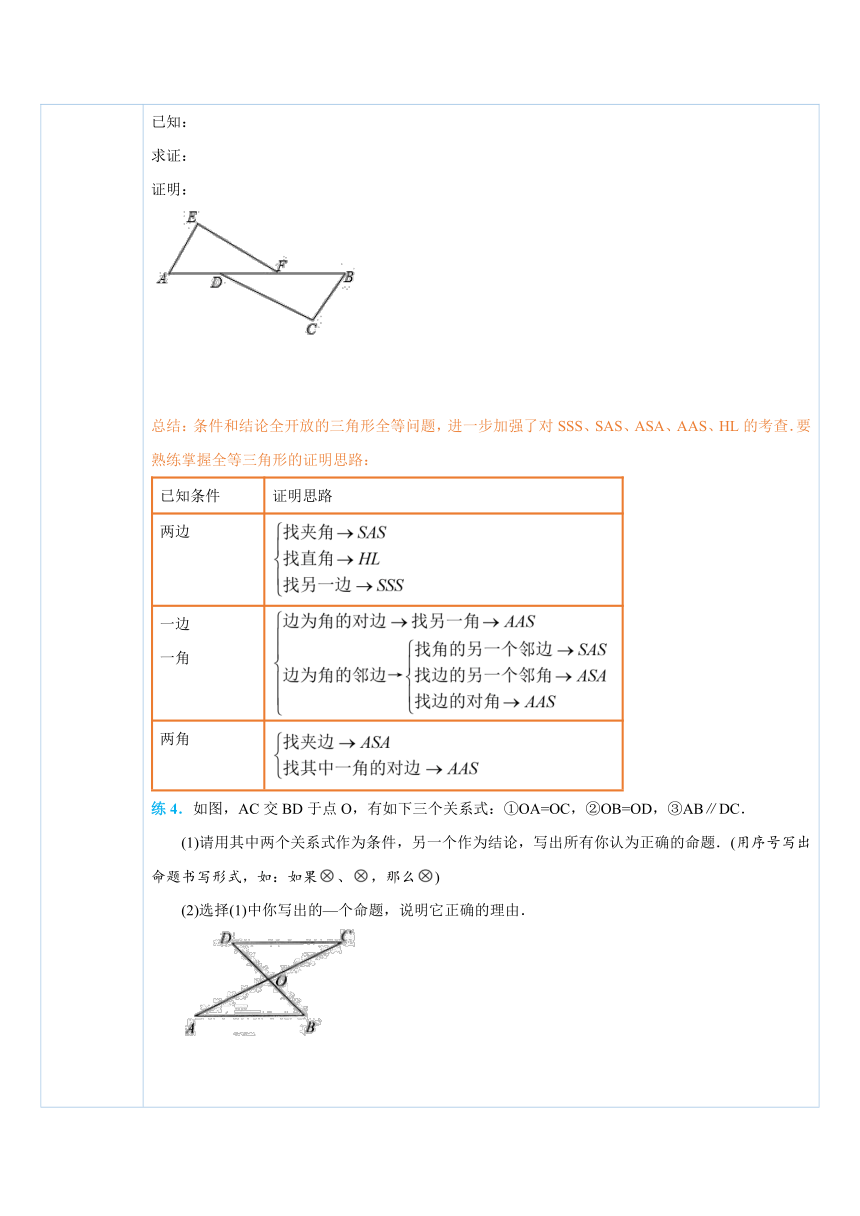
四、典例探究 扫一扫,有惊喜哦!1.全等三角形——补充条件型问题【例1】(2014 漳州)如图,点C,F在 ( http: / / www.21cnjy.com )线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母) ( http: / / www.21cnjy.com )总结:因为全等三角形的判定 ( http: / / www.21cnjy.com )定理有“SAS”“ASA”“AAS”“SSS”,所以此类问题答案是不唯一的. 对于条件添加型的题目,要根据已知条件并结合图形及判定方法来添加一个条件.练1.(2015 滕州市校级模拟)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( ) ( http: / / www.21cnjy.com )A.BD=CD B.AB=AC C.∠B=∠C D.∠BAD=∠CAD练2.(2014秋 宜兴市校级月考)如 ( http: / / www.21cnjy.com )图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加一个适当的条件,使△ADB≌△CEB. ( http: / / www.21cnjy.com )2.全等三角形——结论探索型问题【例2】(2014 邵阳)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明. ( http: / / www.21cnjy.com )总结:判定两个三角形全等的一般方法 ( http: / / www.21cnjy.com )有:“SSS”“SAS”“ASA”“AAS”和“HL”.注意:“AAA”“SSA”不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.练3.(2014 陆川县校级模拟)如图,△ABC中,AD⊥BC,AB=AC,AE=AF,则图中全等三角形的对数有( ) ( http: / / www.21cnjy.com )A.5对 B.6对 C.7对 D.8对3.全等三角形——条件和结论全开放型问题【例3】(2015 金溪县模拟)有 ( http: / / www.21cnjy.com )下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.已知:求证:证明: ( http: / / www.21cnjy.com )总结:条件和结论全开放的三角形全等问题,进一步加强了对SSS、SAS、ASA、AAS、HL的考查.要熟练掌握全等三角形的证明思路:已知条件证明思路两边一边一角两角练4.如图,AC交BD于点O,有如下三个关系式:①OA=OC,②OB=OD,③AB∥DC.(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果、,那么)(2)选择(1)中你写出的—个命题,说明它正确的理由. ( http: / / www.21cnjy.com )
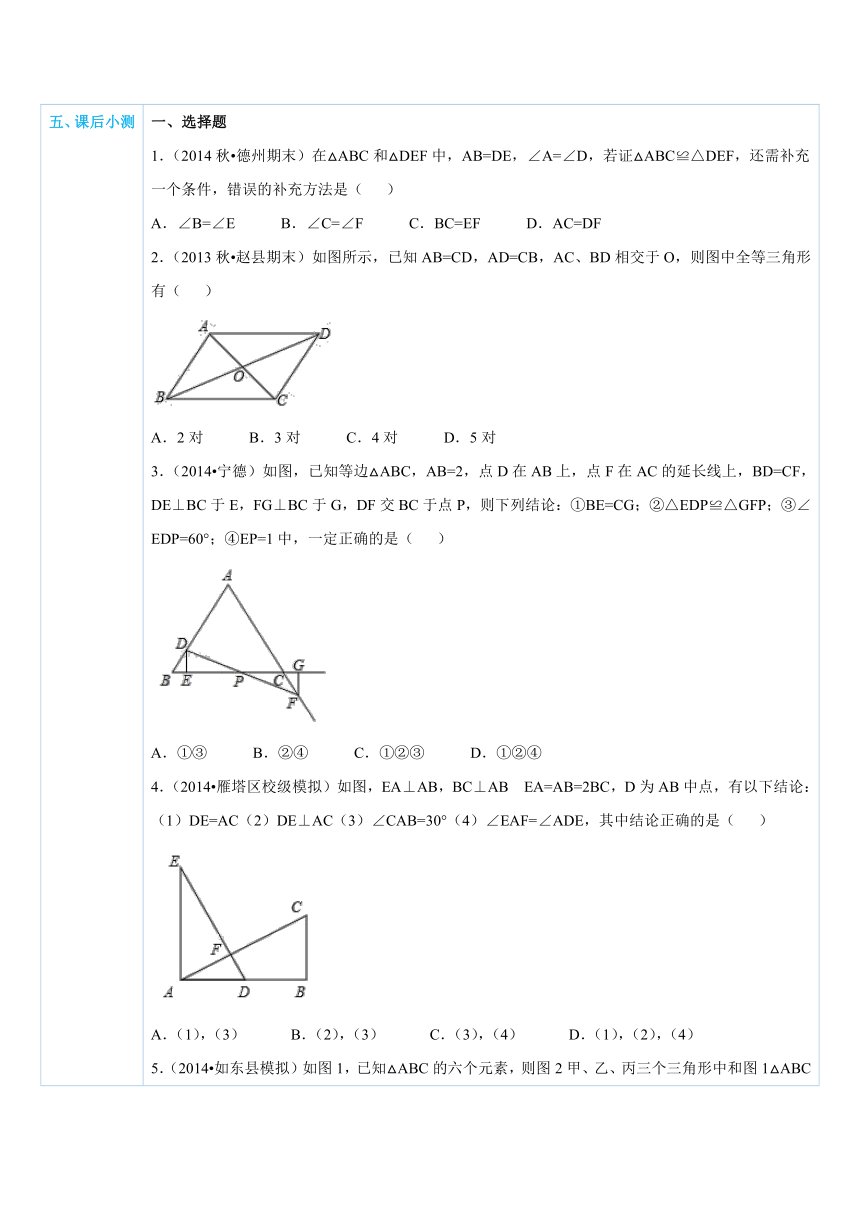
五、课后小测 一、选择题1.(2014秋 德州期末)在△ABC和△D ( http: / / www.21cnjy.com )EF中,AB=DE,∠A=∠D,若证△ABC≌△DEF,还需补充一个条件,错误的补充方法是( )A.∠B=∠E B.∠C=∠F C.BC=EF D.AC=DF2.(2013秋 赵县期末)如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( ) ( http: / / www.21cnjy.com )A.2对 B.3对 C.4对 D.5对3.(2014 宁德)如图 ( http: / / www.21cnjy.com ),已知等边△ABC,AB=2,点D在AB上,点F在AC的延长线上,BD=CF,DE⊥BC于E,FG⊥BC于G,DF交BC于点P,则下列结论:①BE=CG;②△EDP≌△GFP;③∠EDP=60°;④EP=1中,一定正确的是( ) ( http: / / www.21cnjy.com )A.①③ B.②④ C.①②③ D.①②④4.(2014 雁塔区校 ( http: / / www.21cnjy.com )级模拟)如图,EA⊥AB,BC⊥AB EA=AB=2BC,D为AB中点,有以下结论:(1)DE=AC(2)DE⊥AC(3)∠CAB=30°(4)∠EAF=∠ADE,其中结论正确的是( ) ( http: / / www.21cnjy.com )A.(1),(3) B.(2),(3) C.(3),(4) D.(1),(2),(4)5.(2014 如东县模拟)如图1,已知△ABC的六个元素,则图2甲、乙、丙三个三角形中和图1△ABC全等的图形是( ) ( http: / / www.21cnjy.com )A.甲乙 B.丙 C.乙丙 D.乙6.(2014秋 嘉荫县期末)如图,在 ( http: / / www.21cnjy.com )△ABC中,AB=AC,AE=AF,AD⊥BC于点D,且点E、F在BC上,则图中全等的直角三角形共有( ) ( http: / / www.21cnjy.com )A.1对 B.2对 C.3对 D.4对二、填空题7.(2014秋 肥东县期末)在△AB ( http: / / www.21cnjy.com )C中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是______. ( http: / / www.21cnjy.com )8.(2013春 沧浪区校级期末) ( http: / / www.21cnjy.com )如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=____时,△ABC和△PQA全等. ( http: / / www.21cnjy.com )9.(2014秋 岑溪市期中)如图所示, ( http: / / www.21cnjy.com )∠B=∠D=90°,要使△ABC≌△ADC,还需添加一个条件,这个条件可以是_________(只需填一个即可). ( http: / / www.21cnjy.com )三、解答题10.(2012秋 广州校级期中)如 ( http: / / www.21cnjy.com )图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论. ( http: / / www.21cnjy.com )11.(2015 金溪县模拟)请从以下三个等式中,选出一个等式天在横线上,并加以证明.等式:AB=CD,∠A=∠C,∠AEB=∠CFD,已知:AB∥CD,BE=DF,_______求证:△ABE≌△CDF.证明: ( http: / / www.21cnjy.com )12.(2014 徐州模拟)已知:如图,△ABC中,AB=AC,点D为BC的中点,连接AD.(1)请你写出两个正确结论:①__________;②__________;(2)当∠B=60°时,还可以得出哪些正确结论?(只需写出一个)(3)请在图中过点D作于DM⊥AB于M,DN⊥AC于N.求证:△DBM≌△DCN. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】由已知先推出BC=EF,添加条件AC=DF,根据“SAS”可推出两三角形全等.
解:AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,
即BC=EF.
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
练1.【解析】利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.
解:A、∵∠1=∠2,AD为公共边,若BD=CD,则△ABD≌△ACD(SAS);
B、∵∠1=∠2,AD为公共边,若AB=AC,不符合全等三角形判定定理,不能判定△ABD≌△ACD;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);
D、∵∠1=∠2,AD为公共边,若∠BAD=∠CAD,则△ABD≌△ACD(ASA);
故选:B.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
练2.【解析】要使△ADB≌△CEB, ( http: / / www.21cnjy.com )已知∠B为公共角,∠BEC=∠BDA,具备了两组角对应相等,故添加AB=BC或BE=BD或EC=AD后可分别根据AAS、ASA、AAS能判定△ADB≌△CEB.
解:AB=BC,AD⊥BC,CE⊥AB,B=∠B
∴△ADB≌△CEB(AAS).
答案:AB=BC.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
点评:AAA、SSA不能判定两 ( http: / / www.21cnjy.com )个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.添加条件时,要首选明显的、简单的,由易到难.
【例2】【解析】(1)根据题目所给条件可分析出△ABE≌△CDF,△AFD≌△CEB;
(2)根据AB∥CD可得∠1=∠2,根据AF=CE可得AE=FC,然后再证明△ABE≌△CDF即可.
解:(1)△ABE≌△CDF,△AFD≌△CEB;
(2)∵AB∥CD,
( http: / / www.21cnjy.com )
∴∠1=∠2,
∵AF=CE,
∴AF+EF=CE+EF,
即AE=FC.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
练3.【解析】三角形全等条件中必须是三个元素,并且一定有一组对应边相等.做题时要从已知条件开始,结合判定方法对选项逐一验证.
解:∵△ABC中,AD⊥BC,AB=AC,
∴BD=CD,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,
又AE=AF,AO=AO,
∴△AOE≌△AOF,
EO=FO,
进一步证明可得△BOD≌△COD,△BOE≌△COF,△AOB≌△AOC,△ABF≌△ACE,△BCE≌△CBF,共7对.
故选:C.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理.
【例3】【解析】由已知AD=BF,证出AF=BD,再由平行线AE∥BC得出∠A=∠B,证明△AEF≌△BCD,即可得出∠EFA=∠CDB.
解:已知:AD=BF,AE=BC,AE∥BC;
求证:∠EFA=∠CDB;
证明:∵AD=BF,
∴AD+DF=BF+DF,
即AF=BD.
∵AE∥BC,
∴∠A=∠B,
在△AEF和△BCD中,
∴△AEF≌△BCD(SAS),
∴∠EFA=∠CDB.
点评:本题考查了全等三角形的判定与性质以及命题与定理;熟练掌握全等三角形的判定方法是解题的关键.
练4.【解析】(1)如果①、②,那么③,或如果①、③,那么②,如果②、③,那么①;
(2)下面选择“如果①、②,那么③”加以证明.
证明:在△AOB和△COD中,
∴△AOB≌△COD,
∴∠A=∠C,
∴AB∥DC.
课后小测答案:
一、选择题
1.【解析】根据已知及全等三角形的判定方法对各个选项进行分析,从而得到答案.
解:A、正确,符合判定ASA;
B、正确,符合判定AAS;
C、不正确,满足SSA没有与之对应的判定方法,不能判定全等;
D、正确,符合判定SAS.
故选:C.
点评:此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有AAS,SAS,SSS,HL等.
2.【解析】先证明四边形ABCD是平行四边形,再根据平行四边形的对角线互相平分解答.
解:∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∴△ABO≌△CDO,△ADO≌△CBO,
又△ABC≌△CDA,△ABD≌△CDB,
∴图中全等三角形有四对.
故选:C.
点评:本题主要考查全等三角形的判定,先证明四边形ABCD是平行四边形是解题的关键.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
3.【解析】由等边三角形的性质可以得出 ( http: / / www.21cnjy.com )△DEB≌△FGC,就可以得出BE=CG,DE=FG,就可以得出△DEP≌△FGP,得出∠EDP=∠GFP,EP=PG,得出PC+BE=PE,就可以得出PE=1,从而得出结论.
解:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠ACB=60°.
∵∠ACB=∠GCF,
∵DE⊥BC,FG⊥BC,
∴∠DEB=∠FGC=∠DEP=90°.
在△DEB和△FGC中,
,
∴△DEB≌△FGC(AAS),
∴BE=CG,DE=FG,故①正确;
在△DEP和△FGP中,
,
∴△DEP≌△FGP(AAS),故②正确;
∴PE=PG∠EDP=∠GFP≠60°,故③错误;
∵PG=PC+CG,
∴PE=PC+BE.
∵PE+PC+BE=2,
∴PE=1.故④正确.
正确的有①②④,
故选:D.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.
4.【解析】本题条件较为充分,EA⊥AB, ( http: / / www.21cnjy.com )BC⊥AB,EA=AB=2BC,D为AB中点可得两直角三角形全等,然后利用三角形的性质问题可解决.做题时,要结合已知条件与全等的判定方法对选项逐一验证.
解:∵EA⊥AB,BC⊥AB,∴∠EAB=∠ABC=90°
Rt△EAD与Rt△ABC
∵D为AB中点,∴AB=2AD
又EA=AB=2BC
∴AD=BC
∴Rt△EAD≌Rt△ABC
∴DE=AC,∠C=∠ADE,∠E=∠FAD
又∠EAF+∠DAF=90°∴∠EAF+∠E=90°
∴∠EFA=180°﹣90°=90°,即DE⊥AC,
∠EAF+∠DAF=90°,∠C+∠DAF=90°
∴∠C=∠EAF,∠C=∠ADE
∴∠EAF=∠ADE
故选:D.
点评:本题考查了全等三角形的判定与性质;全等三角形问题要认真观察已知与图形,仔细寻找全等条件证出全等,再利用全等的性质解决问题.
5.【解析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
解:已知图1的△ABC中,∠B=50°,BC=a,AB=c,AC=b,∠C=58°,∠A=72°,
图2中,甲:只有一个角和∠B相等,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;
乙:符合SAS定理,能推出两三角形全等;
丙:符合AAS定理,能推出两三角形全等;
故选:C.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
6.【解析】如图,运用等腰三角形的性质证明BD=CD,DE=DF;证明△ABD≌△ACD,△AED≌△AFD,即可解决问题.
解:如图,∵AB=AC,AE=AF,AD⊥BC,
( http: / / www.21cnjy.com )
∴BD=CD,DE=DF;
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SAS),
同理可证△AED≌△AFD;
故选:B.
点评:该题主要考查了全等三角形的判定问题、等腰三角形的性质及其应用问题;灵活运用全等三角形的判定问题、等腰三角形的性质是解题的关键.
二、填空题、
7.【解析】根据角平分线的性质,和全等三角形的判定,可证Rt△ASP≌Rt△ARP,得AS=AR;∠PAR=∠PAQ,可证PQ∥AR.
解:连接AP,
( http: / / www.21cnjy.com )
在Rt△ASP和Rt△ARP中
PR=PS,PA=PA
所以Rt△ASP≌Rt△ARP
所以①AS=AR正确
因为AQ=PQ
所以∠QAP=∠QPA
又因为Rt△ASP≌Rt△ARP
所以∠PAR=∠PAQ
于是∠RAP=∠QPA
所以②PQ∥AR正确
③△BRP≌△CSP,根据现有条件无法确定其全等.
故填①②.
点评:此题考查了到角平分线的性质及全等三角形的判定和平行线的判定定理;正确作出辅助线是解答本题的关键.
8.【解析】当AP=5或10时,△ABC和△PQA全等,根据HL定理推出即可.
解:当AP=5或10时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=5=BC时,
在Rt△ACB和Rt△QAP中
∴Rt△ACB≌Rt△QAP(HL),
②当AP=10=AC时,
在Rt△ACB和Rt△PAQ中
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:5或10.
点评:本题考查了全等三角形的判定定理的应用,注意:判定两直角三角形全等的方法有ASA,AAS,SAS,SSS,HL.
9.【解析】全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,根据判定定理写出一个即可.
解:AB=AD,
理由是:∵∠B=∠D=90°,
∴在Rt△ABC和Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL),
故答案为:AB=AD.
点评:本题考查了全等三角形的 ( http: / / www.21cnjy.com )判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,此题是一道开放型的题目,答案不唯一.
三、解答题
10.【解析】先利用HL判定△CAE≌ ( http: / / www.21cnjy.com )△EBD,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:CE=DE,CE⊥DE,理由如下:
∵AC⊥AB,DB⊥AB,
AC=BE,AE=BD,
∴△CAE≌△EBD.
∴∠CEA=∠D.
∵∠D+∠DEB=90°,
∴∠CEA+∠DEB=90°.
即线段CE与DE的大小与位置关系为相等且垂直.
点评:此题主要考查学生对全等三角形的性 ( http: / / www.21cnjy.com )质及全等三角形的判定方法的掌握情况.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意做题格式.
11.【解析】先加上条件,再证明,根据所加的条件,利用
证明:∵AB∥CD,
∴∠B=∠D,
在△ABE和△CDF中,
,
∴△ABE≌△CDF.
点评:本题是一道开放性的题目,考查了全等三角形的判定,是基础知识比较简单.
12.【解析】(1)根据中点的性质及全等三角形的判定,写出两个结论即可;
(2)根据等边三角形的判定定理可得△ABC是等边三角形;
(3)先证明△ABD≌△ACD,再证明△DBM≌△DCN.
解:(1)①BD=CD;②△ABD≌△ACD;
(2)∵AB=AC,∠B=60°,
∴△ABC是等边三角形.
(3)在Rt△ABD和Rt△ACD中,
( http: / / www.21cnjy.com )
,
∴△ABD≌△ACD,
∴∠ABD=∠ACD,
在Rt△DBM和Rt△DCN中,
,
∴△DBM≌△DCN.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
二、知识回顾 1.三角形全等的证明思路:①要证什么?②已知什么?③还缺什么?已知条件证明思路两边一边一角两角2.四种判定方法的图例说明: ( http: / / www.21cnjy.com )
三、新知讲解 1. 什么是开放题所谓开放题,即为答案不 ( http: / / www.21cnjy.com )唯一的问题,其主要 ( http: / / www.21cnjy.com )特征是答案的多样性和多层次性.由于这类题综合性强、解题方法灵活多变,结果往往具有开放性,因而需观察、实验、猜测、分析和推理,同时运用树形结合、分类讨论等数学思想.2. 开放题问题类型及解题策略(1)条件开放与探索型问题.从结论出发,执果索因,逆向推理,逐步探求结论成立的条件或把可能产生结论的条件一一列出,逐个分析.(2)结论开放与探索型问题.从剖析题意入手,充分捕捉题设信息,通过由因导果,顺向推理或联想类比、猜测等,从而获得所求的结论.(3)条件、结论开放与探索型问题.此类问题没有明确的条件和结论,并且符合条件的结论具有多样性,需将已知的信息集中进行分析,探索问题成立所必须具备的条件或特定的条件应该有什么结论,通过这一思维活动得出事物内在联系,从而把握事物的整体性和一般性.
四、典例探究 扫一扫,有惊喜哦!1.全等三角形——补充条件型问题【例1】(2014 漳州)如图,点C,F在 ( http: / / www.21cnjy.com )线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母) ( http: / / www.21cnjy.com )总结:因为全等三角形的判定 ( http: / / www.21cnjy.com )定理有“SAS”“ASA”“AAS”“SSS”,所以此类问题答案是不唯一的. 对于条件添加型的题目,要根据已知条件并结合图形及判定方法来添加一个条件.练1.(2015 滕州市校级模拟)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( ) ( http: / / www.21cnjy.com )A.BD=CD B.AB=AC C.∠B=∠C D.∠BAD=∠CAD练2.(2014秋 宜兴市校级月考)如 ( http: / / www.21cnjy.com )图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加一个适当的条件,使△ADB≌△CEB. ( http: / / www.21cnjy.com )2.全等三角形——结论探索型问题【例2】(2014 邵阳)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明. ( http: / / www.21cnjy.com )总结:判定两个三角形全等的一般方法 ( http: / / www.21cnjy.com )有:“SSS”“SAS”“ASA”“AAS”和“HL”.注意:“AAA”“SSA”不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.练3.(2014 陆川县校级模拟)如图,△ABC中,AD⊥BC,AB=AC,AE=AF,则图中全等三角形的对数有( ) ( http: / / www.21cnjy.com )A.5对 B.6对 C.7对 D.8对3.全等三角形——条件和结论全开放型问题【例3】(2015 金溪县模拟)有 ( http: / / www.21cnjy.com )下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.已知:求证:证明: ( http: / / www.21cnjy.com )总结:条件和结论全开放的三角形全等问题,进一步加强了对SSS、SAS、ASA、AAS、HL的考查.要熟练掌握全等三角形的证明思路:已知条件证明思路两边一边一角两角练4.如图,AC交BD于点O,有如下三个关系式:①OA=OC,②OB=OD,③AB∥DC.(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果、,那么)(2)选择(1)中你写出的—个命题,说明它正确的理由. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014秋 德州期末)在△ABC和△D ( http: / / www.21cnjy.com )EF中,AB=DE,∠A=∠D,若证△ABC≌△DEF,还需补充一个条件,错误的补充方法是( )A.∠B=∠E B.∠C=∠F C.BC=EF D.AC=DF2.(2013秋 赵县期末)如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( ) ( http: / / www.21cnjy.com )A.2对 B.3对 C.4对 D.5对3.(2014 宁德)如图 ( http: / / www.21cnjy.com ),已知等边△ABC,AB=2,点D在AB上,点F在AC的延长线上,BD=CF,DE⊥BC于E,FG⊥BC于G,DF交BC于点P,则下列结论:①BE=CG;②△EDP≌△GFP;③∠EDP=60°;④EP=1中,一定正确的是( ) ( http: / / www.21cnjy.com )A.①③ B.②④ C.①②③ D.①②④4.(2014 雁塔区校 ( http: / / www.21cnjy.com )级模拟)如图,EA⊥AB,BC⊥AB EA=AB=2BC,D为AB中点,有以下结论:(1)DE=AC(2)DE⊥AC(3)∠CAB=30°(4)∠EAF=∠ADE,其中结论正确的是( ) ( http: / / www.21cnjy.com )A.(1),(3) B.(2),(3) C.(3),(4) D.(1),(2),(4)5.(2014 如东县模拟)如图1,已知△ABC的六个元素,则图2甲、乙、丙三个三角形中和图1△ABC全等的图形是( ) ( http: / / www.21cnjy.com )A.甲乙 B.丙 C.乙丙 D.乙6.(2014秋 嘉荫县期末)如图,在 ( http: / / www.21cnjy.com )△ABC中,AB=AC,AE=AF,AD⊥BC于点D,且点E、F在BC上,则图中全等的直角三角形共有( ) ( http: / / www.21cnjy.com )A.1对 B.2对 C.3对 D.4对二、填空题7.(2014秋 肥东县期末)在△AB ( http: / / www.21cnjy.com )C中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是______. ( http: / / www.21cnjy.com )8.(2013春 沧浪区校级期末) ( http: / / www.21cnjy.com )如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=____时,△ABC和△PQA全等. ( http: / / www.21cnjy.com )9.(2014秋 岑溪市期中)如图所示, ( http: / / www.21cnjy.com )∠B=∠D=90°,要使△ABC≌△ADC,还需添加一个条件,这个条件可以是_________(只需填一个即可). ( http: / / www.21cnjy.com )三、解答题10.(2012秋 广州校级期中)如 ( http: / / www.21cnjy.com )图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论. ( http: / / www.21cnjy.com )11.(2015 金溪县模拟)请从以下三个等式中,选出一个等式天在横线上,并加以证明.等式:AB=CD,∠A=∠C,∠AEB=∠CFD,已知:AB∥CD,BE=DF,_______求证:△ABE≌△CDF.证明: ( http: / / www.21cnjy.com )12.(2014 徐州模拟)已知:如图,△ABC中,AB=AC,点D为BC的中点,连接AD.(1)请你写出两个正确结论:①__________;②__________;(2)当∠B=60°时,还可以得出哪些正确结论?(只需写出一个)(3)请在图中过点D作于DM⊥AB于M,DN⊥AC于N.求证:△DBM≌△DCN. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】由已知先推出BC=EF,添加条件AC=DF,根据“SAS”可推出两三角形全等.
解:AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,
即BC=EF.
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
练1.【解析】利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.
解:A、∵∠1=∠2,AD为公共边,若BD=CD,则△ABD≌△ACD(SAS);
B、∵∠1=∠2,AD为公共边,若AB=AC,不符合全等三角形判定定理,不能判定△ABD≌△ACD;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);
D、∵∠1=∠2,AD为公共边,若∠BAD=∠CAD,则△ABD≌△ACD(ASA);
故选:B.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
练2.【解析】要使△ADB≌△CEB, ( http: / / www.21cnjy.com )已知∠B为公共角,∠BEC=∠BDA,具备了两组角对应相等,故添加AB=BC或BE=BD或EC=AD后可分别根据AAS、ASA、AAS能判定△ADB≌△CEB.
解:AB=BC,AD⊥BC,CE⊥AB,B=∠B
∴△ADB≌△CEB(AAS).
答案:AB=BC.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
点评:AAA、SSA不能判定两 ( http: / / www.21cnjy.com )个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.添加条件时,要首选明显的、简单的,由易到难.
【例2】【解析】(1)根据题目所给条件可分析出△ABE≌△CDF,△AFD≌△CEB;
(2)根据AB∥CD可得∠1=∠2,根据AF=CE可得AE=FC,然后再证明△ABE≌△CDF即可.
解:(1)△ABE≌△CDF,△AFD≌△CEB;
(2)∵AB∥CD,
( http: / / www.21cnjy.com )
∴∠1=∠2,
∵AF=CE,
∴AF+EF=CE+EF,
即AE=FC.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
练3.【解析】三角形全等条件中必须是三个元素,并且一定有一组对应边相等.做题时要从已知条件开始,结合判定方法对选项逐一验证.
解:∵△ABC中,AD⊥BC,AB=AC,
∴BD=CD,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,
又AE=AF,AO=AO,
∴△AOE≌△AOF,
EO=FO,
进一步证明可得△BOD≌△COD,△BOE≌△COF,△AOB≌△AOC,△ABF≌△ACE,△BCE≌△CBF,共7对.
故选:C.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理.
【例3】【解析】由已知AD=BF,证出AF=BD,再由平行线AE∥BC得出∠A=∠B,证明△AEF≌△BCD,即可得出∠EFA=∠CDB.
解:已知:AD=BF,AE=BC,AE∥BC;
求证:∠EFA=∠CDB;
证明:∵AD=BF,
∴AD+DF=BF+DF,
即AF=BD.
∵AE∥BC,
∴∠A=∠B,
在△AEF和△BCD中,
∴△AEF≌△BCD(SAS),
∴∠EFA=∠CDB.
点评:本题考查了全等三角形的判定与性质以及命题与定理;熟练掌握全等三角形的判定方法是解题的关键.
练4.【解析】(1)如果①、②,那么③,或如果①、③,那么②,如果②、③,那么①;
(2)下面选择“如果①、②,那么③”加以证明.
证明:在△AOB和△COD中,
∴△AOB≌△COD,
∴∠A=∠C,
∴AB∥DC.
课后小测答案:
一、选择题
1.【解析】根据已知及全等三角形的判定方法对各个选项进行分析,从而得到答案.
解:A、正确,符合判定ASA;
B、正确,符合判定AAS;
C、不正确,满足SSA没有与之对应的判定方法,不能判定全等;
D、正确,符合判定SAS.
故选:C.
点评:此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有AAS,SAS,SSS,HL等.
2.【解析】先证明四边形ABCD是平行四边形,再根据平行四边形的对角线互相平分解答.
解:∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∴△ABO≌△CDO,△ADO≌△CBO,
又△ABC≌△CDA,△ABD≌△CDB,
∴图中全等三角形有四对.
故选:C.
点评:本题主要考查全等三角形的判定,先证明四边形ABCD是平行四边形是解题的关键.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
3.【解析】由等边三角形的性质可以得出 ( http: / / www.21cnjy.com )△DEB≌△FGC,就可以得出BE=CG,DE=FG,就可以得出△DEP≌△FGP,得出∠EDP=∠GFP,EP=PG,得出PC+BE=PE,就可以得出PE=1,从而得出结论.
解:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠ACB=60°.
∵∠ACB=∠GCF,
∵DE⊥BC,FG⊥BC,
∴∠DEB=∠FGC=∠DEP=90°.
在△DEB和△FGC中,
,
∴△DEB≌△FGC(AAS),
∴BE=CG,DE=FG,故①正确;
在△DEP和△FGP中,
,
∴△DEP≌△FGP(AAS),故②正确;
∴PE=PG∠EDP=∠GFP≠60°,故③错误;
∵PG=PC+CG,
∴PE=PC+BE.
∵PE+PC+BE=2,
∴PE=1.故④正确.
正确的有①②④,
故选:D.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.
4.【解析】本题条件较为充分,EA⊥AB, ( http: / / www.21cnjy.com )BC⊥AB,EA=AB=2BC,D为AB中点可得两直角三角形全等,然后利用三角形的性质问题可解决.做题时,要结合已知条件与全等的判定方法对选项逐一验证.
解:∵EA⊥AB,BC⊥AB,∴∠EAB=∠ABC=90°
Rt△EAD与Rt△ABC
∵D为AB中点,∴AB=2AD
又EA=AB=2BC
∴AD=BC
∴Rt△EAD≌Rt△ABC
∴DE=AC,∠C=∠ADE,∠E=∠FAD
又∠EAF+∠DAF=90°∴∠EAF+∠E=90°
∴∠EFA=180°﹣90°=90°,即DE⊥AC,
∠EAF+∠DAF=90°,∠C+∠DAF=90°
∴∠C=∠EAF,∠C=∠ADE
∴∠EAF=∠ADE
故选:D.
点评:本题考查了全等三角形的判定与性质;全等三角形问题要认真观察已知与图形,仔细寻找全等条件证出全等,再利用全等的性质解决问题.
5.【解析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
解:已知图1的△ABC中,∠B=50°,BC=a,AB=c,AC=b,∠C=58°,∠A=72°,
图2中,甲:只有一个角和∠B相等,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;
乙:符合SAS定理,能推出两三角形全等;
丙:符合AAS定理,能推出两三角形全等;
故选:C.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
6.【解析】如图,运用等腰三角形的性质证明BD=CD,DE=DF;证明△ABD≌△ACD,△AED≌△AFD,即可解决问题.
解:如图,∵AB=AC,AE=AF,AD⊥BC,
( http: / / www.21cnjy.com )
∴BD=CD,DE=DF;
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SAS),
同理可证△AED≌△AFD;
故选:B.
点评:该题主要考查了全等三角形的判定问题、等腰三角形的性质及其应用问题;灵活运用全等三角形的判定问题、等腰三角形的性质是解题的关键.
二、填空题、
7.【解析】根据角平分线的性质,和全等三角形的判定,可证Rt△ASP≌Rt△ARP,得AS=AR;∠PAR=∠PAQ,可证PQ∥AR.
解:连接AP,
( http: / / www.21cnjy.com )
在Rt△ASP和Rt△ARP中
PR=PS,PA=PA
所以Rt△ASP≌Rt△ARP
所以①AS=AR正确
因为AQ=PQ
所以∠QAP=∠QPA
又因为Rt△ASP≌Rt△ARP
所以∠PAR=∠PAQ
于是∠RAP=∠QPA
所以②PQ∥AR正确
③△BRP≌△CSP,根据现有条件无法确定其全等.
故填①②.
点评:此题考查了到角平分线的性质及全等三角形的判定和平行线的判定定理;正确作出辅助线是解答本题的关键.
8.【解析】当AP=5或10时,△ABC和△PQA全等,根据HL定理推出即可.
解:当AP=5或10时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=5=BC时,
在Rt△ACB和Rt△QAP中
∴Rt△ACB≌Rt△QAP(HL),
②当AP=10=AC时,
在Rt△ACB和Rt△PAQ中
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:5或10.
点评:本题考查了全等三角形的判定定理的应用,注意:判定两直角三角形全等的方法有ASA,AAS,SAS,SSS,HL.
9.【解析】全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,根据判定定理写出一个即可.
解:AB=AD,
理由是:∵∠B=∠D=90°,
∴在Rt△ABC和Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL),
故答案为:AB=AD.
点评:本题考查了全等三角形的 ( http: / / www.21cnjy.com )判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,此题是一道开放型的题目,答案不唯一.
三、解答题
10.【解析】先利用HL判定△CAE≌ ( http: / / www.21cnjy.com )△EBD,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:CE=DE,CE⊥DE,理由如下:
∵AC⊥AB,DB⊥AB,
AC=BE,AE=BD,
∴△CAE≌△EBD.
∴∠CEA=∠D.
∵∠D+∠DEB=90°,
∴∠CEA+∠DEB=90°.
即线段CE与DE的大小与位置关系为相等且垂直.
点评:此题主要考查学生对全等三角形的性 ( http: / / www.21cnjy.com )质及全等三角形的判定方法的掌握情况.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意做题格式.
11.【解析】先加上条件,再证明,根据所加的条件,利用
证明:∵AB∥CD,
∴∠B=∠D,
在△ABE和△CDF中,
,
∴△ABE≌△CDF.
点评:本题是一道开放性的题目,考查了全等三角形的判定,是基础知识比较简单.
12.【解析】(1)根据中点的性质及全等三角形的判定,写出两个结论即可;
(2)根据等边三角形的判定定理可得△ABC是等边三角形;
(3)先证明△ABD≌△ACD,再证明△DBM≌△DCN.
解:(1)①BD=CD;②△ABD≌△ACD;
(2)∵AB=AC,∠B=60°,
∴△ABC是等边三角形.
(3)在Rt△ABD和Rt△ACD中,
( http: / / www.21cnjy.com )
,
∴△ABD≌△ACD,
∴∠ABD=∠ACD,
在Rt△DBM和Rt△DCN中,
,
∴△DBM≌△DCN.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
