第一单元 平移、旋转与轴对称 单元复习卷 (含答案)苏教版四年级数学下册
文档属性
| 名称 | 第一单元 平移、旋转与轴对称 单元复习卷 (含答案)苏教版四年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 361.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 21:00:21 | ||
图片预览



文档简介
第一单元 平移、旋转与轴对称 单元复习卷 苏教版四年级数学下册
一、单选题
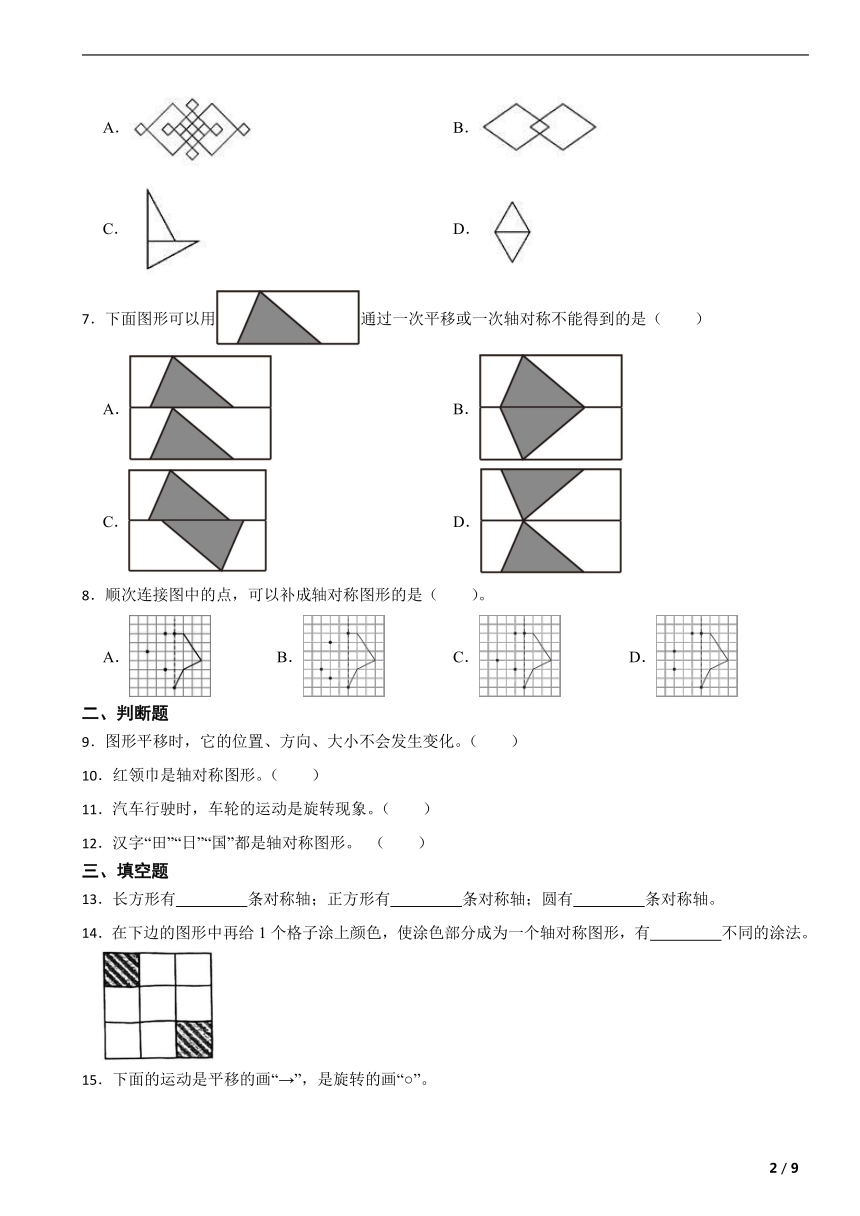
1.下面是一些图案,其中图案是轴对称图形的是( )。
A. B.
C. D.
2.角、线段、直角三角形、等边三角形、长方形,其中一定是轴对称图形的有( )个。
A.2个 B.3个 C.4个 D.5个
3.下面现象属于旋转的是( )。
A.分针的走动 B.电梯升降 C.拉抽屉 D.升国旗
4.旋转、平移、轴对称这三种图形的变换方法的相同点是( )。
A.都是沿一定的方向移动了一定的距离
B.都不改变图形的形状和大小
C.对应线段互相平行
5.把一张正方形纸片如图①、图②对折两次后,如图③再挖去一个三角形小孔,则展开后图形是( )。
A. B.
C. D.
6.下面的图案是由一个基本图形经过平移得到的是( )。
A. B.
C. D.
7.下面图形可以用通过一次平移或一次轴对称不能得到的是( )
A. B.
C. D.
8.顺次连接图中的点,可以补成轴对称图形的是( )。
A. B. C. D.
二、判断题
9.图形平移时,它的位置、方向、大小不会发生变化。( )
10.红领巾是轴对称图形。( )
11.汽车行驶时,车轮的运动是旋转现象。( )
12.汉字“田”“日”“国”都是轴对称图形。 ( )
三、填空题
13.长方形有 条对称轴;正方形有 条对称轴;圆有 条对称轴。
14.在下边的图形中再给1个格子涂上颜色,使涂色部分成为一个轴对称图形,有 不同的涂法。
15.下面的运动是平移的画“→”,是旋转的画“○”。
16.在溜冰时,人的前行是 现象,溜冰鞋底下的轮子运动是 现象。(填“旋转”或“平移”)
17.如图,可以通过平移变换但不能通过旋转变换得到的图案有 ;可以通过旋转变换但不能通过平移变换得到的图案有 ;既可通过平移变换,又可通过旋转变换得到的图案有 。
①②③④
18. 如图,一个大正方形被分成16个大小相同的小正方形,其中四个小正方形已涂成阴影,若再将一个小正方形涂成阴影,使所有阴影区域构成轴对称图形,则这个小正方形的编号为 。
四、解决问题
19.从镜子中看到一串数字是 ,这串数字实际是多少?
20.请用简洁的话描述①到②的运动轨迹以及①到③的运动轨迹
21.如图,1个大正方形被分成16个大小相同的小正方形,其中4个小正方形已涂上阴影,若再将一个小正方形涂上阴影,使所有阴影区域构成轴对称图形,则这个小正方形的编号为多少?
22.轮子向前滚动时,点e正好和1重合,点f和2重合,点g和3重合……
(1)在第一圈内,下面的字母对应的数分别是多少?
a→□
c→□
h→□
(2)点e会与10重合吗?点h会与12重合吗?
答案解析部分
1.【答案】C
【解析】【解答】解:选项A,不是轴对称图形;
选项B,不是轴对称图形;
选项C,是轴对称图形;
选项D,不是轴对称图形。
故答案为:C。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠。
2.【答案】C
【解析】【解答】解:角、线段、等边三角形、长方形都是轴对称图形,有4个。
故答案为:C。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
3.【答案】A
【解析】【解答】解:A项:分针的走动是旋转现象;
B项:电梯升降是平移现象;
C项:拉抽屉是平移现象;
D项:升国旗是平移现象。
故答案为:A。
【分析】比如像在平面上推东西、开关抽屉······这些物体都是沿着直线移动,这样的现象叫做平移;像转动方向盘、电扇的转动、旋转木马······这些物体都是绕着一个点或一个轴移动,这样的现象我们把它叫做旋转。
4.【答案】B
【解析】【解答】解:旋转、平移、轴对称这三种图形的变换方法的相同点是:都不改变图形的形状和大小。
故答案为:B。
【分析】旋转、平移、轴对称后物体的形状和大小不变,只是位置发生了变化。
5.【答案】C
【解析】【解答】解:三角形小孔的顶点对应的是正方形的边长,所以展开后的图形是。
故答案为:C。
【分析】正方形按对角线对折两次,被分成四个相等的三角形,挖去的小三角形会同时出现在四个相等的三角形上。
6.【答案】B
【解析】【解答】解:根据平移的特征可知,B图中的图形是一个基本图形平移得到的。
故答案为:B
【分析】平移后的图形的大小、形状、方向都不变,只是位置变化了,由此判断并形状即可。
7.【答案】C
【解析】【解答】解:A项:向下平移后得到;
B项:与原来的图形是轴对称图形;
C项:通过一次平移或一次轴对称不能得到;
D项:绕着三角形上面的顶点顺时针旋转180°得到。
故答案为:C。
【分析】依据轴对称、平移、旋转的知识画一画,想一想。
8.【答案】C
【解析】【解答】解:顺次连接图中的点,C形成的图形的是,是轴对称图形。
故答案为:C。
【分析】在轴对称图形中,对称轴两侧相对应的点到对称轴的距离相等。
9.【答案】错误
【解析】【解答】解:图形平移时,它的位置改变、形状大小不会发生变化,原题干说法错误。
故答案为:错误。
【分析】平移是指在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移;图形平移时,它的位置改变、形状大小不会发生变化。
10.【答案】正确
【解析】【解答】解:红领巾是轴对称图形。原题说法正确。
故答案为:正确。
【分析】一个图形沿着一条直线对折后两边能完全重合,这个图形就是轴对称图形,折痕所在的直线就是对称轴。
11.【答案】正确
【解析】【解答】解:行驶中的汽车车轮是旋转运动,这种运动形式也被称为旋转现象。原题说法正确。
故答案为:正确。
【分析】旋转是物体或图形绕某定点沿某方向移动;特点:图形的形状、大小不变,位置改变。
12.【答案】错误
【解析】【解答】解:汉字“田”“日”是轴对称图形,但是“国”不是轴对称图形。
故答案为:错误。
【分析】平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是轴对称图形。
13.【答案】2;4;无数
【解析】【解答】长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。故答案为:2;4;无数。
【分析】长方形长与宽的垂直平分线是它的对称轴; 正方形对边中点连线、对角线所在直线都是它的对称轴; 圆的直径就是对称轴。
14.【答案】3种
【解析】【解答】解:,有3种不同的涂法。
故答案为:3种。
【分析】依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴。
15.【答案】→;○;→;○
【解析】【解答】平移;
旋转;
平移;
旋转。
故答案为:→;○;→;○。
【分析】旋转和平移都是物体运动现象,都是沿某个方向作运动,运动中都没有改变本身的形状、大小与自身性质特征;区别:平移是物体或图形在同一平面内沿直线运动,朝某个方向移动一定的距离;旋转是绕一个定点沿某个方向旋转了一定的角度,旋转改变了图形的位置和方向。
16.【答案】平移;旋转
【解析】【解答】解:在溜冰时,人的前行是平移现象,溜冰鞋底下的轮子运动是旋转现象。
故答案为:平移;旋转。
【分析】平移是物体沿着一条直线运动;旋转是物体绕着一个中心或一个轴做圆周运动。
17.【答案】③;①、④;②
【解析】【解答】解:可以通过平移变换但不能通过旋转变换得到的图案有③;可以通过旋转变换但不能通过平移变换得到的图案有①、④;既可通过平移变换,又可通过旋转变换得到的图案有②。
故答案为:③;①、④;②。
【分析】依据平移的性质、旋转的性质填空。
18.【答案】4号
【解析】【解答】解:观察图形,将4号小正方形涂成阴影,使所有阴影区域构成轴对称图形;
故答案为:4号。
【分析】根据轴对称图形的特点可知,对称轴为3、6、10处的连线,所以在4号处涂上阴影,可使所有阴影区域构成轴对称图形。
19.【答案】738416
【解析】【分析】镜中的物体和实际物体大小相同,只是左右和正反方向发生变化,镜中像的左,是实物的右.
当把一件物品立于镜前,在镜子中看到的是以镜面为对称轴的物品的对称图形.镜中的图形和实际物体的左右方向正好相反,镜中物体的左侧是实际物品的右侧,镜中的一串数字中,左一是实际数字的右一,左二是实际的右二……以此类推.每个数字都同样如此,左侧是实际图形的右侧.
20.【答案】①到②:①向下平移5格到②①到③:方案一 ①向下平移5格到②,再向右平移9格到③方案二 ①向右平移9格,再向下平移5格到③
【解析】【解答】寻找图形中的一个点为定点,将求图形的运动轨迹转变为求某一个特殊点的运动轨迹,这样可以更容易得出正确答案。如本题中可以以树的顶端为定点,关注树顶那一点的变化来求运动轨迹
【分析】熟练掌握平移的概念以及简单运用,尽量由面到点
21.【答案】解:如图:
这个小正方形的编号为 4。
【解析】【分析】 根据轴对称图形的特点可知,对称轴为大长方形的对角线:3、6、阴影区、10这几个数字区域的连线,所以在4号处涂上阴影,可使所有阴影区域构成轴对称图形。
22.【答案】(1)a→5
c→7
h→4
(2)答:点e不会与10重合不,点h会与12重合。
【解析】【分析】(1)轮子上的每一格对应于线段上的一个刻度,点e正好和1重合,点f和2重合,点g和3重合,所以可以找到规律,依次往后数即. 可知道,在第1圈内,点a与5重合,点c与7重合,点h与4重合。
(2)轮子向前滚动,以8个字母(或数字)为一组,不断重复滚下去,点e第一次和1重合,每隔8个数就和线段上的数字重合一次;所以在第2圈内点e不会与10重合,点h会与12重合。
1 / 1
一、单选题
1.下面是一些图案,其中图案是轴对称图形的是( )。
A. B.
C. D.
2.角、线段、直角三角形、等边三角形、长方形,其中一定是轴对称图形的有( )个。
A.2个 B.3个 C.4个 D.5个
3.下面现象属于旋转的是( )。
A.分针的走动 B.电梯升降 C.拉抽屉 D.升国旗
4.旋转、平移、轴对称这三种图形的变换方法的相同点是( )。
A.都是沿一定的方向移动了一定的距离
B.都不改变图形的形状和大小
C.对应线段互相平行
5.把一张正方形纸片如图①、图②对折两次后,如图③再挖去一个三角形小孔,则展开后图形是( )。
A. B.
C. D.
6.下面的图案是由一个基本图形经过平移得到的是( )。
A. B.
C. D.
7.下面图形可以用通过一次平移或一次轴对称不能得到的是( )
A. B.
C. D.
8.顺次连接图中的点,可以补成轴对称图形的是( )。
A. B. C. D.
二、判断题
9.图形平移时,它的位置、方向、大小不会发生变化。( )
10.红领巾是轴对称图形。( )
11.汽车行驶时,车轮的运动是旋转现象。( )
12.汉字“田”“日”“国”都是轴对称图形。 ( )
三、填空题
13.长方形有 条对称轴;正方形有 条对称轴;圆有 条对称轴。
14.在下边的图形中再给1个格子涂上颜色,使涂色部分成为一个轴对称图形,有 不同的涂法。
15.下面的运动是平移的画“→”,是旋转的画“○”。
16.在溜冰时,人的前行是 现象,溜冰鞋底下的轮子运动是 现象。(填“旋转”或“平移”)
17.如图,可以通过平移变换但不能通过旋转变换得到的图案有 ;可以通过旋转变换但不能通过平移变换得到的图案有 ;既可通过平移变换,又可通过旋转变换得到的图案有 。
①②③④
18. 如图,一个大正方形被分成16个大小相同的小正方形,其中四个小正方形已涂成阴影,若再将一个小正方形涂成阴影,使所有阴影区域构成轴对称图形,则这个小正方形的编号为 。
四、解决问题
19.从镜子中看到一串数字是 ,这串数字实际是多少?
20.请用简洁的话描述①到②的运动轨迹以及①到③的运动轨迹
21.如图,1个大正方形被分成16个大小相同的小正方形,其中4个小正方形已涂上阴影,若再将一个小正方形涂上阴影,使所有阴影区域构成轴对称图形,则这个小正方形的编号为多少?
22.轮子向前滚动时,点e正好和1重合,点f和2重合,点g和3重合……
(1)在第一圈内,下面的字母对应的数分别是多少?
a→□
c→□
h→□
(2)点e会与10重合吗?点h会与12重合吗?
答案解析部分
1.【答案】C
【解析】【解答】解:选项A,不是轴对称图形;
选项B,不是轴对称图形;
选项C,是轴对称图形;
选项D,不是轴对称图形。
故答案为:C。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠。
2.【答案】C
【解析】【解答】解:角、线段、等边三角形、长方形都是轴对称图形,有4个。
故答案为:C。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
3.【答案】A
【解析】【解答】解:A项:分针的走动是旋转现象;
B项:电梯升降是平移现象;
C项:拉抽屉是平移现象;
D项:升国旗是平移现象。
故答案为:A。
【分析】比如像在平面上推东西、开关抽屉······这些物体都是沿着直线移动,这样的现象叫做平移;像转动方向盘、电扇的转动、旋转木马······这些物体都是绕着一个点或一个轴移动,这样的现象我们把它叫做旋转。
4.【答案】B
【解析】【解答】解:旋转、平移、轴对称这三种图形的变换方法的相同点是:都不改变图形的形状和大小。
故答案为:B。
【分析】旋转、平移、轴对称后物体的形状和大小不变,只是位置发生了变化。
5.【答案】C
【解析】【解答】解:三角形小孔的顶点对应的是正方形的边长,所以展开后的图形是。
故答案为:C。
【分析】正方形按对角线对折两次,被分成四个相等的三角形,挖去的小三角形会同时出现在四个相等的三角形上。
6.【答案】B
【解析】【解答】解:根据平移的特征可知,B图中的图形是一个基本图形平移得到的。
故答案为:B
【分析】平移后的图形的大小、形状、方向都不变,只是位置变化了,由此判断并形状即可。
7.【答案】C
【解析】【解答】解:A项:向下平移后得到;
B项:与原来的图形是轴对称图形;
C项:通过一次平移或一次轴对称不能得到;
D项:绕着三角形上面的顶点顺时针旋转180°得到。
故答案为:C。
【分析】依据轴对称、平移、旋转的知识画一画,想一想。
8.【答案】C
【解析】【解答】解:顺次连接图中的点,C形成的图形的是,是轴对称图形。
故答案为:C。
【分析】在轴对称图形中,对称轴两侧相对应的点到对称轴的距离相等。
9.【答案】错误
【解析】【解答】解:图形平移时,它的位置改变、形状大小不会发生变化,原题干说法错误。
故答案为:错误。
【分析】平移是指在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移;图形平移时,它的位置改变、形状大小不会发生变化。
10.【答案】正确
【解析】【解答】解:红领巾是轴对称图形。原题说法正确。
故答案为:正确。
【分析】一个图形沿着一条直线对折后两边能完全重合,这个图形就是轴对称图形,折痕所在的直线就是对称轴。
11.【答案】正确
【解析】【解答】解:行驶中的汽车车轮是旋转运动,这种运动形式也被称为旋转现象。原题说法正确。
故答案为:正确。
【分析】旋转是物体或图形绕某定点沿某方向移动;特点:图形的形状、大小不变,位置改变。
12.【答案】错误
【解析】【解答】解:汉字“田”“日”是轴对称图形,但是“国”不是轴对称图形。
故答案为:错误。
【分析】平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是轴对称图形。
13.【答案】2;4;无数
【解析】【解答】长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。故答案为:2;4;无数。
【分析】长方形长与宽的垂直平分线是它的对称轴; 正方形对边中点连线、对角线所在直线都是它的对称轴; 圆的直径就是对称轴。
14.【答案】3种
【解析】【解答】解:,有3种不同的涂法。
故答案为:3种。
【分析】依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴。
15.【答案】→;○;→;○
【解析】【解答】平移;
旋转;
平移;
旋转。
故答案为:→;○;→;○。
【分析】旋转和平移都是物体运动现象,都是沿某个方向作运动,运动中都没有改变本身的形状、大小与自身性质特征;区别:平移是物体或图形在同一平面内沿直线运动,朝某个方向移动一定的距离;旋转是绕一个定点沿某个方向旋转了一定的角度,旋转改变了图形的位置和方向。
16.【答案】平移;旋转
【解析】【解答】解:在溜冰时,人的前行是平移现象,溜冰鞋底下的轮子运动是旋转现象。
故答案为:平移;旋转。
【分析】平移是物体沿着一条直线运动;旋转是物体绕着一个中心或一个轴做圆周运动。
17.【答案】③;①、④;②
【解析】【解答】解:可以通过平移变换但不能通过旋转变换得到的图案有③;可以通过旋转变换但不能通过平移变换得到的图案有①、④;既可通过平移变换,又可通过旋转变换得到的图案有②。
故答案为:③;①、④;②。
【分析】依据平移的性质、旋转的性质填空。
18.【答案】4号
【解析】【解答】解:观察图形,将4号小正方形涂成阴影,使所有阴影区域构成轴对称图形;
故答案为:4号。
【分析】根据轴对称图形的特点可知,对称轴为3、6、10处的连线,所以在4号处涂上阴影,可使所有阴影区域构成轴对称图形。
19.【答案】738416
【解析】【分析】镜中的物体和实际物体大小相同,只是左右和正反方向发生变化,镜中像的左,是实物的右.
当把一件物品立于镜前,在镜子中看到的是以镜面为对称轴的物品的对称图形.镜中的图形和实际物体的左右方向正好相反,镜中物体的左侧是实际物品的右侧,镜中的一串数字中,左一是实际数字的右一,左二是实际的右二……以此类推.每个数字都同样如此,左侧是实际图形的右侧.
20.【答案】①到②:①向下平移5格到②①到③:方案一 ①向下平移5格到②,再向右平移9格到③方案二 ①向右平移9格,再向下平移5格到③
【解析】【解答】寻找图形中的一个点为定点,将求图形的运动轨迹转变为求某一个特殊点的运动轨迹,这样可以更容易得出正确答案。如本题中可以以树的顶端为定点,关注树顶那一点的变化来求运动轨迹
【分析】熟练掌握平移的概念以及简单运用,尽量由面到点
21.【答案】解:如图:
这个小正方形的编号为 4。
【解析】【分析】 根据轴对称图形的特点可知,对称轴为大长方形的对角线:3、6、阴影区、10这几个数字区域的连线,所以在4号处涂上阴影,可使所有阴影区域构成轴对称图形。
22.【答案】(1)a→5
c→7
h→4
(2)答:点e不会与10重合不,点h会与12重合。
【解析】【分析】(1)轮子上的每一格对应于线段上的一个刻度,点e正好和1重合,点f和2重合,点g和3重合,所以可以找到规律,依次往后数即. 可知道,在第1圈内,点a与5重合,点c与7重合,点h与4重合。
(2)轮子向前滚动,以8个字母(或数字)为一组,不断重复滚下去,点e第一次和1重合,每隔8个数就和线段上的数字重合一次;所以在第2圈内点e不会与10重合,点h会与12重合。
1 / 1
