六年级下册数学人教版比例 例1例2例3课件(共28张PPT)
文档属性
| 名称 | 六年级下册数学人教版比例 例1例2例3课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 21:42:57 | ||
图片预览


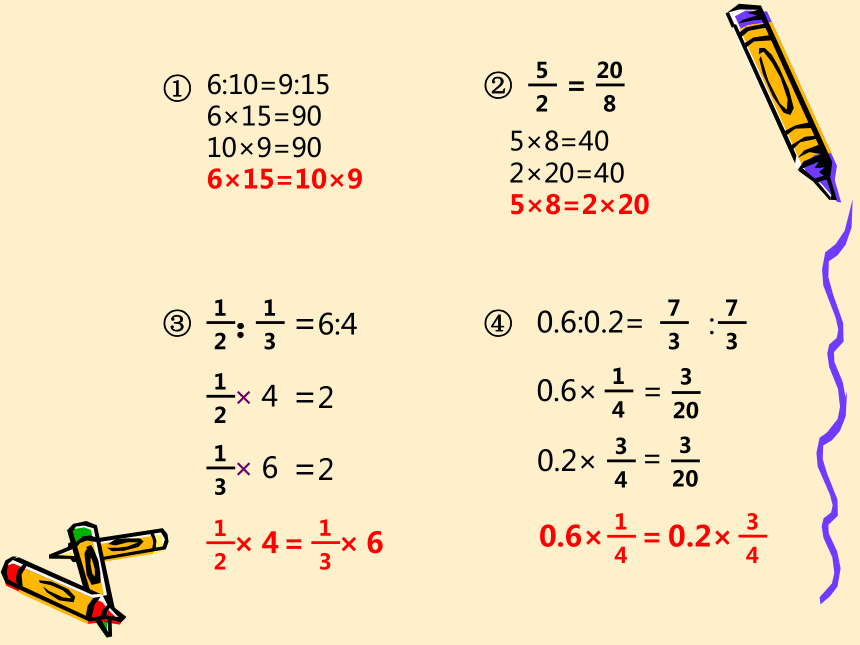



文档简介
(共28张PPT)
人教版数学六年级下册第四单元
比 例
比例的基本性质 例1
解比例 例2、例3
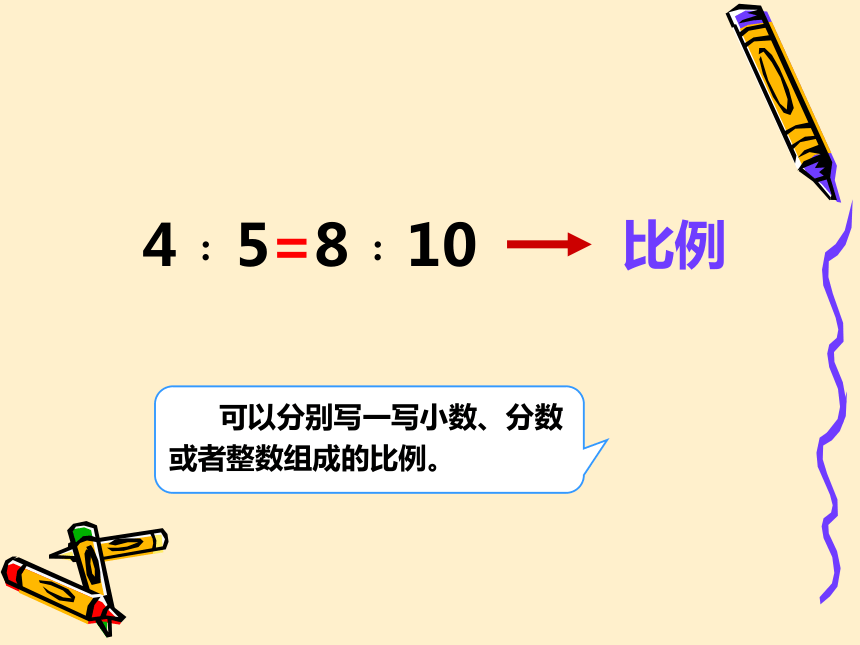
4﹕5=8﹕10
比例
可以分别写一写小数、分数或者整数组成的比例。
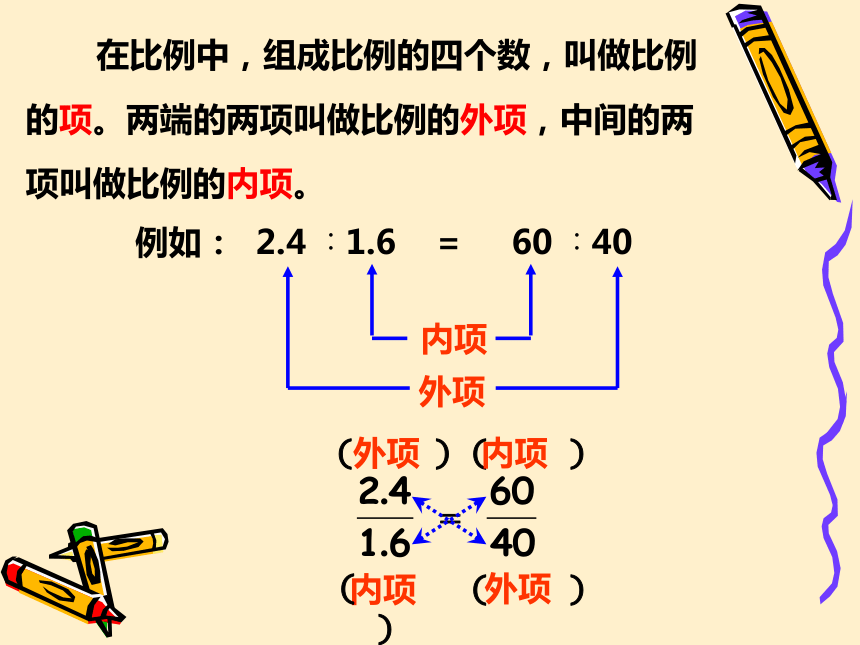
例如: 2.4 ∶1.6 = 60 ∶40
内项
外项
在比例中,组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
( )
内项
( )
( )
( )
外项
外项
内项
2.4 ∶1.6 = 60 ∶40
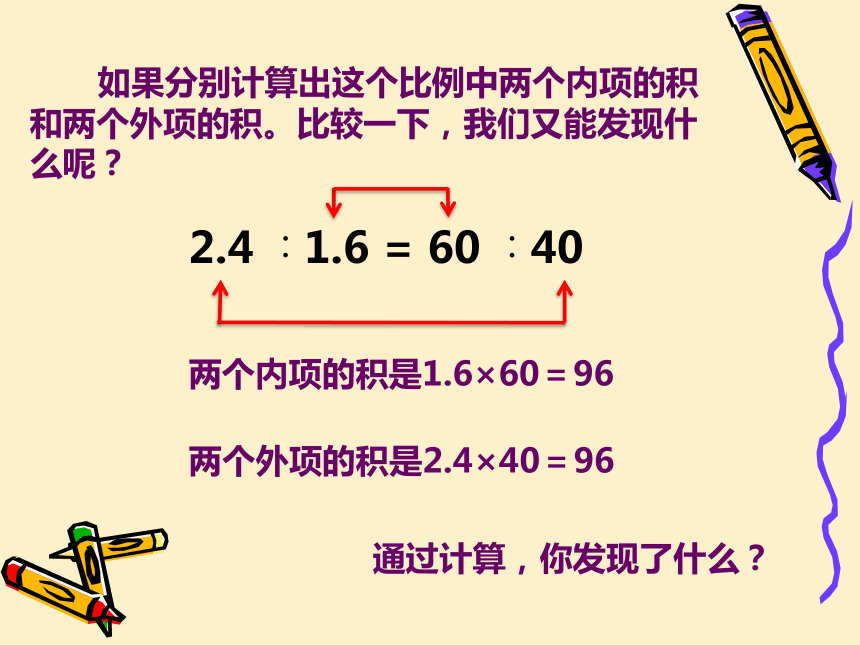
如果分别计算出这个比例中两个内项的积和两个外项的积。比较一下,我们又能发现什么呢?
两个外项的积是2.4×40=96
两个内项的积是1.6×60=96
通过计算,你发现了什么?
两个外项的积等于两个内项的积。
①
6:10=9:15
6×15=90
10×9=90
6×15=10×9
②
8
20
=
2
5
5×8=40
2×20=40
5×8=2×20
③
3
1
2
1
:
=6:4
2
1
×
4
=2
3
1
×
6
=2
2
1
×
4
3
1
×
6
=
④
3
7
0.6:0.2=
3
7
:
0.6×
4
1
=
20
3
0.2×
4
3
=
20
3
0.6×
4
1
0.2×
4
3
=
在比例中,两个外项的积等于两个内项的积。
比例的基本性质
你能用字母表示比例的基本性质吗?
如果 a :b = c ∶d(b、d≠0),
如果把比例写成分数形式 =
怎么相乘呢?
a
b
c
d
a
b
c
d
=
(交叉相乘)
那么 a d = b c。
a d = b c
应用比例的基本性质,判断下面两个比能不能组成比例。
0.2∶2.5 和 4∶50
因为, 0.2 × 50 = 10
2.5 × 4 = 10
10 = 10
所以,0.2∶2.5 和 4∶50
能组成比例。
试一试
因为,
所以,
判断
(1)在比例中,两个外项的积减去两个
内项的积,差是0。( )
(2)如果4:X=3:Y,(X和Y均不为0),
那么4X=3Y。( )
(3)因为3×10=5×6,所以3:5=10:6。( )
√
×
×
(1)在a:7=9:b中,( )和( )是内项,( )和( )是外项,ab=( )。
(2)一个比例的两个内项分别是3和8,则两个外项的积是( ),两个外项可能是( )和( )。
63
24
填一填
7
9
b
a
24
1
(3)在一个比例里,两个外项互为倒数,那么两个内项的积是( ),如果一个内项是 ,另一个内项是( )。
(4)在比例里,两个内项的积是18,其中一个外项是2,另一个外项是( )。
9
填一填
1
3
7
内项
2.4∶1.6=60∶40
外项
练习
(1)快速说出下列比例的外项和内项
外项
外项
内项
内项
2.4
1.6
60
40
=
练习
(2)应用比例的基本性质,判断下面哪组
中的两个比可以组成比例。
6∶3和8∶5
0.6∶0.2和 ∶
3
4
—
4
1
—
6×5=30
3×8=24
不能组成比例
可以组成比例
4
1
—
0.6× =0.15
0.2× =0.15
3
4
—
0.6∶0.2= ∶
3
4
—
4
1
—
练习
(3)说出下面比例中缺少的项是几?
14∶21=2∶( )
3
14
21
=
2
3
比例的意义
比例的基本性质
21×2=42
14×( )=42
求比例中的未知项,叫做解比例。
法国巴黎的埃菲尔铁塔高度约320m,北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1∶10。这座模型高多少米?
模型的高度∶原塔的高度=1∶10
320
未知项
x
法国巴黎的埃菲尔铁塔高度约320m,北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米?
x∶320=1∶10
x=
320÷10
x=32
答:这座模型高32m。
解:设这座模型高x m。
外项
内项
10x=320×1
x=32
答:这座模型高32m。
x=
320×1
10
1
32
x∶320=1∶10
找
设
列
转
解
答
10x=320×1
10x=320
解比例
2.4
1.5
6
x
—
=
1. 别忘记先写“解”字
2.一般把含有x的式子写在等号的左边。
检验:
1.比例的意义
1.5
2.4÷
=1.6
6÷
4
15
=1.6
1.6=1.6
2.比例的基本性质
2.4×
4
15
=9
1.6×5=9
9=9
巩固练习:
0.4∶x=1.2∶2
x ∶10= ∶
3
x
=
12
2.4
解:
x=
解:
1.2x=0.4×2
1.2x=0.8
x=0.8÷1.2
解:
12x=2.4×3
12x=7.2
x=7.2÷12
0.6
10×
1
4
1
3
x=
x=
1
3
5
2
2
3
4
1
3
1
3
1
内项
内项
外项
外项
交叉相乘
1.解比例
2
5
2
15
x=
x=
÷
x=
(1)
x
8.5
8
4
=
解:8x=8.5×4
8x=34
x=34÷8
x=4.25( )
×
错误改正:
x
8.5
8
4
=
解:4x=8×8.5
4x=68
x=68÷4
x=17
巩固练习:
2.判断
(2)
x
25
1.2
2
=
解:2x=25×1.2
x=
( )
×
25×1.2
2
6
1
错误改正:
=
解:2x=25×1.2
x=
x=15
25×1.2
2
0.6
1
x
25
1.2
2
x=150
解决问题:
(1)如果有525 g水,要配制
这种农药,需要放进多少
克的药?
配制一种农药,其中药与水的质量比为1∶150。
(2)如果有3 g药,需要准备
多少克水?
解:设需要放进x 克的药。
x∶525= 1∶150
150x=525×1
x=3.5
答:需要放进3.5 克药。
解:设需要准备x 克水。
3∶x = 1∶150
1×x=3×150
x=450
答:需要准备450克水。
150x=525
1.根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
我的收获:
2.解比例的方法:先根据比例的基本性质将比例转化为乘积形式,再通过解方程求出未知项的值。
3.解决问题6部曲:
找—设—列—转—解—答。
课后练习:
请你用3、9、18、x这四个数组成比例,并解比例,试试你最多能写出几个?
同学们,再见!
已知24×3=8×9,你能写出比例吗?你能写几个?写完之后问问老师,写的对不对。
课后思考
人教版数学六年级下册第四单元
比 例
比例的基本性质 例1
解比例 例2、例3
4﹕5=8﹕10
比例
可以分别写一写小数、分数或者整数组成的比例。
例如: 2.4 ∶1.6 = 60 ∶40
内项
外项
在比例中,组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
( )
内项
( )
( )
( )
外项
外项
内项
2.4 ∶1.6 = 60 ∶40
如果分别计算出这个比例中两个内项的积和两个外项的积。比较一下,我们又能发现什么呢?
两个外项的积是2.4×40=96
两个内项的积是1.6×60=96
通过计算,你发现了什么?
两个外项的积等于两个内项的积。
①
6:10=9:15
6×15=90
10×9=90
6×15=10×9
②
8
20
=
2
5
5×8=40
2×20=40
5×8=2×20
③
3
1
2
1
:
=6:4
2
1
×
4
=2
3
1
×
6
=2
2
1
×
4
3
1
×
6
=
④
3
7
0.6:0.2=
3
7
:
0.6×
4
1
=
20
3
0.2×
4
3
=
20
3
0.6×
4
1
0.2×
4
3
=
在比例中,两个外项的积等于两个内项的积。
比例的基本性质
你能用字母表示比例的基本性质吗?
如果 a :b = c ∶d(b、d≠0),
如果把比例写成分数形式 =
怎么相乘呢?
a
b
c
d
a
b
c
d
=
(交叉相乘)
那么 a d = b c。
a d = b c
应用比例的基本性质,判断下面两个比能不能组成比例。
0.2∶2.5 和 4∶50
因为, 0.2 × 50 = 10
2.5 × 4 = 10
10 = 10
所以,0.2∶2.5 和 4∶50
能组成比例。
试一试
因为,
所以,
判断
(1)在比例中,两个外项的积减去两个
内项的积,差是0。( )
(2)如果4:X=3:Y,(X和Y均不为0),
那么4X=3Y。( )
(3)因为3×10=5×6,所以3:5=10:6。( )
√
×
×
(1)在a:7=9:b中,( )和( )是内项,( )和( )是外项,ab=( )。
(2)一个比例的两个内项分别是3和8,则两个外项的积是( ),两个外项可能是( )和( )。
63
24
填一填
7
9
b
a
24
1
(3)在一个比例里,两个外项互为倒数,那么两个内项的积是( ),如果一个内项是 ,另一个内项是( )。
(4)在比例里,两个内项的积是18,其中一个外项是2,另一个外项是( )。
9
填一填
1
3
7
内项
2.4∶1.6=60∶40
外项
练习
(1)快速说出下列比例的外项和内项
外项
外项
内项
内项
2.4
1.6
60
40
=
练习
(2)应用比例的基本性质,判断下面哪组
中的两个比可以组成比例。
6∶3和8∶5
0.6∶0.2和 ∶
3
4
—
4
1
—
6×5=30
3×8=24
不能组成比例
可以组成比例
4
1
—
0.6× =0.15
0.2× =0.15
3
4
—
0.6∶0.2= ∶
3
4
—
4
1
—
练习
(3)说出下面比例中缺少的项是几?
14∶21=2∶( )
3
14
21
=
2
3
比例的意义
比例的基本性质
21×2=42
14×( )=42
求比例中的未知项,叫做解比例。
法国巴黎的埃菲尔铁塔高度约320m,北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1∶10。这座模型高多少米?
模型的高度∶原塔的高度=1∶10
320
未知项
x
法国巴黎的埃菲尔铁塔高度约320m,北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米?
x∶320=1∶10
x=
320÷10
x=32
答:这座模型高32m。
解:设这座模型高x m。
外项
内项
10x=320×1
x=32
答:这座模型高32m。
x=
320×1
10
1
32
x∶320=1∶10
找
设
列
转
解
答
10x=320×1
10x=320
解比例
2.4
1.5
6
x
—
=
1. 别忘记先写“解”字
2.一般把含有x的式子写在等号的左边。
检验:
1.比例的意义
1.5
2.4÷
=1.6
6÷
4
15
=1.6
1.6=1.6
2.比例的基本性质
2.4×
4
15
=9
1.6×5=9
9=9
巩固练习:
0.4∶x=1.2∶2
x ∶10= ∶
3
x
=
12
2.4
解:
x=
解:
1.2x=0.4×2
1.2x=0.8
x=0.8÷1.2
解:
12x=2.4×3
12x=7.2
x=7.2÷12
0.6
10×
1
4
1
3
x=
x=
1
3
5
2
2
3
4
1
3
1
3
1
内项
内项
外项
外项
交叉相乘
1.解比例
2
5
2
15
x=
x=
÷
x=
(1)
x
8.5
8
4
=
解:8x=8.5×4
8x=34
x=34÷8
x=4.25( )
×
错误改正:
x
8.5
8
4
=
解:4x=8×8.5
4x=68
x=68÷4
x=17
巩固练习:
2.判断
(2)
x
25
1.2
2
=
解:2x=25×1.2
x=
( )
×
25×1.2
2
6
1
错误改正:
=
解:2x=25×1.2
x=
x=15
25×1.2
2
0.6
1
x
25
1.2
2
x=150
解决问题:
(1)如果有525 g水,要配制
这种农药,需要放进多少
克的药?
配制一种农药,其中药与水的质量比为1∶150。
(2)如果有3 g药,需要准备
多少克水?
解:设需要放进x 克的药。
x∶525= 1∶150
150x=525×1
x=3.5
答:需要放进3.5 克药。
解:设需要准备x 克水。
3∶x = 1∶150
1×x=3×150
x=450
答:需要准备450克水。
150x=525
1.根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
我的收获:
2.解比例的方法:先根据比例的基本性质将比例转化为乘积形式,再通过解方程求出未知项的值。
3.解决问题6部曲:
找—设—列—转—解—答。
课后练习:
请你用3、9、18、x这四个数组成比例,并解比例,试试你最多能写出几个?
同学们,再见!
已知24×3=8×9,你能写出比例吗?你能写几个?写完之后问问老师,写的对不对。
课后思考
