第一章 三角形的证明 素养提优卷(含解析)
文档属性
| 名称 | 第一章 三角形的证明 素养提优卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 786.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 00:00:00 | ||
图片预览



文档简介
第一章 三角形的证明 素养提优卷
考试分数:120分 考试时间:100分钟
一、单选题(本大题共10小题,共30分)
1.如图,屋顶钢架外框是等腰三角形,其中,工人师傅在焊接立柱时,只用找到的中点D,这就可以说明竖梁垂直于横梁了,工人师傅这种操作方法的依据是( )
A.等边对等角 B.等角对等 C.垂线段最短 D.等腰三角形“三线合一”
第1题图 第2题图 第3题图
2.如图,在直角三角形中,,作图痕迹如图所示,若,,则的面积是( )
A.1 B. C.2 D.
3.如图,点在线段上,点在线段上,且和均是等边三角形,那么( )
A. B. C. D.
4.校园湖边一角的形状如图所示,其中,,表示围墙,若在线段右侧的区域中找到一点P修建一个观赏亭,使点P到三面墙的距离都相等,则点P在( )
A.线段、的交点 B.、角平分线的交点
C.线段、垂直平分线的交点 D.线段、垂直平分线的交点
5.如图,在中,,要求在上找一点,使将分成两个等腰三角形. 现有如下两种设计方案,下列说法正确的是( )
方案一:作的平分线,使其交于点;
方案二:作的垂直平分线,使其交于点
A.两种方案都正确 B.只有方案一正确
C.只有方案二正确 D.两种方案都不正确
第5题图 第6题图 第7题图
6.如图所示,点O在点A的正北方,相距千米,,.则点B相对于点A的位置可以表示为( )
A.点B在点A的南偏东,距离20千米
B.点B在点A的南偏东,距离40千米
C.点B在点A的北偏西,距离40千米
D.点B在点A的北偏西,距离20千米
7.“八一薪火相传,七秩桃李芬芳”,今年是我校建校七十周年,为传承学校优良传统和红色基因,展示自建校以来各历史时期的文档资料和实物,学校将校本部的“大白楼”布置为校史馆。如图1所示为“大白楼”的正门,它的顶部可以看作如图2所示的等腰三角形,已知米,米,则的面积为( )平方米.
A.40 B.24 C.20 D.12
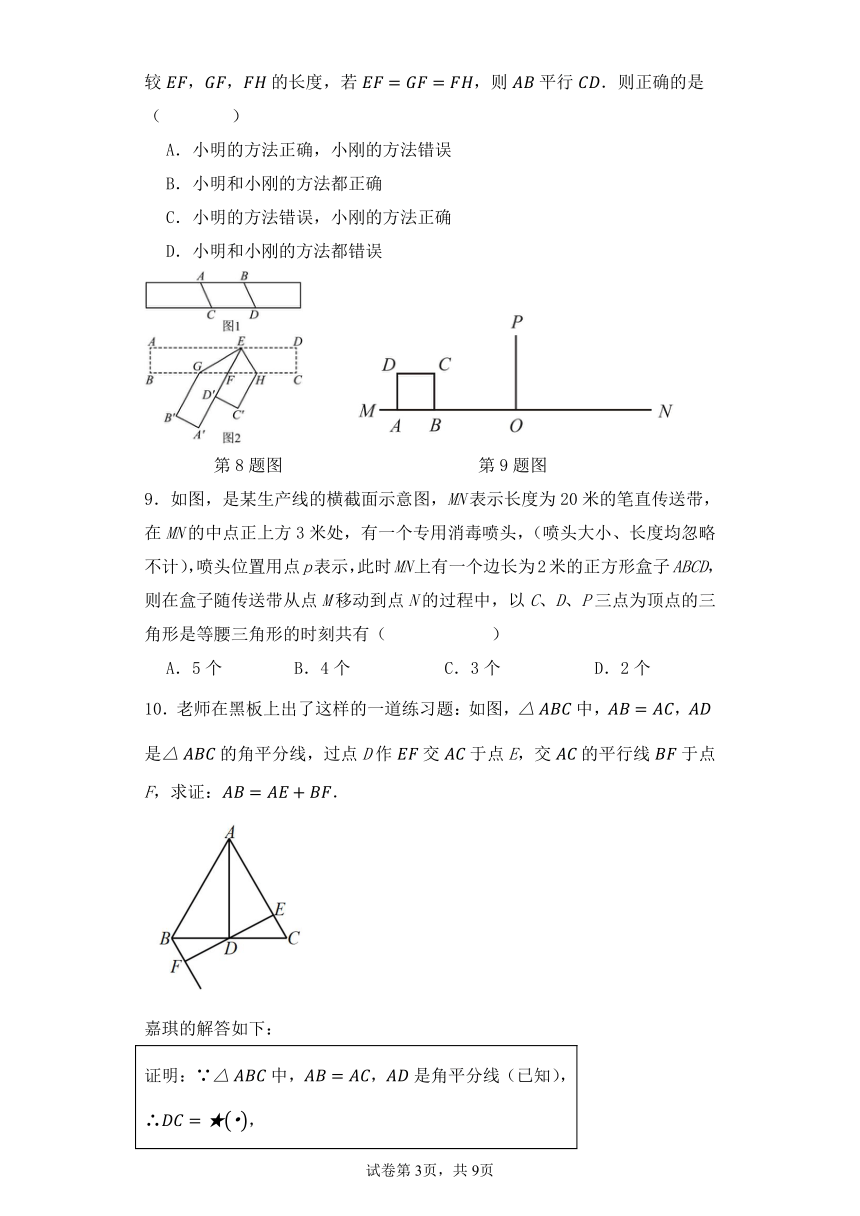
8.只用圆规来验证纸片的两边是否平行的探究活动中,小明的方法是:在纸片的一边上取线段,用圆规在另一边上截取,使,如图1.用圆规比较和的长度,若相同则平行.小刚的方法是:折叠纸条,使和重合,交于点F,折痕为和,如图2.用圆规比较,,的长度,若,则平行.则正确的是( )
A.小明的方法正确,小刚的方法错误
B.小明和小刚的方法都正确
C.小明的方法错误,小刚的方法正确
D.小明和小刚的方法都错误
第8题图 第9题图
9.如图,是某生产线的横截面示意图,MN表示长度为20米的笔直传送带,在MN的中点正上方3米处,有一个专用消毒喷头,(喷头大小、长度均忽略不计),喷头位置用点p表示,此时MN上有一个边长为2米的正方形盒子ABCD,则在盒子随传送带从点M移动到点N的过程中,以C、D、P三点为顶点的三角形是等腰三角形的时刻共有( )
A.5个 B.4个 C.3个 D.2个
10.老师在黑板上出了这样的一道练习题:如图,中,,是的角平分线,过点D作交于点E,交的平行线于点F,求证:.
嘉琪的解答如下:
证明:∵中,,是角平分线(已知), ∴, ∵(已知), ∴(两直线平行,内错角相等) 又∵(对顶角相等), ∴(▲), ∴(全等三角形对应边相等). ∴(等量代换).
下列选项错误的是( )
A.★表示 B.直接依据●表示等腰三角形“三线合一”
C.※表示 D.直接依据▲表示
二、填空题(本大题共5小题,共15分)
11.如图1,小明用尺规作出∠AOB的角平分线OC.为探索作图的道理,在图1中连接CE,CD得到图2,根据作法可得COE≌COD.他判定两个三角形全等的依据是
12.如图1,是某超市自动扶梯,如图2,是其的示意图,大厅两层之间的距离米,自动扶梯的倾角为30°,若自动扶梯运行速度米/秒,则顾客乘自动扶梯上一层楼的时间为 秒.
13.数学活动课上,志强用硬纸板剪了一个等腰三角形,但因失误同时剪掉该三角形的一个角,如图所示,经测量,,则被剪掉的的度数为 .
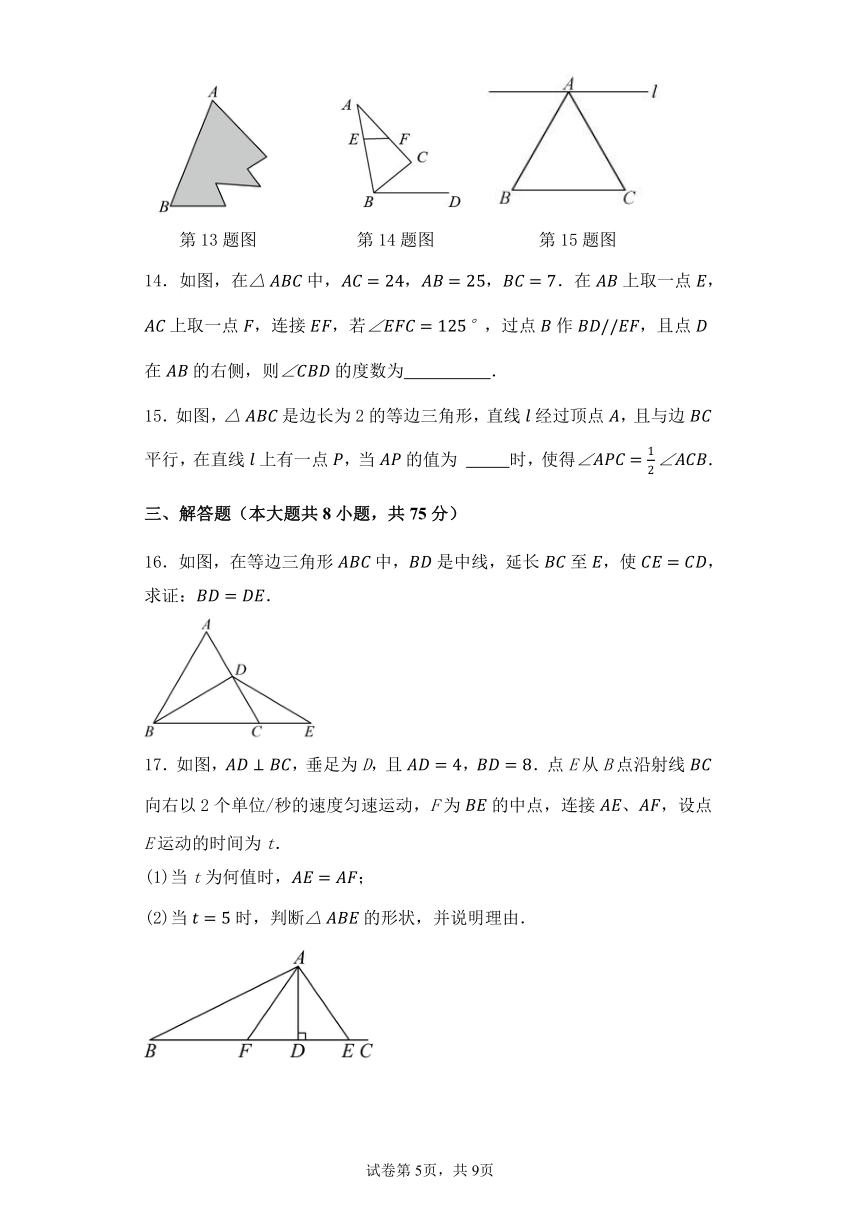
第13题图 第14题图 第15题图
14.如图,在中,,,.在上取一点,上取一点,连接,若,过点作,且点在的右侧,则的度数为 .
15.如图,是边长为2的等边三角形,直线经过顶点,且与边平行,在直线上有一点,当的值为 时,使得.
三、解答题(本大题共8小题,共75分)
16.如图,在等边三角形中,是中线,延长至,使,求证:.
17.如图,,垂足为D,且,.点E从B点沿射线向右以2个单位/秒的速度匀速运动,F为的中点,连接,设点E运动的时间为t.
(1)当t为何值时,;
(2)当时,判断的形状,并说明理由.
18.如图,,交于点F,点C在线段上,且,,,连接,.
(1)求证:;
(2)若,,求的度数.
19.如图,在中,,是过点A的直线,于D,于点E;
(1)若B、C在的同侧(如图1所示)且.求证:;
(2)若B、C在的两侧(如图2所示),且,其他条件不变,与仍垂直吗?若是请给出证明;若不是,请说明理由.
20.有一块等腰三角形木板,其中(如图),王师傅准备把它分成全等的两部分, 小明和小刚分别设计了两种方案:
(1)小明:确定BC的中点D,连结(如图1).
(2)小刚:作于D(如图2).
王师傅说两种办法都行,请选择一种说出其中的道理(写出已知、求证、证明).
21.某天,暴雨突然来袭,两艘搜救艇接到消息,在海面上有遇险船只从A、B两地发出求救信号.于是,第一艘搜救艇以20海里/时的速度离开港口O沿北偏东40°的方向向A地出发,同时,第二艘搜救艇也从港口O出发,以15海里/时的速度向B地出发,2小时后,他们同时到达各自的目标位置.此时,他们相距50海里.
(1)求第二艘搜救艇的航行方向是北偏西多少度?(求的大小)
(2)由于B地需要被援救的人数较多,故需要搭载人数较少的第一艘搜救艇改道去到B地支援,在从A地前往到B地的过程中,与港口O最近的距离是多少?
22.已知,是一条角平分线.
【探究发现】如图1,若是的角平分线.可得到结论:.
小红的解法如下:
过点D作于点E,于点F,过点A作于点G,
∵是的角平分线,且,
∴______.
∴______,
又∵,
∴______.
【类比探究】如图2,若是的外角平分线,与的延长线交于点D.
求证:
【拓展应用】如图3,在中,,分别是的角平分线且相交于点D,,直接写出的值是______.
23.综合与探究:
在综合实践课上,张老师首先出示了例题.
例题:在等腰三角形中.,求的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏同学编了如下一题:
变式:在等腰三角形中,,求的度数
(1)请你解答以上变式题;
(2)解(1)后,小敏发现,的度数不同,得到的度数的个数也可能不同,在等腰三角形中,设,当 有三个不同的度数时,请你探索的取值范围然后张老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动如图,在 中,,,将一块足够大的直角三角尺按如图所示位置放置,顶点在线段上滑动(点不与,重合),三角尺的直角边始终经过点 ,并且与 的夹角 ,斜边交于点
(3)小华发现在点的滑动过程中,的形状也在改变,请你探索可以是等腰三角形吗?若不可以,请说明理由;若可以,请求出的大小
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据等腰三角形的性质解答即可.
【详解】解:∵,,
∴,
故工人师傅这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
【点睛】本题考查等腰三角形的性质,熟知等腰三角形“三线合一”性质是解答的关键.
2.C
【分析】本题考查了角平分线的性质,过点作于点,根据作图可得是的角平分线,则,进而根据三角形的面积公式,即可求解.
【详解】解:如图所示,过点作于点,
根据作图可得是的角平分线,
又直角三角形中,,
∴
∴的面积是,
故选:C.
3.D
【分析】本题考查了等边三角形的性质、三角形内角和定理、平角的定义;由等边三角形的性质和平角的定义以及三角形内角和定理即可得出结果.
【详解】解:∵和均是等边三角形,
∴,
∵,,,
∴,
∵,
∴;
故选:D.
4.B
【分析】由角平分线的性质定理:角平分线上的点到角两边的距离相等,可判断为D.
【详解】解:如图,、角平分线的交点P,,,,垂足分别为K,L,M,则,即点P到三面墙的距离相等;
故选:B
【点睛】本题考查角平分线的性质定理;掌握角平分线的性质定理是解题的关键.
5.A
【分析】本题主要考查等腰三角形的性质与判定和垂直平分线的性质,对于两种方案均证明,可得结论.
【详解】解:方案一:如图1中,
∵
∴,
∵平分,
∴,
∴,
∴为等腰三角形,
∴,
∴为等腰三角形;
方案二:如图2,
∵
∴,
∵是边的垂直平分线,
∴
∴,
∴为等腰三角形,
∴,
∴为等腰三角形;
故选项A正确,
故选:A.
6.C
【分析】连接,得到等边,根据方位角的定义判断即可.
【详解】如图,连接,
∵,,
∴是等边三角形,
∴,
∴点B在点A的北偏西,距离40千米,
故选C.
【点睛】本题考查了等边三角形的判定和性质,方位角的应用,熟练掌握等边三角形的判定,方位角的意义是解题的关键.
7.D
【分析】过点A作,根据等腰三角形的定义可得为三角形的高,即可求得结果.
【详解】解:过点A作,如图所示:
∵米,
∴垂直平分,
∵米,
∴米,
根据勾股定理可得:米,
∴(平方米),
故答案选:D.
【点睛】本题考查了等腰三角形的性质,根据勾股定理求出高的长是解题的关键.
8.B
【分析】在图1中,连接,可证明,得,所以,可知小明的方法正确;在图2中,由,得,由折叠得,则,所以,可知小刚的方法正确,于是得到问题的答案.
【详解】解:如图1,连接,
在和中,,
∴,
∴,
∴,
∴小明的方法正确;
如图2,∵,
∴,
由折叠得,
∴,
∴,
∴小刚的方法正确,
故选:B.
【点睛】此题重点考查平行线的判定与性质、全等三角形的判定与性质、等腰三角形的性质等知识,证明两条直线被第三条直线所截得的内错角相等是解题的关键.
9.A
【分析】根据已知条件,利用等腰三角形的性质分情况讨论即可.
【详解】解:∵四边形为正方形
∴,
∵,在中点,
∴,
∴①当正方形在上,时,为等腰三角形;
②当正方形在 上,时,为等腰三角形;
③当过正方形边中点上时,,为等腰三角形;
④当正方形在上,时,为等腰三角形;
⑤当正方形在上,时,为等腰三角形;
综上所述,以、、三点为顶点的三角形是等腰三角形的时刻共有5个.
故选:.
【点睛】本题考查了等腰三角形的性质,正确理解题意、熟练掌握等腰三角形的性质是解题的关键.
10.D
【分析】根据等腰三角形的性质及全等三角形的性质与判定可进行求解.
【详解】证明:∵中,,是角平分线(已知),
∴(等腰三角形的“三线合一”),故A,B选项正确,不符合题意;
∵(已知),
∴(两直线平行,内错角相等)故C选项正确,不符合题意;
又∵(对顶角相等),
∴(),故D选项错误,符合题意;
∴(全等三角形对应边相等).
∴(等量代换);
故选D.
【点睛】本题主要考查等腰三角形的性质及全等三角形的性质与判定,熟练掌握等腰三角形的性质及全等三角形的性质与判定是解题的关键.
11.SSS
【分析】根据SSS证明三角形全等即可.
【详解】解:由作法可知:OE=OD,EC=DC,
在COE和COD中,
,
∴COE≌COD(SSS),
∴∠COE=∠COD,
∴OC平分∠AOB.
故答案为:SSS.
【点睛】本题考查作图-复杂作图,全等三角形的判定等知识,解题的关键是读懂图形中的信息,属于基础题型.
12.26
【分析】此题利用查直角三角形的性质求得自动扶梯的长,则顾客乘自动扶梯上一层楼的时间可求.
【详解】解:∵30°锐角所对直角边等于斜边的一半,
∴顾客乘自动扶梯上一层楼的距离为2h=13米,
∴顾客乘自动扶梯上一层楼的时间为13÷0.5=26秒.
【点睛】解决此类题目的关键是要熟记30°锐角所对直角边等于斜边的一半.注意数学在实际生活中的运用.
13.或或
【分析】分、、为顶角讨论即可求解.
【详解】解:当为顶角时,和为底角,
∵,
∴;
当为顶角时,和为底角,
∵,
∴;
当为顶角时,和为底角,
∵,
∴,
∴;
∴被剪掉的的度数为或或.
故答案为:或或.
【点睛】本题考查了等腰三角形的性质,三角形内角和定理等知识,明确题意,合理分类讨论,找出所求问题需要的条件是解题的关键.
14.
【分析】在中,由三边的长度可得出,进而可得出为直角三角形且,由于平行线之间有拐点,所以过点C作交AB于点M,则,利用平行的性质可得出的度数,结合可求出的度数,再利用“两直线平行,内错角相等”即可求出的度数.
【详解】解:在中,,,,
∵,即,
∴为直角三角形且.
过点C作交AB于点M,则,如下图所示,
∵,,
∴,
∴.
又∵,
∴.
故答案为:.
【点睛】本题考查了勾股定理的逆定理以及平行线的性质,利用勾股定理的逆定理,找出并知道过拐点作已知直线的平行线是解题的关键.
15.2或4/4或2
【分析】在直线上分别截取,连接,根据等边三角形的性质即可解决问题.
【详解】解:当或4时,使得,理由如下:
∵是边长为2的等边三角形,
∴,
如下图,在直线上分别截取,点为中点,连接,
∴,
∵直线经过顶点,且与边平行,
∴,
∴,
∴,
∴;
如图,连接,
∵,
∵,
∴是等边三角形,
∴,,
∴,
∴.
∴当AP的值为2或4时,使得.
故答案为:2或4.
【点睛】本题主要考查了作图—尺规作图、平行线的性质、等边三角形的判定与性质、等腰三角形的性质等知识,解题关键是灵活运用所学知识.
16.见解析
【分析】本题考查了等边三角形的性质,三角形外角的性质,等腰三角形的判定和性质;
根据等边三角形的性质求出,,然后根据三角形外角的性质和等边对等角求出,得到,再根据等角对等边得出结论.
【详解】证明:∵在等边三角形中,是中线,
∴,,
∵,
∴,
∴,
∴.
17.(1)当时,;
(2)是直角三角形,理由见解析
【分析】(1)根据题意可得:,再根据线段中点的定义可得,从而可得,,由等腰三角形的性质得,则建立方程即可解答;
(2)当时,,,然后分别在和中,利用勾股定理求出和,最后利用勾股定理的逆定理证明是直角三角形,即可解答.
【详解】(1)解:由题意得:,
∵F为的中点,
∴,
∵,,
∴,,
∵,,
∴,
即,
解得:,
∴当时,;
(2)解:是直角三角形,
理由:当时,,
∴,
在中,,
在中,,
∵,,
∴,
∴是直角三角形.
【点睛】本题考查了勾股定理,勾股定理的逆定理,等腰三角形的性质,熟练掌握勾股定理,以及勾股定理的逆定理是解题的关键.
18.(1)见解析
(2)
【分析】本题考查了全等三角形的判定和性质,平行线的性质,等腰三角形的性质,三角形外角性质.
(1)根据,可得,即可得证,从而得出结论;
(2)根据全等三角形的性质,可得,,根据三角形外角的性质,可得,根据等腰三角形的性质即可求出的度数.
【详解】(1)证明:,
,
在和中,
,
,
;
(2)解:,
,,
,
,
,
,
,
.
19.(1)见解析
(2),见解析
【分析】本题主要考查了三角形全等的判定和性质.
(1)通过证明,根据全等三角形对应角相等,即可求证;
(2)用和(1)相同的方法证明,根据全等三角形对应角相等,即可求证.
【详解】(1)证明:∵,,
∴,
在和中,
∵,
∴.
∴
∵,
∴.
∴.
∴.
(2)解:.理由如下:
∵,,
∴,
在和中,
∵,
∴.
∴,
∵,
∴,即,
∴.
20.选择(1),证明见解析,或选择(2),证明见解析
【分析】选择(1),通过证明即可.或选择(2),通过证明即可.
【详解】选择(1),
已知:△ABC中,,,
求证:,
证明:在和中,
∴
选择(2),
已知:△ABC中,,,
求证:,
证明:∵,
∴,
在和中,
∴
【点睛】本题考查了全等三角形的判定,解决本题的关键是熟练掌握全等三角形的判定.
21.(1)50度
(2)24海里
【分析】(1)根据题意求出OA、OB,根据勾股定理的逆定理推证出即得;
(2)根据垂线段定理即得.
【详解】(1)由题得:海里/时×2小时海里;海里/时×2小时海里,
∵,,
∴,
∴为直角三角形,
∴,
∵由题知,
∴,
即第二艘搜救艇的航行方向是北偏西50度.
(2)过点O作,此时OE的长度即为最近距离,
由(1)知,,,
∴在中,有,
即,
∴,
答:与港口O最近的距离是24海里.
【点睛】本题考查了勾股定理和其逆定理的应用,能熟练运用勾股定理及和其逆定理是解决本题的关键.
22.(1);;;(2)见解析;(3)
【分析】探究发现:根据题干中的解题思路求解即可;
类比探究:过点D作于N,过点D作于M.过点A作于点P.利用角平分线的性质及等面积法证明即可;
拓展应用:在BC上取点G,使得,连接,先利用全等三角形的判定得出再由其性质及前面的结论求解即可.
【详解】探究发现:解:过点D作于点E,于点F,过点A作于点G,
∵是的角平分线,且,
∴
∴,
又∵,
∴,
故答案为:,;;
类比探究:证明:过点D作于N,过点D作于.过点A作于点P.
∵平分,
∴.
∴,
∴
拓展应用:在BC上取点G,使得,连接,
∵分别是的角平分线且相交于点D,
∴,,
∵,
∴,
∴,
∴
∴是的角平分线
由(1)知,,
设,,则,
由(1)知,
.
【点睛】题目主要考查角平分线的性质及全等三角形的判定和性质,三角形等面积法等,理解题意,熟练掌握运算角平分线的性质是解题关键.
23.(1)或或;(2)当且时,有三个不同的度数;(3)是或或
【分析】(1)分三种情况:当为顶角时,当为顶角时,当为顶角时,利用等腰三角形两底角相等解答;
(2)分为两种情况:①当时,②当时,根据等腰三角形的性质求解;
(3)分三种情况,利用等腰三角形的性质,分别探究是等腰三角形的情况.
【详解】解:(1)∵,
当为顶角时,为底角,则;
当为顶角时,为底角,;
当为顶角时,为底角,;
(2)分为两种情况:
①当时,只能为顶角,
∴的度数只有一个;
②当时,
若为顶角,则;
若为底角,为顶角,则;
若为底角,为底角,则;
当且且,即时,有三个不同的度数,
综上所述,可知当且时,有三个不同的度数;
(3)的形状可以是等腰三角形,,
①当时,是等腰三角形,
∴ ,
即,解得;
②当时,是等腰三角形,
∴,
即,解得;
③当时,是等腰三角形,
∴,
即,解得,
此时点P与点B重合,点D和A重合,
综合上述:当或或时,是等腰三角形,
即的大小是或或.
【点睛】此题考查了等腰三角形的性质,熟记等腰三角形有两个底角相等并应用是解题的关键.
答案第1页,共2页
答案第1页,共2页
考试分数:120分 考试时间:100分钟
一、单选题(本大题共10小题,共30分)
1.如图,屋顶钢架外框是等腰三角形,其中,工人师傅在焊接立柱时,只用找到的中点D,这就可以说明竖梁垂直于横梁了,工人师傅这种操作方法的依据是( )
A.等边对等角 B.等角对等 C.垂线段最短 D.等腰三角形“三线合一”
第1题图 第2题图 第3题图
2.如图,在直角三角形中,,作图痕迹如图所示,若,,则的面积是( )
A.1 B. C.2 D.
3.如图,点在线段上,点在线段上,且和均是等边三角形,那么( )
A. B. C. D.
4.校园湖边一角的形状如图所示,其中,,表示围墙,若在线段右侧的区域中找到一点P修建一个观赏亭,使点P到三面墙的距离都相等,则点P在( )
A.线段、的交点 B.、角平分线的交点
C.线段、垂直平分线的交点 D.线段、垂直平分线的交点
5.如图,在中,,要求在上找一点,使将分成两个等腰三角形. 现有如下两种设计方案,下列说法正确的是( )
方案一:作的平分线,使其交于点;
方案二:作的垂直平分线,使其交于点
A.两种方案都正确 B.只有方案一正确
C.只有方案二正确 D.两种方案都不正确
第5题图 第6题图 第7题图
6.如图所示,点O在点A的正北方,相距千米,,.则点B相对于点A的位置可以表示为( )
A.点B在点A的南偏东,距离20千米
B.点B在点A的南偏东,距离40千米
C.点B在点A的北偏西,距离40千米
D.点B在点A的北偏西,距离20千米
7.“八一薪火相传,七秩桃李芬芳”,今年是我校建校七十周年,为传承学校优良传统和红色基因,展示自建校以来各历史时期的文档资料和实物,学校将校本部的“大白楼”布置为校史馆。如图1所示为“大白楼”的正门,它的顶部可以看作如图2所示的等腰三角形,已知米,米,则的面积为( )平方米.
A.40 B.24 C.20 D.12
8.只用圆规来验证纸片的两边是否平行的探究活动中,小明的方法是:在纸片的一边上取线段,用圆规在另一边上截取,使,如图1.用圆规比较和的长度,若相同则平行.小刚的方法是:折叠纸条,使和重合,交于点F,折痕为和,如图2.用圆规比较,,的长度,若,则平行.则正确的是( )
A.小明的方法正确,小刚的方法错误
B.小明和小刚的方法都正确
C.小明的方法错误,小刚的方法正确
D.小明和小刚的方法都错误
第8题图 第9题图
9.如图,是某生产线的横截面示意图,MN表示长度为20米的笔直传送带,在MN的中点正上方3米处,有一个专用消毒喷头,(喷头大小、长度均忽略不计),喷头位置用点p表示,此时MN上有一个边长为2米的正方形盒子ABCD,则在盒子随传送带从点M移动到点N的过程中,以C、D、P三点为顶点的三角形是等腰三角形的时刻共有( )
A.5个 B.4个 C.3个 D.2个
10.老师在黑板上出了这样的一道练习题:如图,中,,是的角平分线,过点D作交于点E,交的平行线于点F,求证:.
嘉琪的解答如下:
证明:∵中,,是角平分线(已知), ∴, ∵(已知), ∴(两直线平行,内错角相等) 又∵(对顶角相等), ∴(▲), ∴(全等三角形对应边相等). ∴(等量代换).
下列选项错误的是( )
A.★表示 B.直接依据●表示等腰三角形“三线合一”
C.※表示 D.直接依据▲表示
二、填空题(本大题共5小题,共15分)
11.如图1,小明用尺规作出∠AOB的角平分线OC.为探索作图的道理,在图1中连接CE,CD得到图2,根据作法可得COE≌COD.他判定两个三角形全等的依据是
12.如图1,是某超市自动扶梯,如图2,是其的示意图,大厅两层之间的距离米,自动扶梯的倾角为30°,若自动扶梯运行速度米/秒,则顾客乘自动扶梯上一层楼的时间为 秒.
13.数学活动课上,志强用硬纸板剪了一个等腰三角形,但因失误同时剪掉该三角形的一个角,如图所示,经测量,,则被剪掉的的度数为 .
第13题图 第14题图 第15题图
14.如图,在中,,,.在上取一点,上取一点,连接,若,过点作,且点在的右侧,则的度数为 .
15.如图,是边长为2的等边三角形,直线经过顶点,且与边平行,在直线上有一点,当的值为 时,使得.
三、解答题(本大题共8小题,共75分)
16.如图,在等边三角形中,是中线,延长至,使,求证:.
17.如图,,垂足为D,且,.点E从B点沿射线向右以2个单位/秒的速度匀速运动,F为的中点,连接,设点E运动的时间为t.
(1)当t为何值时,;
(2)当时,判断的形状,并说明理由.
18.如图,,交于点F,点C在线段上,且,,,连接,.
(1)求证:;
(2)若,,求的度数.
19.如图,在中,,是过点A的直线,于D,于点E;
(1)若B、C在的同侧(如图1所示)且.求证:;
(2)若B、C在的两侧(如图2所示),且,其他条件不变,与仍垂直吗?若是请给出证明;若不是,请说明理由.
20.有一块等腰三角形木板,其中(如图),王师傅准备把它分成全等的两部分, 小明和小刚分别设计了两种方案:
(1)小明:确定BC的中点D,连结(如图1).
(2)小刚:作于D(如图2).
王师傅说两种办法都行,请选择一种说出其中的道理(写出已知、求证、证明).
21.某天,暴雨突然来袭,两艘搜救艇接到消息,在海面上有遇险船只从A、B两地发出求救信号.于是,第一艘搜救艇以20海里/时的速度离开港口O沿北偏东40°的方向向A地出发,同时,第二艘搜救艇也从港口O出发,以15海里/时的速度向B地出发,2小时后,他们同时到达各自的目标位置.此时,他们相距50海里.
(1)求第二艘搜救艇的航行方向是北偏西多少度?(求的大小)
(2)由于B地需要被援救的人数较多,故需要搭载人数较少的第一艘搜救艇改道去到B地支援,在从A地前往到B地的过程中,与港口O最近的距离是多少?
22.已知,是一条角平分线.
【探究发现】如图1,若是的角平分线.可得到结论:.
小红的解法如下:
过点D作于点E,于点F,过点A作于点G,
∵是的角平分线,且,
∴______.
∴______,
又∵,
∴______.
【类比探究】如图2,若是的外角平分线,与的延长线交于点D.
求证:
【拓展应用】如图3,在中,,分别是的角平分线且相交于点D,,直接写出的值是______.
23.综合与探究:
在综合实践课上,张老师首先出示了例题.
例题:在等腰三角形中.,求的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏同学编了如下一题:
变式:在等腰三角形中,,求的度数
(1)请你解答以上变式题;
(2)解(1)后,小敏发现,的度数不同,得到的度数的个数也可能不同,在等腰三角形中,设,当 有三个不同的度数时,请你探索的取值范围然后张老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动如图,在 中,,,将一块足够大的直角三角尺按如图所示位置放置,顶点在线段上滑动(点不与,重合),三角尺的直角边始终经过点 ,并且与 的夹角 ,斜边交于点
(3)小华发现在点的滑动过程中,的形状也在改变,请你探索可以是等腰三角形吗?若不可以,请说明理由;若可以,请求出的大小
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据等腰三角形的性质解答即可.
【详解】解:∵,,
∴,
故工人师傅这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
【点睛】本题考查等腰三角形的性质,熟知等腰三角形“三线合一”性质是解答的关键.
2.C
【分析】本题考查了角平分线的性质,过点作于点,根据作图可得是的角平分线,则,进而根据三角形的面积公式,即可求解.
【详解】解:如图所示,过点作于点,
根据作图可得是的角平分线,
又直角三角形中,,
∴
∴的面积是,
故选:C.
3.D
【分析】本题考查了等边三角形的性质、三角形内角和定理、平角的定义;由等边三角形的性质和平角的定义以及三角形内角和定理即可得出结果.
【详解】解:∵和均是等边三角形,
∴,
∵,,,
∴,
∵,
∴;
故选:D.
4.B
【分析】由角平分线的性质定理:角平分线上的点到角两边的距离相等,可判断为D.
【详解】解:如图,、角平分线的交点P,,,,垂足分别为K,L,M,则,即点P到三面墙的距离相等;
故选:B
【点睛】本题考查角平分线的性质定理;掌握角平分线的性质定理是解题的关键.
5.A
【分析】本题主要考查等腰三角形的性质与判定和垂直平分线的性质,对于两种方案均证明,可得结论.
【详解】解:方案一:如图1中,
∵
∴,
∵平分,
∴,
∴,
∴为等腰三角形,
∴,
∴为等腰三角形;
方案二:如图2,
∵
∴,
∵是边的垂直平分线,
∴
∴,
∴为等腰三角形,
∴,
∴为等腰三角形;
故选项A正确,
故选:A.
6.C
【分析】连接,得到等边,根据方位角的定义判断即可.
【详解】如图,连接,
∵,,
∴是等边三角形,
∴,
∴点B在点A的北偏西,距离40千米,
故选C.
【点睛】本题考查了等边三角形的判定和性质,方位角的应用,熟练掌握等边三角形的判定,方位角的意义是解题的关键.
7.D
【分析】过点A作,根据等腰三角形的定义可得为三角形的高,即可求得结果.
【详解】解:过点A作,如图所示:
∵米,
∴垂直平分,
∵米,
∴米,
根据勾股定理可得:米,
∴(平方米),
故答案选:D.
【点睛】本题考查了等腰三角形的性质,根据勾股定理求出高的长是解题的关键.
8.B
【分析】在图1中,连接,可证明,得,所以,可知小明的方法正确;在图2中,由,得,由折叠得,则,所以,可知小刚的方法正确,于是得到问题的答案.
【详解】解:如图1,连接,
在和中,,
∴,
∴,
∴,
∴小明的方法正确;
如图2,∵,
∴,
由折叠得,
∴,
∴,
∴小刚的方法正确,
故选:B.
【点睛】此题重点考查平行线的判定与性质、全等三角形的判定与性质、等腰三角形的性质等知识,证明两条直线被第三条直线所截得的内错角相等是解题的关键.
9.A
【分析】根据已知条件,利用等腰三角形的性质分情况讨论即可.
【详解】解:∵四边形为正方形
∴,
∵,在中点,
∴,
∴①当正方形在上,时,为等腰三角形;
②当正方形在 上,时,为等腰三角形;
③当过正方形边中点上时,,为等腰三角形;
④当正方形在上,时,为等腰三角形;
⑤当正方形在上,时,为等腰三角形;
综上所述,以、、三点为顶点的三角形是等腰三角形的时刻共有5个.
故选:.
【点睛】本题考查了等腰三角形的性质,正确理解题意、熟练掌握等腰三角形的性质是解题的关键.
10.D
【分析】根据等腰三角形的性质及全等三角形的性质与判定可进行求解.
【详解】证明:∵中,,是角平分线(已知),
∴(等腰三角形的“三线合一”),故A,B选项正确,不符合题意;
∵(已知),
∴(两直线平行,内错角相等)故C选项正确,不符合题意;
又∵(对顶角相等),
∴(),故D选项错误,符合题意;
∴(全等三角形对应边相等).
∴(等量代换);
故选D.
【点睛】本题主要考查等腰三角形的性质及全等三角形的性质与判定,熟练掌握等腰三角形的性质及全等三角形的性质与判定是解题的关键.
11.SSS
【分析】根据SSS证明三角形全等即可.
【详解】解:由作法可知:OE=OD,EC=DC,
在COE和COD中,
,
∴COE≌COD(SSS),
∴∠COE=∠COD,
∴OC平分∠AOB.
故答案为:SSS.
【点睛】本题考查作图-复杂作图,全等三角形的判定等知识,解题的关键是读懂图形中的信息,属于基础题型.
12.26
【分析】此题利用查直角三角形的性质求得自动扶梯的长,则顾客乘自动扶梯上一层楼的时间可求.
【详解】解:∵30°锐角所对直角边等于斜边的一半,
∴顾客乘自动扶梯上一层楼的距离为2h=13米,
∴顾客乘自动扶梯上一层楼的时间为13÷0.5=26秒.
【点睛】解决此类题目的关键是要熟记30°锐角所对直角边等于斜边的一半.注意数学在实际生活中的运用.
13.或或
【分析】分、、为顶角讨论即可求解.
【详解】解:当为顶角时,和为底角,
∵,
∴;
当为顶角时,和为底角,
∵,
∴;
当为顶角时,和为底角,
∵,
∴,
∴;
∴被剪掉的的度数为或或.
故答案为:或或.
【点睛】本题考查了等腰三角形的性质,三角形内角和定理等知识,明确题意,合理分类讨论,找出所求问题需要的条件是解题的关键.
14.
【分析】在中,由三边的长度可得出,进而可得出为直角三角形且,由于平行线之间有拐点,所以过点C作交AB于点M,则,利用平行的性质可得出的度数,结合可求出的度数,再利用“两直线平行,内错角相等”即可求出的度数.
【详解】解:在中,,,,
∵,即,
∴为直角三角形且.
过点C作交AB于点M,则,如下图所示,
∵,,
∴,
∴.
又∵,
∴.
故答案为:.
【点睛】本题考查了勾股定理的逆定理以及平行线的性质,利用勾股定理的逆定理,找出并知道过拐点作已知直线的平行线是解题的关键.
15.2或4/4或2
【分析】在直线上分别截取,连接,根据等边三角形的性质即可解决问题.
【详解】解:当或4时,使得,理由如下:
∵是边长为2的等边三角形,
∴,
如下图,在直线上分别截取,点为中点,连接,
∴,
∵直线经过顶点,且与边平行,
∴,
∴,
∴,
∴;
如图,连接,
∵,
∵,
∴是等边三角形,
∴,,
∴,
∴.
∴当AP的值为2或4时,使得.
故答案为:2或4.
【点睛】本题主要考查了作图—尺规作图、平行线的性质、等边三角形的判定与性质、等腰三角形的性质等知识,解题关键是灵活运用所学知识.
16.见解析
【分析】本题考查了等边三角形的性质,三角形外角的性质,等腰三角形的判定和性质;
根据等边三角形的性质求出,,然后根据三角形外角的性质和等边对等角求出,得到,再根据等角对等边得出结论.
【详解】证明:∵在等边三角形中,是中线,
∴,,
∵,
∴,
∴,
∴.
17.(1)当时,;
(2)是直角三角形,理由见解析
【分析】(1)根据题意可得:,再根据线段中点的定义可得,从而可得,,由等腰三角形的性质得,则建立方程即可解答;
(2)当时,,,然后分别在和中,利用勾股定理求出和,最后利用勾股定理的逆定理证明是直角三角形,即可解答.
【详解】(1)解:由题意得:,
∵F为的中点,
∴,
∵,,
∴,,
∵,,
∴,
即,
解得:,
∴当时,;
(2)解:是直角三角形,
理由:当时,,
∴,
在中,,
在中,,
∵,,
∴,
∴是直角三角形.
【点睛】本题考查了勾股定理,勾股定理的逆定理,等腰三角形的性质,熟练掌握勾股定理,以及勾股定理的逆定理是解题的关键.
18.(1)见解析
(2)
【分析】本题考查了全等三角形的判定和性质,平行线的性质,等腰三角形的性质,三角形外角性质.
(1)根据,可得,即可得证,从而得出结论;
(2)根据全等三角形的性质,可得,,根据三角形外角的性质,可得,根据等腰三角形的性质即可求出的度数.
【详解】(1)证明:,
,
在和中,
,
,
;
(2)解:,
,,
,
,
,
,
,
.
19.(1)见解析
(2),见解析
【分析】本题主要考查了三角形全等的判定和性质.
(1)通过证明,根据全等三角形对应角相等,即可求证;
(2)用和(1)相同的方法证明,根据全等三角形对应角相等,即可求证.
【详解】(1)证明:∵,,
∴,
在和中,
∵,
∴.
∴
∵,
∴.
∴.
∴.
(2)解:.理由如下:
∵,,
∴,
在和中,
∵,
∴.
∴,
∵,
∴,即,
∴.
20.选择(1),证明见解析,或选择(2),证明见解析
【分析】选择(1),通过证明即可.或选择(2),通过证明即可.
【详解】选择(1),
已知:△ABC中,,,
求证:,
证明:在和中,
∴
选择(2),
已知:△ABC中,,,
求证:,
证明:∵,
∴,
在和中,
∴
【点睛】本题考查了全等三角形的判定,解决本题的关键是熟练掌握全等三角形的判定.
21.(1)50度
(2)24海里
【分析】(1)根据题意求出OA、OB,根据勾股定理的逆定理推证出即得;
(2)根据垂线段定理即得.
【详解】(1)由题得:海里/时×2小时海里;海里/时×2小时海里,
∵,,
∴,
∴为直角三角形,
∴,
∵由题知,
∴,
即第二艘搜救艇的航行方向是北偏西50度.
(2)过点O作,此时OE的长度即为最近距离,
由(1)知,,,
∴在中,有,
即,
∴,
答:与港口O最近的距离是24海里.
【点睛】本题考查了勾股定理和其逆定理的应用,能熟练运用勾股定理及和其逆定理是解决本题的关键.
22.(1);;;(2)见解析;(3)
【分析】探究发现:根据题干中的解题思路求解即可;
类比探究:过点D作于N,过点D作于M.过点A作于点P.利用角平分线的性质及等面积法证明即可;
拓展应用:在BC上取点G,使得,连接,先利用全等三角形的判定得出再由其性质及前面的结论求解即可.
【详解】探究发现:解:过点D作于点E,于点F,过点A作于点G,
∵是的角平分线,且,
∴
∴,
又∵,
∴,
故答案为:,;;
类比探究:证明:过点D作于N,过点D作于.过点A作于点P.
∵平分,
∴.
∴,
∴
拓展应用:在BC上取点G,使得,连接,
∵分别是的角平分线且相交于点D,
∴,,
∵,
∴,
∴,
∴
∴是的角平分线
由(1)知,,
设,,则,
由(1)知,
.
【点睛】题目主要考查角平分线的性质及全等三角形的判定和性质,三角形等面积法等,理解题意,熟练掌握运算角平分线的性质是解题关键.
23.(1)或或;(2)当且时,有三个不同的度数;(3)是或或
【分析】(1)分三种情况:当为顶角时,当为顶角时,当为顶角时,利用等腰三角形两底角相等解答;
(2)分为两种情况:①当时,②当时,根据等腰三角形的性质求解;
(3)分三种情况,利用等腰三角形的性质,分别探究是等腰三角形的情况.
【详解】解:(1)∵,
当为顶角时,为底角,则;
当为顶角时,为底角,;
当为顶角时,为底角,;
(2)分为两种情况:
①当时,只能为顶角,
∴的度数只有一个;
②当时,
若为顶角,则;
若为底角,为顶角,则;
若为底角,为底角,则;
当且且,即时,有三个不同的度数,
综上所述,可知当且时,有三个不同的度数;
(3)的形状可以是等腰三角形,,
①当时,是等腰三角形,
∴ ,
即,解得;
②当时,是等腰三角形,
∴,
即,解得;
③当时,是等腰三角形,
∴,
即,解得,
此时点P与点B重合,点D和A重合,
综合上述:当或或时,是等腰三角形,
即的大小是或或.
【点睛】此题考查了等腰三角形的性质,熟记等腰三角形有两个底角相等并应用是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
