第5章 相交线与平行线 单元同步检测试题 (含答案)
文档属性
| 名称 | 第5章 相交线与平行线 单元同步检测试题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 553.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 16:35:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章《相交线与平行线》单元检测题(可直接打印)
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.如图,不是平移设计的是 ( )
A. B. C. D.
2.如图,点A表示某个村庄,BC表示一条公路,现要开一条路直接由A村到公路BC,并使得费用最低,这样做的依据是 ( )
A.两点之间,线段最短 B.垂线段最短
C.过一点有且只有一条直线和已知直线垂直 D.两点确定一条直线
2题图 3题图 4题图
3.如图,两条直线相交于一点,如果,则的度数是 ( )
A. B. C. D.
4.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成
( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
5.已知P是直线AB外一点,过点P作直线AB的平行线,这样的平行线
A.有无数条 B.有且只有一条 C.不存在 D.不存在或只有一条
6.如图, 是两条直线 被直线 所截后形成的八个角,则能够判定直线 的是 ( )
A. B.
C. D.
7.P为直线m外一点,A,B,C为直线m上三点,PA=4cm, PB=5cm, PC=6cm,则点P到直线m的距离 ( )
A.等于 B.等于 C.小于 D.不大于
8.如图所示,利用工具测量角,则的度数为 ( )
A. B. C. D.
8题图 9题图 10题图
9. 如图,直角三角形AOB和直角三角形COD,∠AOB=∠COD=90°,∠B=30°,∠C=50°,点D在OA上,将图中的三角形COD绕点O按每秒5°的速度沿顺时针方向旋转一周,在旋转的过程中,在第多少秒时,边CD恰好与边AB平行 ( )
A.14 B.52 C.16或52 D.14或50
10. 如图,点D在直线AE上,量得∠CDE=∠A=∠C,有以下结论:①AB∥DC;②AD∥BC;③∠C=∠ADF;④∠A+∠EDF=180°,则上述结论正确的是 ( )
A.①②③④ B.①②③ C.①② D.①②④
二、填空题(每题3分,共24分)
11. 命题“同位角相等,两直线平行”的条件是 ,结论是 .
12.如图,于点,于点.若,,不考虑点与点重合的情况,则线段的长度的取值范围是 .
12题图 13题图
13.如图,直线相交于点,,平分.若则 .(用含的代数式表示)
14.如图,直线与,相交,,,要使直线与平行,直线 顺时针旋转的最小度数是 .
14题图 16题图 17题图
15.已知直线相交于点O,平分,且,射线,则 .
16.如图,直线、相交于点,.若与的度数之比为,则的度数是 .
17.如图,∠AOB的一边OA为平面镜,∠AOB=42°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,此时∠ODE=∠ADC,且反射光线DC恰好与OB平行,则∠DEB的度数是 .
18.如图:①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
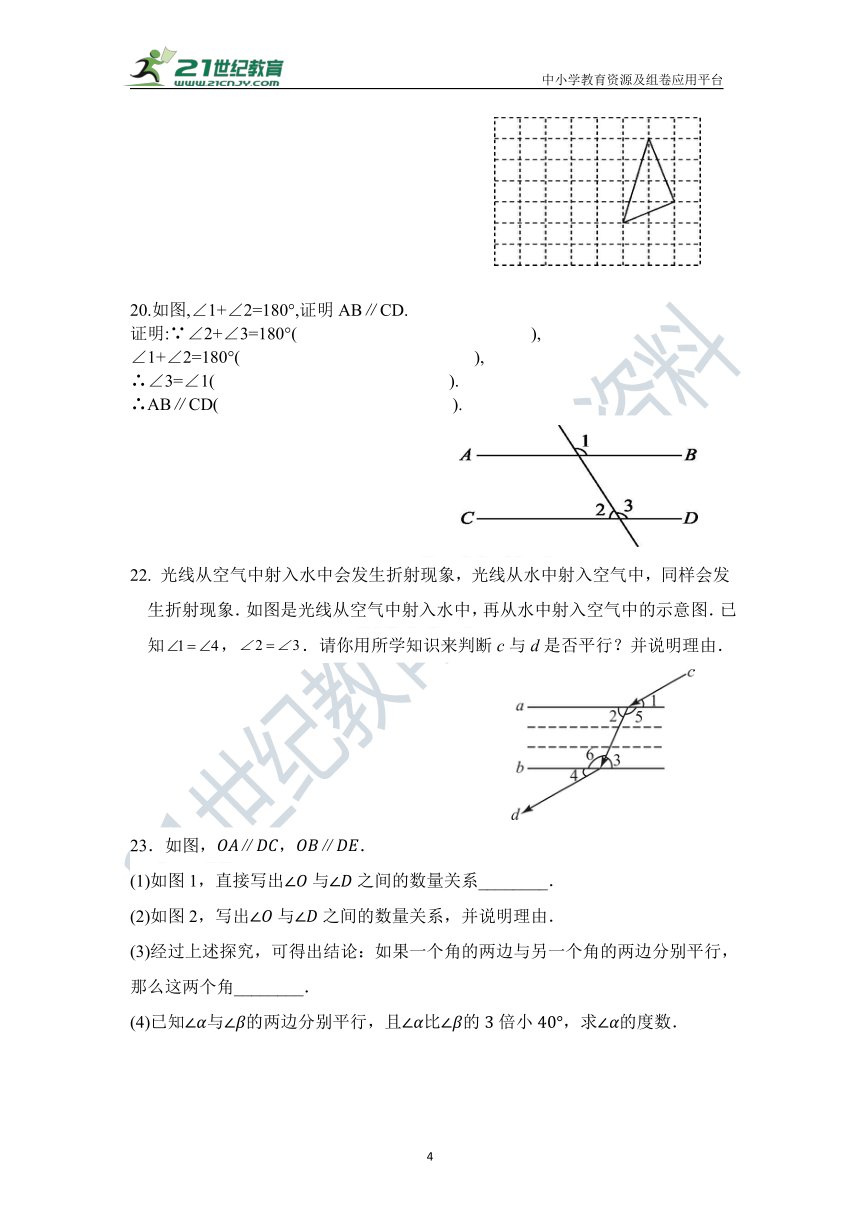
19.(1)画图:先把三角形向左平移3个单位长度,再向下平移1个单位长度;
(2)写出平移后三角形的面积是_______.
20.如图,∠1+∠2=180°,证明AB∥CD.
证明:∵∠2+∠3=180°( ),
∠1+∠2=180°( ),
∴∠3=∠1( ).
∴AB∥CD( ).
22. 光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
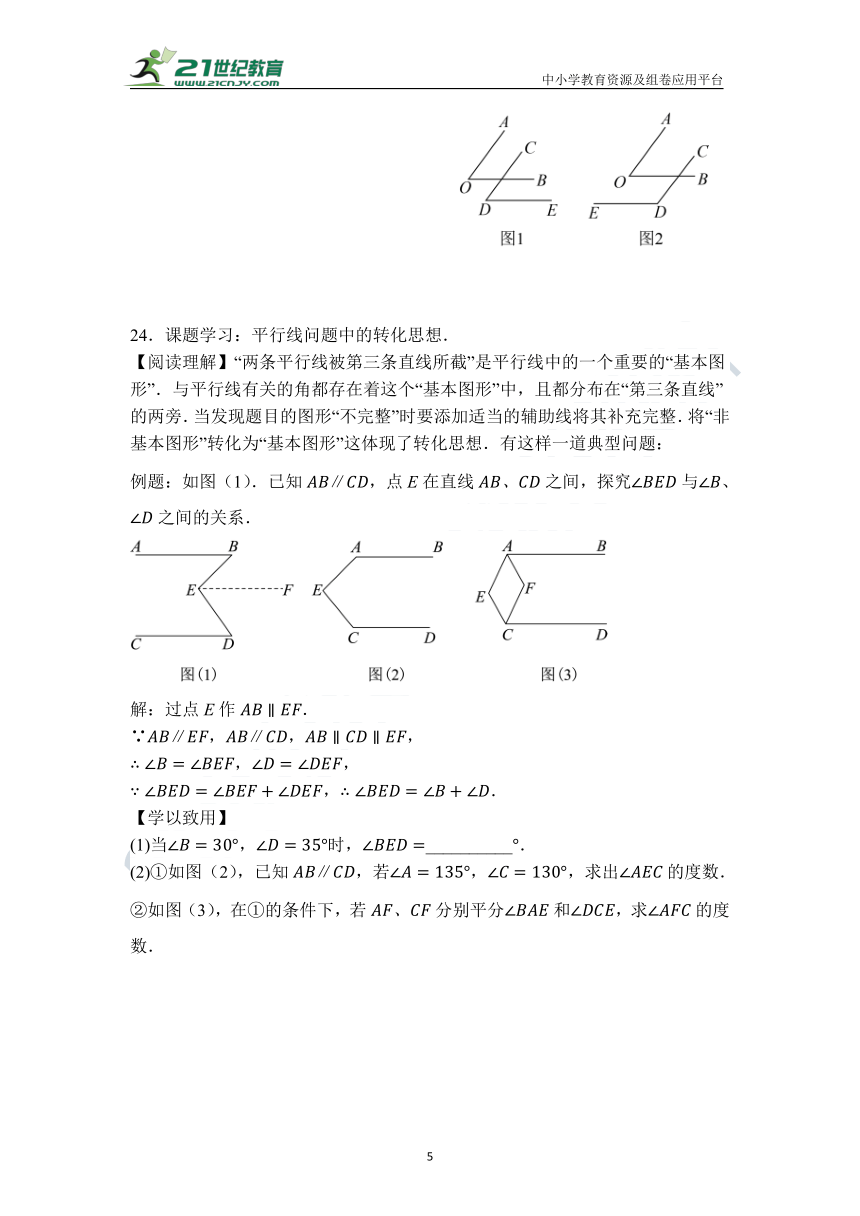
23.如图,,.
(1)如图1,直接写出与之间的数量关系________.
(2)如图2,写出与之间的数量关系,并说明理由.
(3)经过上述探究,可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________.
(4)已知与的两边分别平行,且比的倍小,求的度数.
24.课题学行线问题中的转化思想.
【阅读理解】“两条平行线被第三条直线所截”是平行线中的一个重要的“基本图形”.与平行线有关的角都存在着这个“基本图形”中,且都分布在“第三条直线”的两旁.当发现题目的图形“不完整”时要添加适当的辅助线将其补充完整.将“非基本图形”转化为“基本图形”这体现了转化思想.有这样一道典型问题:
例题:如图(1).已知,点E在直线之间,探究与、之间的关系.
解:过点E作.
∵,,,
,,
,.
【学以致用】
(1)当,时,__________.
(2)①如图(2),已知,若,,求出的度数.
②如图(3),在①的条件下,若分别平分和,求的度数.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A B B D A C A
二、填空题:
11. 两条直线被第三条直线所截,截得的同位角相等;这两条直线互相平行
12.
13.
14.
15.或
16.120
17.解:过点D作DF⊥AO交OB于点F.
∵入射角等于反射角,
∴∠1=∠3,
∵CD∥OB,
∴∠1=∠2(两直线平行,内错角相等);
∴∠2=∠3(等量代换);
在Rt△DOF中,∠ODF=90°,∠AOB=42°,
∴∠2=90°﹣42°=48°;
∴在△DEF中,∠DEB=180°﹣2∠2=84°.
故答案为:84°.
18.解:2条直线相交,最多有1个交点,
3条直线相交,最多有3个交点,即1+2=3,
4条直线相交,最多有6个交点,即1+2+3=6,
5条直线相交,最多有10个交点,即1+2+3+4=10,
……
10条直线相交,最多有45个交点,即1+2+3+4+…+7+8+9=45,
故答案为:45.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.(1)
(2)3.5
20.
21. 解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
23.(1)解:如图,设与交于点.
,
,
,
,
,
故答案为: ;
(2)解:,
理由:如图:
,
,
,
,
;
故答案为:;
(3)综上所述,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;
故答案为:相等或互补;
(4)解:由题意,得,
分两种情况讨论:
①当时,,
解得,
,
②当时,,
解得,
,
综上所述,的度数是或.
24.(1)解:∵,,,
∴;
故答案为:65;
(2)①解:如图所示过点E作,
因为,,
所以,
所以,,
又因为,,
所以,,
所以.
②因为,平分,
所以,
同理:.
由(1)可知:.
1
第五章《相交线与平行线》单元检测题(可直接打印)
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.如图,不是平移设计的是 ( )
A. B. C. D.
2.如图,点A表示某个村庄,BC表示一条公路,现要开一条路直接由A村到公路BC,并使得费用最低,这样做的依据是 ( )
A.两点之间,线段最短 B.垂线段最短
C.过一点有且只有一条直线和已知直线垂直 D.两点确定一条直线
2题图 3题图 4题图
3.如图,两条直线相交于一点,如果,则的度数是 ( )
A. B. C. D.
4.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成
( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
5.已知P是直线AB外一点,过点P作直线AB的平行线,这样的平行线
A.有无数条 B.有且只有一条 C.不存在 D.不存在或只有一条
6.如图, 是两条直线 被直线 所截后形成的八个角,则能够判定直线 的是 ( )
A. B.
C. D.
7.P为直线m外一点,A,B,C为直线m上三点,PA=4cm, PB=5cm, PC=6cm,则点P到直线m的距离 ( )
A.等于 B.等于 C.小于 D.不大于
8.如图所示,利用工具测量角,则的度数为 ( )
A. B. C. D.
8题图 9题图 10题图
9. 如图,直角三角形AOB和直角三角形COD,∠AOB=∠COD=90°,∠B=30°,∠C=50°,点D在OA上,将图中的三角形COD绕点O按每秒5°的速度沿顺时针方向旋转一周,在旋转的过程中,在第多少秒时,边CD恰好与边AB平行 ( )
A.14 B.52 C.16或52 D.14或50
10. 如图,点D在直线AE上,量得∠CDE=∠A=∠C,有以下结论:①AB∥DC;②AD∥BC;③∠C=∠ADF;④∠A+∠EDF=180°,则上述结论正确的是 ( )
A.①②③④ B.①②③ C.①② D.①②④
二、填空题(每题3分,共24分)
11. 命题“同位角相等,两直线平行”的条件是 ,结论是 .
12.如图,于点,于点.若,,不考虑点与点重合的情况,则线段的长度的取值范围是 .
12题图 13题图
13.如图,直线相交于点,,平分.若则 .(用含的代数式表示)
14.如图,直线与,相交,,,要使直线与平行,直线 顺时针旋转的最小度数是 .
14题图 16题图 17题图
15.已知直线相交于点O,平分,且,射线,则 .
16.如图,直线、相交于点,.若与的度数之比为,则的度数是 .
17.如图,∠AOB的一边OA为平面镜,∠AOB=42°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,此时∠ODE=∠ADC,且反射光线DC恰好与OB平行,则∠DEB的度数是 .
18.如图:①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.(1)画图:先把三角形向左平移3个单位长度,再向下平移1个单位长度;
(2)写出平移后三角形的面积是_______.
20.如图,∠1+∠2=180°,证明AB∥CD.
证明:∵∠2+∠3=180°( ),
∠1+∠2=180°( ),
∴∠3=∠1( ).
∴AB∥CD( ).
22. 光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
23.如图,,.
(1)如图1,直接写出与之间的数量关系________.
(2)如图2,写出与之间的数量关系,并说明理由.
(3)经过上述探究,可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________.
(4)已知与的两边分别平行,且比的倍小,求的度数.
24.课题学行线问题中的转化思想.
【阅读理解】“两条平行线被第三条直线所截”是平行线中的一个重要的“基本图形”.与平行线有关的角都存在着这个“基本图形”中,且都分布在“第三条直线”的两旁.当发现题目的图形“不完整”时要添加适当的辅助线将其补充完整.将“非基本图形”转化为“基本图形”这体现了转化思想.有这样一道典型问题:
例题:如图(1).已知,点E在直线之间,探究与、之间的关系.
解:过点E作.
∵,,,
,,
,.
【学以致用】
(1)当,时,__________.
(2)①如图(2),已知,若,,求出的度数.
②如图(3),在①的条件下,若分别平分和,求的度数.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A B B D A C A
二、填空题:
11. 两条直线被第三条直线所截,截得的同位角相等;这两条直线互相平行
12.
13.
14.
15.或
16.120
17.解:过点D作DF⊥AO交OB于点F.
∵入射角等于反射角,
∴∠1=∠3,
∵CD∥OB,
∴∠1=∠2(两直线平行,内错角相等);
∴∠2=∠3(等量代换);
在Rt△DOF中,∠ODF=90°,∠AOB=42°,
∴∠2=90°﹣42°=48°;
∴在△DEF中,∠DEB=180°﹣2∠2=84°.
故答案为:84°.
18.解:2条直线相交,最多有1个交点,
3条直线相交,最多有3个交点,即1+2=3,
4条直线相交,最多有6个交点,即1+2+3=6,
5条直线相交,最多有10个交点,即1+2+3+4=10,
……
10条直线相交,最多有45个交点,即1+2+3+4+…+7+8+9=45,
故答案为:45.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.(1)
(2)3.5
20.
21. 解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
23.(1)解:如图,设与交于点.
,
,
,
,
,
故答案为: ;
(2)解:,
理由:如图:
,
,
,
,
;
故答案为:;
(3)综上所述,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;
故答案为:相等或互补;
(4)解:由题意,得,
分两种情况讨论:
①当时,,
解得,
,
②当时,,
解得,
,
综上所述,的度数是或.
24.(1)解:∵,,,
∴;
故答案为:65;
(2)①解:如图所示过点E作,
因为,,
所以,
所以,,
又因为,,
所以,,
所以.
②因为,平分,
所以,
同理:.
由(1)可知:.
1
