【素养进阶结构化评价工具】 人教版 五年级下册第三单元《长方体和正方体》作业设计
文档属性
| 名称 | 【素养进阶结构化评价工具】 人教版 五年级下册第三单元《长方体和正方体》作业设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 445.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
单元评价导语
第 三 单 元 长 方 体 和 正 方 体
同学们,这一单元我们走进了长方体和正方体的世界,探索了它们的形状、特性和应用。现在,我们要一起回顾和检验自己的学习成果啦!准备好接受挑战了吗?让我们展示学习成果,继续在数学的海洋里畅游吧!加油哦!
单元知识结构
单元评价目标
目标序号 内容要求 核心素养 认知类型
100301 长方体和正方体的特征 空间观念 理解
100302 正方体展开图与立体图形之 间的关系 空间观念 推理意识 理解
100303 长方体和正方体的表面积 空间观念几何直观 掌握
100304 体积的意义、容积的意义 量感 推理意识 了解
100305 体积单位和容积单位 量 感 推理意识 了解
100306 长方体和正方体的体积计算公式;不规则物体体积的计 算方法 空间观念 掌握
100307 体(容)积单位间的进率及 简单的换算 量感 推理意识 理解
100308 能自主整理单元知识结构, 形成认知结构 创新意识 分析
单元评价工具
第一课时 长方体和正方体的认识
★基础素养★
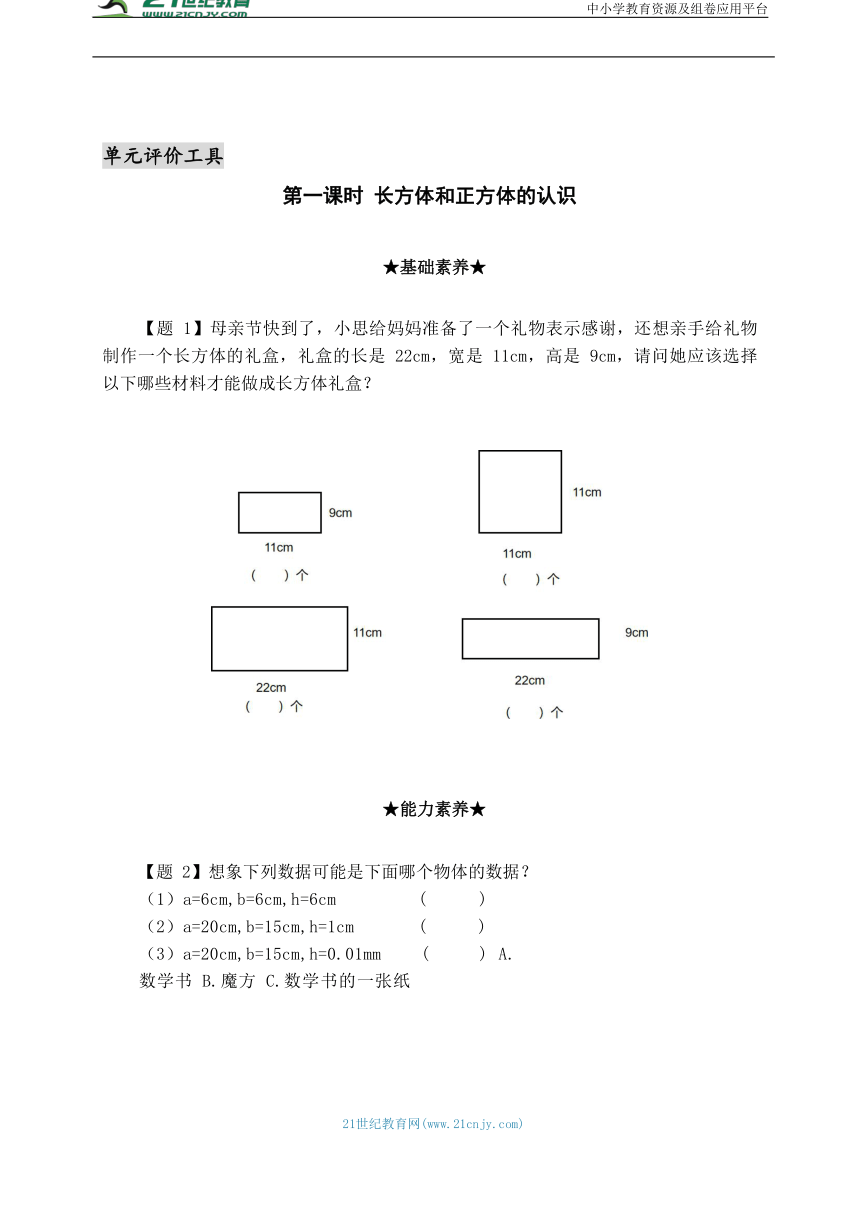
【题 1】母亲节快到了,小思给妈妈准备了一个礼物表示感谢,还想亲手给礼物制作一个长方体的礼盒,礼盒的长是 22cm,宽是 11cm,高是 9cm,请问她应该选择以下哪些材料才能做成长方体礼盒?
★能力素养★
【题 2】想象下列数据可能是下面哪个物体的数据?
(1)a=6cm,b=6cm,h=6cm ( )
(2)a=20cm,b=15cm,h=1cm ( )
(3)a=20cm,b=15cm,h=0.01mm ( ) A.数学书 B.魔方 C.数学书的一张纸
★综合素养★
【题 3】如下图。你能根据长、宽、高选一选长方体的上下面、前后面、左右面吗?
(1)上下面( ) 前后面( ) 左右面( )
(2)如果其中一条也缩短到 5 厘米 ,选一选这个长方体的上下面、前后面、左右面?
(3)上下面( ) 前后面( ) 左右面( ),如果现在的长方体的三条棱都变成 5 厘米,那么它变成了什么图形,它有什么特点?
第二课时 展开与折叠
★基础素养★
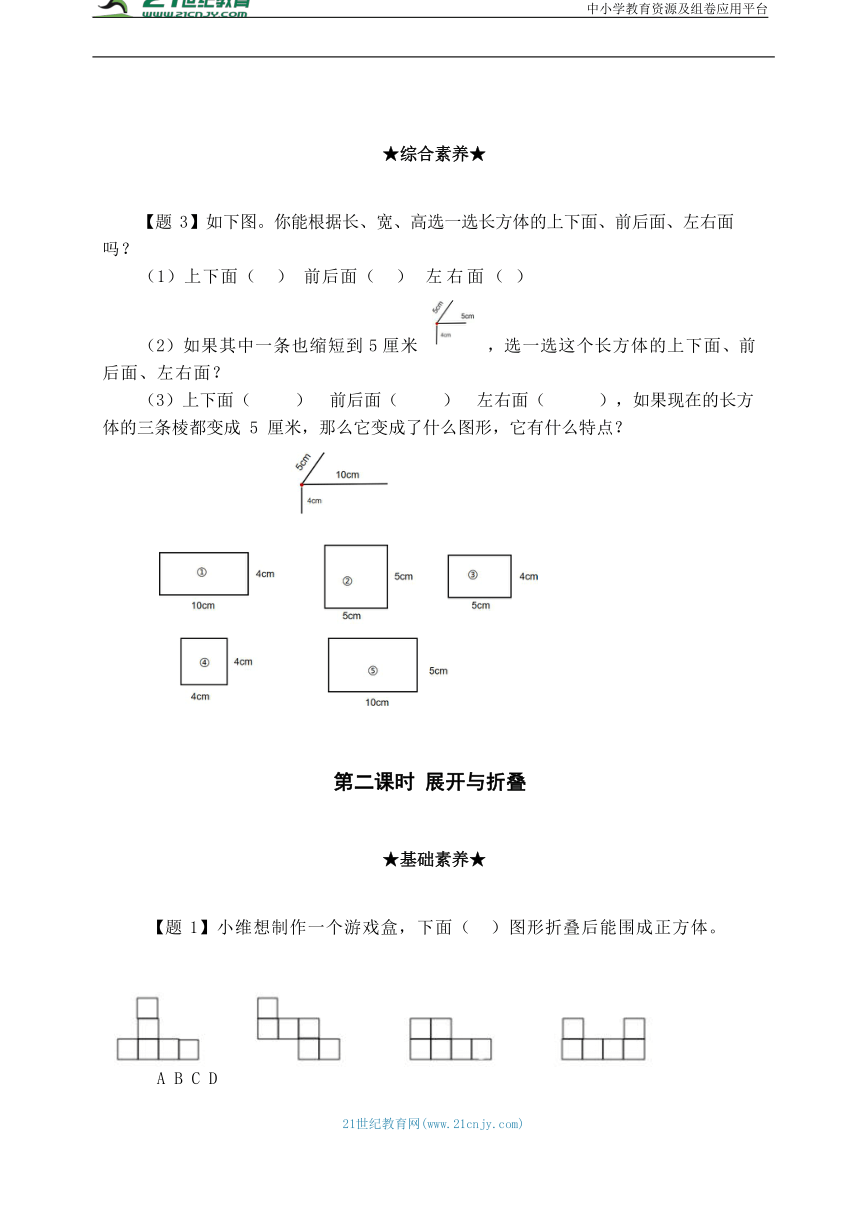
【题 1】小维想制作一个游戏盒,下面( )图形折叠后能围成正方体。
A B C D
★能力素养★
【题 2】将右面平面展开图折叠成正方体后,
相对面上的两个数之和都是 9,则 a+b=( )。
★综合素养★
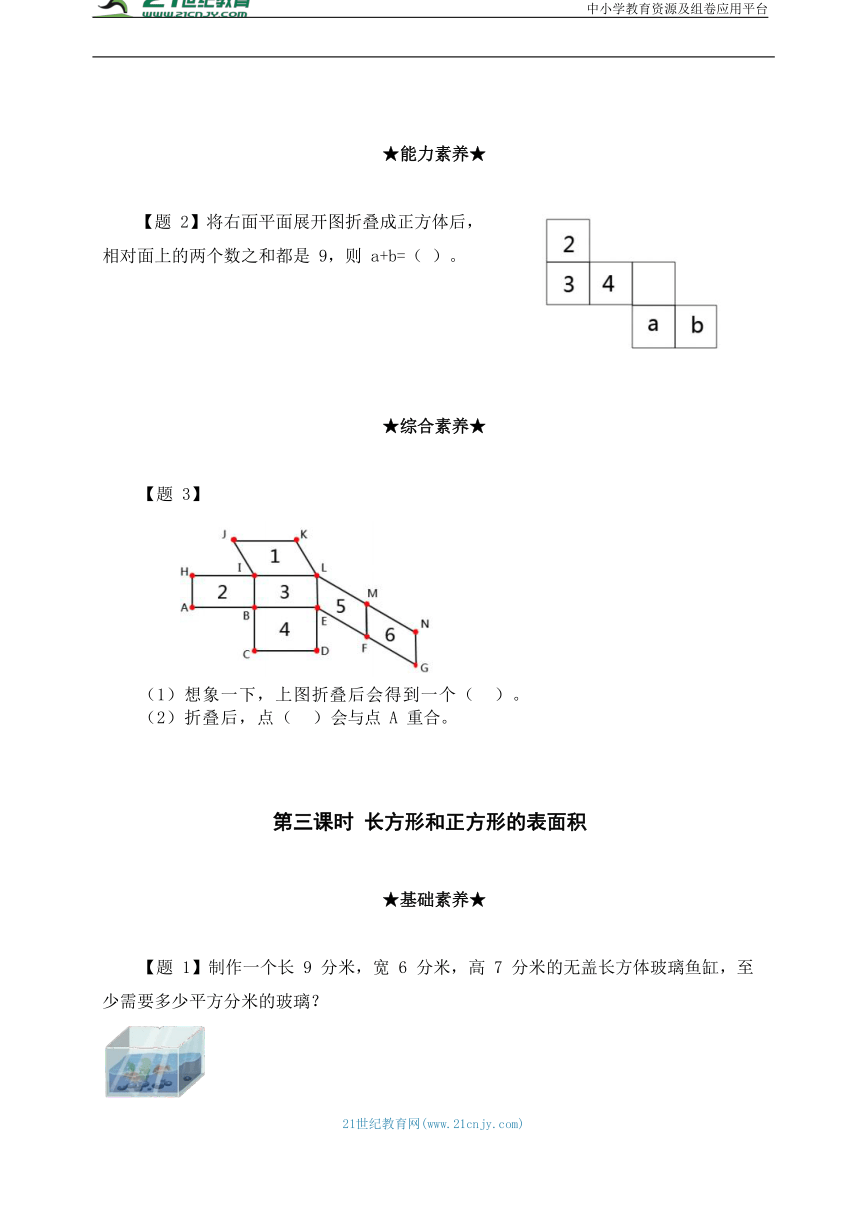
【题 3】
(1)想象一下,上图折叠后会得到一个( )。
(2)折叠后,点( )会与点 A 重合。
第三课时 长方形和正方形的表面积
★基础素养★
【题 1】制作一个长 9 分米,宽 6 分米,高 7 分米的无盖长方体玻璃鱼缸,至少需要多少平方分米的玻璃?
★能力素养★
【题 2】一个长方体的高削去 5cm,它就变成一个棱长为 3dm 的正方体,原来长方体的表面积是多少平方分米?
★综合素养★
【题 3】一盒牛奶长 8cm,宽 6cm,高 13cm。商场进行促销,把 3 盒装在一起销售。请你设计一下,怎样才能最节省包装纸?并算一算,至少需要多少平方厘米的包装纸。
画一画:我想到了( )种方案。(画示意图,标明数据)
算一算:第( )种方案最节省包装纸,需要包装纸的用量是:
第四课时 体积与容积
★基础素养★
【题 1】爸爸做了一个长方体的箱子,他估测了一下箱子能占多大的空间,就是求它的( );要求箱子能装多少东西是求它的( );准备购买油漆涂在箱子上就是求这个长方体的( ),并用金属条进行装饰是求金属条的( )。由于使用的材料很厚实,箱子的体积比箱子的容积要( )。
★能力素养★
【题 2】1.用 8 个相同的小正方体,按要求动手搭一搭并回答问题。
搭出两个不同的几何体,使它们的体积相同,搭出的几何体体积是多少个小正方体?
搭出两个几何体,使其中一个几何体的体积是另一个的 3 倍。搭出的几何体的体积分别是多少个小正方体?
用 8 个相同的小正方体去搭出不同的长方体,观察搭出的长方体的体积有变化吗 你们发现什么规律
★综合素养★
【题 3】小思买了两盒完全一样的月饼(如下图)。
小思想把这两盒月饼装进下面的大快递箱里邮寄出去,能否装得下?写出你判断的理由。(快递箱纸板的厚度忽略不计)
如果请你设计一个大快递箱,使它能正好装下两盒月饼(纸板的厚度忽略不计),那么它的长、宽、高分别是( )厘米、( )厘米、( )厘米,这样的大快递箱的容积正好等于( )的体积。
第五课时 体积单位与容积单位
★基础素养★
【题 1】在横线上填写合适的单位或数量。
一瓶眼药水约 30
纯净水桶大约能容纳 19 水
洗衣机体积大约是 700
运货集装箱的容积是 40
1 立方厘米的小正方体可以容纳 颗黄豆两个拳头的体积大约是 立方分米
★能力素养★
【题 2】用几个体积是 1 立方厘米的正方体木块摆成一个几何体,从上面看的图形如下图。
上 面 左 面
这几个几何体的体积最大是( )立方厘米,最小是( )立方厘米。
★综合应用★
【题 3】为了比较土豆和红薯的体积,小华做了如下实验。
(1)想一想,土豆体积和红薯体积那个大一些?( )(填入土豆/红薯)
(2)土豆体积是( ),红薯体积是( )。
第六课时 长方形和正方形的体积
★基础素养★
【题 1】小维在用 1cm 的小正方体玩积木拼搭,拼成了一个长方体,写出了下列算式,你看懂了吗?请你写一写。
小维先计算了 5×4=20,再算 20×3=60(cm )。
5×4 表 示 ( );20×3 表 示 ( ) 。
★能力素养★
【题 2】有一个长方体的木箱,它的长、宽、高分别是 30 厘米、20 厘米、15 厘
米。现在要在木箱里面装进一些小盒子,每个小盒子的长、宽、高分别是 10 厘米、
5 厘米、3 厘米,这个木箱子最多可以装多少个小盒子?
★综合素养★
【题 3】小思利用一块长方形铁皮(如图),制作一个盒子,铁皮长 40 厘米,宽
30 厘米,在这块铁皮的四周各减去一个边长是 10 厘米的小正方形,然后通过折叠、焊接,做成一个无盖的长方体水箱。
(
)
30cm
40cm
画一画:尝试将小思的裁剪步骤在上图中画一画,并标出裁剪后的相关数据。
这个长方体水箱的表面积是多少平方厘米?
往里面倒入 5 厘米高的水后,他将一个假山石放入水里,水面上升了 2 厘米,这个假山石的体积是多大?
第七课时 单位间的进率
★基础素养★
【题 1】
0.6dm =( )cm
想 :1dm =( )cm
500dm =( )m
想 :( )dm =1m
8L=( )mL
想 :1L=( )mL
★能力素养★
【题 2】某餐厅买了一种烤箱,内部尺寸为:600×300×400(单位 mm),这个烤箱的容积是多少升?
★综合应用★
【题 3】劳动课上,老师给每个小组准备了纸壳(如图),长 80CM,宽40CM。现在同学们要把纸壳折制成一个无盖的收纳盒(连接处和纸壳厚度忽略不计)。这个长方形的纸盒的容积是多少立方厘米?合多少?
单元作业
★知识地图★
(
)经过这一单元的学习,你已经掌握了关于长方体和正方体的许多知识点。现在, 假设你是一位小老师,需要向其他没有学过这个单元的同学介绍长方体和正方体的主要内容。你会如何将这些知识点进行整理和分类,以便清晰地展示它们之间的关系和层次?请尝试绘制一个知识图谱,将这一单元的重点知识和它们之间的联系呈现出来。
★知识运用★
“水杯之旅:从测量到包装的艺术”
【任务】“水杯创意之旅”活动正式开启!参与其中,你将亲手测量、设计并包装独一无二的水杯。发挥你的创意,探索生活中的美学奥秘,与伙伴们一同开启这段充满乐趣与惊喜的创意之旅!
第一步:水杯的测量与数据记录
从家里任意选出一个玻璃水杯,测量这个水杯的关键数据,为制作包装盒提供基础。用自己喜欢的方式记录测量的结果。
第二步:包装盒的设计
根据测量的数据,设计一个能够容纳水杯的包装盒。包装盒要确保水杯在盒内稳固不晃动。
请画出包装盒的示意图,并标出尺寸,并计算包装盒需要多大面积的材料。
第三步:包装盒的制作
选用合适的材料,动手制作包装盒。这个包装盒的容积是多少?
(包装盒图片粘贴处) 列式计算:
第四步:作品展示
分享在测量、设计和制作过程中的心得和体会。我的体会:
自我评价
评价维度 评价内容 评价等级
知识内容 我能准确测量水杯的尺寸,并能计算包装盒表面积和体积。 ☆ ☆ ☆
能力发展 我提升了自己的动手能力和解决问题的能力,形成了更为严谨和逻辑性的思维方式。 ☆ ☆ ☆
教育品质 我积极投入,勇于尝试,逐渐培养了对知识的好奇心和探究欲,同时也增强了自信心。 ☆ ☆ ☆
艺术审美 我感受到了艺术与科学的交融,提升了自己对美的感知能力和审美水平。 ☆ ☆ ☆
21世纪教育网(www.21cnjy.com)
单元评价导语
第 三 单 元 长 方 体 和 正 方 体
同学们,这一单元我们走进了长方体和正方体的世界,探索了它们的形状、特性和应用。现在,我们要一起回顾和检验自己的学习成果啦!准备好接受挑战了吗?让我们展示学习成果,继续在数学的海洋里畅游吧!加油哦!
单元知识结构
单元评价目标
目标序号 内容要求 核心素养 认知类型
100301 长方体和正方体的特征 空间观念 理解
100302 正方体展开图与立体图形之 间的关系 空间观念 推理意识 理解
100303 长方体和正方体的表面积 空间观念几何直观 掌握
100304 体积的意义、容积的意义 量感 推理意识 了解
100305 体积单位和容积单位 量 感 推理意识 了解
100306 长方体和正方体的体积计算公式;不规则物体体积的计 算方法 空间观念 掌握
100307 体(容)积单位间的进率及 简单的换算 量感 推理意识 理解
100308 能自主整理单元知识结构, 形成认知结构 创新意识 分析
单元评价工具
第一课时 长方体和正方体的认识
★基础素养★
【题 1】母亲节快到了,小思给妈妈准备了一个礼物表示感谢,还想亲手给礼物制作一个长方体的礼盒,礼盒的长是 22cm,宽是 11cm,高是 9cm,请问她应该选择以下哪些材料才能做成长方体礼盒?
★能力素养★
【题 2】想象下列数据可能是下面哪个物体的数据?
(1)a=6cm,b=6cm,h=6cm ( )
(2)a=20cm,b=15cm,h=1cm ( )
(3)a=20cm,b=15cm,h=0.01mm ( ) A.数学书 B.魔方 C.数学书的一张纸
★综合素养★
【题 3】如下图。你能根据长、宽、高选一选长方体的上下面、前后面、左右面吗?
(1)上下面( ) 前后面( ) 左右面( )
(2)如果其中一条也缩短到 5 厘米 ,选一选这个长方体的上下面、前后面、左右面?
(3)上下面( ) 前后面( ) 左右面( ),如果现在的长方体的三条棱都变成 5 厘米,那么它变成了什么图形,它有什么特点?
第二课时 展开与折叠
★基础素养★
【题 1】小维想制作一个游戏盒,下面( )图形折叠后能围成正方体。
A B C D
★能力素养★
【题 2】将右面平面展开图折叠成正方体后,
相对面上的两个数之和都是 9,则 a+b=( )。
★综合素养★
【题 3】
(1)想象一下,上图折叠后会得到一个( )。
(2)折叠后,点( )会与点 A 重合。
第三课时 长方形和正方形的表面积
★基础素养★
【题 1】制作一个长 9 分米,宽 6 分米,高 7 分米的无盖长方体玻璃鱼缸,至少需要多少平方分米的玻璃?
★能力素养★
【题 2】一个长方体的高削去 5cm,它就变成一个棱长为 3dm 的正方体,原来长方体的表面积是多少平方分米?
★综合素养★
【题 3】一盒牛奶长 8cm,宽 6cm,高 13cm。商场进行促销,把 3 盒装在一起销售。请你设计一下,怎样才能最节省包装纸?并算一算,至少需要多少平方厘米的包装纸。
画一画:我想到了( )种方案。(画示意图,标明数据)
算一算:第( )种方案最节省包装纸,需要包装纸的用量是:
第四课时 体积与容积
★基础素养★
【题 1】爸爸做了一个长方体的箱子,他估测了一下箱子能占多大的空间,就是求它的( );要求箱子能装多少东西是求它的( );准备购买油漆涂在箱子上就是求这个长方体的( ),并用金属条进行装饰是求金属条的( )。由于使用的材料很厚实,箱子的体积比箱子的容积要( )。
★能力素养★
【题 2】1.用 8 个相同的小正方体,按要求动手搭一搭并回答问题。
搭出两个不同的几何体,使它们的体积相同,搭出的几何体体积是多少个小正方体?
搭出两个几何体,使其中一个几何体的体积是另一个的 3 倍。搭出的几何体的体积分别是多少个小正方体?
用 8 个相同的小正方体去搭出不同的长方体,观察搭出的长方体的体积有变化吗 你们发现什么规律
★综合素养★
【题 3】小思买了两盒完全一样的月饼(如下图)。
小思想把这两盒月饼装进下面的大快递箱里邮寄出去,能否装得下?写出你判断的理由。(快递箱纸板的厚度忽略不计)
如果请你设计一个大快递箱,使它能正好装下两盒月饼(纸板的厚度忽略不计),那么它的长、宽、高分别是( )厘米、( )厘米、( )厘米,这样的大快递箱的容积正好等于( )的体积。
第五课时 体积单位与容积单位
★基础素养★
【题 1】在横线上填写合适的单位或数量。
一瓶眼药水约 30
纯净水桶大约能容纳 19 水
洗衣机体积大约是 700
运货集装箱的容积是 40
1 立方厘米的小正方体可以容纳 颗黄豆两个拳头的体积大约是 立方分米
★能力素养★
【题 2】用几个体积是 1 立方厘米的正方体木块摆成一个几何体,从上面看的图形如下图。
上 面 左 面
这几个几何体的体积最大是( )立方厘米,最小是( )立方厘米。
★综合应用★
【题 3】为了比较土豆和红薯的体积,小华做了如下实验。
(1)想一想,土豆体积和红薯体积那个大一些?( )(填入土豆/红薯)
(2)土豆体积是( ),红薯体积是( )。
第六课时 长方形和正方形的体积
★基础素养★
【题 1】小维在用 1cm 的小正方体玩积木拼搭,拼成了一个长方体,写出了下列算式,你看懂了吗?请你写一写。
小维先计算了 5×4=20,再算 20×3=60(cm )。
5×4 表 示 ( );20×3 表 示 ( ) 。
★能力素养★
【题 2】有一个长方体的木箱,它的长、宽、高分别是 30 厘米、20 厘米、15 厘
米。现在要在木箱里面装进一些小盒子,每个小盒子的长、宽、高分别是 10 厘米、
5 厘米、3 厘米,这个木箱子最多可以装多少个小盒子?
★综合素养★
【题 3】小思利用一块长方形铁皮(如图),制作一个盒子,铁皮长 40 厘米,宽
30 厘米,在这块铁皮的四周各减去一个边长是 10 厘米的小正方形,然后通过折叠、焊接,做成一个无盖的长方体水箱。
(
)
30cm
40cm
画一画:尝试将小思的裁剪步骤在上图中画一画,并标出裁剪后的相关数据。
这个长方体水箱的表面积是多少平方厘米?
往里面倒入 5 厘米高的水后,他将一个假山石放入水里,水面上升了 2 厘米,这个假山石的体积是多大?
第七课时 单位间的进率
★基础素养★
【题 1】
0.6dm =( )cm
想 :1dm =( )cm
500dm =( )m
想 :( )dm =1m
8L=( )mL
想 :1L=( )mL
★能力素养★
【题 2】某餐厅买了一种烤箱,内部尺寸为:600×300×400(单位 mm),这个烤箱的容积是多少升?
★综合应用★
【题 3】劳动课上,老师给每个小组准备了纸壳(如图),长 80CM,宽40CM。现在同学们要把纸壳折制成一个无盖的收纳盒(连接处和纸壳厚度忽略不计)。这个长方形的纸盒的容积是多少立方厘米?合多少?
单元作业
★知识地图★
(
)经过这一单元的学习,你已经掌握了关于长方体和正方体的许多知识点。现在, 假设你是一位小老师,需要向其他没有学过这个单元的同学介绍长方体和正方体的主要内容。你会如何将这些知识点进行整理和分类,以便清晰地展示它们之间的关系和层次?请尝试绘制一个知识图谱,将这一单元的重点知识和它们之间的联系呈现出来。
★知识运用★
“水杯之旅:从测量到包装的艺术”
【任务】“水杯创意之旅”活动正式开启!参与其中,你将亲手测量、设计并包装独一无二的水杯。发挥你的创意,探索生活中的美学奥秘,与伙伴们一同开启这段充满乐趣与惊喜的创意之旅!
第一步:水杯的测量与数据记录
从家里任意选出一个玻璃水杯,测量这个水杯的关键数据,为制作包装盒提供基础。用自己喜欢的方式记录测量的结果。
第二步:包装盒的设计
根据测量的数据,设计一个能够容纳水杯的包装盒。包装盒要确保水杯在盒内稳固不晃动。
请画出包装盒的示意图,并标出尺寸,并计算包装盒需要多大面积的材料。
第三步:包装盒的制作
选用合适的材料,动手制作包装盒。这个包装盒的容积是多少?
(包装盒图片粘贴处) 列式计算:
第四步:作品展示
分享在测量、设计和制作过程中的心得和体会。我的体会:
自我评价
评价维度 评价内容 评价等级
知识内容 我能准确测量水杯的尺寸,并能计算包装盒表面积和体积。 ☆ ☆ ☆
能力发展 我提升了自己的动手能力和解决问题的能力,形成了更为严谨和逻辑性的思维方式。 ☆ ☆ ☆
教育品质 我积极投入,勇于尝试,逐渐培养了对知识的好奇心和探究欲,同时也增强了自信心。 ☆ ☆ ☆
艺术审美 我感受到了艺术与科学的交融,提升了自己对美的感知能力和审美水平。 ☆ ☆ ☆
