北师大版五年级下册数学第二单元长方体(一)填空题训练(含答案)
文档属性
| 名称 | 北师大版五年级下册数学第二单元长方体(一)填空题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 511.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 14:00:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版五年级下册数学第二单元 长方体(一)填空题训练
1.站在固定的位置观察一个长方体,一次最多能看到( )个面。
2.一个长方体框架,长5厘米,宽4厘米,高3厘米,做这个框架共要( )厘米的铁丝;若在它的表面贴上塑料板,共要( )平方厘米塑料板。
3.一个长是8cm、宽是6cm、高是5cm的长方体灯笼,它的棱长总和是( )cm,六个面中最大的面的面积是( )cm2。
4.把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是( ) cm2。
5.观察一个长方体,一次最多看见它的( )个面,最少能看到( )个面。搭一个正方体,至少需要( )个小正方体。
6.用两个长5cm、宽4cm,高3cm的长方体拼成三种不同的长方体,最小的表面积是( )。
7.用一根长72分米的铁丝做一个长7分米,高5分米的长方体框架,它的宽是( )分米。
8.将几个棱长为5分米的正方体纸箱摆放在墙角处(如图),露在外面的面面积是( )分米2,在此基础上要把它堆成一个大正方体,至少还要( )个这样的正方体纸箱。
9.一个正方体的礼品盒,它的棱长是7dm,在所有的棱上粘上彩带,需要彩带( )dm。
10.3厘米、4厘米、5厘米长的小棒各有12根,用其中的小棒,可以搭成( )种不同形状的长方体(包括正方体)。
11.一个长方体的长、宽、高分别为10厘米、6厘米、6厘米,那么这个长方体最多有( )条棱长度相等,最多有( )个面形状相同,剩下的面都是( )形。
12.将3个棱长2分米的正方体拼成一个长方体,这个长方体的表面积比原来3个正方体的表面积之和( )(填“增加”或“减少”)( )平方分米。
13.一个正方体棱长6cm,表面积是( )cm2,棱长之和是( )cm。
14.一个游泳池长50m,宽25m,深2m,在池内四壁及池底贴上瓷砖,贴瓷砖的面积是( )平方米。
15.淘气在摆方块,如果按下图中的规律继续往下摆,第4组有( )个面露在外面。
16.如下图,正方体的展开图上有编号,请你写出相对面的号码:3的相对面是( ),4的相对面是( ),5的相对面是( )。
17.把两个棱长都是10cm的正方体拼成一个长方体后,表面积减少了( )cm2。
18.赵伯伯用一根长48dm的铁丝正好做一个正方体的框架,把它的各个面糊上彩纸,至少需要( )dm2的彩纸。
19.如下图,沿虚线可以折成一个( ),这个立体图形中有( )个长方形,它的表面积是( )平方厘米。(单位:厘米)
20.手工课上,淘气在一块长方体(高lcm)橡皮上挖出一个棱长1cm的正方体(如下图),表面积( )(填“增加”或“减少”)了( )dm2。
21.有5个棱长是4厘米的小正方体堆放在墙角处,有( )个面露在外面,露在外面的面积是( )平方厘米。
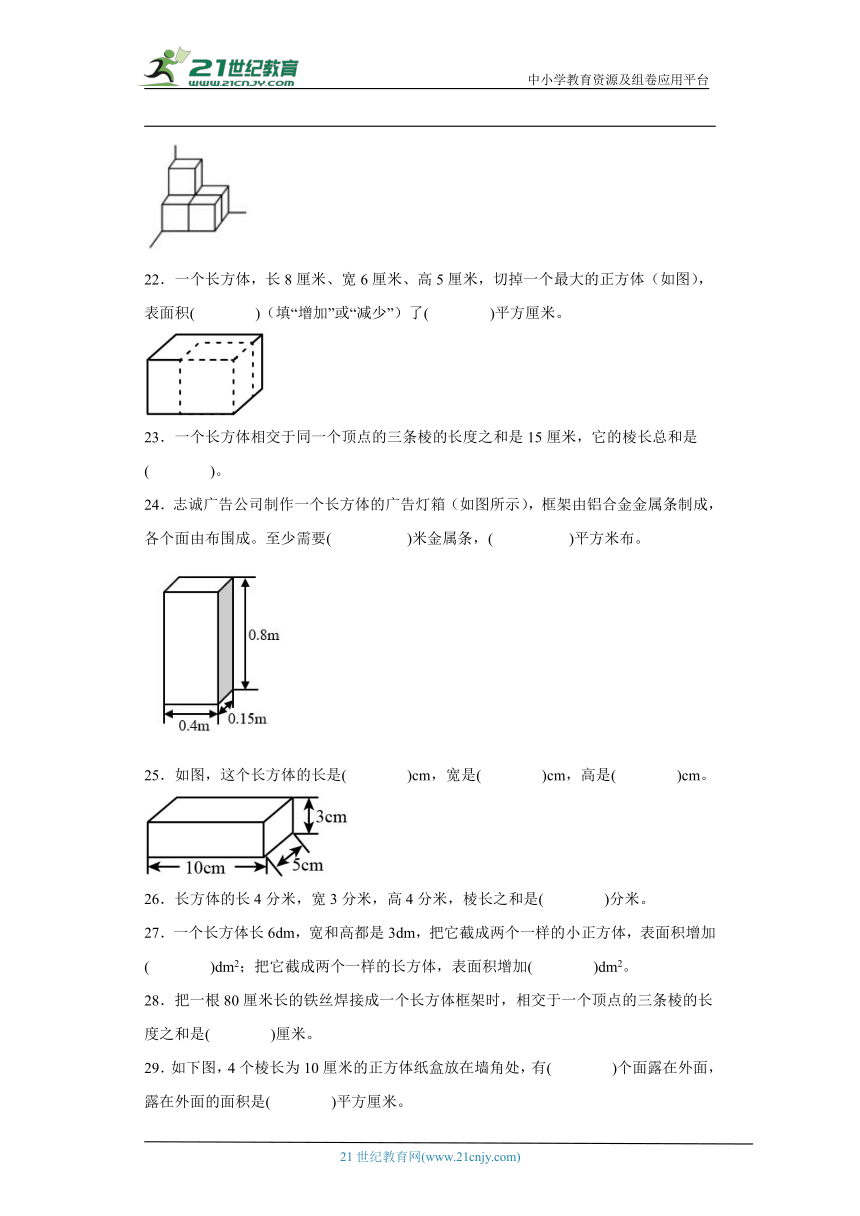
22.一个长方体,长8厘米、宽6厘米、高5厘米,切掉一个最大的正方体(如图),表面积( )(填“增加”或“减少”)了( )平方厘米。
23.一个长方体相交于同一个顶点的三条棱的长度之和是15厘米,它的棱长总和是( )。
24.志诚广告公司制作一个长方体的广告灯箱(如图所示),框架由铝合金金属条制成,各个面由布围成。至少需要( )米金属条,( )平方米布。
25.如图,这个长方体的长是( )cm,宽是( )cm,高是( )cm。
26.长方体的长4分米,宽3分米,高4分米,棱长之和是( )分米。
27.一个长方体长6dm,宽和高都是3dm,把它截成两个一样的小正方体,表面积增加( )dm2;把它截成两个一样的长方体,表面积增加( )dm2。
28.把一根80厘米长的铁丝焊接成一个长方体框架时,相交于一个顶点的三条棱的长度之和是( )厘米。
29.如下图,4个棱长为10厘米的正方体纸盒放在墙角处,有( )个面露在外面,露在外面的面积是( )平方厘米。
30.一个长方体长8cm、宽5cm、高4cm,把它切成三个完全一样的小长方体,表面积最多增加( )cm2。
31.棱长为3cm的正方体,它的棱长总和是( )cm,表面积是( )cm2。
32.一个长方体底面是边长为8cm的正方形,高为20cm,这个长方体的棱长总和是( )cm。
33.如图的长方体是由棱长为1cm的小正方体摆成的,它的长是( )cm,宽是( )cm,高是( )cm。
34.把一个长为10dm、宽为9dm、高为8dm的长方体截成两个一样大小的长方体,则截成的长方体的表面积之和最多比原来增加( )dm2,最少比原来增加( )dm2。
35.在一个棱长是5厘米的正方体的正中打一个边长是2厘米的正方形孔洞(打通),打通后的立体图形表面积是( )平方厘米。
36.把一个长是12厘米、宽是8厘米、高是6厘米的长方体木块表面涂成红色,然后切成棱长是2厘米的小正方体,可以切成( )块小正方体,只有3面涂色的小正方体有( )块,只有2面涂色的小正方体有( )块,只有1面涂色的小正方体有( )块,没有涂色的小正方体有( )块。
37.用下面的五块有机玻璃做成一个无盖的长方体鱼缸,底面应是( )号,制作一个这样的鱼缸需要( )平方分米的玻璃。(接缝处忽略不计)
38.一个长方体的棱长总和是100cm,长是10cm,高是7cm,宽是( )cm。
39.木工师傅用两个长方体材料拼成了一个置物台(如图),这个置物台的表面积是( )平方分米。
40.田田用铁丝围成一个等边三角形,每边长为米,它的周长是( )米。鹏鹏用1米长的铁丝围成一个正方体,这个正方体的棱长是( )米。
41.用两个棱长都是3cm的小正方体拼成一个长方体,拼成的长方体的棱长总和是( )cm,表面积是( )cm2。
42.一个长方体等分成两份,变成了两个小正方体,表面积比原来增加了50平方厘米,原来长方体的表面积是( )平方厘米。
43.一种糖果盒子底面是边长24cm的正方形,高是4.5cm,在外务工的妈妈买了2盒这样的糖果盒子包装在一起寄回去给孩子,至少需要( )的包装纸。
44.有一个长方体,相交于同一顶点的三个面的面积分别是50平方厘米、25平方厘米、30平方厘米,这个长方体的表面积是( )平方厘米。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.3
【分析】长方体有6个面,其中上面和下面、前面和后面、左面和右面分别是一组相对的面。观察下图发现,不能同时看到相对的两个面。从长方体的某个面观察,只能看到1个面;从长方体的某条棱观察,能看到2个面;从长方体的某个顶点观察,能看到3个面。
【详解】长方体有6个面,由于不能同时看到相对的两个面,所以站在一个位置上观察一个长方体,最多能看到3个面。
2. 48 94
【分析】由题意可知,求铁丝的长度就是求长方体的总棱长,根据长方体的总棱长公式:L=(a+b+h)×4,据此代入数值进行计算即可;求塑料板的面积就是求长方体的表面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,据此进行计算即可。
【详解】(5+4+3)×4
=12×4
=48(厘米)
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方厘米)
则做这个框架共要48厘米的铁丝;若在它的表面贴上塑料板,共要94平方厘米塑料板。
3. 95 48
【分析】长方体棱长总和=(长+宽+高)×4,在长方体的6个面中,由较长的长和宽组成的面是面积最大的面。据此可得出答案。
【详解】它的棱长总和为:
(cm)
六个面中最大面积的面是长和宽组成的面,面积为:(cm2)
4.18
【分析】根据正方体的特征,正方体有6个面,每个面的面积相等;把一个正方体锯成两个长方体,增加的表面积即原正方体的两个表面的总面积,表面积增加了6 cm2,所以原正方体一个面的面积为6÷2=3(cm2),由此可计算原正方体的表面积。
【详解】6÷2=3(cm2)
3×6=18(cm2)
所以把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是18cm2。
5. 3 1 8
【分析】观察一个长方体,如果从正面看,一次最少能看到 1个面,如果从某一顶点看,最多能看到3个面;正方体的各个棱长都相等,所以要搭一个正方体,至少需要8个小正方体。
【详解】由分析可知:
观察一个长方体,一次最多看见它的3个面,最少能看到1个面。搭一个正方体,至少需要8个小正方体。
6.148
【分析】将两个长方体拼成一个长方体,表面积减少两个面的面积,要使表面积最小,则减少的面是最大面。由此可知最小的表面积是(5×4+5×3+4×3)×2×2-5×4×2,由此解答。
【详解】(5×4+5×3+4×3)×2×2-5×4×2
=(20+15+12)×2×2-40
=47×2×2-40
=94×2-40
=188-40
=148()
最小的表面积是148。
【点睛】此题考查了长方体的表面积。要求学生熟练掌握并灵活运用。
7.6
【分析】由题意可知:长方体棱长总和是72分米。又长方体棱长总和=(长+宽+高)×4,所以宽=棱长总和÷4-长-高,代入数据计算即可。
【详解】72÷4-7-5
=18-7-5
=6(分米)
它的宽是6分米。
【点睛】本题主要考查长方体有关棱长总和的简单应用,明确长方体棱长总和=(长+宽+高)×4是解题的关键。
8. 275 22
【分析】从正面看露在外面是4个小正方形,从上面看露在外面是3个小正方形,从右面看露在外面是4个小正方形,即露在外面的面一共有:4+3+4=11(个),一个正方形的面积:5×5=25(平方分米),再乘小正方形的个数即可求解;由于搭建一个更大的正方体,更大一点的正方体每条棱长都有3个小正方体组成,即一共需要3×3×3=27(个)小正方体,由于已经有5个,再需要27-5=22(个)即可。
【详解】5×5=25(分米2)
4+3+4
=7+4
=11(个)
25×11=275(分米2)
由于更大的正方体每条棱上是3个小正方体。
3×3×3-5
=9×3-5
=27-5
=22(个)
露在外面的面的面积一共是275分米2,在此基础上要把它堆成一个大正方体,至少还要22个这样的正方体纸箱。
【点睛】本题主要考查组合体的表面积以及正方体的体积公式,熟练掌握正方体的体积公式并灵活运用。
9.84
【分析】正方体有12条棱,并且每条棱的长度相等,所以用“棱长×12”即可求出彩带的长度。
【详解】由分析可知:
12×7=84(dm)
所以需要彩带84dm。
【点睛】本题考查正方体的棱长之和,学生需熟知正方体的特征,以及棱长之和的算法。
10.10
【分析】根据长方体棱长的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱;正方体特征:12条棱长度都相等,据此可以列表解答。
【详解】由分析可得:
一组棱长 一组棱长 一组棱长
第1种 4根3厘米 4根3厘米 4根3厘米
第2种 4根4厘米 4根4厘米 4根4厘米
第3种 4根5厘米 4根5厘米 4根5厘米
第4种 4根5厘米 4根4厘米 4根3厘米
第5种 4根5厘米 4根4厘米 4根4厘米
第6种 4根5厘米 4根3厘米 4根3厘米
第7种 4根4厘米 4根3厘米 4根3厘米
第8种 4根4厘米 4根4厘米 4根3厘米
第9种 4根5厘米 4根5厘米 4根3厘米
第10种 4根5厘米 4根5厘米 4根4厘米
如表,3厘米、4厘米、5厘米长的小棒各有12根,用其中的小棒,可以搭成10种不同形状的长方体(包括正方体)。
【点睛】本题考查了长方体的棱长特征,需要学生可以列举出所有的可能,其中不能漏项,不能重复。
11. 8/八 4/四 正方
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等,12条棱分为互相平行的3组,每组4条棱的长度相等;据此解答。
【详解】一个长方体的长、宽、高分别为10厘米、6厘米、6厘米,那么这个长方体最多有8条棱长度相等,最多有4个面形状相同,剩下的面都是正方形。
【点睛】此题考查的目的是理解掌握长方体的特征。
12. 减少 16
【分析】将3个棱长2分米的正方体拼成一个长方体,会有4个面拼到里面,则这个长方体的表面积比原来3个正方体的表面积之和减少了4个正方形的面积。根据正方形的面积=边长×边长,即可求出减少的面积。
【详解】2×2×4=16(平方分米)
这个长方体的表面积比原来3个正方体的表面积之和减少16平方分米。
【点睛】本题考查立体图形的切拼。明确“3个正方体拼成一个长方体,表面积减少了4个正方形的面积”是解题的关键。
13. 216 72
【分析】根据正方体的特征及正方体的表面积公式:S=6a2,棱长总和=棱长×12,把数据代入公式解答。
【详解】6×6×6
=36×6
=216(cm2)
它的表面积是216cm2。
6×12=72(cm)
棱长之和是72cm。
【点睛】本题主要考查正方体的特征及正方体表面积公式。
14.1550
【分析】求贴瓷砖的面积,就是求这个长方体游泳池5个面的面积和,根据长方体的表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】50×25+(50×2+25×2)×2
=1250+(100+50)×2
=1250+150×2
=1250+300
=1550(平方米)
一个游泳池长50m,宽25m,深2m,在池内四壁及池底贴上瓷砖,贴瓷砖的面积是1550平方米。
【点睛】熟练掌握长方体的表面积公式是解答本题的关键。
15.17
【分析】第一个图形有5个面露在外面,可以写成:4×1+1;第二图形有9个面露在外面,可以写成:4×2+1;第三个图形有13个面露在外面,可以写成:4×3+1;……,第n个图形有4n+1个面露在外面,当n=4时,即可求出露在外面的面的个数。
【详解】根据分析可知,当n=4时:
4×4+1
=16+1
=17(个)
淘气在摆方块,如果按下图中的规律继续往下摆,第4组有17个面露在外面。
【点睛】本题主要考查数与形结合的规律,发现每多1个图就多4个面露在外面是解本题的关键。
16. 6 1 2
【分析】根据正方体展开图的11种特征,此图属于正方形展开图的“2-2-2”型,并且根据正方体展开图的相对面辨别方法:相对的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字两端处的小正方形是正方体的对面,据此判断即可。
【详解】由分析可得:
通过对展开图的观察,1和4在对面,3和6在对面,剩下的2和5在对面。
综上所述:如下图,正方体的展开图上有编号,请你写出相对面的号码:3的相对面是6,4的相对面是1,5的相对面是2。
【点睛】本题考查了正方体展开图的特征,总共分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并且记住规律。
17.200
【分析】把两个棱长是10cm的正方体拼成一个长方体,体积没有改变,但是表面积减少了,减少的面积正好是边长为10cm的两个正方形的面积和,所以减少的面积=边长×边长×2,据此解答即可。
【详解】10×10×2
=100×2
=200(cm2)
把两个棱长都是10cm的正方体拼成一个长方体后,表面积减少了200cm2。
【点睛】立方体的切拼:1、拼起来,表面积减少,体积不变;2、剪切后,表面积增加,体积不变。
18.96
【分析】根据正方体的棱长=棱长之和÷12,计算出正方体的棱长是多少,再根据正方体的表面积=棱长×棱长×6,计算出至少需要多大面积的彩纸。
【详解】48÷12=4(dm)
4×4×6
=16×6
=96(dm2)
至少需要96dm2的彩纸。
【点睛】本题解题关键是根据正方体的棱长=棱长之和÷12,正方体的表面积=棱长×棱长×6,列式计算。
19. 长方体 4/四 78
【分析】这个展开图,有2组相对的面是长方形,1组相对的面是正方形,因此是长方体展开图;且这个立体图形中有4个长方形;
根据长方体相对的面完全一样,找到长方体的长、宽、高,并利用公式:S=(ab+ah+bh)×2,计算其表面积。
【详解】(5×3+3×3+5×3)×2
=(15+9+15)×2
=39×2
=78(平方厘米)
沿虚线可以折叠成一个长方体,这个立体图形中有4个长方形,它的表面积是78平方厘米。
【点睛】本题主要考查了学生的空间想象能力,以及对长方体表面积计算方法的掌握情况。本题可让学生画图,帮助理解题意。
20. 增加 0.02
【分析】在长方体(高1cm)橡皮上挖出一个棱长1cm的正方体,长方体上下两个面比原来减少2个小正方形的面积,同时内部也增加了4个小正方形的面积,所以表面积比原来大2个小正方形的面积。
【详解】1×1×2=2(cm2)
2 cm2=0.02 dm2
所以表面积增加了0.02 dm2。
【点睛】本题考查的关键在于明确切割后的图形表面积增加或减少了哪几个面。并注意单位陷阱,是否需要单位换算。
21. 10 160
【分析】观察题意可知,露在外面的小正方形面有(4+3+3)个,每个面是(4×4)平方厘米,根据乘法的意义,用每个面的面积乘个数,即可求出露在外面的面积。据此解答。
【详解】4+3+3=10(个)
4×4×10=160(平方厘米)
有10个面露在外面,露在外面的面积是160平方厘米。
【点睛】解答本题的关键是数出有几个露在外面的面。
22. 减少 50
【分析】从图形可以看出,切掉的正方体的棱长相当于长方体的高,表面积减少了4个边长为5厘米的正方形,以及增加了2个边长为5厘米的正方形,也就是总共减少了2个边长为5厘米的正方形,根据正方形的面积公式求解即可。
【详解】5×5×2=50(平方厘米)
表面积减少了50平方厘米。
【点睛】本题主要考查了立体图形的切割,注意表面积减少了哪些面。
23.60厘米/60cm
【分析】相交于一个顶点的三条棱分别是长方体的长、宽、高,根据(长+宽+高)×4=长方体的棱长和,用15×4即可求出它的棱长总和。
【详解】15×4=60(厘米)
长方体的棱长总和是60厘米。
【点睛】本题考查了长方体的棱长和公式的灵活应用。
24. 5.4 1
【分析】根据题意,求金属条的长度就是求长方体的棱长之和,求布的面积就是求长方体的表面积。长方体的棱长之和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2,据此代入数据计算。
【详解】(0.4+0.15+0.8)×4
=1.35×4
=5.4(米)
(0.4×0.15+0.4×0.8+0.15×0.8)×2
=(0.06+0.32+0.12)×2
=0.5×2
=1(平方米)
至少需要5.4米金属条,1平方米布。
【点睛】本题考查长方体有关棱长和表面积的应用。掌握长方体棱长之和、表面积的公式是解题的关键。
25. 10 5 3
【分析】长方体每个顶点连接三条棱,三条棱分别叫做长方体的长、宽、高。如下图所示。
【详解】这个长方体的长是10cm,宽是5cm,高是3cm。
【点睛】掌握长方形棱的特点是解题的关键。
26.44
【分析】长方体的棱长之和=(长+宽+高)×4,据此代入数据计算。
【详解】(4+3+4)×4
=11×4
=44(分米)
则棱长之和是44分米。
【点睛】掌握长方体的棱长之和公式是解题的关键。
27. 18 36
【分析】如下图所示,把这个长方形截成两个一样的小正方体,表面积增加了两个边长为3dm的正方形的面积;把它截成两个一样的长方体,表面积增加了两个长6dm,宽3dm的长方形的面积。正方形的面积=边长×边长,长方形的面积=长×宽,据此解答。
【详解】3×3×2=18(dm2)
6×3×2=36(dm2)
把它截成两个一样的小正方体,表面积增加18 dm2;把它截成两个一样的长方体,表面积增加36dm2。
【点睛】本题考查立体图形的切拼。明确切割后表面积增加的部分是解题的关键。
28.20
【分析】根据长方体的特征,长方体的12条棱中互相平行的一组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4,求相交于一个顶点的三条棱的长度之和实质就是求(长+宽+高)的值,由此解答。
【详解】80÷4=20(厘米)
相交于一个顶点的三条棱的长度之和是20厘米。
【点睛】此题主要考查长方体的特征和棱长总和的求法;关键是理解题意。
29. 9/九 900
【分析】有3个正方体露在外面,每个正方体有3个面露在外面,共有9个正方形露在外面,每个正方形的边长是10厘米,根据正方形的面积=边长×边长,即可得解。
【详解】由分析可知:
3×3=9(个)
10×10×9
=100×9
=900(平方厘米)
露出9个面,露在外面的面积是900平方厘米。
【点睛】此题考查规则图形的表面积的计算,解决此题的关键是求出露在外面的面的总个数。
30.160
【分析】把一个长方体切成三个完全一样的小长方体,其表面积增加4个截面的面积,它的上下面的面积最大,据此切成三个完全一样的小长方体,再根据长方形面积公式:面积=长×宽,代入数据,求出一个截面的面积,再乘4,即可解答。
【详解】8×5×4
=40×4
=160(cm2)
一个长方体长8cm、宽5cm、高4cm,把它切成三个完全一样的小长方体,表面积最多增加160cm2。
【点睛】本题考查立体图形的切拼,理解增加面积的组成是解题的关键。
31. 36 54
【分析】根据正方体棱长总和公式:棱长总和=棱长×12,代入数据,求出正方体棱长总和;再根据正方体表面积公式:表面积=棱长×棱长×6,代入数据,即可解答。
【详解】3×12=36(cm)
3×3×6
=9×6
=54(cm2)
棱长为3cm的正方体,它的棱长总和是36cm,表面积是54cm2。
【点睛】熟练掌握正方体棱长总和公式、正方体表面积公式是解答本题的关键。
32.144
【分析】由题意可知长方体的长是8cm,宽是8cm,高是20cm,根据长方体的棱长和=(a+b+h)×4,列式解答即可。
【详解】(8+8+20)×4
=(16+20)×4
=36×4
=144(cm)
这个长方体的棱长总和是144cm。
【点睛】此题主要考查长方体棱长的应用,根据公式解答即可。
33. 4 3 2
【分析】由图示可知,一共有24个小正方体组成,长由几个小正方体组成,就是几cm,同理求得长方体的宽和高,据此解答。
【详解】如图的长方体是由棱长为1cm的小正方体摆成的,它的长是4cm。宽是3cm,高是2cm。
【点睛】本题考查简单的立体图形拼组知识,结合题意分析解答。
34. 180 144
【分析】根据题意可知,把这个长方体截成两个一样大小的长方体,要使表面积增加的最多,也就是与长方体的最大面平行截开,要使表面积增加的最少,也就是与长方体的最小面平行截开,表面积增加两个截面的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】10×9×2
=90×2
=180(dm2)
9×8×2
=72×2
=144(dm2)
截成的长方体的表面积之和最多比原来增加180dm2,最少比原来增加144dm2。
【点睛】此题考查的目的是理解掌握长方体表面积的意义和长方形的面积公式,关键是熟记公式。
35.182
【分析】这个立体图形的表面积等于正方体的表面积减去两个边长是2厘米的正方形面积,再加上4个长是5厘米,宽是2厘米的长方形面积;根据正方形表面积公式:表面积=棱长×棱长×6;正方形面积公式:面积=边长×边长;长方形面积公式:面积=长×宽;代入数据,即可解答。
【详解】5×5×6-2×2×2+5×2×4
=25×6-4×2+10×4
=150-8+40
=142+40
=182(平方厘米)
在一个棱长是5厘米的正方体的正中打一个边长是2厘米的正方形孔洞(打通),打通后的立体图形表面积是182平方厘米。
【点睛】利用正方体表面积公式、正方形面积公式和长方形面积公式进行解答,关键明确打一个空洞,增加的面积与减少的面积。
36. 72 8 28 28 8
【分析】根据长方体切割正方体的特点可得:12÷2=6块,8÷2=4块,6÷2=3块,将各条棱上所得的正方体块数相乘可以求得小正方体的总块数;3面涂色的木块在顶点位置,2面涂色的木块在棱上非顶点的位置,1面涂色的木块在每个面上非棱上的位置,没有涂色的木块用所有小木块的数量减去涂色木块的数量求解。
【详解】12÷2=6(块)
8÷2=4(块)
6÷2=3(块)
可以切成:6×4×3=72(块);
3面涂色的木块在顶点位置,所以只有8块;
2面涂色的木块在棱上非顶点的位置
(6-2)×4+(4-2)×4+(3-2)×4
=4×4+2×4+1×4
=16+8+4
=28(块)
1面涂色的木块在每个面上非棱上的位置
(6-2)×(4-2)×2+(6-2)×(3-2)×2+(4-2)×(3-2)×2
=4×2×2+4×1×2+2×1×2
=16+8+4
=28(块)
没有涂色的数量为:
72-8-28-28=8(块)
【点睛】本题主要考查了染色问题,掌握涂色面数不同的小木块所在位置是本题解题的关键。
37. ③ 108
【分析】长方体对面的面积相等,图中①和④是完全一样的长方形,②和⑤是完全一样的长方形,所以③就是底面;将这5个长方形的面积相加,就是这个鱼缸的表面积。
【详解】用如图所示的五块有机玻璃做成一个无盖的长方体鱼缸,底面应是③号,制作一个这样的鱼缸需要的玻璃:
3×6+3×5×2+5×6×2
= 18+30+60
=108(平方分米)
【点睛】本题考查了长方体表面积的计算,需根据实际确定求是哪几个面的面积和。
38.8
【分析】根据长方体棱长总和公式:棱长总和=(长+宽+高)×4,高=棱长总和÷4-长-宽;代入数据,即可解答。
【详解】100÷4-10-7
=25-10-7
=15-7
=8(cm)
【点睛】熟练掌握长方体棱长总和公式是解答本题的关键。
39.226
【分析】观察图形可知,这个置物台的表面积分为两部分,一部分是长是5分米,宽是4分米,高是7分米的长方体的表面积,另一边部分是长是5分米,宽是4分米,高是2分米长方体的上下两个面的面积与前后两个面的面积和,即4个面的面积和,根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(5×4+5×7+4×7)×2+5×4×2+5×2×2
=(20+35+28)×2+20×2+10×2
=(55+28)×2+40+20
=83×2+40+20
=166+40+20
=206+20
=226(平方分米)
【点睛】解答本题的关键是求这个组合图形的表面积时要去掉重合部分的面积。
40.
【分析】等边三角形,每边长为米,它的周长是3个边长,即×3=米;鹏鹏用1米长的铁丝围成一个正方体,这个正方体有12条棱,它的棱长就是1÷12=米。
【详解】×3=(米)
1÷12=(米)
【点睛】此题考查了三角形的周长和正方体棱长的计算方法,要熟练掌握。
41. 48 90
【分析】拼成的长方体的长、宽、高分别为6厘米、3厘米、3厘米,据此,根据长方体的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,据此代入数值,求出该长方体棱长和;再根据长方体表面积公式:S=2ab+2ah+2bh,代入数值,可求出该长方体的表面积。
【详解】长方体棱长和:
6×4+3×4+3×4
=24+12+12
=36+12
=48(cm)
长方体表面积:
6×3×2+6×3×2+3×3×2
=36+36+18
=72+18
=90(cm2)
【点睛】本题考查了长方体的棱长特征和表面积的相关知识点,熟练的运用公式是解题的关键。
42.250
【分析】根据长方体截成两个相等的正方体,则长方体的表面积就等于小正方体的10个面的面积之和,根据切割的特点,增加了2个面,增加的面积已知,从而可求出一个正方形的面积,再乘10就是原来的长方体的表面积。
【详解】一个小正方形的面积:
50÷2=25(平方厘米)
原来长方体的表面积:
25×10=250(平方厘米)
【点睛】解答此题的关键是根据切割多出来的2个正方形面,求出每个正方形面的面积,再通过空间想象,知道原来的长方体表面积和这些面之间的关系从而解题。
43.2016
【分析】根据题意可知,要想需要包装纸少,就把糖果盒子最大面重合,则重合后的长方体的长是24cm,宽是24cm,高是(4.5×2)cm,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】重合后的长方体的长:24cm;宽:24cm;高4.5×2=9(cm)
(24×24+24×9+24×9)×2
=(576+216+216)×2
=(792+216)×2
=1008×2
=2016(cm2)
【点睛】利用长方体表面积公式进行解答,关键明确,两个长方体最大面积重合,则长方体的表面积最小。
44.210
【分析】长方体表面积是求六个面面积之和。根据计算公式S=(a×b+a×h+b×h)×2。(a表示底面的长,b表示底面的宽,h表示高),依题意可理解为a×b=50平方厘米,a×h=25平方厘米,b×h=30平方厘米,代入即可求出长方体的表面积。
【详解】根据分析得,(50+25+30)×2
=105×2
=210(平方厘米)
【点睛】此题的解题关键是灵活运用长方体的表面积公式解决问题。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
北师大版五年级下册数学第二单元 长方体(一)填空题训练
1.站在固定的位置观察一个长方体,一次最多能看到( )个面。
2.一个长方体框架,长5厘米,宽4厘米,高3厘米,做这个框架共要( )厘米的铁丝;若在它的表面贴上塑料板,共要( )平方厘米塑料板。
3.一个长是8cm、宽是6cm、高是5cm的长方体灯笼,它的棱长总和是( )cm,六个面中最大的面的面积是( )cm2。
4.把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是( ) cm2。
5.观察一个长方体,一次最多看见它的( )个面,最少能看到( )个面。搭一个正方体,至少需要( )个小正方体。
6.用两个长5cm、宽4cm,高3cm的长方体拼成三种不同的长方体,最小的表面积是( )。
7.用一根长72分米的铁丝做一个长7分米,高5分米的长方体框架,它的宽是( )分米。
8.将几个棱长为5分米的正方体纸箱摆放在墙角处(如图),露在外面的面面积是( )分米2,在此基础上要把它堆成一个大正方体,至少还要( )个这样的正方体纸箱。
9.一个正方体的礼品盒,它的棱长是7dm,在所有的棱上粘上彩带,需要彩带( )dm。
10.3厘米、4厘米、5厘米长的小棒各有12根,用其中的小棒,可以搭成( )种不同形状的长方体(包括正方体)。
11.一个长方体的长、宽、高分别为10厘米、6厘米、6厘米,那么这个长方体最多有( )条棱长度相等,最多有( )个面形状相同,剩下的面都是( )形。
12.将3个棱长2分米的正方体拼成一个长方体,这个长方体的表面积比原来3个正方体的表面积之和( )(填“增加”或“减少”)( )平方分米。
13.一个正方体棱长6cm,表面积是( )cm2,棱长之和是( )cm。
14.一个游泳池长50m,宽25m,深2m,在池内四壁及池底贴上瓷砖,贴瓷砖的面积是( )平方米。
15.淘气在摆方块,如果按下图中的规律继续往下摆,第4组有( )个面露在外面。
16.如下图,正方体的展开图上有编号,请你写出相对面的号码:3的相对面是( ),4的相对面是( ),5的相对面是( )。
17.把两个棱长都是10cm的正方体拼成一个长方体后,表面积减少了( )cm2。
18.赵伯伯用一根长48dm的铁丝正好做一个正方体的框架,把它的各个面糊上彩纸,至少需要( )dm2的彩纸。
19.如下图,沿虚线可以折成一个( ),这个立体图形中有( )个长方形,它的表面积是( )平方厘米。(单位:厘米)
20.手工课上,淘气在一块长方体(高lcm)橡皮上挖出一个棱长1cm的正方体(如下图),表面积( )(填“增加”或“减少”)了( )dm2。
21.有5个棱长是4厘米的小正方体堆放在墙角处,有( )个面露在外面,露在外面的面积是( )平方厘米。
22.一个长方体,长8厘米、宽6厘米、高5厘米,切掉一个最大的正方体(如图),表面积( )(填“增加”或“减少”)了( )平方厘米。
23.一个长方体相交于同一个顶点的三条棱的长度之和是15厘米,它的棱长总和是( )。
24.志诚广告公司制作一个长方体的广告灯箱(如图所示),框架由铝合金金属条制成,各个面由布围成。至少需要( )米金属条,( )平方米布。
25.如图,这个长方体的长是( )cm,宽是( )cm,高是( )cm。
26.长方体的长4分米,宽3分米,高4分米,棱长之和是( )分米。
27.一个长方体长6dm,宽和高都是3dm,把它截成两个一样的小正方体,表面积增加( )dm2;把它截成两个一样的长方体,表面积增加( )dm2。
28.把一根80厘米长的铁丝焊接成一个长方体框架时,相交于一个顶点的三条棱的长度之和是( )厘米。
29.如下图,4个棱长为10厘米的正方体纸盒放在墙角处,有( )个面露在外面,露在外面的面积是( )平方厘米。
30.一个长方体长8cm、宽5cm、高4cm,把它切成三个完全一样的小长方体,表面积最多增加( )cm2。
31.棱长为3cm的正方体,它的棱长总和是( )cm,表面积是( )cm2。
32.一个长方体底面是边长为8cm的正方形,高为20cm,这个长方体的棱长总和是( )cm。
33.如图的长方体是由棱长为1cm的小正方体摆成的,它的长是( )cm,宽是( )cm,高是( )cm。
34.把一个长为10dm、宽为9dm、高为8dm的长方体截成两个一样大小的长方体,则截成的长方体的表面积之和最多比原来增加( )dm2,最少比原来增加( )dm2。
35.在一个棱长是5厘米的正方体的正中打一个边长是2厘米的正方形孔洞(打通),打通后的立体图形表面积是( )平方厘米。
36.把一个长是12厘米、宽是8厘米、高是6厘米的长方体木块表面涂成红色,然后切成棱长是2厘米的小正方体,可以切成( )块小正方体,只有3面涂色的小正方体有( )块,只有2面涂色的小正方体有( )块,只有1面涂色的小正方体有( )块,没有涂色的小正方体有( )块。
37.用下面的五块有机玻璃做成一个无盖的长方体鱼缸,底面应是( )号,制作一个这样的鱼缸需要( )平方分米的玻璃。(接缝处忽略不计)
38.一个长方体的棱长总和是100cm,长是10cm,高是7cm,宽是( )cm。
39.木工师傅用两个长方体材料拼成了一个置物台(如图),这个置物台的表面积是( )平方分米。
40.田田用铁丝围成一个等边三角形,每边长为米,它的周长是( )米。鹏鹏用1米长的铁丝围成一个正方体,这个正方体的棱长是( )米。
41.用两个棱长都是3cm的小正方体拼成一个长方体,拼成的长方体的棱长总和是( )cm,表面积是( )cm2。
42.一个长方体等分成两份,变成了两个小正方体,表面积比原来增加了50平方厘米,原来长方体的表面积是( )平方厘米。
43.一种糖果盒子底面是边长24cm的正方形,高是4.5cm,在外务工的妈妈买了2盒这样的糖果盒子包装在一起寄回去给孩子,至少需要( )的包装纸。
44.有一个长方体,相交于同一顶点的三个面的面积分别是50平方厘米、25平方厘米、30平方厘米,这个长方体的表面积是( )平方厘米。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.3
【分析】长方体有6个面,其中上面和下面、前面和后面、左面和右面分别是一组相对的面。观察下图发现,不能同时看到相对的两个面。从长方体的某个面观察,只能看到1个面;从长方体的某条棱观察,能看到2个面;从长方体的某个顶点观察,能看到3个面。
【详解】长方体有6个面,由于不能同时看到相对的两个面,所以站在一个位置上观察一个长方体,最多能看到3个面。
2. 48 94
【分析】由题意可知,求铁丝的长度就是求长方体的总棱长,根据长方体的总棱长公式:L=(a+b+h)×4,据此代入数值进行计算即可;求塑料板的面积就是求长方体的表面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,据此进行计算即可。
【详解】(5+4+3)×4
=12×4
=48(厘米)
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方厘米)
则做这个框架共要48厘米的铁丝;若在它的表面贴上塑料板,共要94平方厘米塑料板。
3. 95 48
【分析】长方体棱长总和=(长+宽+高)×4,在长方体的6个面中,由较长的长和宽组成的面是面积最大的面。据此可得出答案。
【详解】它的棱长总和为:
(cm)
六个面中最大面积的面是长和宽组成的面,面积为:(cm2)
4.18
【分析】根据正方体的特征,正方体有6个面,每个面的面积相等;把一个正方体锯成两个长方体,增加的表面积即原正方体的两个表面的总面积,表面积增加了6 cm2,所以原正方体一个面的面积为6÷2=3(cm2),由此可计算原正方体的表面积。
【详解】6÷2=3(cm2)
3×6=18(cm2)
所以把一个正方体锯成两个长方体,表面积增加了6cm2,那么原正方体的表面积是18cm2。
5. 3 1 8
【分析】观察一个长方体,如果从正面看,一次最少能看到 1个面,如果从某一顶点看,最多能看到3个面;正方体的各个棱长都相等,所以要搭一个正方体,至少需要8个小正方体。
【详解】由分析可知:
观察一个长方体,一次最多看见它的3个面,最少能看到1个面。搭一个正方体,至少需要8个小正方体。
6.148
【分析】将两个长方体拼成一个长方体,表面积减少两个面的面积,要使表面积最小,则减少的面是最大面。由此可知最小的表面积是(5×4+5×3+4×3)×2×2-5×4×2,由此解答。
【详解】(5×4+5×3+4×3)×2×2-5×4×2
=(20+15+12)×2×2-40
=47×2×2-40
=94×2-40
=188-40
=148()
最小的表面积是148。
【点睛】此题考查了长方体的表面积。要求学生熟练掌握并灵活运用。
7.6
【分析】由题意可知:长方体棱长总和是72分米。又长方体棱长总和=(长+宽+高)×4,所以宽=棱长总和÷4-长-高,代入数据计算即可。
【详解】72÷4-7-5
=18-7-5
=6(分米)
它的宽是6分米。
【点睛】本题主要考查长方体有关棱长总和的简单应用,明确长方体棱长总和=(长+宽+高)×4是解题的关键。
8. 275 22
【分析】从正面看露在外面是4个小正方形,从上面看露在外面是3个小正方形,从右面看露在外面是4个小正方形,即露在外面的面一共有:4+3+4=11(个),一个正方形的面积:5×5=25(平方分米),再乘小正方形的个数即可求解;由于搭建一个更大的正方体,更大一点的正方体每条棱长都有3个小正方体组成,即一共需要3×3×3=27(个)小正方体,由于已经有5个,再需要27-5=22(个)即可。
【详解】5×5=25(分米2)
4+3+4
=7+4
=11(个)
25×11=275(分米2)
由于更大的正方体每条棱上是3个小正方体。
3×3×3-5
=9×3-5
=27-5
=22(个)
露在外面的面的面积一共是275分米2,在此基础上要把它堆成一个大正方体,至少还要22个这样的正方体纸箱。
【点睛】本题主要考查组合体的表面积以及正方体的体积公式,熟练掌握正方体的体积公式并灵活运用。
9.84
【分析】正方体有12条棱,并且每条棱的长度相等,所以用“棱长×12”即可求出彩带的长度。
【详解】由分析可知:
12×7=84(dm)
所以需要彩带84dm。
【点睛】本题考查正方体的棱长之和,学生需熟知正方体的特征,以及棱长之和的算法。
10.10
【分析】根据长方体棱长的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱;正方体特征:12条棱长度都相等,据此可以列表解答。
【详解】由分析可得:
一组棱长 一组棱长 一组棱长
第1种 4根3厘米 4根3厘米 4根3厘米
第2种 4根4厘米 4根4厘米 4根4厘米
第3种 4根5厘米 4根5厘米 4根5厘米
第4种 4根5厘米 4根4厘米 4根3厘米
第5种 4根5厘米 4根4厘米 4根4厘米
第6种 4根5厘米 4根3厘米 4根3厘米
第7种 4根4厘米 4根3厘米 4根3厘米
第8种 4根4厘米 4根4厘米 4根3厘米
第9种 4根5厘米 4根5厘米 4根3厘米
第10种 4根5厘米 4根5厘米 4根4厘米
如表,3厘米、4厘米、5厘米长的小棒各有12根,用其中的小棒,可以搭成10种不同形状的长方体(包括正方体)。
【点睛】本题考查了长方体的棱长特征,需要学生可以列举出所有的可能,其中不能漏项,不能重复。
11. 8/八 4/四 正方
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等,12条棱分为互相平行的3组,每组4条棱的长度相等;据此解答。
【详解】一个长方体的长、宽、高分别为10厘米、6厘米、6厘米,那么这个长方体最多有8条棱长度相等,最多有4个面形状相同,剩下的面都是正方形。
【点睛】此题考查的目的是理解掌握长方体的特征。
12. 减少 16
【分析】将3个棱长2分米的正方体拼成一个长方体,会有4个面拼到里面,则这个长方体的表面积比原来3个正方体的表面积之和减少了4个正方形的面积。根据正方形的面积=边长×边长,即可求出减少的面积。
【详解】2×2×4=16(平方分米)
这个长方体的表面积比原来3个正方体的表面积之和减少16平方分米。
【点睛】本题考查立体图形的切拼。明确“3个正方体拼成一个长方体,表面积减少了4个正方形的面积”是解题的关键。
13. 216 72
【分析】根据正方体的特征及正方体的表面积公式:S=6a2,棱长总和=棱长×12,把数据代入公式解答。
【详解】6×6×6
=36×6
=216(cm2)
它的表面积是216cm2。
6×12=72(cm)
棱长之和是72cm。
【点睛】本题主要考查正方体的特征及正方体表面积公式。
14.1550
【分析】求贴瓷砖的面积,就是求这个长方体游泳池5个面的面积和,根据长方体的表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】50×25+(50×2+25×2)×2
=1250+(100+50)×2
=1250+150×2
=1250+300
=1550(平方米)
一个游泳池长50m,宽25m,深2m,在池内四壁及池底贴上瓷砖,贴瓷砖的面积是1550平方米。
【点睛】熟练掌握长方体的表面积公式是解答本题的关键。
15.17
【分析】第一个图形有5个面露在外面,可以写成:4×1+1;第二图形有9个面露在外面,可以写成:4×2+1;第三个图形有13个面露在外面,可以写成:4×3+1;……,第n个图形有4n+1个面露在外面,当n=4时,即可求出露在外面的面的个数。
【详解】根据分析可知,当n=4时:
4×4+1
=16+1
=17(个)
淘气在摆方块,如果按下图中的规律继续往下摆,第4组有17个面露在外面。
【点睛】本题主要考查数与形结合的规律,发现每多1个图就多4个面露在外面是解本题的关键。
16. 6 1 2
【分析】根据正方体展开图的11种特征,此图属于正方形展开图的“2-2-2”型,并且根据正方体展开图的相对面辨别方法:相对的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字两端处的小正方形是正方体的对面,据此判断即可。
【详解】由分析可得:
通过对展开图的观察,1和4在对面,3和6在对面,剩下的2和5在对面。
综上所述:如下图,正方体的展开图上有编号,请你写出相对面的号码:3的相对面是6,4的相对面是1,5的相对面是2。
【点睛】本题考查了正方体展开图的特征,总共分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并且记住规律。
17.200
【分析】把两个棱长是10cm的正方体拼成一个长方体,体积没有改变,但是表面积减少了,减少的面积正好是边长为10cm的两个正方形的面积和,所以减少的面积=边长×边长×2,据此解答即可。
【详解】10×10×2
=100×2
=200(cm2)
把两个棱长都是10cm的正方体拼成一个长方体后,表面积减少了200cm2。
【点睛】立方体的切拼:1、拼起来,表面积减少,体积不变;2、剪切后,表面积增加,体积不变。
18.96
【分析】根据正方体的棱长=棱长之和÷12,计算出正方体的棱长是多少,再根据正方体的表面积=棱长×棱长×6,计算出至少需要多大面积的彩纸。
【详解】48÷12=4(dm)
4×4×6
=16×6
=96(dm2)
至少需要96dm2的彩纸。
【点睛】本题解题关键是根据正方体的棱长=棱长之和÷12,正方体的表面积=棱长×棱长×6,列式计算。
19. 长方体 4/四 78
【分析】这个展开图,有2组相对的面是长方形,1组相对的面是正方形,因此是长方体展开图;且这个立体图形中有4个长方形;
根据长方体相对的面完全一样,找到长方体的长、宽、高,并利用公式:S=(ab+ah+bh)×2,计算其表面积。
【详解】(5×3+3×3+5×3)×2
=(15+9+15)×2
=39×2
=78(平方厘米)
沿虚线可以折叠成一个长方体,这个立体图形中有4个长方形,它的表面积是78平方厘米。
【点睛】本题主要考查了学生的空间想象能力,以及对长方体表面积计算方法的掌握情况。本题可让学生画图,帮助理解题意。
20. 增加 0.02
【分析】在长方体(高1cm)橡皮上挖出一个棱长1cm的正方体,长方体上下两个面比原来减少2个小正方形的面积,同时内部也增加了4个小正方形的面积,所以表面积比原来大2个小正方形的面积。
【详解】1×1×2=2(cm2)
2 cm2=0.02 dm2
所以表面积增加了0.02 dm2。
【点睛】本题考查的关键在于明确切割后的图形表面积增加或减少了哪几个面。并注意单位陷阱,是否需要单位换算。
21. 10 160
【分析】观察题意可知,露在外面的小正方形面有(4+3+3)个,每个面是(4×4)平方厘米,根据乘法的意义,用每个面的面积乘个数,即可求出露在外面的面积。据此解答。
【详解】4+3+3=10(个)
4×4×10=160(平方厘米)
有10个面露在外面,露在外面的面积是160平方厘米。
【点睛】解答本题的关键是数出有几个露在外面的面。
22. 减少 50
【分析】从图形可以看出,切掉的正方体的棱长相当于长方体的高,表面积减少了4个边长为5厘米的正方形,以及增加了2个边长为5厘米的正方形,也就是总共减少了2个边长为5厘米的正方形,根据正方形的面积公式求解即可。
【详解】5×5×2=50(平方厘米)
表面积减少了50平方厘米。
【点睛】本题主要考查了立体图形的切割,注意表面积减少了哪些面。
23.60厘米/60cm
【分析】相交于一个顶点的三条棱分别是长方体的长、宽、高,根据(长+宽+高)×4=长方体的棱长和,用15×4即可求出它的棱长总和。
【详解】15×4=60(厘米)
长方体的棱长总和是60厘米。
【点睛】本题考查了长方体的棱长和公式的灵活应用。
24. 5.4 1
【分析】根据题意,求金属条的长度就是求长方体的棱长之和,求布的面积就是求长方体的表面积。长方体的棱长之和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2,据此代入数据计算。
【详解】(0.4+0.15+0.8)×4
=1.35×4
=5.4(米)
(0.4×0.15+0.4×0.8+0.15×0.8)×2
=(0.06+0.32+0.12)×2
=0.5×2
=1(平方米)
至少需要5.4米金属条,1平方米布。
【点睛】本题考查长方体有关棱长和表面积的应用。掌握长方体棱长之和、表面积的公式是解题的关键。
25. 10 5 3
【分析】长方体每个顶点连接三条棱,三条棱分别叫做长方体的长、宽、高。如下图所示。
【详解】这个长方体的长是10cm,宽是5cm,高是3cm。
【点睛】掌握长方形棱的特点是解题的关键。
26.44
【分析】长方体的棱长之和=(长+宽+高)×4,据此代入数据计算。
【详解】(4+3+4)×4
=11×4
=44(分米)
则棱长之和是44分米。
【点睛】掌握长方体的棱长之和公式是解题的关键。
27. 18 36
【分析】如下图所示,把这个长方形截成两个一样的小正方体,表面积增加了两个边长为3dm的正方形的面积;把它截成两个一样的长方体,表面积增加了两个长6dm,宽3dm的长方形的面积。正方形的面积=边长×边长,长方形的面积=长×宽,据此解答。
【详解】3×3×2=18(dm2)
6×3×2=36(dm2)
把它截成两个一样的小正方体,表面积增加18 dm2;把它截成两个一样的长方体,表面积增加36dm2。
【点睛】本题考查立体图形的切拼。明确切割后表面积增加的部分是解题的关键。
28.20
【分析】根据长方体的特征,长方体的12条棱中互相平行的一组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4,求相交于一个顶点的三条棱的长度之和实质就是求(长+宽+高)的值,由此解答。
【详解】80÷4=20(厘米)
相交于一个顶点的三条棱的长度之和是20厘米。
【点睛】此题主要考查长方体的特征和棱长总和的求法;关键是理解题意。
29. 9/九 900
【分析】有3个正方体露在外面,每个正方体有3个面露在外面,共有9个正方形露在外面,每个正方形的边长是10厘米,根据正方形的面积=边长×边长,即可得解。
【详解】由分析可知:
3×3=9(个)
10×10×9
=100×9
=900(平方厘米)
露出9个面,露在外面的面积是900平方厘米。
【点睛】此题考查规则图形的表面积的计算,解决此题的关键是求出露在外面的面的总个数。
30.160
【分析】把一个长方体切成三个完全一样的小长方体,其表面积增加4个截面的面积,它的上下面的面积最大,据此切成三个完全一样的小长方体,再根据长方形面积公式:面积=长×宽,代入数据,求出一个截面的面积,再乘4,即可解答。
【详解】8×5×4
=40×4
=160(cm2)
一个长方体长8cm、宽5cm、高4cm,把它切成三个完全一样的小长方体,表面积最多增加160cm2。
【点睛】本题考查立体图形的切拼,理解增加面积的组成是解题的关键。
31. 36 54
【分析】根据正方体棱长总和公式:棱长总和=棱长×12,代入数据,求出正方体棱长总和;再根据正方体表面积公式:表面积=棱长×棱长×6,代入数据,即可解答。
【详解】3×12=36(cm)
3×3×6
=9×6
=54(cm2)
棱长为3cm的正方体,它的棱长总和是36cm,表面积是54cm2。
【点睛】熟练掌握正方体棱长总和公式、正方体表面积公式是解答本题的关键。
32.144
【分析】由题意可知长方体的长是8cm,宽是8cm,高是20cm,根据长方体的棱长和=(a+b+h)×4,列式解答即可。
【详解】(8+8+20)×4
=(16+20)×4
=36×4
=144(cm)
这个长方体的棱长总和是144cm。
【点睛】此题主要考查长方体棱长的应用,根据公式解答即可。
33. 4 3 2
【分析】由图示可知,一共有24个小正方体组成,长由几个小正方体组成,就是几cm,同理求得长方体的宽和高,据此解答。
【详解】如图的长方体是由棱长为1cm的小正方体摆成的,它的长是4cm。宽是3cm,高是2cm。
【点睛】本题考查简单的立体图形拼组知识,结合题意分析解答。
34. 180 144
【分析】根据题意可知,把这个长方体截成两个一样大小的长方体,要使表面积增加的最多,也就是与长方体的最大面平行截开,要使表面积增加的最少,也就是与长方体的最小面平行截开,表面积增加两个截面的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】10×9×2
=90×2
=180(dm2)
9×8×2
=72×2
=144(dm2)
截成的长方体的表面积之和最多比原来增加180dm2,最少比原来增加144dm2。
【点睛】此题考查的目的是理解掌握长方体表面积的意义和长方形的面积公式,关键是熟记公式。
35.182
【分析】这个立体图形的表面积等于正方体的表面积减去两个边长是2厘米的正方形面积,再加上4个长是5厘米,宽是2厘米的长方形面积;根据正方形表面积公式:表面积=棱长×棱长×6;正方形面积公式:面积=边长×边长;长方形面积公式:面积=长×宽;代入数据,即可解答。
【详解】5×5×6-2×2×2+5×2×4
=25×6-4×2+10×4
=150-8+40
=142+40
=182(平方厘米)
在一个棱长是5厘米的正方体的正中打一个边长是2厘米的正方形孔洞(打通),打通后的立体图形表面积是182平方厘米。
【点睛】利用正方体表面积公式、正方形面积公式和长方形面积公式进行解答,关键明确打一个空洞,增加的面积与减少的面积。
36. 72 8 28 28 8
【分析】根据长方体切割正方体的特点可得:12÷2=6块,8÷2=4块,6÷2=3块,将各条棱上所得的正方体块数相乘可以求得小正方体的总块数;3面涂色的木块在顶点位置,2面涂色的木块在棱上非顶点的位置,1面涂色的木块在每个面上非棱上的位置,没有涂色的木块用所有小木块的数量减去涂色木块的数量求解。
【详解】12÷2=6(块)
8÷2=4(块)
6÷2=3(块)
可以切成:6×4×3=72(块);
3面涂色的木块在顶点位置,所以只有8块;
2面涂色的木块在棱上非顶点的位置
(6-2)×4+(4-2)×4+(3-2)×4
=4×4+2×4+1×4
=16+8+4
=28(块)
1面涂色的木块在每个面上非棱上的位置
(6-2)×(4-2)×2+(6-2)×(3-2)×2+(4-2)×(3-2)×2
=4×2×2+4×1×2+2×1×2
=16+8+4
=28(块)
没有涂色的数量为:
72-8-28-28=8(块)
【点睛】本题主要考查了染色问题,掌握涂色面数不同的小木块所在位置是本题解题的关键。
37. ③ 108
【分析】长方体对面的面积相等,图中①和④是完全一样的长方形,②和⑤是完全一样的长方形,所以③就是底面;将这5个长方形的面积相加,就是这个鱼缸的表面积。
【详解】用如图所示的五块有机玻璃做成一个无盖的长方体鱼缸,底面应是③号,制作一个这样的鱼缸需要的玻璃:
3×6+3×5×2+5×6×2
= 18+30+60
=108(平方分米)
【点睛】本题考查了长方体表面积的计算,需根据实际确定求是哪几个面的面积和。
38.8
【分析】根据长方体棱长总和公式:棱长总和=(长+宽+高)×4,高=棱长总和÷4-长-宽;代入数据,即可解答。
【详解】100÷4-10-7
=25-10-7
=15-7
=8(cm)
【点睛】熟练掌握长方体棱长总和公式是解答本题的关键。
39.226
【分析】观察图形可知,这个置物台的表面积分为两部分,一部分是长是5分米,宽是4分米,高是7分米的长方体的表面积,另一边部分是长是5分米,宽是4分米,高是2分米长方体的上下两个面的面积与前后两个面的面积和,即4个面的面积和,根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(5×4+5×7+4×7)×2+5×4×2+5×2×2
=(20+35+28)×2+20×2+10×2
=(55+28)×2+40+20
=83×2+40+20
=166+40+20
=206+20
=226(平方分米)
【点睛】解答本题的关键是求这个组合图形的表面积时要去掉重合部分的面积。
40.
【分析】等边三角形,每边长为米,它的周长是3个边长,即×3=米;鹏鹏用1米长的铁丝围成一个正方体,这个正方体有12条棱,它的棱长就是1÷12=米。
【详解】×3=(米)
1÷12=(米)
【点睛】此题考查了三角形的周长和正方体棱长的计算方法,要熟练掌握。
41. 48 90
【分析】拼成的长方体的长、宽、高分别为6厘米、3厘米、3厘米,据此,根据长方体的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,据此代入数值,求出该长方体棱长和;再根据长方体表面积公式:S=2ab+2ah+2bh,代入数值,可求出该长方体的表面积。
【详解】长方体棱长和:
6×4+3×4+3×4
=24+12+12
=36+12
=48(cm)
长方体表面积:
6×3×2+6×3×2+3×3×2
=36+36+18
=72+18
=90(cm2)
【点睛】本题考查了长方体的棱长特征和表面积的相关知识点,熟练的运用公式是解题的关键。
42.250
【分析】根据长方体截成两个相等的正方体,则长方体的表面积就等于小正方体的10个面的面积之和,根据切割的特点,增加了2个面,增加的面积已知,从而可求出一个正方形的面积,再乘10就是原来的长方体的表面积。
【详解】一个小正方形的面积:
50÷2=25(平方厘米)
原来长方体的表面积:
25×10=250(平方厘米)
【点睛】解答此题的关键是根据切割多出来的2个正方形面,求出每个正方形面的面积,再通过空间想象,知道原来的长方体表面积和这些面之间的关系从而解题。
43.2016
【分析】根据题意可知,要想需要包装纸少,就把糖果盒子最大面重合,则重合后的长方体的长是24cm,宽是24cm,高是(4.5×2)cm,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】重合后的长方体的长:24cm;宽:24cm;高4.5×2=9(cm)
(24×24+24×9+24×9)×2
=(576+216+216)×2
=(792+216)×2
=1008×2
=2016(cm2)
【点睛】利用长方体表面积公式进行解答,关键明确,两个长方体最大面积重合,则长方体的表面积最小。
44.210
【分析】长方体表面积是求六个面面积之和。根据计算公式S=(a×b+a×h+b×h)×2。(a表示底面的长,b表示底面的宽,h表示高),依题意可理解为a×b=50平方厘米,a×h=25平方厘米,b×h=30平方厘米,代入即可求出长方体的表面积。
【详解】根据分析得,(50+25+30)×2
=105×2
=210(平方厘米)
【点睛】此题的解题关键是灵活运用长方体的表面积公式解决问题。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
