人教版八年级数学下册第17章《勾股定理》单元小练习 (含答案)
文档属性
| 名称 | 人教版八年级数学下册第17章《勾股定理》单元小练习 (含答案) | 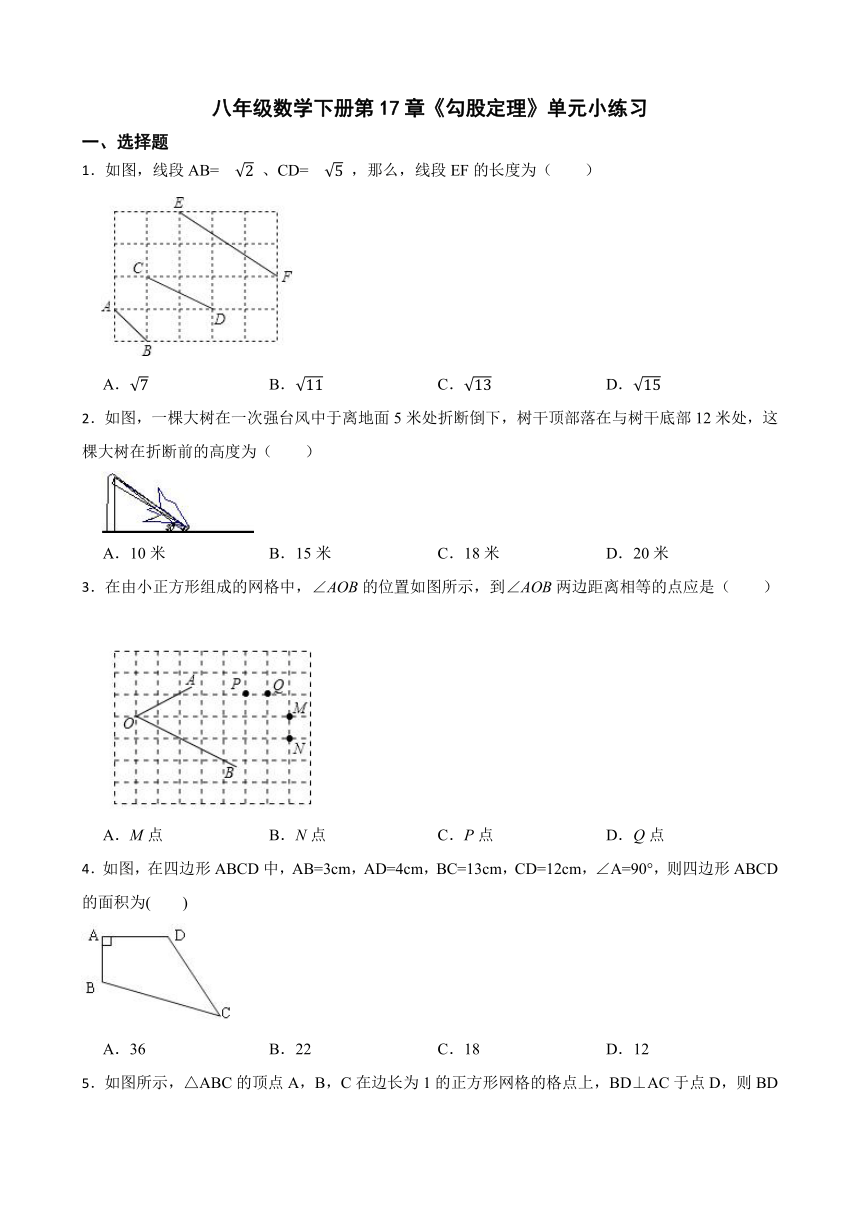 | |
| 格式 | docx | ||
| 文件大小 | 117.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 10:56:13 | ||
图片预览


文档简介
八年级数学下册第17章《勾股定理》单元小练习
一、选择题
1.如图,线段AB= 、CD= ,那么,线段EF的长度为( )
A. B. C. D.
2.如图,一棵大树在一次强台风中于离地面5米处折断倒下,树干顶部落在与树干底部12米处,这棵大树在折断前的高度为( )
A.10米 B.15米 C.18米 D.20米
3.在由小正方形组成的网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
4.如图,在四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,则四边形ABCD的面积为( )
A.36 B.22 C.18 D.12
5.如图所示,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
6.在矩形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为( )
A.8cm B.6cm C.4cm D.2cm
7.如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( )
A.4 B.6 C.16 D.55
二、填空题
8.如图,等腰RtABC中,∠ABC=90°,O是ABC内一点,OA=6,OB=,OC=10,为ABC外一点,且CBO≌AB,则四边形的面积为 .
9.如图,将矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上点P处,已知 ,PM=3,PN=4,那么矩形纸片ABCD的面积为 .
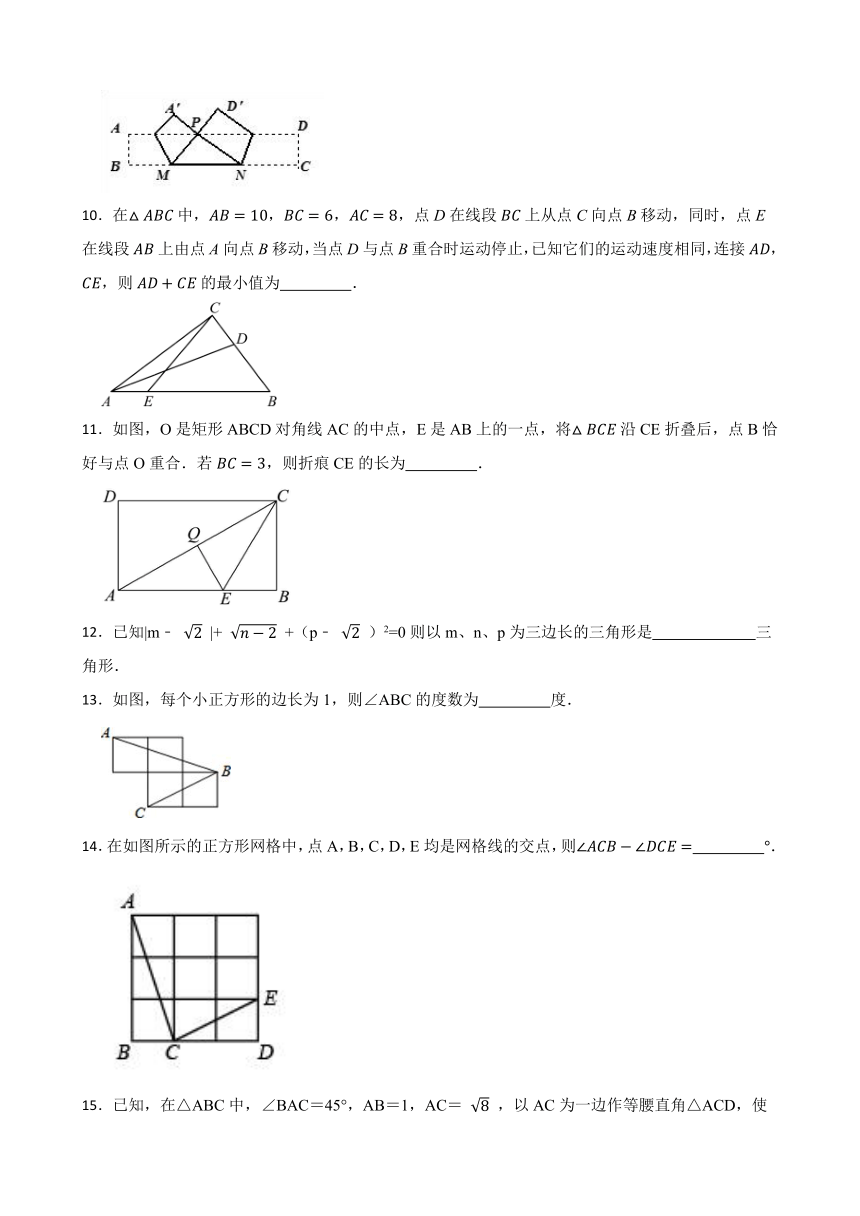
10.在中,,,,点D在线段上从点C向点B移动,同时,点E在线段上由点A向点B移动,当点D与点B重合时运动停止,已知它们的运动速度相同,连接,,则的最小值为 .
11.如图,O是矩形ABCD对角线AC的中点,E是AB上的一点,将沿CE折叠后,点B恰好与点O重合.若,则折痕CE的长为 .
12.已知|m﹣ |+ +(p﹣ )2=0则以m、n、p为三边长的三角形是 三角形.
13.如图,每个小正方形的边长为1,则∠ABC的度数为 度.
14.在如图所示的正方形网格中,点A,B,C,D,E均是网格线的交点,则 .
15.已知,在△ABC中,∠BAC=45°,AB=1,AC= ,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为 .
16.如图,在高,斜坡长,宽为2m的楼梯表面铺地毯,则地毯的面积至少需要 .
三、解答题
17.已知,在△ABC中,AD⊥BC,垂足为点D,AB=15,AD=12,AC=13,求△ABC面积.
18.如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P,沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上.小岛A离港口P有多少海里?
19.如图,从电线杆离地面的点处向地面拉一条长的钢索,,这条钢索在地面的固定点到电线杆底部点的距离是多少?
20.在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上另一停靠站B的距离为400米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否而需要暂时封锁?请通过计算进行说明.
答案解析部分
1.C
2.C
3.A
4.A
5.A
6.C
7.C
8.40
9.
10.
11.
12.等腰直角
13.45
14.45
15. 或
16.14
17.解:∵AD⊥BC,
∴由勾股定理得,BD= = =9,
CD= = =5,
点D在BC上时,BC=BD+CD=9+5=14,
△ABC的面积= ×14×12=84,
点D不在BC上时,BC=BD﹣CD=9﹣5=4,
△ABC的面积= ×4×12=24.
所以,△ABC的面积为24或84
18.解:过点A作AD⊥PB于点D,
根据题意得: (海里)
设BD=x,则 ,
∴ ,
解得:
∴
∵ ,
∴
解得, .
19.解:地面、电线杆、钢索恰好构成直角三角形,,,.
答:这条钢索在地面的固定点到电线杆底部点的距离是.
20.解:过C作CD⊥AB于D.根据BC=400米,AC=300米,∠ACB=90°,利用根据勾股定理有AB=500米.利用S△ABC= 得到CD=240米.再根据240米<250米可以判断有危险.
一、选择题
1.如图,线段AB= 、CD= ,那么,线段EF的长度为( )
A. B. C. D.
2.如图,一棵大树在一次强台风中于离地面5米处折断倒下,树干顶部落在与树干底部12米处,这棵大树在折断前的高度为( )
A.10米 B.15米 C.18米 D.20米
3.在由小正方形组成的网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
4.如图,在四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,则四边形ABCD的面积为( )
A.36 B.22 C.18 D.12
5.如图所示,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
6.在矩形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为( )
A.8cm B.6cm C.4cm D.2cm
7.如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( )
A.4 B.6 C.16 D.55
二、填空题
8.如图,等腰RtABC中,∠ABC=90°,O是ABC内一点,OA=6,OB=,OC=10,为ABC外一点,且CBO≌AB,则四边形的面积为 .
9.如图,将矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上点P处,已知 ,PM=3,PN=4,那么矩形纸片ABCD的面积为 .
10.在中,,,,点D在线段上从点C向点B移动,同时,点E在线段上由点A向点B移动,当点D与点B重合时运动停止,已知它们的运动速度相同,连接,,则的最小值为 .
11.如图,O是矩形ABCD对角线AC的中点,E是AB上的一点,将沿CE折叠后,点B恰好与点O重合.若,则折痕CE的长为 .
12.已知|m﹣ |+ +(p﹣ )2=0则以m、n、p为三边长的三角形是 三角形.
13.如图,每个小正方形的边长为1,则∠ABC的度数为 度.
14.在如图所示的正方形网格中,点A,B,C,D,E均是网格线的交点,则 .
15.已知,在△ABC中,∠BAC=45°,AB=1,AC= ,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为 .
16.如图,在高,斜坡长,宽为2m的楼梯表面铺地毯,则地毯的面积至少需要 .
三、解答题
17.已知,在△ABC中,AD⊥BC,垂足为点D,AB=15,AD=12,AC=13,求△ABC面积.
18.如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P,沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上.小岛A离港口P有多少海里?
19.如图,从电线杆离地面的点处向地面拉一条长的钢索,,这条钢索在地面的固定点到电线杆底部点的距离是多少?
20.在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上另一停靠站B的距离为400米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否而需要暂时封锁?请通过计算进行说明.
答案解析部分
1.C
2.C
3.A
4.A
5.A
6.C
7.C
8.40
9.
10.
11.
12.等腰直角
13.45
14.45
15. 或
16.14
17.解:∵AD⊥BC,
∴由勾股定理得,BD= = =9,
CD= = =5,
点D在BC上时,BC=BD+CD=9+5=14,
△ABC的面积= ×14×12=84,
点D不在BC上时,BC=BD﹣CD=9﹣5=4,
△ABC的面积= ×4×12=24.
所以,△ABC的面积为24或84
18.解:过点A作AD⊥PB于点D,
根据题意得: (海里)
设BD=x,则 ,
∴ ,
解得:
∴
∵ ,
∴
解得, .
19.解:地面、电线杆、钢索恰好构成直角三角形,,,.
答:这条钢索在地面的固定点到电线杆底部点的距离是.
20.解:过C作CD⊥AB于D.根据BC=400米,AC=300米,∠ACB=90°,利用根据勾股定理有AB=500米.利用S△ABC= 得到CD=240米.再根据240米<250米可以判断有危险.
