18.2.1 矩形的性质(第一课时)【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 18.2.1 矩形的性质(第一课时)【2024春人教八下数学同步优质教案】 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 21:48:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
18.2.1 矩形的性质 教学设计
一、教学目标:
1.理解矩形的概念,知道矩形与平行四边形的区别与联系.
2.会证明矩形的性质,会用矩形的性质解决简单的问题.
3.掌握直角三角形斜边中线的性质,并会简单的运用.
二、教学重、难点:
重点:理解并掌握矩形的性质定理及推论,会用矩形的性质定理及推论进行推导证明.
难点:会综合运用矩形的性质定理、推论以及特殊三角形的性质进行证明与计算.
三、教学过程:
复习回顾
平行四边形的定义,及其边,角,对角线都有哪些性质呢?
定义:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行;即:AD∥BC,AB∥CD
对边相等;即:AB=DC,AD=BC
对角相等;即:∠DAB=∠BCD,∠ABC=∠CDA
对角线互相平分.即:AO=CO,BO=DO
知识精讲
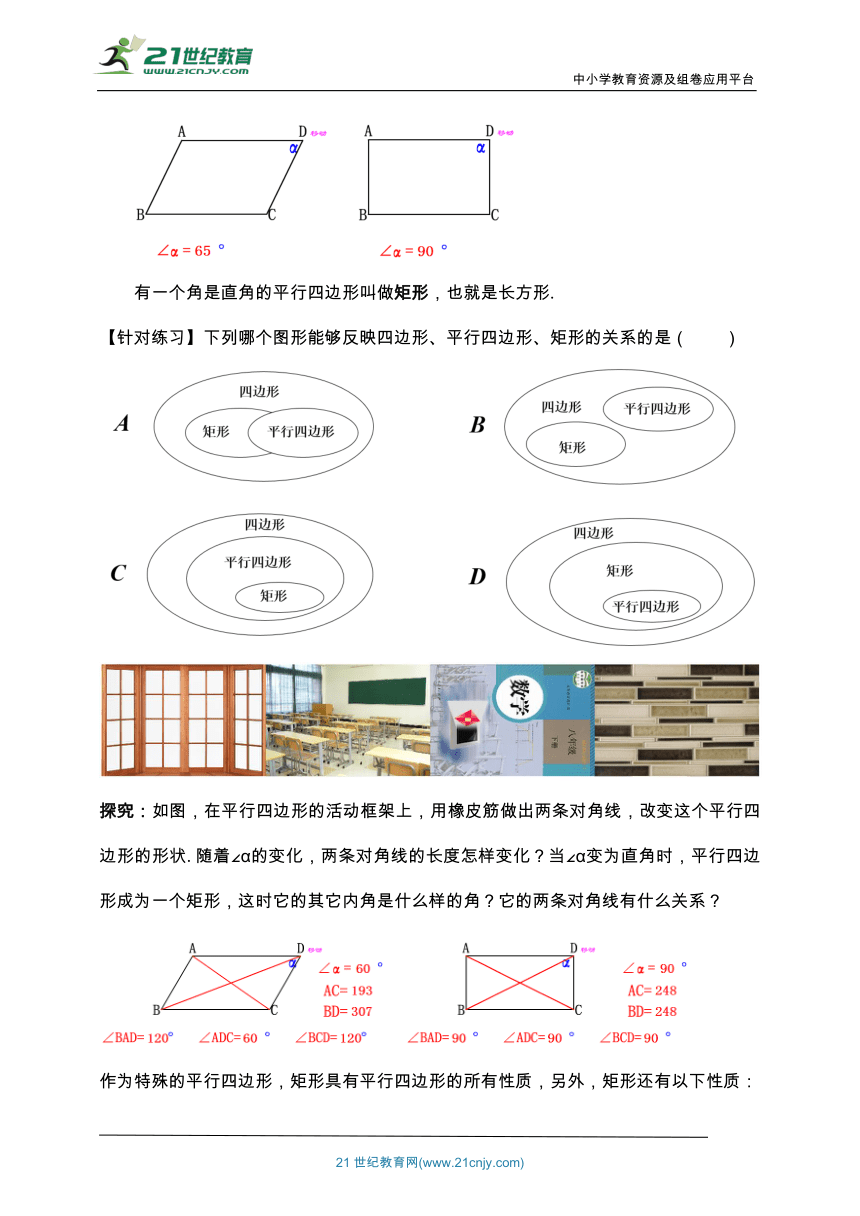
现在来看一个平行四边形,当它的一个内角由锐角变为钝角的过程中,会发生怎样的特殊情况.这时的图形是什么图形呢?
有一个角是直角的平行四边形叫做矩形,也就是长方形.
【针对练习】下列哪个图形能够反映四边形、平行四边形、矩形的关系的是( )
探究:如图,在平行四边形的活动框架上,用橡皮筋做出两条对角线,改变这个平行四边形的形状.随着∠α的变化,两条对角线的长度怎样变化?当∠α变为直角时,平行四边形成为一个矩形,这时它的其它内角是什么样的角?它的两条对角线有什么关系?
作为特殊的平行四边形,矩形具有平行四边形的所有性质,另外,矩形还有以下性质:
矩形的四个角都是直角;
矩形的对角线相等.
几何符号语言:
∵ 四边形ABCD是矩形
∴ ∠BAD=∠ABC=∠BCD=∠ADC=90°,AC=BD
你能证明矩形的这两个性质吗?
求证:矩形的对角线相等.
已知:如图,四边形ABCD是矩形.求证:AC=BD.
证明:∵ 四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°
又∵ AB=DC,BC=CB
∴ △ABC≌△DCB (SAS)
∴ AC=BD
即 矩形的对角线相等
典例解析
例1.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求矩形对角线的长.
解:∵ 四边形ABCD是矩形
∴ AC与BD相等且互相平分
∴ OA=OB
又 ∠AOB=60°
∴ △OAB是等边三角形
∴ OA=AB=4
∴ AC=BD=2OA=8
【针对练习】一个矩形的一条对角线长为8,两条对角线的一个交角为120°,求这个矩形的边长.
解:∵ 四边形ABCD是矩形
∴ AC与BD相等且互相平分
∴ OA=OB=OC= ×AC=×8=4
∵ ∠AOD=120°,∴ ∠AOB=60°
∴ △OAB是等边三角形
∴ AB=OA=4
又 ∠ABC=90°
∴ 在Rt△ABC中,BC===
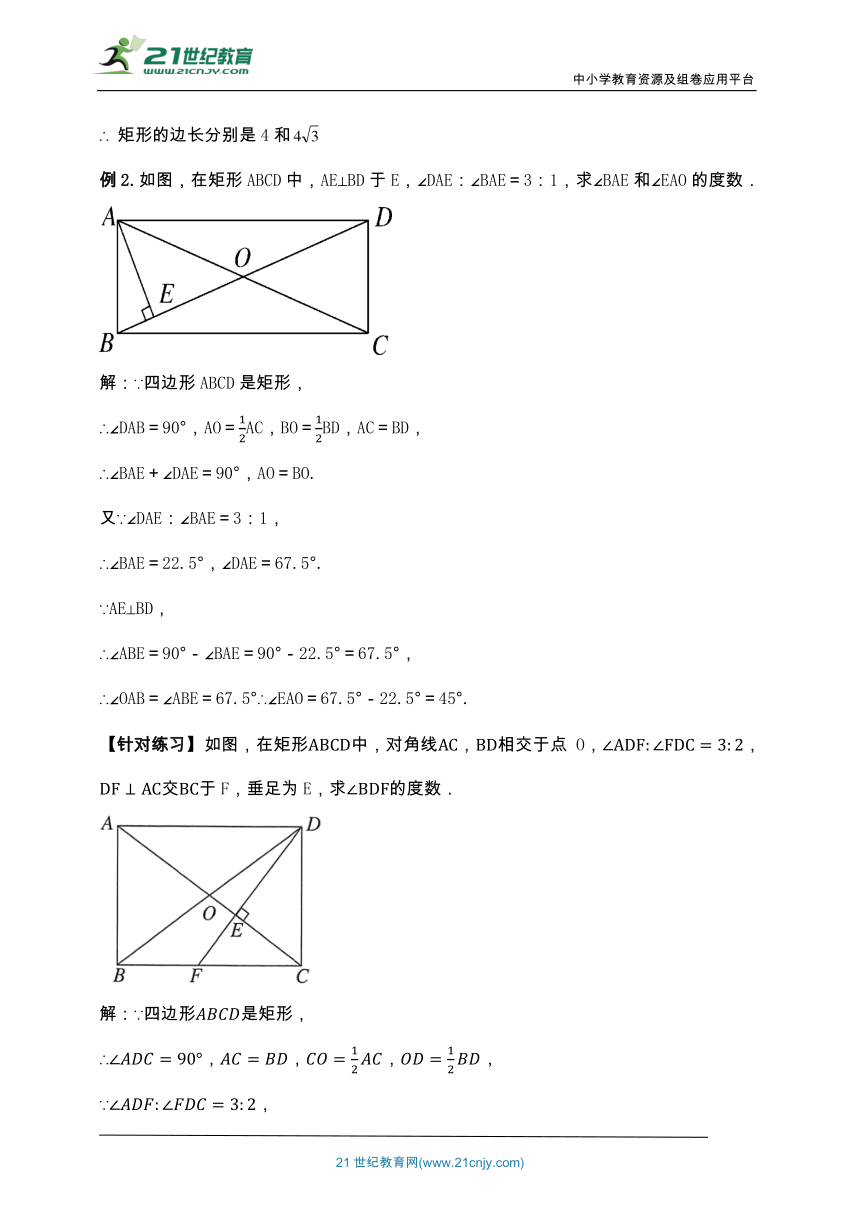
∴ 矩形的边长分别是4和
例2.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数.
解:∵四边形ABCD是矩形,
∴∠DAB=90°,AO=AC,BO=BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°∴∠EAO=67.5°-22.5°=45°.
【针对练习】如图,在矩形中,对角线相交于点O,,交于F,垂足为E,求的度数.
解:∵四边形是矩形,
∴,,,,
∵,
∴.
∵,
∴.
∴.
∵,,,
∴,
∴,
∴.
例3.如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.
证明:连接DE.
∵AD =AE,
∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE,
∴∠DFE=∠C=90°.
又∵DE=DE,
∴△DFE≌△DCE,
∴DF=DC.
例4.如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5,即DE=5.
∴S△BED=DE·AB=×5×4=10.
【针对练习】折叠矩形的一边,使点落在边的点处,若,,求:的长.
解:四边形为矩形,
,,
;
折叠矩形的一边,使点落在边的点处,
,
由勾股定理得:,
,
;
设,;
在中,由勾股定理得:,
解得:,
.
知识精讲
思考:如图,矩形ABCD的对角线AC,BD相交于点O.我们观察Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?
BO=BD=AC
直角三角形斜边上的中线等于斜边的一半.
几何符号语言:
∵ 在Rt△ABC中,OA=OC
∴ OB=AC.
典例解析
例5.如图,已知、是的两条高,M、N分别为、的中点.求证:.
解:如图,连接,,
、是的两条高,
,,
,是直角三角形,
M为的中点,
是斜边的中线,是斜边的中线,
,,
,
又 N为的中点,
.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.矩形具有一般平行四边形不具有的性质是( )
A.对角相等 B.对角线互相平分 C.对角线相等 D.对边相等
2.如图,矩形ABCD的对角线交于点O.若∠ACB=30°,AB=2,则OC的长为( )
A.2 B.3 C.2 D. 4
3.如图,矩形纸片ABCD中,AB=4, AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
4.如图,O是矩形ABCD对角线的交点,∠AOD=120°,AE平分∠BAD,则∠EAC= ______.
5.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为______.
6.如图,在Rt△ABC中,∠ACB=90°, 点D、E、F分别是边AB、BC、CA的中点.若CD+EF=8,则CD的长为______.
7.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF // BC,分别交AB、CD于E、F,连接PB、PD. 若AE=2,PF=8.则图中阴影部分的面积为_____.
8.如图,在矩形ABCD中,E是AB的中点,连接DE、CE.求证:△ADE≌ △BCE.
9.如图,在矩形ABCD中,AE⊥BD于E,对角线AC、BD相交于点O, 且BE:ED=1:3, AD=6cm.求AE的长.
10.如图,点E、F分别在矩形ABCD的边上,△DEF为等腰直角三角形,∠DEF=90°, AD+CD=10, AE=2, 求AD的长.
11.如图,在□ABCD中,E、F、G分别为AD、OB、OC的中点,且2AB=AC, 求证: EF=GF.
【参考答案】
C
A
C
15°
20
4
16
8.证明:在矩形ABCD中, AD=BC, ∠A=∠B=90°
∵E是AB的中点
∴AE=BE
∴△ADE≌△BCE (SAS)
9.解:∵四边形ABCD是矩形
∴BO=OD=BD=AC=OA,∠BAD=90°
∵BE:ED=1 :3
∴BE=OE
∵AE⊥BD
∴AB=AO=BO
∴∠ABO=60°∴∠ADE=90°-60°=30°
∴AE=AD=6=3 (cm)
10.解:∵四边形ABCD是矩形
∴CD=AB,∠A=∠B=90°
∴∠ADE+∠DEA=90°
∵△DEF为等腰直角三角形,∠DEF=90°
∴DE=EF, ∠BEF+∠DEA=90°
∴∠ADE=∠BEF
∴△ADE≌△BEF (AAS)
∴AD=BE
∵AD+CD=10,AE=2
∴AD+AB=10,即AD+AE+BE=10
∴2AD+2=10,解得,AD=4
11.证明:连接AF.
∵四边形ABCD是平行四边形.
∴AD=BC,AC=2AO
∵2AB=AC,
∴AB=AO
∵F是OB的中点,
∴AF⊥OB
在Rt△AFD中,EF为斜边AD上的中线∴EF=AD
∵F、G为OB、OC的中点
∴GF=BC
∴EF=GF
四、教学反思:
通过多媒体演示知识的探究过程,让学生在体验、实践的过程中有更直观地认识,扩大认知结构,发展能力,更好地理解平行四边形与矩形之间的从属关系和内在联系,使课堂教学真正落实到学生的发展上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
18.2.1 矩形的性质 教学设计
一、教学目标:
1.理解矩形的概念,知道矩形与平行四边形的区别与联系.
2.会证明矩形的性质,会用矩形的性质解决简单的问题.
3.掌握直角三角形斜边中线的性质,并会简单的运用.
二、教学重、难点:
重点:理解并掌握矩形的性质定理及推论,会用矩形的性质定理及推论进行推导证明.
难点:会综合运用矩形的性质定理、推论以及特殊三角形的性质进行证明与计算.
三、教学过程:
复习回顾
平行四边形的定义,及其边,角,对角线都有哪些性质呢?
定义:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行;即:AD∥BC,AB∥CD
对边相等;即:AB=DC,AD=BC
对角相等;即:∠DAB=∠BCD,∠ABC=∠CDA
对角线互相平分.即:AO=CO,BO=DO
知识精讲
现在来看一个平行四边形,当它的一个内角由锐角变为钝角的过程中,会发生怎样的特殊情况.这时的图形是什么图形呢?
有一个角是直角的平行四边形叫做矩形,也就是长方形.
【针对练习】下列哪个图形能够反映四边形、平行四边形、矩形的关系的是( )
探究:如图,在平行四边形的活动框架上,用橡皮筋做出两条对角线,改变这个平行四边形的形状.随着∠α的变化,两条对角线的长度怎样变化?当∠α变为直角时,平行四边形成为一个矩形,这时它的其它内角是什么样的角?它的两条对角线有什么关系?
作为特殊的平行四边形,矩形具有平行四边形的所有性质,另外,矩形还有以下性质:
矩形的四个角都是直角;
矩形的对角线相等.
几何符号语言:
∵ 四边形ABCD是矩形
∴ ∠BAD=∠ABC=∠BCD=∠ADC=90°,AC=BD
你能证明矩形的这两个性质吗?
求证:矩形的对角线相等.
已知:如图,四边形ABCD是矩形.求证:AC=BD.
证明:∵ 四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°
又∵ AB=DC,BC=CB
∴ △ABC≌△DCB (SAS)
∴ AC=BD
即 矩形的对角线相等
典例解析
例1.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求矩形对角线的长.
解:∵ 四边形ABCD是矩形
∴ AC与BD相等且互相平分
∴ OA=OB
又 ∠AOB=60°
∴ △OAB是等边三角形
∴ OA=AB=4
∴ AC=BD=2OA=8
【针对练习】一个矩形的一条对角线长为8,两条对角线的一个交角为120°,求这个矩形的边长.
解:∵ 四边形ABCD是矩形
∴ AC与BD相等且互相平分
∴ OA=OB=OC= ×AC=×8=4
∵ ∠AOD=120°,∴ ∠AOB=60°
∴ △OAB是等边三角形
∴ AB=OA=4
又 ∠ABC=90°
∴ 在Rt△ABC中,BC===
∴ 矩形的边长分别是4和
例2.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数.
解:∵四边形ABCD是矩形,
∴∠DAB=90°,AO=AC,BO=BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°∴∠EAO=67.5°-22.5°=45°.
【针对练习】如图,在矩形中,对角线相交于点O,,交于F,垂足为E,求的度数.
解:∵四边形是矩形,
∴,,,,
∵,
∴.
∵,
∴.
∴.
∵,,,
∴,
∴,
∴.
例3.如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.
证明:连接DE.
∵AD =AE,
∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE,
∴∠DFE=∠C=90°.
又∵DE=DE,
∴△DFE≌△DCE,
∴DF=DC.
例4.如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5,即DE=5.
∴S△BED=DE·AB=×5×4=10.
【针对练习】折叠矩形的一边,使点落在边的点处,若,,求:的长.
解:四边形为矩形,
,,
;
折叠矩形的一边,使点落在边的点处,
,
由勾股定理得:,
,
;
设,;
在中,由勾股定理得:,
解得:,
.
知识精讲
思考:如图,矩形ABCD的对角线AC,BD相交于点O.我们观察Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?
BO=BD=AC
直角三角形斜边上的中线等于斜边的一半.
几何符号语言:
∵ 在Rt△ABC中,OA=OC
∴ OB=AC.
典例解析
例5.如图,已知、是的两条高,M、N分别为、的中点.求证:.
解:如图,连接,,
、是的两条高,
,,
,是直角三角形,
M为的中点,
是斜边的中线,是斜边的中线,
,,
,
又 N为的中点,
.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.矩形具有一般平行四边形不具有的性质是( )
A.对角相等 B.对角线互相平分 C.对角线相等 D.对边相等
2.如图,矩形ABCD的对角线交于点O.若∠ACB=30°,AB=2,则OC的长为( )
A.2 B.3 C.2 D. 4
3.如图,矩形纸片ABCD中,AB=4, AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
4.如图,O是矩形ABCD对角线的交点,∠AOD=120°,AE平分∠BAD,则∠EAC= ______.
5.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为______.
6.如图,在Rt△ABC中,∠ACB=90°, 点D、E、F分别是边AB、BC、CA的中点.若CD+EF=8,则CD的长为______.
7.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF // BC,分别交AB、CD于E、F,连接PB、PD. 若AE=2,PF=8.则图中阴影部分的面积为_____.
8.如图,在矩形ABCD中,E是AB的中点,连接DE、CE.求证:△ADE≌ △BCE.
9.如图,在矩形ABCD中,AE⊥BD于E,对角线AC、BD相交于点O, 且BE:ED=1:3, AD=6cm.求AE的长.
10.如图,点E、F分别在矩形ABCD的边上,△DEF为等腰直角三角形,∠DEF=90°, AD+CD=10, AE=2, 求AD的长.
11.如图,在□ABCD中,E、F、G分别为AD、OB、OC的中点,且2AB=AC, 求证: EF=GF.
【参考答案】
C
A
C
15°
20
4
16
8.证明:在矩形ABCD中, AD=BC, ∠A=∠B=90°
∵E是AB的中点
∴AE=BE
∴△ADE≌△BCE (SAS)
9.解:∵四边形ABCD是矩形
∴BO=OD=BD=AC=OA,∠BAD=90°
∵BE:ED=1 :3
∴BE=OE
∵AE⊥BD
∴AB=AO=BO
∴∠ABO=60°∴∠ADE=90°-60°=30°
∴AE=AD=6=3 (cm)
10.解:∵四边形ABCD是矩形
∴CD=AB,∠A=∠B=90°
∴∠ADE+∠DEA=90°
∵△DEF为等腰直角三角形,∠DEF=90°
∴DE=EF, ∠BEF+∠DEA=90°
∴∠ADE=∠BEF
∴△ADE≌△BEF (AAS)
∴AD=BE
∵AD+CD=10,AE=2
∴AD+AB=10,即AD+AE+BE=10
∴2AD+2=10,解得,AD=4
11.证明:连接AF.
∵四边形ABCD是平行四边形.
∴AD=BC,AC=2AO
∵2AB=AC,
∴AB=AO
∵F是OB的中点,
∴AF⊥OB
在Rt△AFD中,EF为斜边AD上的中线∴EF=AD
∵F、G为OB、OC的中点
∴GF=BC
∴EF=GF
四、教学反思:
通过多媒体演示知识的探究过程,让学生在体验、实践的过程中有更直观地认识,扩大认知结构,发展能力,更好地理解平行四边形与矩形之间的从属关系和内在联系,使课堂教学真正落实到学生的发展上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
