18.2.2 矩形的判定(第二课时)【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 18.2.2 矩形的判定(第二课时)【2024春人教八下数学同步优质教案】 |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 21:50:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
18.2.2 矩形的判定 教学设计
一、教学目标:
1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.
2.能应用矩形的判定解决简单的证明题和计算题.
二、教学重、难点:
重点:矩形判定定理的运用.
难点:矩形判定方法的理解及应用.
三、教学过程:
复习回顾
忆一忆
1.矩形的定义:
有一个角是直角的平行四边形叫做矩形.
2.矩形的性质:
矩形的四个角都是直角;
矩形的对角线相等.
知识精讲
想一想
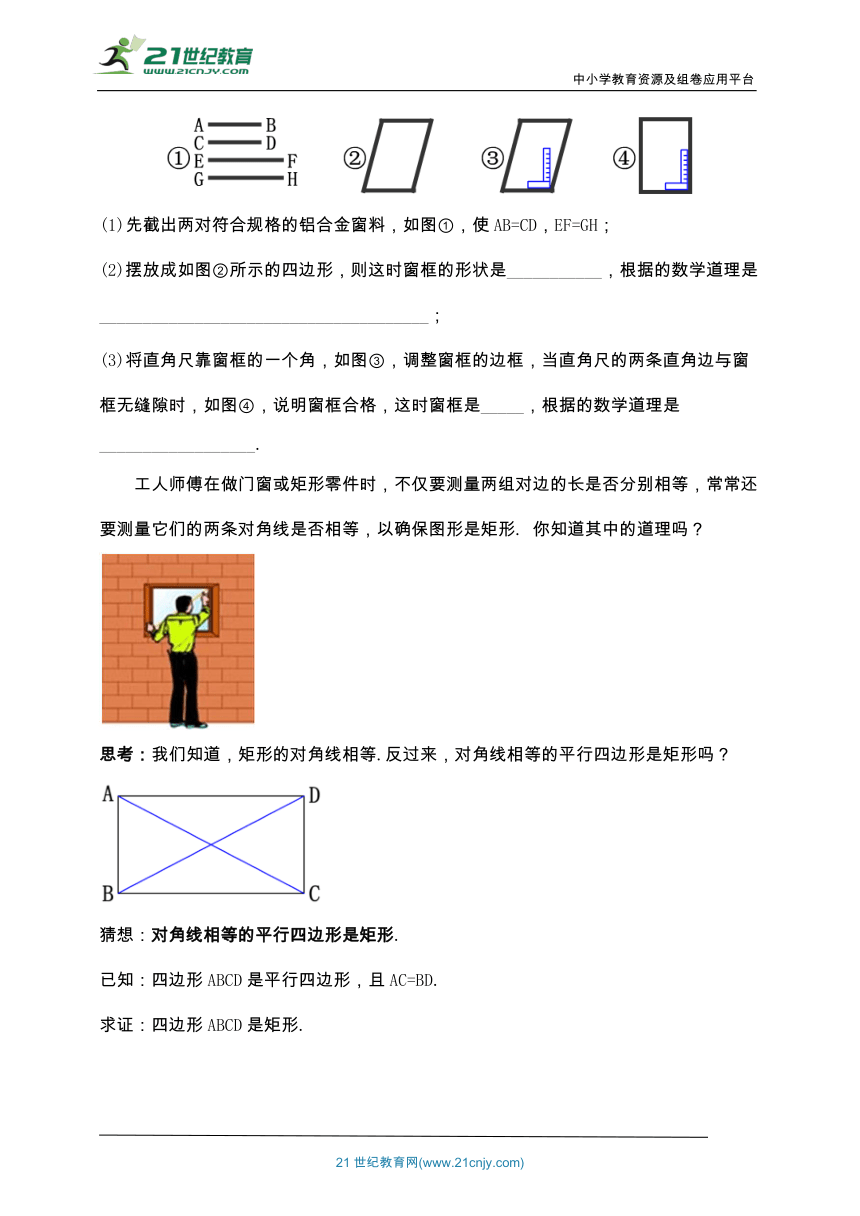
工人师傅做铝合金窗框,分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD,EF=GH;
(2)摆放成如图②所示的四边形,则这时窗框的形状是___________,根据的数学道理是______________________________________;
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图④,说明窗框合格,这时窗框是_____,根据的数学道理是__________________.
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形. 你知道其中的道理吗?
思考:我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
猜想:对角线相等的平行四边形是矩形.
已知:四边形ABCD是平行四边形,且AC=BD.
求证:四边形ABCD是矩形.
证明:∵ 四形边ABCD是平行四边形
∴ AB=DC,AB∥DC
又 AC=BD,BC=CB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
∵ AB∥DC
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=90°
∴ 四边形ABCD是矩形
矩形的判定定理1:对角线相等的平行四边形是矩形.
几何符号语言:
∵ 四边形ABCD是平行四边形,且AC=BD
∴ 四边形ABCD是矩形
想一想:对角线互相平分且相等的四边形是矩形吗?为什么?
典例解析
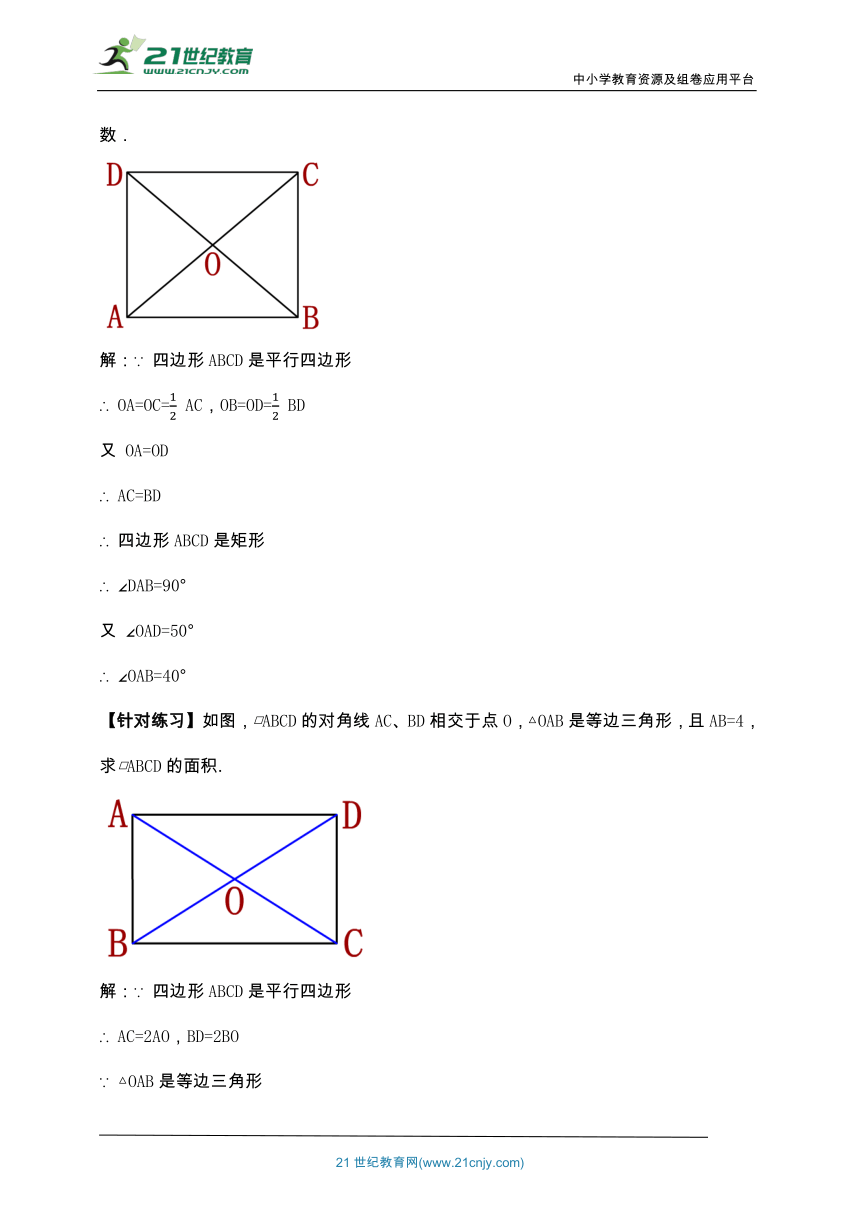
例1.如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵ 四边形ABCD是平行四边形
∴ OA=OC= AC,OB=OD= BD
又 OA=OD
∴ AC=BD
∴ 四边形ABCD是矩形
∴ ∠DAB=90°
又 ∠OAD=50°
∴ ∠OAB=40°
【针对练习】如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,求□ABCD的面积.
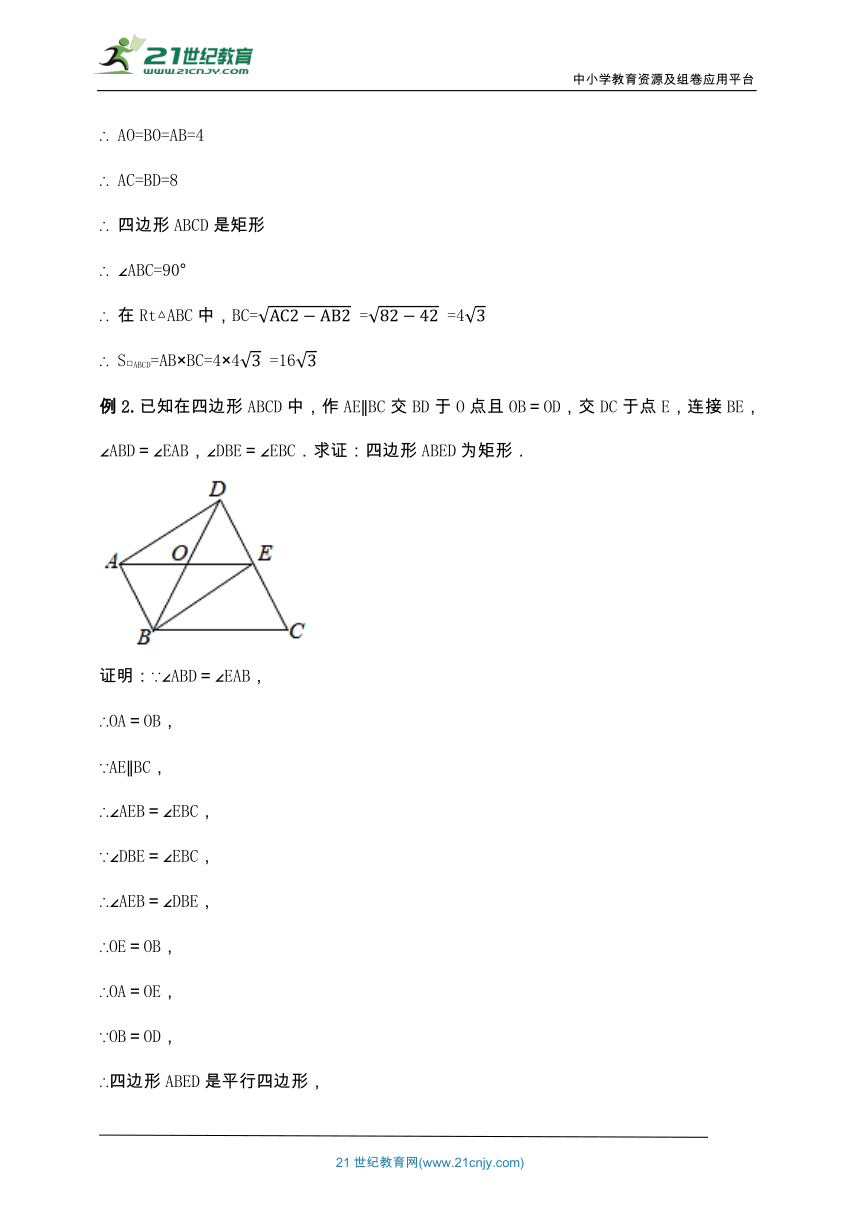
解:∵ 四边形ABCD是平行四边形
∴ AC=2AO,BD=2BO
∵ △OAB是等边三角形
∴ AO=BO=AB=4
∴ AC=BD=8
∴ 四边形ABCD是矩形
∴ ∠ABC=90°
∴ 在Rt△ABC中,BC= = =4
∴ S□ABCD=AB×BC=4×4 =16
例2.已知在四边形ABCD中,作AEBC交BD于O点且OB=OD,交DC于点E,连接BE,∠ABD=∠EAB,∠DBE=∠EBC.求证:四边形ABED为矩形.
证明:∵∠ABD=∠EAB,
∴OA=OB,
∵AEBC,
∴∠AEB=∠EBC,
∵∠DBE=∠EBC,
∴∠AEB=∠DBE,
∴OE=OB,
∴OA=OE,
∵OB=OD,
∴四边形ABED是平行四边形,
∵OA=OB,OA=OE,OB=OD,
∴OA=OE=OB=OD,
∴AE=BD,
∴平行四边形ABED为矩形.
【针对练习】如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO,
∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
知识精讲
思考:前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
几何符号语言:
∵ ∠A=∠B=∠C=90°
∴ 四边形ABCD是矩形
典例解析
例3.如图,平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形EFGH是矩形.
证明:∵四边形ABCD是平行四边形
∴AB // CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
∴∠GBC+∠GCB=(∠ABC+∠BCD) =90°
即∠G=90°
同理∠E=90°,∠AFB=90°
∴∠GFE=90°
∴四边形EFGH是矩形
【针对练习】已知:如图,P,B,C在同一条直线上,,分别是与的平分线,,E,D为垂足.求证:四边形是矩形.
证明:∵,分别是与的平分线,
,
,
即,
,,
∴四边形是矩形.
例4.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=∠CAM,
∴∠DAE=∠DAC+∠CAE= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
例5.在矩形ABCD中,AB=4,BC=3.若点P是CD上任意一点,如图①,PE⊥BD于点E,PF⊥AC于点F.
(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.
(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系
(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.
(1)解:连接,如图,
设点到的距离为.
在中,,
由,得
.
四边形是矩形,
,
由,得,
,
化简得.
(2)解:,理由见解析,
连接,如下图:
设点到的距离为,
由(1)得,
,
,
,
(3)解:,理由如下:
连接、,如图.
由
,
,
化简得,
即.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.在数学活动课.上,老师让同学们判断一个四边形门框是否为矩形,下面是某合作小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B. 测量两组对边是否分别相等
C.测量一组对角是否为直角 D.测量其中三个角是否为直角
2.已知平行四边形ABCD中, 下列条件:①AB=BC; ②AC=BD;③AC⊥BD;④AC平分∠BAD.其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
3.如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.若AD=4,∠ABD=30°,则AB的长为( )
A.4 B.2 C.8 D. 8
4.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°, BC=2,AF=BF, 则四边形BCDE的面积是( )
A.2 B.4 C.4 D.2
5.如图,是四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,使AB固定,转动AD,当∠DAB=_____时,□ABCD的面积最大,此时□ ABCD是_____形,面积为______cm2.
6.如图,在矩形ABCD中,M为AD边的中点,P为BC上一点,PE⊥MC,PF⊥ MB, 当AB、BC满足条件___________时,四边形PEMF为矩形.
7.如图,在矩形ABCD中AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF // BC交AB于点F,连接EF,则EF的最小值为______.
8.已知:如图,在四边形中,,点M,N,P,Q分别是的中点.求证:四边形是矩形.
9.如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(1)若AB=4,BC=3,求AE的长.
(2)连接DF,若点D,F,E在同一条直线上,且DF=2,求AE的长.
10.如图,在四边形中,,,,,,动点从点开始沿边向点以的速度运动,动点从点开始沿边向点以的速度运动,动点,分别从点,同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为秒.
(1)当为何值时,四边形为矩形?
(2)当为何值时,四边形为平行四边形?
【参考答案】
D
B
A
A
90°,矩,48
AB=BC
8.证明:设与交于点O,与交于点F,与交于点E,
∵,,
∴点A与点C都在的垂直平分线上,
∴是的垂直平分线,即,
∴,
∵点M,N,N,P,Q分别是,,,的中点,
∴,,
∴四边形是平行四边形,
又,
∴四边形是矩形,
∴,
同理:,
∴四边形是矩形.
9.(1)解:如图,矩形纸片ABCD中,
∵AB=4,BC=3,
故由勾股定理可得AC=5.
由折叠知:FC=BC=3,∠EFC=∠B=90°,BE=FE.
∴.
设AE=x,则.
在Rt△AFE中,,
解得:.
∴.
(2)如图,矩形纸片ABCD中,
∵,∴∠DCE=∠BEC,
由折叠知:∠BEC=∠FEC,
∴∠DCE=∠FEC,
∴DC=DE.
又∵点D,F,E在同一条直线上,∠EFC=∠B,
∴∠DFC=90°,
∴∠DFC=∠DAE=90°,
而CF=CB=DA,
∴,∴AE=DF=2.
10.(1)解:设运动时间为秒,
,,,,
如图1,
,
当时,四边形是平行四边形,
,
四边形是矩形,
即,
解得:,
时,四边形是矩形;
(2)解:如图2,
,
当时,四边形是平行四边形.
此时有,
解得.
当时,四边形是平行四边形.
四、教学反思:
在本节课的教学中,不仅要让学生掌握矩形判定的几种方法,更要注重学生在学习的过程中是否真正掌握了探究问题的基本思路和方法. 教师在例题练习的教学中,若能适当地引导学生多做一些变式练习,类比、迁移地思考、做题,就能进一步拓展学生的思维,提高课堂教学的效率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
18.2.2 矩形的判定 教学设计
一、教学目标:
1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.
2.能应用矩形的判定解决简单的证明题和计算题.
二、教学重、难点:
重点:矩形判定定理的运用.
难点:矩形判定方法的理解及应用.
三、教学过程:
复习回顾
忆一忆
1.矩形的定义:
有一个角是直角的平行四边形叫做矩形.
2.矩形的性质:
矩形的四个角都是直角;
矩形的对角线相等.
知识精讲
想一想
工人师傅做铝合金窗框,分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD,EF=GH;
(2)摆放成如图②所示的四边形,则这时窗框的形状是___________,根据的数学道理是______________________________________;
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图④,说明窗框合格,这时窗框是_____,根据的数学道理是__________________.
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形. 你知道其中的道理吗?
思考:我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
猜想:对角线相等的平行四边形是矩形.
已知:四边形ABCD是平行四边形,且AC=BD.
求证:四边形ABCD是矩形.
证明:∵ 四形边ABCD是平行四边形
∴ AB=DC,AB∥DC
又 AC=BD,BC=CB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
∵ AB∥DC
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=90°
∴ 四边形ABCD是矩形
矩形的判定定理1:对角线相等的平行四边形是矩形.
几何符号语言:
∵ 四边形ABCD是平行四边形,且AC=BD
∴ 四边形ABCD是矩形
想一想:对角线互相平分且相等的四边形是矩形吗?为什么?
典例解析
例1.如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵ 四边形ABCD是平行四边形
∴ OA=OC= AC,OB=OD= BD
又 OA=OD
∴ AC=BD
∴ 四边形ABCD是矩形
∴ ∠DAB=90°
又 ∠OAD=50°
∴ ∠OAB=40°
【针对练习】如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,求□ABCD的面积.
解:∵ 四边形ABCD是平行四边形
∴ AC=2AO,BD=2BO
∵ △OAB是等边三角形
∴ AO=BO=AB=4
∴ AC=BD=8
∴ 四边形ABCD是矩形
∴ ∠ABC=90°
∴ 在Rt△ABC中,BC= = =4
∴ S□ABCD=AB×BC=4×4 =16
例2.已知在四边形ABCD中,作AEBC交BD于O点且OB=OD,交DC于点E,连接BE,∠ABD=∠EAB,∠DBE=∠EBC.求证:四边形ABED为矩形.
证明:∵∠ABD=∠EAB,
∴OA=OB,
∵AEBC,
∴∠AEB=∠EBC,
∵∠DBE=∠EBC,
∴∠AEB=∠DBE,
∴OE=OB,
∴OA=OE,
∵OB=OD,
∴四边形ABED是平行四边形,
∵OA=OB,OA=OE,OB=OD,
∴OA=OE=OB=OD,
∴AE=BD,
∴平行四边形ABED为矩形.
【针对练习】如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO,
∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
知识精讲
思考:前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
几何符号语言:
∵ ∠A=∠B=∠C=90°
∴ 四边形ABCD是矩形
典例解析
例3.如图,平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形EFGH是矩形.
证明:∵四边形ABCD是平行四边形
∴AB // CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
∴∠GBC+∠GCB=(∠ABC+∠BCD) =90°
即∠G=90°
同理∠E=90°,∠AFB=90°
∴∠GFE=90°
∴四边形EFGH是矩形
【针对练习】已知:如图,P,B,C在同一条直线上,,分别是与的平分线,,E,D为垂足.求证:四边形是矩形.
证明:∵,分别是与的平分线,
,
,
即,
,,
∴四边形是矩形.
例4.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=∠CAM,
∴∠DAE=∠DAC+∠CAE= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
例5.在矩形ABCD中,AB=4,BC=3.若点P是CD上任意一点,如图①,PE⊥BD于点E,PF⊥AC于点F.
(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.
(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系
(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.
(1)解:连接,如图,
设点到的距离为.
在中,,
由,得
.
四边形是矩形,
,
由,得,
,
化简得.
(2)解:,理由见解析,
连接,如下图:
设点到的距离为,
由(1)得,
,
,
,
(3)解:,理由如下:
连接、,如图.
由
,
,
化简得,
即.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.在数学活动课.上,老师让同学们判断一个四边形门框是否为矩形,下面是某合作小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B. 测量两组对边是否分别相等
C.测量一组对角是否为直角 D.测量其中三个角是否为直角
2.已知平行四边形ABCD中, 下列条件:①AB=BC; ②AC=BD;③AC⊥BD;④AC平分∠BAD.其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
3.如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.若AD=4,∠ABD=30°,则AB的长为( )
A.4 B.2 C.8 D. 8
4.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°, BC=2,AF=BF, 则四边形BCDE的面积是( )
A.2 B.4 C.4 D.2
5.如图,是四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,使AB固定,转动AD,当∠DAB=_____时,□ABCD的面积最大,此时□ ABCD是_____形,面积为______cm2.
6.如图,在矩形ABCD中,M为AD边的中点,P为BC上一点,PE⊥MC,PF⊥ MB, 当AB、BC满足条件___________时,四边形PEMF为矩形.
7.如图,在矩形ABCD中AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF // BC交AB于点F,连接EF,则EF的最小值为______.
8.已知:如图,在四边形中,,点M,N,P,Q分别是的中点.求证:四边形是矩形.
9.如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(1)若AB=4,BC=3,求AE的长.
(2)连接DF,若点D,F,E在同一条直线上,且DF=2,求AE的长.
10.如图,在四边形中,,,,,,动点从点开始沿边向点以的速度运动,动点从点开始沿边向点以的速度运动,动点,分别从点,同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为秒.
(1)当为何值时,四边形为矩形?
(2)当为何值时,四边形为平行四边形?
【参考答案】
D
B
A
A
90°,矩,48
AB=BC
8.证明:设与交于点O,与交于点F,与交于点E,
∵,,
∴点A与点C都在的垂直平分线上,
∴是的垂直平分线,即,
∴,
∵点M,N,N,P,Q分别是,,,的中点,
∴,,
∴四边形是平行四边形,
又,
∴四边形是矩形,
∴,
同理:,
∴四边形是矩形.
9.(1)解:如图,矩形纸片ABCD中,
∵AB=4,BC=3,
故由勾股定理可得AC=5.
由折叠知:FC=BC=3,∠EFC=∠B=90°,BE=FE.
∴.
设AE=x,则.
在Rt△AFE中,,
解得:.
∴.
(2)如图,矩形纸片ABCD中,
∵,∴∠DCE=∠BEC,
由折叠知:∠BEC=∠FEC,
∴∠DCE=∠FEC,
∴DC=DE.
又∵点D,F,E在同一条直线上,∠EFC=∠B,
∴∠DFC=90°,
∴∠DFC=∠DAE=90°,
而CF=CB=DA,
∴,∴AE=DF=2.
10.(1)解:设运动时间为秒,
,,,,
如图1,
,
当时,四边形是平行四边形,
,
四边形是矩形,
即,
解得:,
时,四边形是矩形;
(2)解:如图2,
,
当时,四边形是平行四边形.
此时有,
解得.
当时,四边形是平行四边形.
四、教学反思:
在本节课的教学中,不仅要让学生掌握矩形判定的几种方法,更要注重学生在学习的过程中是否真正掌握了探究问题的基本思路和方法. 教师在例题练习的教学中,若能适当地引导学生多做一些变式练习,类比、迁移地思考、做题,就能进一步拓展学生的思维,提高课堂教学的效率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
