18.2.3 菱形的性质(第一课时)【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 18.2.3 菱形的性质(第一课时)【2024春人教八下数学同步优质教案】 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 16:01:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
18.2.3 菱形的性质 教学设计
一、教学目标:
1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.
3.应用菱形的性质定理解决相关计算或证明问题.
二、教学重、难点:
重点:掌握菱形的定义和性质及菱形面积的求法.
难点:灵活运用菱形的性质解决问题.
三、教学过程:
复习回顾
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
知识精讲
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?
有一组邻边相等的平行四边形叫做菱形.
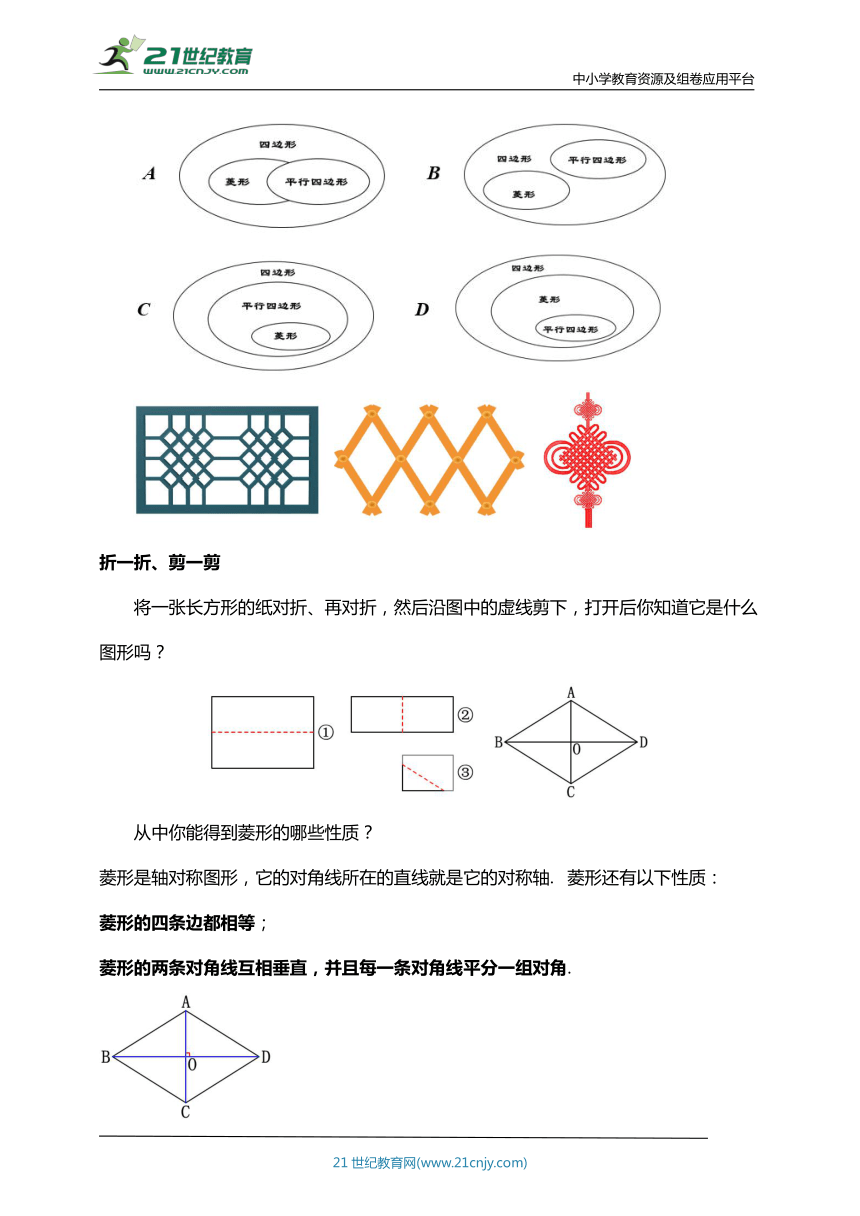
【针对练习】下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
折一折、剪一剪
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开后你知道它是什么图形吗?
从中你能得到菱形的哪些性质?
菱形是轴对称图形,它的对角线所在的直线就是它的对称轴. 菱形还有以下性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
几何符号语言:
∵ 四边形ABCD是菱形
∴ AB=BC=CD=AD,AC⊥BD
AC平分∠BAD,AC平分∠BCD
BD平分∠ABC,BD平分∠ADC
求证:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:如图,菱形ABCD的对角线相交于O点.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
证明:∵ 四边形ABCD是菱形
∴ AB=AD,OB=OD
∴ AC⊥BD,AC平分∠BAD (等腰三角形的三线合一)
同理,AC平分∠BCD,BD平分∠ABC和∠ADC.
如图,比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成四个全等的三角形,而平行四边形通常只被分成两对全等的三角形.
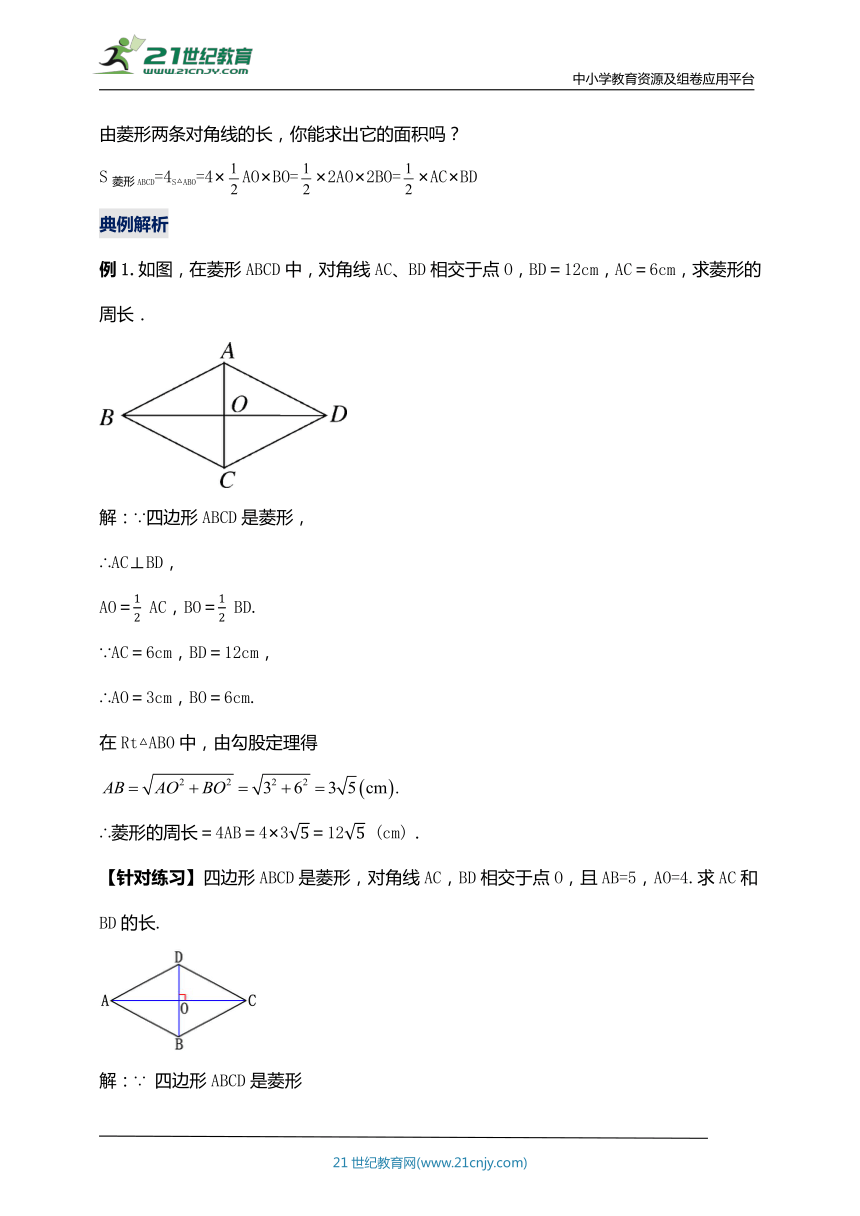
由菱形两条对角线的长,你能求出它的面积吗?
S菱形ABCD=4S△ABO=4×AO×BO=×2AO×2BO=×AC×BD
典例解析
例1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= AC,BO= BD.
∵AC=6cm,BD=12cm,
∴AO=3cm,BO=6cm.
在Rt△ABO中,由勾股定理得
∴菱形的周长=4AB=4×3=12 (cm).
【针对练习】四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
解:∵ 四边形ABCD是菱形
∴ AC⊥BD,BD=2OB,AC=2AO=8
在Rt△AOB中,OB===3
∴ BD=6
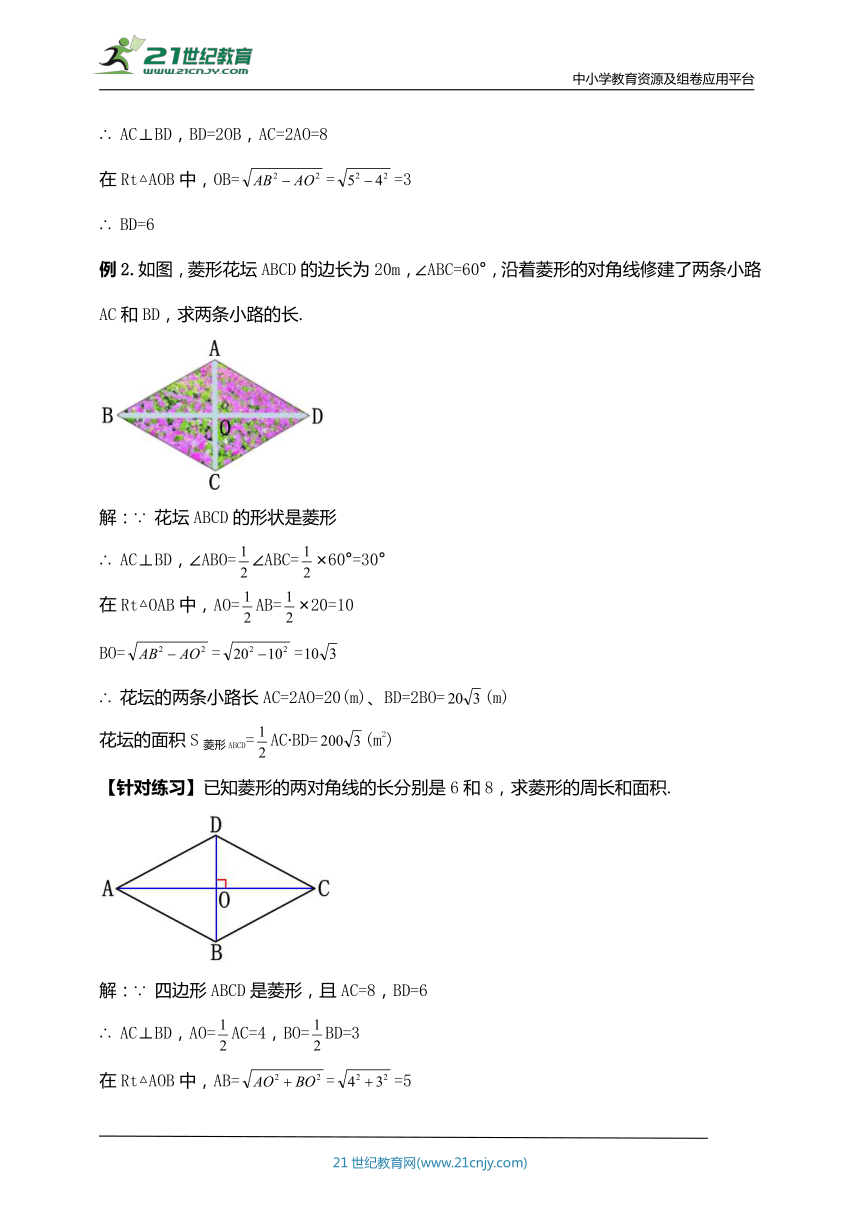
例2.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长.
解:∵ 花坛ABCD的形状是菱形
∴ AC⊥BD,∠ABO=∠ABC=×60°=30°
在Rt△OAB中,AO=AB=×20=10
BO===
∴ 花坛的两条小路长AC=2AO=20(m)、BD=2BO=(m)
花坛的面积S菱形ABCD=AC·BD=(m2)
【针对练习】已知菱形的两对角线的长分别是6和8,求菱形的周长和面积.
解:∵ 四边形ABCD是菱形,且AC=8,BD=6
∴ AC⊥BD,AO=AC=4,BO=BD=3
在Rt△AOB中,AB===5
∴ C菱形ABCD=4×5=20
S菱形ABCD=×6×8=24
例3.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA ,
∴AO=BE .
【针对练习】如图,在菱形ABCD中,CE⊥AB于E, CF⊥AD于F.求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形
∴AC平分∠BAD,即∠EAC=∠FAC
∵CE⊥AB,CF⊥AD
∴∠AEC=∠AFC=90°
又AC=AC
∴△ACE≌△ACF (AAS)
∴AE=AF
例4.如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB=OA·OB=×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵AB= = =13
∴ C菱形ABCD=4×5=20
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h=.
【点睛】菱形的面积计算有如下方法:(1)一边长与两对边的距离(即菱形的高)的积;(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);(3)两条对角线长度乘积的一半.
【针对练习】如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°.
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=×180°=60°,
∴∠ABO=×∠ABC=30°,△ABC是等边三角形.
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=AB=1cm,AC=AB=2cm,
OB= = cm
∴BD=2OB=2cm;
(2)S菱形ABCD=AC BD=×2×2=2 (cm2).
【点睛】菱形中的相关计算通常转化为直角三角形或等腰三角形,当菱形中有一个角是60°时,菱形被分为以60°为顶角的两个等边三角形.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.菱形具有而一-般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等
2.如图,在菱形ABCD中, AB=5, ∠BCD=120°,则对角线AC的长是( )
A. 20 B.15 C.10 D.5
3.菱形两条对角线分别为6和4,则菱形的周长是( )
A.24 B.16 C.4 D.2
4.如图,在菱形ABCD中,AB=5,AC=6, 过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
5.如图,P为线段AB上的一个点,分别以AP, PB为边在AB的同侧作菱形APCD和菱形PBFE,点P, C, E在一条直线上.若∠DAP=60°, AP2+3PB2=1,M,N分别是对角线AC,BE的中点,则MN的长为( )
A. B. C.1 D.4
6.菱形的周长是8,则菱形的一边长是______.
7.菱形的面积为24,一对角线长为6,则另一对角线长为_____,边长为_____.
8.如图,一活动菱形衣架中,菱形的边均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1=______度.
9.如图,菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB 上,且BE=BO,则∠EOA=_____度.
10.如图,在边长为2的菱形ABCD中,∠ABC=120°,E,F分别为AD,CD上的动点,且AE+CF=2, 则线段EF长的最小值是______.
11.如图,在菱形ABCD中,E、F分别是BC、CD上的点,且BE=DF.求证:∠AEF=∠AFE.
12.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.
【参考答案】
C
D
C
D
A
2
8,5
120
25
11.证明:∵四边形ABCD是菱形
∴AB=AD,∠B=∠D
∵BE=DF
∴△ABE≌△ADF(SAS)
∴AE=AF
∴∠AEF=∠AFE
12.证明:∵四边形ABCD是菱形
∴AC⊥BD,AB // CD,OB=OD
∴∠DCO+∠CDO=90°,∠CDO=∠HBO
∵DH⊥AB
∴OH是Rt△BDH斜边BD上的中线
∴OH=OB
∴∠OHB=∠HBO
∴∠OHB=∠CDO
∵∠DHO+∠OHB=90°
∴∠DHO=∠DCO
四、教学反思:
通过剪纸活动让学生主动探索菱形的性质,大多数学生能全部得到结论,少数需要教师加以引导. 但是学生得到的结论,有一些是他们的猜想,是否正确还需要证明,因此问题就上升到证明这个环节. 在整个新知生成过程中,探究活动起了重要的作用. 课堂中学生始终处于观察、比较、概括、总结和积极思维状态,切身感受到自己是学习的主人. 为学生今后获取知识、探索发现和创造打下了良好的基础,更增强了敢于实践,勇于探索,不断创新和努力学习数学知识的信心和勇气.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
18.2.3 菱形的性质 教学设计
一、教学目标:
1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.
3.应用菱形的性质定理解决相关计算或证明问题.
二、教学重、难点:
重点:掌握菱形的定义和性质及菱形面积的求法.
难点:灵活运用菱形的性质解决问题.
三、教学过程:
复习回顾
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
知识精讲
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?
有一组邻边相等的平行四边形叫做菱形.
【针对练习】下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
折一折、剪一剪
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开后你知道它是什么图形吗?
从中你能得到菱形的哪些性质?
菱形是轴对称图形,它的对角线所在的直线就是它的对称轴. 菱形还有以下性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
几何符号语言:
∵ 四边形ABCD是菱形
∴ AB=BC=CD=AD,AC⊥BD
AC平分∠BAD,AC平分∠BCD
BD平分∠ABC,BD平分∠ADC
求证:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:如图,菱形ABCD的对角线相交于O点.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
证明:∵ 四边形ABCD是菱形
∴ AB=AD,OB=OD
∴ AC⊥BD,AC平分∠BAD (等腰三角形的三线合一)
同理,AC平分∠BCD,BD平分∠ABC和∠ADC.
如图,比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成四个全等的三角形,而平行四边形通常只被分成两对全等的三角形.
由菱形两条对角线的长,你能求出它的面积吗?
S菱形ABCD=4S△ABO=4×AO×BO=×2AO×2BO=×AC×BD
典例解析
例1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= AC,BO= BD.
∵AC=6cm,BD=12cm,
∴AO=3cm,BO=6cm.
在Rt△ABO中,由勾股定理得
∴菱形的周长=4AB=4×3=12 (cm).
【针对练习】四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
解:∵ 四边形ABCD是菱形
∴ AC⊥BD,BD=2OB,AC=2AO=8
在Rt△AOB中,OB===3
∴ BD=6
例2.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长.
解:∵ 花坛ABCD的形状是菱形
∴ AC⊥BD,∠ABO=∠ABC=×60°=30°
在Rt△OAB中,AO=AB=×20=10
BO===
∴ 花坛的两条小路长AC=2AO=20(m)、BD=2BO=(m)
花坛的面积S菱形ABCD=AC·BD=(m2)
【针对练习】已知菱形的两对角线的长分别是6和8,求菱形的周长和面积.
解:∵ 四边形ABCD是菱形,且AC=8,BD=6
∴ AC⊥BD,AO=AC=4,BO=BD=3
在Rt△AOB中,AB===5
∴ C菱形ABCD=4×5=20
S菱形ABCD=×6×8=24
例3.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA ,
∴AO=BE .
【针对练习】如图,在菱形ABCD中,CE⊥AB于E, CF⊥AD于F.求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形
∴AC平分∠BAD,即∠EAC=∠FAC
∵CE⊥AB,CF⊥AD
∴∠AEC=∠AFC=90°
又AC=AC
∴△ACE≌△ACF (AAS)
∴AE=AF
例4.如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB=OA·OB=×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵AB= = =13
∴ C菱形ABCD=4×5=20
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h=.
【点睛】菱形的面积计算有如下方法:(1)一边长与两对边的距离(即菱形的高)的积;(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);(3)两条对角线长度乘积的一半.
【针对练习】如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180°.
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=×180°=60°,
∴∠ABO=×∠ABC=30°,△ABC是等边三角形.
∵菱形ABCD的周长是8cm.
∴AB=2cm,
∴OA=AB=1cm,AC=AB=2cm,
OB= = cm
∴BD=2OB=2cm;
(2)S菱形ABCD=AC BD=×2×2=2 (cm2).
【点睛】菱形中的相关计算通常转化为直角三角形或等腰三角形,当菱形中有一个角是60°时,菱形被分为以60°为顶角的两个等边三角形.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.菱形具有而一-般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等
2.如图,在菱形ABCD中, AB=5, ∠BCD=120°,则对角线AC的长是( )
A. 20 B.15 C.10 D.5
3.菱形两条对角线分别为6和4,则菱形的周长是( )
A.24 B.16 C.4 D.2
4.如图,在菱形ABCD中,AB=5,AC=6, 过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A. B. C.4 D.
5.如图,P为线段AB上的一个点,分别以AP, PB为边在AB的同侧作菱形APCD和菱形PBFE,点P, C, E在一条直线上.若∠DAP=60°, AP2+3PB2=1,M,N分别是对角线AC,BE的中点,则MN的长为( )
A. B. C.1 D.4
6.菱形的周长是8,则菱形的一边长是______.
7.菱形的面积为24,一对角线长为6,则另一对角线长为_____,边长为_____.
8.如图,一活动菱形衣架中,菱形的边均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1=______度.
9.如图,菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB 上,且BE=BO,则∠EOA=_____度.
10.如图,在边长为2的菱形ABCD中,∠ABC=120°,E,F分别为AD,CD上的动点,且AE+CF=2, 则线段EF长的最小值是______.
11.如图,在菱形ABCD中,E、F分别是BC、CD上的点,且BE=DF.求证:∠AEF=∠AFE.
12.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.
【参考答案】
C
D
C
D
A
2
8,5
120
25
11.证明:∵四边形ABCD是菱形
∴AB=AD,∠B=∠D
∵BE=DF
∴△ABE≌△ADF(SAS)
∴AE=AF
∴∠AEF=∠AFE
12.证明:∵四边形ABCD是菱形
∴AC⊥BD,AB // CD,OB=OD
∴∠DCO+∠CDO=90°,∠CDO=∠HBO
∵DH⊥AB
∴OH是Rt△BDH斜边BD上的中线
∴OH=OB
∴∠OHB=∠HBO
∴∠OHB=∠CDO
∵∠DHO+∠OHB=90°
∴∠DHO=∠DCO
四、教学反思:
通过剪纸活动让学生主动探索菱形的性质,大多数学生能全部得到结论,少数需要教师加以引导. 但是学生得到的结论,有一些是他们的猜想,是否正确还需要证明,因此问题就上升到证明这个环节. 在整个新知生成过程中,探究活动起了重要的作用. 课堂中学生始终处于观察、比较、概括、总结和积极思维状态,切身感受到自己是学习的主人. 为学生今后获取知识、探索发现和创造打下了良好的基础,更增强了敢于实践,勇于探索,不断创新和努力学习数学知识的信心和勇气.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
