18.2.5 正方形【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 18.2.5 正方形【2024春人教八下数学同步优质教案】 |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 16:06:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
18.2.5 正方形 教学设计
一、教学目标:
1.理解正方形的概念;
2.探索正方形的性质与判定,并了解平行四边形、矩形、菱形之间的联系和区别;
3.会应用正方形的性质与判定解决相关证明及计算问题.
二、教学重、难点:
重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
三、教学过程:
情境引入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
知识精讲
正方形的四个角都是_____,四条边都_____.因此,正方形既是______,又是______,它既有______的性质,又有______的性质.
正方形是轴对称图形吗?它的对称轴是什么?
正方形有哪些性质?
实验探究
实验一:利用手中矩形纸片用最快的方法剪出一个正方形.
实验二:如何将一个活动的菱形框变成一个正方形?
思考
1.如果四边形ABCD已经是一个矩形,那么再加上什么条件就可以变为正方形?
2.如果四边形ABCD已经是一个菱形,那么再加上什么条件就可以变为正方形?
3.如果四边形ABCD是一般的平行四边形,那么再加上什么条件就可以变为正方形?
有一组邻边相等的矩形是正方形:有一个角是直角的菱形是正方形;有一组邻边相等且有一个角是直角的平行四边形是正方形.
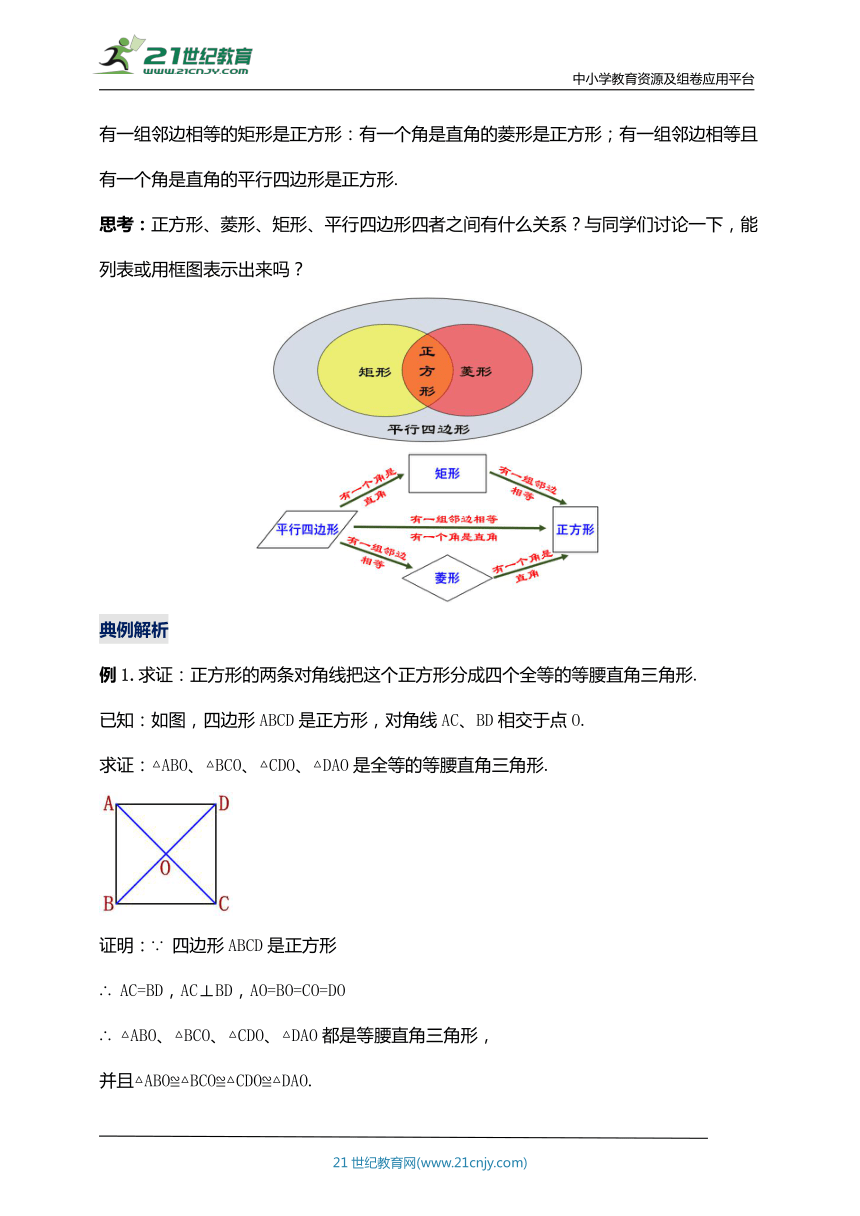
思考:正方形、菱形、矩形、平行四边形四者之间有什么关系?与同学们讨论一下,能列表或用框图表示出来吗?
典例解析
例1.求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵ 四边形ABCD是正方形
∴ AC=BD,AC⊥BD,AO=BO=CO=DO
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
并且△ABO≌△BCO≌△CDO≌△DAO.
例2.如图,在正方形ABCD中,ΔBEC是等边三角形.求证:∠EAD=∠EDA=15°.
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
【针对练习】四边形ABCD是正方形,以正方形ABCD的一边作等边△ADE,求∠BEC的大小.
解:当等边△ADE在正方形ABCD外部时,如图①,
AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
【点睛】因为等边△ADE与正方形ABCD有一条公共边,所以边相等.本题分两种情况:等边△ADE在正方形的外部或在正方形的内部.
例3.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
解:连接PC,AC.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴AP=PC.
又∵PE⊥BC ,PF⊥DC,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=EF.
【点睛】在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
【针对练习】如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
∴∠DCF=180°-∠BCE=90°.
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
延长BE交DE于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°,
∴∠CBE+∠F=90° ,
∴∠BMF=90°.
∴BE⊥DF.
例4.在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,∠A=∠B=∠C=∠D,AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)=180°-(∠AEN+∠ANE)=180°-90°=90°.
∴四边形EFMN是正方形 .
【针对练习】如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
例5.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB ,∠DAE=∠BAF ,AE=AF ,
∴△ADE≌△ABF(SAS),∴BF=DE;
(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE=AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴得平行四边形AFBE,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.四个角都是直角
C.四条边都相等 D.对角线互相垂直
2.已知四边形ABCD中, ∠A=∠B=∠C=90°, 如果再添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B. AB=CD C. AD=BC D. BC=CD
3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时, 它是矩形 D.当AC=BD时,它是正方形
4.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为( )
A.2 B.4-π C.π D.π-1
5.正方形的一条边长是3,那么它的对角线长是_______.
6.如图,正方形ABCD的两条对角线AC,BD交于点O,点E在BD上,且BE=CD, 则∠BEC的度数为_________.
7.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.
8.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE//CA,DF//BA.
(1)四边形AEDF是______________;
(2)如果∠BAC=90°,那么四边形AEDF是_________;
(3)如果AD平分∠BAC,那么四边形AEDF是_________;
(4)如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是__________.
9.如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连接AF、BD,延长BD交AF于H.求证:BH⊥AF.
10.如图,在正方形ABCD中,Q在CD上,且DQ=CQ,P在BC上,AP=CD+CP,求证: AQ平分∠DAP.
11.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)证明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=BC,证明平行四边形EGFH是正方形.
【参考答案】
B
D
D
B
3
67.5°
2
(1)平行四边形;(2)矩形;(3)菱形;(4)正方形
9.证明:∵四边形AEDC和BCFG是正方形∴AC=DC,CF=CB, ∠ACF=∠BCF=90°
∴△ACF≌△DCB (SAS)
∴∠AFC=∠DBC
又∵∠AFC+∠CAF=90°
∴∠DBC+ ∠CAF=90°
∴∠AHB=90° 即 BH⊥AF
10.证明:延长AQ交BC延长线与E.
∵四边形ABCD是正方形
∴AD=CD,AD// BC
∵∠D=∠QCE,∠DAQ=∠E
又∵DQ=CQ
∴△ADQ≌△ECQ (AAS)
∴AD=CE
∴CD=CE
∴AP=CD+CP=CE+CP=EP
∴∠PAQ=∠E
∴∠PAQ=∠DAQ,即AQ平分∠DAP
11.证明:(1)∵G,F,H分别是BE,BC,CE的中点∴GF//CE,FH//BE
∴GF//EH,FH//GE
∴四边形EGFH是平行四边形
证明:(2)连接EF.
∵BF=CF,EF⊥BC
∴BE=CE
∴GE=EH
∴四边形EGFH是菱形
∵EF=BC,EF⊥BC
∴BF=EF=CF
∴∠BEF=∠CEF=45°
∴∠BEC=90°
∴四边形EGFH是菱形且∠BEC=90°
∴四边形EGFH是正方形
四、教学反思:
从本节课的授课过程来看,灵活运用了多种教学方法,既有教师的讲解,又有讨论,在教师指导下的自学,组织学生活动等. 调动了学生学习的积极性,充分发挥了学生的主体作用. 课堂拓展了学生的学习空间,给学生充分发表意见的自由度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
18.2.5 正方形 教学设计
一、教学目标:
1.理解正方形的概念;
2.探索正方形的性质与判定,并了解平行四边形、矩形、菱形之间的联系和区别;
3.会应用正方形的性质与判定解决相关证明及计算问题.
二、教学重、难点:
重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
三、教学过程:
情境引入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
知识精讲
正方形的四个角都是_____,四条边都_____.因此,正方形既是______,又是______,它既有______的性质,又有______的性质.
正方形是轴对称图形吗?它的对称轴是什么?
正方形有哪些性质?
实验探究
实验一:利用手中矩形纸片用最快的方法剪出一个正方形.
实验二:如何将一个活动的菱形框变成一个正方形?
思考
1.如果四边形ABCD已经是一个矩形,那么再加上什么条件就可以变为正方形?
2.如果四边形ABCD已经是一个菱形,那么再加上什么条件就可以变为正方形?
3.如果四边形ABCD是一般的平行四边形,那么再加上什么条件就可以变为正方形?
有一组邻边相等的矩形是正方形:有一个角是直角的菱形是正方形;有一组邻边相等且有一个角是直角的平行四边形是正方形.
思考:正方形、菱形、矩形、平行四边形四者之间有什么关系?与同学们讨论一下,能列表或用框图表示出来吗?
典例解析
例1.求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵ 四边形ABCD是正方形
∴ AC=BD,AC⊥BD,AO=BO=CO=DO
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
并且△ABO≌△BCO≌△CDO≌△DAO.
例2.如图,在正方形ABCD中,ΔBEC是等边三角形.求证:∠EAD=∠EDA=15°.
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
【针对练习】四边形ABCD是正方形,以正方形ABCD的一边作等边△ADE,求∠BEC的大小.
解:当等边△ADE在正方形ABCD外部时,如图①,
AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
【点睛】因为等边△ADE与正方形ABCD有一条公共边,所以边相等.本题分两种情况:等边△ADE在正方形的外部或在正方形的内部.
例3.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
解:连接PC,AC.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴AP=PC.
又∵PE⊥BC ,PF⊥DC,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=EF.
【点睛】在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
【针对练习】如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
∴∠DCF=180°-∠BCE=90°.
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
延长BE交DE于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°,
∴∠CBE+∠F=90° ,
∴∠BMF=90°.
∴BE⊥DF.
例4.在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,∠A=∠B=∠C=∠D,AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)=180°-(∠AEN+∠ANE)=180°-90°=90°.
∴四边形EFMN是正方形 .
【针对练习】如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
例5.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB ,∠DAE=∠BAF ,AE=AF ,
∴△ADE≌△ABF(SAS),∴BF=DE;
(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE=AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴得平行四边形AFBE,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.四个角都是直角
C.四条边都相等 D.对角线互相垂直
2.已知四边形ABCD中, ∠A=∠B=∠C=90°, 如果再添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B. AB=CD C. AD=BC D. BC=CD
3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时, 它是矩形 D.当AC=BD时,它是正方形
4.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为( )
A.2 B.4-π C.π D.π-1
5.正方形的一条边长是3,那么它的对角线长是_______.
6.如图,正方形ABCD的两条对角线AC,BD交于点O,点E在BD上,且BE=CD, 则∠BEC的度数为_________.
7.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.
8.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE//CA,DF//BA.
(1)四边形AEDF是______________;
(2)如果∠BAC=90°,那么四边形AEDF是_________;
(3)如果AD平分∠BAC,那么四边形AEDF是_________;
(4)如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是__________.
9.如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连接AF、BD,延长BD交AF于H.求证:BH⊥AF.
10.如图,在正方形ABCD中,Q在CD上,且DQ=CQ,P在BC上,AP=CD+CP,求证: AQ平分∠DAP.
11.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)证明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=BC,证明平行四边形EGFH是正方形.
【参考答案】
B
D
D
B
3
67.5°
2
(1)平行四边形;(2)矩形;(3)菱形;(4)正方形
9.证明:∵四边形AEDC和BCFG是正方形∴AC=DC,CF=CB, ∠ACF=∠BCF=90°
∴△ACF≌△DCB (SAS)
∴∠AFC=∠DBC
又∵∠AFC+∠CAF=90°
∴∠DBC+ ∠CAF=90°
∴∠AHB=90° 即 BH⊥AF
10.证明:延长AQ交BC延长线与E.
∵四边形ABCD是正方形
∴AD=CD,AD// BC
∵∠D=∠QCE,∠DAQ=∠E
又∵DQ=CQ
∴△ADQ≌△ECQ (AAS)
∴AD=CE
∴CD=CE
∴AP=CD+CP=CE+CP=EP
∴∠PAQ=∠E
∴∠PAQ=∠DAQ,即AQ平分∠DAP
11.证明:(1)∵G,F,H分别是BE,BC,CE的中点∴GF//CE,FH//BE
∴GF//EH,FH//GE
∴四边形EGFH是平行四边形
证明:(2)连接EF.
∵BF=CF,EF⊥BC
∴BE=CE
∴GE=EH
∴四边形EGFH是菱形
∵EF=BC,EF⊥BC
∴BF=EF=CF
∴∠BEF=∠CEF=45°
∴∠BEC=90°
∴四边形EGFH是菱形且∠BEC=90°
∴四边形EGFH是正方形
四、教学反思:
从本节课的授课过程来看,灵活运用了多种教学方法,既有教师的讲解,又有讨论,在教师指导下的自学,组织学生活动等. 调动了学生学习的积极性,充分发挥了学生的主体作用. 课堂拓展了学生的学习空间,给学生充分发表意见的自由度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
