人教版八年级数学下册第18章《平行四边形》章节小练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册第18章《平行四边形》章节小练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 471.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 11:49:17 | ||
图片预览



文档简介
八年级数学下册第18章《平行四边形》章节小练习
一、选择题(共8题;共24分)
1.(3分)如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长是30,OE=3,则四边形ABFE的周长是( )
A.21 B.24 C.27 D.18
2.(3分)如果平行四边形的一边长为12,那么这个平行四边形的两条对角线的长可以是 ( )
A.8 和14 B.10 和14 C.18 和20 D.10 和34
3.(3分)如图,在 ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,有下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有10对全等三角形.其中正确的是( )
A.③④ B.①②③ C.①②④ D.①②③④
4.(3分)如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )
A. B. C.3 D.
5.(3分)如图 ABCD的对角线AC,BD相交于点O,E为BC的中点,连结EO并延长,交AD于点F,∠ABC=60°,BC=2AB.给出下列结论:①AB⊥AC.②AD=4OE.③四边形AECF是菱形④其中正确的是( )
A.①②③④ B.①② C.①③ D.②③④
6.(3分)如图,菱形ABCD的两条对角线交于点O,BE⊥DC,交DC的延长线于点E,若AC=6, BD=8,则BE的长是( )
A. B. C. D.4
7.(3分)四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A.1 B. C. D.
8.(3分)如图,在平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC 是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为 ( )
A.-2 B.
C. D.
二、填空题(共10题;共40分)
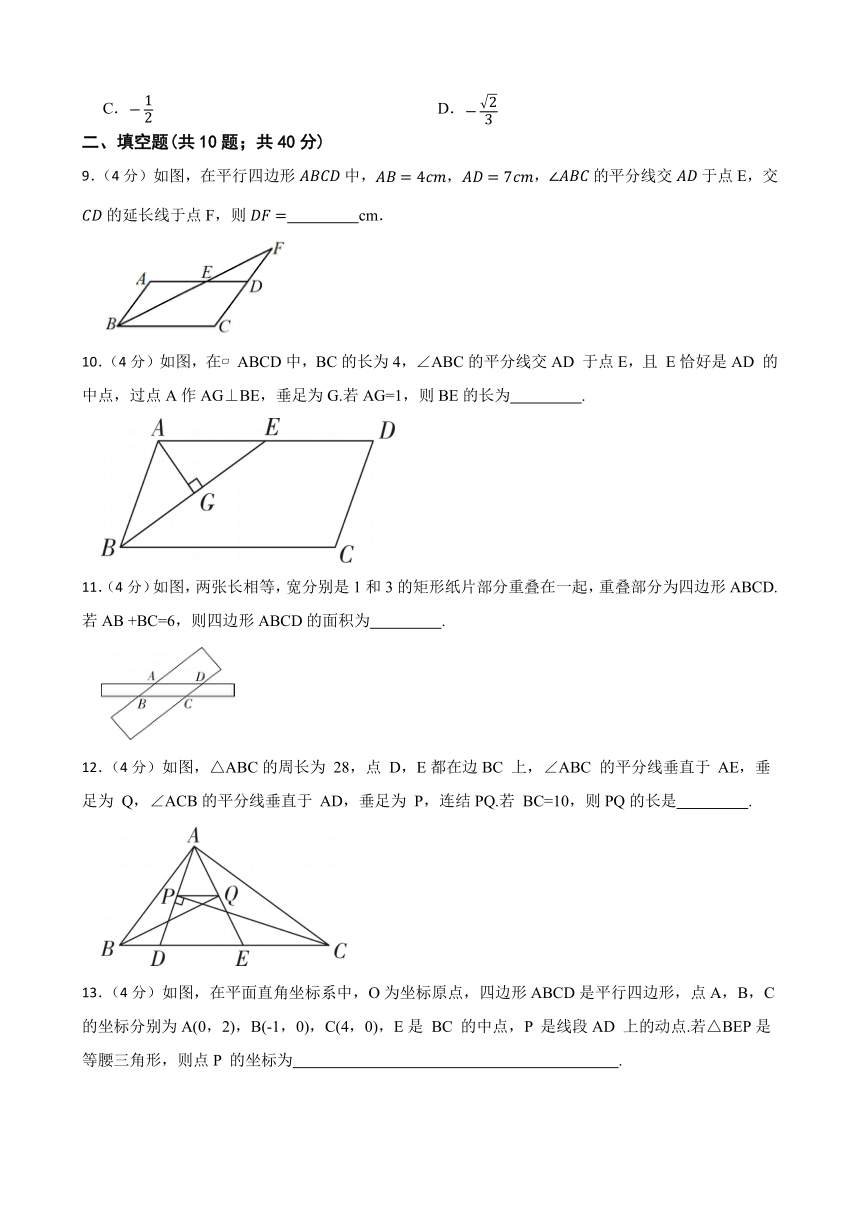
9.(4分)如图,在平行四边形中,,的平分线交于点E,交的延长线于点F,则 cm.
10.(4分)如图,在 ABCD中,BC的长为4,∠ABC的平分线交AD 于点E,且 E恰好是AD 的中点,过点A作AG⊥BE,垂足为G.若AG=1,则BE的长为 .
11.(4分)如图,两张长相等,宽分别是1和3的矩形纸片部分重叠在一起,重叠部分为四边形ABCD.若AB +BC=6,则四边形ABCD的面积为 .
12.(4分)如图,△ABC的周长为 28,点 D,E都在边BC 上,∠ABC 的平分线垂直于 AE,垂足为 Q,∠ACB的平分线垂直于 AD,垂足为 P,连结PQ.若 BC=10,则PQ的长是 .
13.(4分)如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是平行四边形,点A,B,C的坐标分别为A(0,2),B(-1,0),C(4,0),E是 BC 的中点,P 是线段AD 上的动点.若△BEP是等腰三角形,则点P 的坐标为 .
·
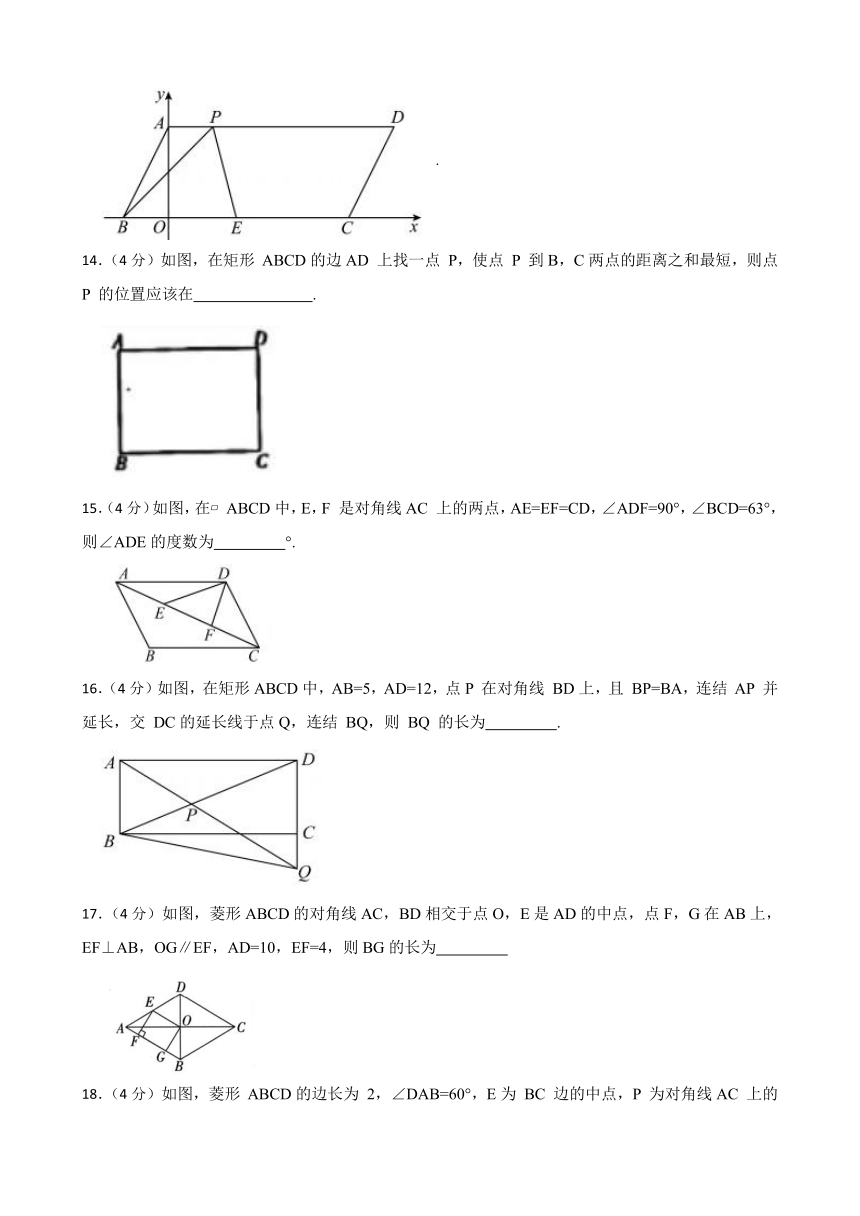
14.(4分)如图,在矩形 ABCD的边AD 上找一点 P,使点 P 到B,C两点的距离之和最短,则点 P 的位置应该在 .
15.(4分)如图,在 ABCD中,E,F 是对角线AC 上的两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的度数为 °.
16.(4分)如图,在矩形ABCD中,AB=5,AD=12,点P 在对角线 BD上,且 BP=BA,连结 AP 并延长,交 DC的延长线于点Q,连结 BQ,则 BQ 的长为 .
17.(4分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF,AD=10,EF=4,则BG的长为
18.(4分)如图,菱形 ABCD的边长为 2,∠DAB=60°,E为 BC 边的中点,P 为对角线AC 上的一个动点,则 PB+PE的最小值为 .
三、解答题(共5题;共38分)
19.(6分)如图,在 ABCD中,点E在AB的延长线上,点F在CD的延长线上,且满足BE=DF.连结EF,分别与BC,AD相交于点G,H.求证:EG=FH.
20.(10分)如图,O为 ABCD的对角线AC 的中点,过点O 作直线 MN,分别交边 AB,CD 于点 M,N,点E,F 在直线MN上,OE=OF,连结AE,CF.
(1)(4分)求证:∠EAM=∠FCN.
(2)(6分)写出图中所有的全等三角形.
21.(6分)如图,点 E,F 分别在 ABCD 的边 BC,AD 连结 BF,DE.求证:四边形 BEDF 是平行四边形.
22.(8分)如图,在 ABCD中,AC,BD相交于点O,且AO=BO,∠ADB的平分线交AB于点E.
(1)(4分)求证: ABCD是矩形.
(2)(4分)若AB=8,OC=5,求AE的长.
23.(8分)如图,在 ABCD中,对角线AC,BD相交于点O,AB=AD.
(1)(4分)求证:AC⊥BD.
(2)(4分)若点E,F分别为AD,AO的中点,连结EF,且求BD的长及四边形ABCD的周长.
答案解析部分
1.A
2.C
3.B
4.B
5.A
6.A
7.B
8.B
9.3
10.2
11.4.5
12.4
13.(0,2)或(3,2)或(,2)或( ,2)
14.AD的中点处
15.21
16.
17.2
18.
19.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠ABC=∠CDA,
∴∠E=∠F,∠EBG=∠FDH,
∵ BE=DF ,
∴△EBG≌△FDH(ASA),
∴EG=FH.
20.(1)证明:∵点O是AC的中点,
∴AO=CO,
在△COF和△AOE中,
∴△COF≌△AOE(SAS)
∴CF=AE,∠CFN=∠AEM,
∵平行四边形ABCD,
∴AB∥CD,
∴∠DNO=∠BMO,
∵∠CNF=∠DNO,∠BMO=∠AME,
∴∠CNF=∠AME,
在△CNF和△AME中
∴△CNF≌△AME(AAS),
∴∠EAM=∠FCN
(2)证明:∵平行四边形ABCD,
∴BC=AD,AB=CD,
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∵DC∥AB,
∴∠NCO=∠MAO
在△NCO和△MAO中
∴△NCO≌△MAO(ASA)
由(1)可知△CNF≌△AME,△COF≌△AOE.
∴图中所有的全等三角形有:△ABC与△CDA,△AOM 与△CON,△AME与△CNF,△AOE 与△COF.
21.证明:∵ 四边形ABCD是平行四边形
∴ AD//BC,AD=BC
又∵,
∴ BE=FD且BE//FD
∴ 四边形 BEDF 是平行四边形.
22.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴OA=OC=OB=OD,即AC=BD,
∴平行四边形ABCD是矩形;
(2)解:过点E作EG⊥BD于点G,如图:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10,
在Rt△ABD中,AD=,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°,
在Rt△ADE和Rt△GDE中,
∴Rt△ADE≌Rt△GDE(HL)
∴AD=GD=6,
∴BG=BD-GD=10-6=4,
在Rt△BEG中,由勾股定理得:
BE2=EG2+BG2,即(8-AE)2=AE2+42,
解得:AE=3.
23.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵AB=AD,
∴AC⊥BD;
(2)解:∵点E,F分别为AD,AO的中点,EF=,
∴OD=2EF=3,
∵四边形ABCD是平行四边形,
∴BD=2OD=6;
由(1)得:AC⊥BD,
∴平行四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵OA=2,
∴AD=,
∴四边形ABCD的周长=4AD=4.
一、选择题(共8题;共24分)
1.(3分)如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长是30,OE=3,则四边形ABFE的周长是( )
A.21 B.24 C.27 D.18
2.(3分)如果平行四边形的一边长为12,那么这个平行四边形的两条对角线的长可以是 ( )
A.8 和14 B.10 和14 C.18 和20 D.10 和34
3.(3分)如图,在 ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,有下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有10对全等三角形.其中正确的是( )
A.③④ B.①②③ C.①②④ D.①②③④
4.(3分)如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )
A. B. C.3 D.
5.(3分)如图 ABCD的对角线AC,BD相交于点O,E为BC的中点,连结EO并延长,交AD于点F,∠ABC=60°,BC=2AB.给出下列结论:①AB⊥AC.②AD=4OE.③四边形AECF是菱形④其中正确的是( )
A.①②③④ B.①② C.①③ D.②③④
6.(3分)如图,菱形ABCD的两条对角线交于点O,BE⊥DC,交DC的延长线于点E,若AC=6, BD=8,则BE的长是( )
A. B. C. D.4
7.(3分)四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A.1 B. C. D.
8.(3分)如图,在平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC 是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为 ( )
A.-2 B.
C. D.
二、填空题(共10题;共40分)
9.(4分)如图,在平行四边形中,,的平分线交于点E,交的延长线于点F,则 cm.
10.(4分)如图,在 ABCD中,BC的长为4,∠ABC的平分线交AD 于点E,且 E恰好是AD 的中点,过点A作AG⊥BE,垂足为G.若AG=1,则BE的长为 .
11.(4分)如图,两张长相等,宽分别是1和3的矩形纸片部分重叠在一起,重叠部分为四边形ABCD.若AB +BC=6,则四边形ABCD的面积为 .
12.(4分)如图,△ABC的周长为 28,点 D,E都在边BC 上,∠ABC 的平分线垂直于 AE,垂足为 Q,∠ACB的平分线垂直于 AD,垂足为 P,连结PQ.若 BC=10,则PQ的长是 .
13.(4分)如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是平行四边形,点A,B,C的坐标分别为A(0,2),B(-1,0),C(4,0),E是 BC 的中点,P 是线段AD 上的动点.若△BEP是等腰三角形,则点P 的坐标为 .
·
14.(4分)如图,在矩形 ABCD的边AD 上找一点 P,使点 P 到B,C两点的距离之和最短,则点 P 的位置应该在 .
15.(4分)如图,在 ABCD中,E,F 是对角线AC 上的两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的度数为 °.
16.(4分)如图,在矩形ABCD中,AB=5,AD=12,点P 在对角线 BD上,且 BP=BA,连结 AP 并延长,交 DC的延长线于点Q,连结 BQ,则 BQ 的长为 .
17.(4分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF,AD=10,EF=4,则BG的长为
18.(4分)如图,菱形 ABCD的边长为 2,∠DAB=60°,E为 BC 边的中点,P 为对角线AC 上的一个动点,则 PB+PE的最小值为 .
三、解答题(共5题;共38分)
19.(6分)如图,在 ABCD中,点E在AB的延长线上,点F在CD的延长线上,且满足BE=DF.连结EF,分别与BC,AD相交于点G,H.求证:EG=FH.
20.(10分)如图,O为 ABCD的对角线AC 的中点,过点O 作直线 MN,分别交边 AB,CD 于点 M,N,点E,F 在直线MN上,OE=OF,连结AE,CF.
(1)(4分)求证:∠EAM=∠FCN.
(2)(6分)写出图中所有的全等三角形.
21.(6分)如图,点 E,F 分别在 ABCD 的边 BC,AD 连结 BF,DE.求证:四边形 BEDF 是平行四边形.
22.(8分)如图,在 ABCD中,AC,BD相交于点O,且AO=BO,∠ADB的平分线交AB于点E.
(1)(4分)求证: ABCD是矩形.
(2)(4分)若AB=8,OC=5,求AE的长.
23.(8分)如图,在 ABCD中,对角线AC,BD相交于点O,AB=AD.
(1)(4分)求证:AC⊥BD.
(2)(4分)若点E,F分别为AD,AO的中点,连结EF,且求BD的长及四边形ABCD的周长.
答案解析部分
1.A
2.C
3.B
4.B
5.A
6.A
7.B
8.B
9.3
10.2
11.4.5
12.4
13.(0,2)或(3,2)或(,2)或( ,2)
14.AD的中点处
15.21
16.
17.2
18.
19.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠ABC=∠CDA,
∴∠E=∠F,∠EBG=∠FDH,
∵ BE=DF ,
∴△EBG≌△FDH(ASA),
∴EG=FH.
20.(1)证明:∵点O是AC的中点,
∴AO=CO,
在△COF和△AOE中,
∴△COF≌△AOE(SAS)
∴CF=AE,∠CFN=∠AEM,
∵平行四边形ABCD,
∴AB∥CD,
∴∠DNO=∠BMO,
∵∠CNF=∠DNO,∠BMO=∠AME,
∴∠CNF=∠AME,
在△CNF和△AME中
∴△CNF≌△AME(AAS),
∴∠EAM=∠FCN
(2)证明:∵平行四边形ABCD,
∴BC=AD,AB=CD,
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∵DC∥AB,
∴∠NCO=∠MAO
在△NCO和△MAO中
∴△NCO≌△MAO(ASA)
由(1)可知△CNF≌△AME,△COF≌△AOE.
∴图中所有的全等三角形有:△ABC与△CDA,△AOM 与△CON,△AME与△CNF,△AOE 与△COF.
21.证明:∵ 四边形ABCD是平行四边形
∴ AD//BC,AD=BC
又∵,
∴ BE=FD且BE//FD
∴ 四边形 BEDF 是平行四边形.
22.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴OA=OC=OB=OD,即AC=BD,
∴平行四边形ABCD是矩形;
(2)解:过点E作EG⊥BD于点G,如图:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10,
在Rt△ABD中,AD=,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°,
在Rt△ADE和Rt△GDE中,
∴Rt△ADE≌Rt△GDE(HL)
∴AD=GD=6,
∴BG=BD-GD=10-6=4,
在Rt△BEG中,由勾股定理得:
BE2=EG2+BG2,即(8-AE)2=AE2+42,
解得:AE=3.
23.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵AB=AD,
∴AC⊥BD;
(2)解:∵点E,F分别为AD,AO的中点,EF=,
∴OD=2EF=3,
∵四边形ABCD是平行四边形,
∴BD=2OD=6;
由(1)得:AC⊥BD,
∴平行四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵OA=2,
∴AD=,
∴四边形ABCD的周长=4AD=4.
