18.2.1 矩形的判定(第二课时)课件(共39张PPT)【2024春人教八下数学同步优质课件含动画】
文档属性
| 名称 | 18.2.1 矩形的判定(第二课时)课件(共39张PPT)【2024春人教八下数学同步优质课件含动画】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览





文档简介
(共39张PPT)
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
18.2 特殊的平行四边形
18.2.2 矩形的判定
第十八章 平行四边形
1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.(重点)
2.能应用矩形的判定解决简单的证明题和计算题.(难点)
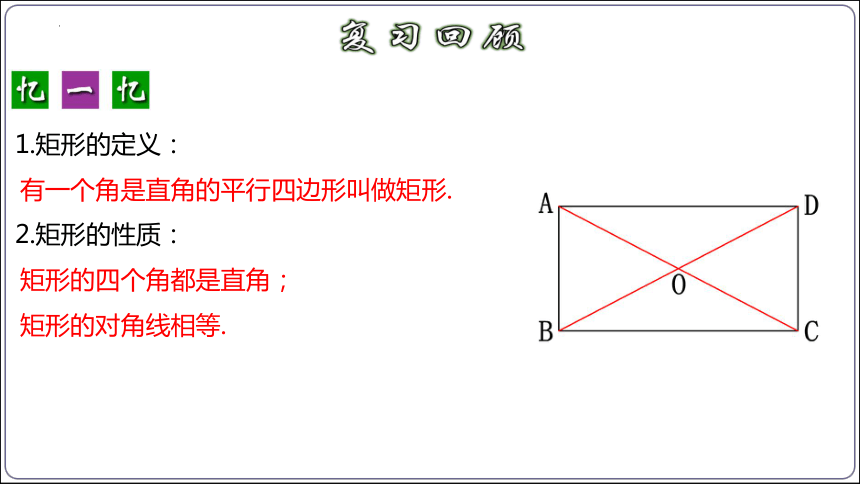
1.矩形的定义:
2.矩形的性质:
有一个角是直角的平行四边形叫做矩形.
矩形的四个角都是直角;
矩形的对角线相等.
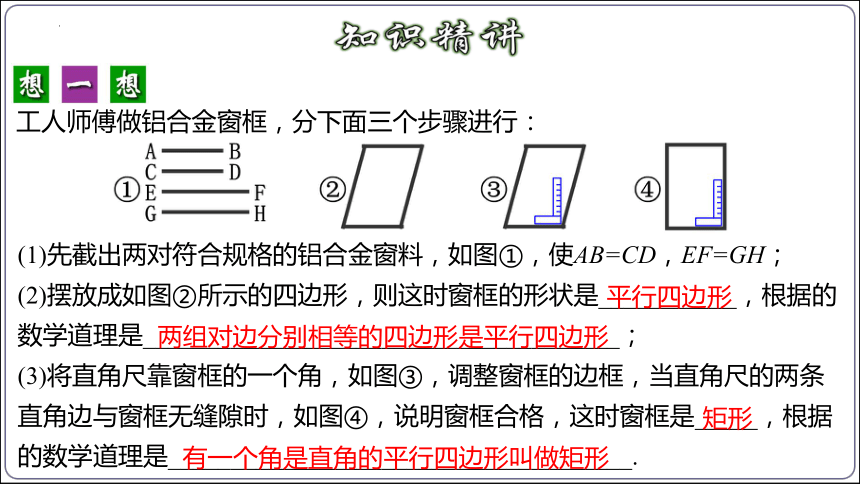
工人师傅做铝合金窗框,分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD,EF=GH;
(2)摆放成如图②所示的四边形,则这时窗框的形状是___________,根据的数学道理是______________________________________;
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图④,说明窗框合格,这时窗框是_____,根据的数学道理是_____________________________________.
平行四边形
两组对边分别相等的四边形是平行四边形
有一个角是直角的平行四边形叫做矩形
矩形
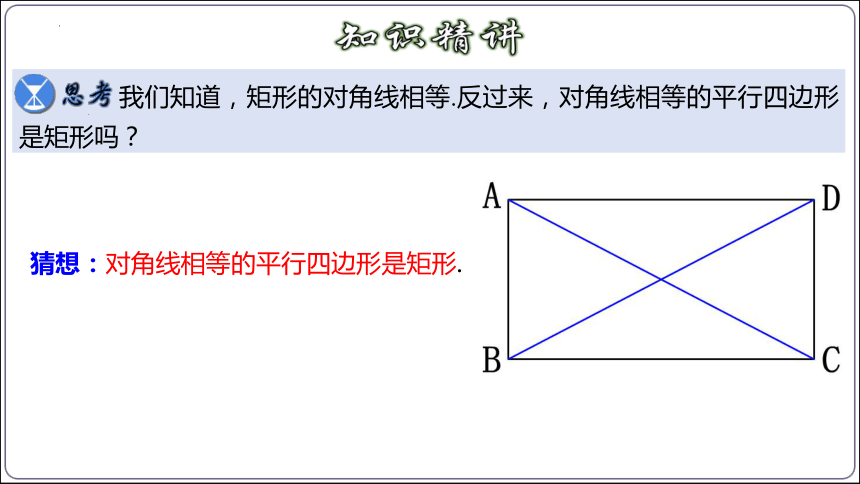
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形. 你知道其中的道理吗?
我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
猜想:对角线相等的平行四边形是矩形.
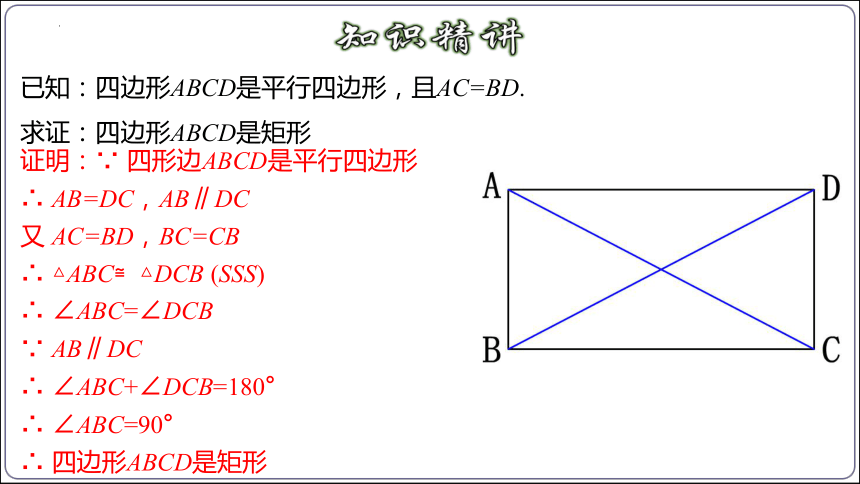
已知:四边形ABCD是平行四边形,且AC=BD.
求证:四边形ABCD是矩形
证明:∵ 四形边ABCD是平行四边形
∴ AB=DC,AB∥DC
又 AC=BD,BC=CB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
∵ AB∥DC
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=90°
∴ 四边形ABCD是矩形
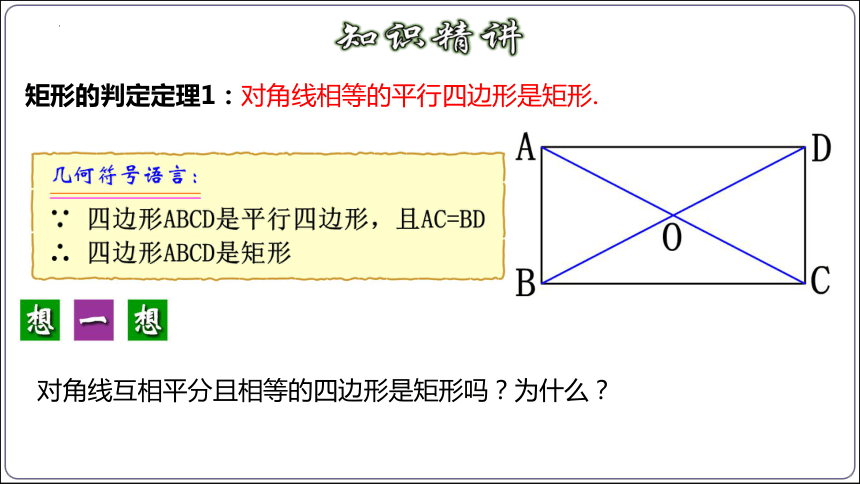
矩形的判定定理1:对角线相等的平行四边形是矩形.
对角线互相平分且相等的四边形是矩形吗?为什么?
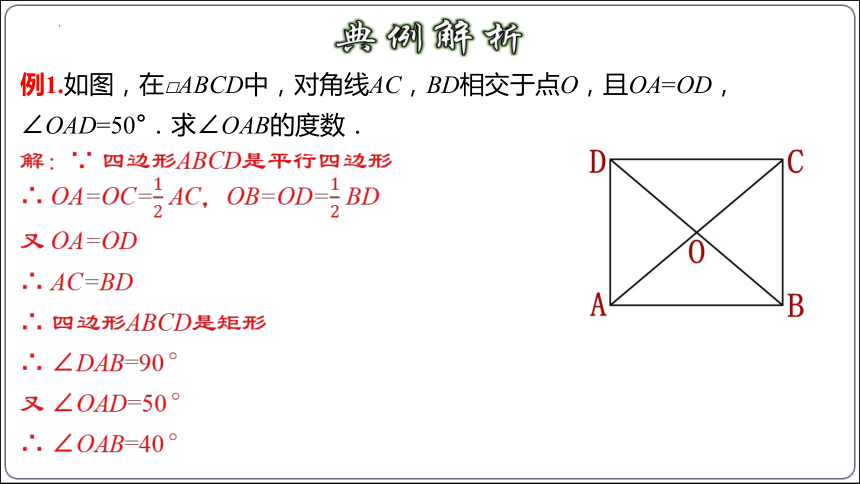
例1.如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵ 四边形ABCD是平行四边形
∴ OA=OC= AC,OB=OD= BD
又 OA=OD
∴ AC=BD
∴ 四边形ABCD是矩形
∴ ∠DAB=90°
又 ∠OAD=50°
∴ ∠OAB=40°
如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,求□ABCD的面积.
解:∵ 四边形ABCD是平行四边形
∴ AC=2AO,BD=2BO
∵ △OAB是等边三角形
∴ AO=BO=AB=4
∴ AC=BD=8
∴ 四边形ABCD是矩形
∴ ∠ABC=90°
∴ 在Rt△ABC中,BC= = =4
∴ S□ABCD=AB×BC=4×4 =16
例2.已知在四边形ABCD中,作AEBC交BD于O点且OB=OD,交DC于点E,连接BE,∠ABD=∠EAB,∠DBE=∠EBC.求证:四边形ABED为矩形.
证明:∵∠ABD=∠EAB,
∴OA=OB,
∵AEBC,
∴∠AEB=∠EBC,
∵∠DBE=∠EBC,
∴∠AEB=∠DBE,
∴OE=OB,
∴OA=OE,
例2.已知在四边形ABCD中,作AEBC交BD于O点且OB=OD,交DC于点E,连接BE,∠ABD=∠EAB,∠DBE=∠EBC.求证:四边形ABED为矩形.
∵OB=OD,
∴四边形ABED是平行四边形,
∵OA=OB,OA=OE,OB=OD,
∴OA=OE=OB=OD,
∴AE=BD,
∴平行四边形ABED为矩形.
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO,
∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
证明:∵四边形ABCD是平行四边形
∴AB // CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
∴∠GBC+∠GCB=(∠ABC+∠BCD) =90°
即∠G=90°
同理∠E=90°,∠AFB=90°
∴∠GFE=90°
∴四边形EFGH是矩形
例3.如图,平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形EFGH是矩形.
已知:如图,P,B,C在同一条直线上,,分别是与的平分线,,E,D为垂足.求证:四边形是矩形.
证明:∵,分别是与的平分线,
,
,
即,
,,
∴四边形是矩形.
例4.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=∠CAM,
∴∠DAE=∠DAC+∠CAE= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
例5.在矩形ABCD中,AB=4,BC=3.若点P是CD上任意一点,如图①,PE⊥BD于点E,PF⊥AC于点F.
(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.
(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系
(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.
(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.
(1)解:连接,如图,
设点到的距离为.
在中,,
由,得
.
四边形是矩形,
,
由,得,
,
化简得.
(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系;
(2)解:,理由见解析,
连接,如下图:
设点到的距离为,
由(1)得,
,
,
.
(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.
(3)解:,理由如下:
连接、,如图.
由
,
,
化简得,
即.
1.在数学活动课.上,老师让同学们判断一个四边形门框是否为矩形,下面是某合作小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B. 测量两组对边是否分别相等
C.测量一组对角是否为直角 D.测量其中三个角是否为直角
2.已知平行四边形ABCD中, 下列条件:①AB=BC; ②AC=BD;③AC⊥BD;④AC平分∠BAD.其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
D
B
3.如图,在□ABCD中,对角线AC、BD相交于点O,且
OA=OB.若AD=4,∠ABD=30°,则AB的长为( )
A.4 B.2 C.8 D. 8
4.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点
D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,
BC=2,AF=BF, 则四边形BCDE的面积是( )
A.2 B.4 C.4 D.2
A
A
5.如图,是四根木棒搭成的平行四边形框架,AB=8cm,
AD=6cm,使AB固定,转动AD,当∠DAB=_____时,
□ABCD的面积最大,此时□ ABCD是_____形,面积
为______cm2.
6.如图,在矩形ABCD中,M为AD边的中点,P为BC
上一点,PE⊥MC,PF⊥ MB, 当AB、BC满足条
件___________时,四边形PEMF为矩形.
90°
矩
48
AB=BC
7.如图,在矩形ABCD中AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF // BC交AB于点F,连接EF,则EF的最小值为______.
证明:设与交于点O,与交于点F,与交于点E,
∵,,
∴点A与点C都在的垂直平分线上,
∴是的垂直平分线,即,
∴,
∵点M,N,N,P,Q分别是,,,的中点,
∴,,
8.已知:如图,在四边形中,,点M,N,P,Q分别是的中点.求证:四边形是矩形.
8.已知:如图,在四边形中,,点M,N,P,Q分别是的中点.求证:四边形是矩形.
∴四边形是平行四边形,
又,
∴四边形是矩形,
∴,
同理:,
∴四边形是矩形.
9.如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(1)若AB=4,BC=3,求AE的长.
(1)解:如图,矩形纸片ABCD中,
∵AB=4,BC=3,
故由勾股定理可得AC=5.
由折叠知:FC=BC=3,∠EFC=∠B=90°,BE=FE.
∴.
设AE=x,则.
在Rt△AFE中,,
解得:.
∴.
9.如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(2)连接DF,若点D,F,E在同一条直线上,且DF=2,求AE的长.
(2)如图,矩形纸片ABCD中,
∵,∴∠DCE=∠BEC,
由折叠知:∠BEC=∠FEC,
∴∠DCE=∠FEC,
∴DC=DE.
又∵点D,F,E在同一条直线上,∠EFC=∠B,
∴∠DFC=90°,
∴∠DFC=∠DAE=90°,
而CF=CB=DA,
∴,∴AE=DF=2.
10.如图,在四边形中,,,,,,动点从点开始沿边向点以的速度运动,动点从点开始沿边向点以的速度运动,动点,分别从点,同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为秒.
(1)当为何值时,四边形为矩形?
(2)当为何值时,四边形为平行四边形?
(1)解:设运动时间为秒,
,,,,
如图1,
,
当时,四边形是平行四边形,
,
四边形是矩形,
即,
解得:,
时,四边形是矩形;
(2)解:如图2,
,
当时,四边形是平行四边形.
此时有,
解得.
当时,四边形是平行四边形.
矩形的判定定理1:对角线相等的平行四边形是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
18.2 特殊的平行四边形
18.2.2 矩形的判定
第十八章 平行四边形
1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.(重点)
2.能应用矩形的判定解决简单的证明题和计算题.(难点)
1.矩形的定义:
2.矩形的性质:
有一个角是直角的平行四边形叫做矩形.
矩形的四个角都是直角;
矩形的对角线相等.
工人师傅做铝合金窗框,分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD,EF=GH;
(2)摆放成如图②所示的四边形,则这时窗框的形状是___________,根据的数学道理是______________________________________;
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图④,说明窗框合格,这时窗框是_____,根据的数学道理是_____________________________________.
平行四边形
两组对边分别相等的四边形是平行四边形
有一个角是直角的平行四边形叫做矩形
矩形
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形. 你知道其中的道理吗?
我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
猜想:对角线相等的平行四边形是矩形.
已知:四边形ABCD是平行四边形,且AC=BD.
求证:四边形ABCD是矩形
证明:∵ 四形边ABCD是平行四边形
∴ AB=DC,AB∥DC
又 AC=BD,BC=CB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
∵ AB∥DC
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=90°
∴ 四边形ABCD是矩形
矩形的判定定理1:对角线相等的平行四边形是矩形.
对角线互相平分且相等的四边形是矩形吗?为什么?
例1.如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵ 四边形ABCD是平行四边形
∴ OA=OC= AC,OB=OD= BD
又 OA=OD
∴ AC=BD
∴ 四边形ABCD是矩形
∴ ∠DAB=90°
又 ∠OAD=50°
∴ ∠OAB=40°
如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,求□ABCD的面积.
解:∵ 四边形ABCD是平行四边形
∴ AC=2AO,BD=2BO
∵ △OAB是等边三角形
∴ AO=BO=AB=4
∴ AC=BD=8
∴ 四边形ABCD是矩形
∴ ∠ABC=90°
∴ 在Rt△ABC中,BC= = =4
∴ S□ABCD=AB×BC=4×4 =16
例2.已知在四边形ABCD中,作AEBC交BD于O点且OB=OD,交DC于点E,连接BE,∠ABD=∠EAB,∠DBE=∠EBC.求证:四边形ABED为矩形.
证明:∵∠ABD=∠EAB,
∴OA=OB,
∵AEBC,
∴∠AEB=∠EBC,
∵∠DBE=∠EBC,
∴∠AEB=∠DBE,
∴OE=OB,
∴OA=OE,
例2.已知在四边形ABCD中,作AEBC交BD于O点且OB=OD,交DC于点E,连接BE,∠ABD=∠EAB,∠DBE=∠EBC.求证:四边形ABED为矩形.
∵OB=OD,
∴四边形ABED是平行四边形,
∵OA=OB,OA=OE,OB=OD,
∴OA=OE=OB=OD,
∴AE=BD,
∴平行四边形ABED为矩形.
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO,
∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
证明:∵四边形ABCD是平行四边形
∴AB // CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
∴∠GBC+∠GCB=(∠ABC+∠BCD) =90°
即∠G=90°
同理∠E=90°,∠AFB=90°
∴∠GFE=90°
∴四边形EFGH是矩形
例3.如图,平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形EFGH是矩形.
已知:如图,P,B,C在同一条直线上,,分别是与的平分线,,E,D为垂足.求证:四边形是矩形.
证明:∵,分别是与的平分线,
,
,
即,
,,
∴四边形是矩形.
例4.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=∠CAM,
∴∠DAE=∠DAC+∠CAE= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
例5.在矩形ABCD中,AB=4,BC=3.若点P是CD上任意一点,如图①,PE⊥BD于点E,PF⊥AC于点F.
(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.
(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系
(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.
(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.
(1)解:连接,如图,
设点到的距离为.
在中,,
由,得
.
四边形是矩形,
,
由,得,
,
化简得.
(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系;
(2)解:,理由见解析,
连接,如下图:
设点到的距离为,
由(1)得,
,
,
.
(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.
(3)解:,理由如下:
连接、,如图.
由
,
,
化简得,
即.
1.在数学活动课.上,老师让同学们判断一个四边形门框是否为矩形,下面是某合作小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B. 测量两组对边是否分别相等
C.测量一组对角是否为直角 D.测量其中三个角是否为直角
2.已知平行四边形ABCD中, 下列条件:①AB=BC; ②AC=BD;③AC⊥BD;④AC平分∠BAD.其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
D
B
3.如图,在□ABCD中,对角线AC、BD相交于点O,且
OA=OB.若AD=4,∠ABD=30°,则AB的长为( )
A.4 B.2 C.8 D. 8
4.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点
D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,
BC=2,AF=BF, 则四边形BCDE的面积是( )
A.2 B.4 C.4 D.2
A
A
5.如图,是四根木棒搭成的平行四边形框架,AB=8cm,
AD=6cm,使AB固定,转动AD,当∠DAB=_____时,
□ABCD的面积最大,此时□ ABCD是_____形,面积
为______cm2.
6.如图,在矩形ABCD中,M为AD边的中点,P为BC
上一点,PE⊥MC,PF⊥ MB, 当AB、BC满足条
件___________时,四边形PEMF为矩形.
90°
矩
48
AB=BC
7.如图,在矩形ABCD中AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF // BC交AB于点F,连接EF,则EF的最小值为______.
证明:设与交于点O,与交于点F,与交于点E,
∵,,
∴点A与点C都在的垂直平分线上,
∴是的垂直平分线,即,
∴,
∵点M,N,N,P,Q分别是,,,的中点,
∴,,
8.已知:如图,在四边形中,,点M,N,P,Q分别是的中点.求证:四边形是矩形.
8.已知:如图,在四边形中,,点M,N,P,Q分别是的中点.求证:四边形是矩形.
∴四边形是平行四边形,
又,
∴四边形是矩形,
∴,
同理:,
∴四边形是矩形.
9.如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(1)若AB=4,BC=3,求AE的长.
(1)解:如图,矩形纸片ABCD中,
∵AB=4,BC=3,
故由勾股定理可得AC=5.
由折叠知:FC=BC=3,∠EFC=∠B=90°,BE=FE.
∴.
设AE=x,则.
在Rt△AFE中,,
解得:.
∴.
9.如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(2)连接DF,若点D,F,E在同一条直线上,且DF=2,求AE的长.
(2)如图,矩形纸片ABCD中,
∵,∴∠DCE=∠BEC,
由折叠知:∠BEC=∠FEC,
∴∠DCE=∠FEC,
∴DC=DE.
又∵点D,F,E在同一条直线上,∠EFC=∠B,
∴∠DFC=90°,
∴∠DFC=∠DAE=90°,
而CF=CB=DA,
∴,∴AE=DF=2.
10.如图,在四边形中,,,,,,动点从点开始沿边向点以的速度运动,动点从点开始沿边向点以的速度运动,动点,分别从点,同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为秒.
(1)当为何值时,四边形为矩形?
(2)当为何值时,四边形为平行四边形?
(1)解:设运动时间为秒,
,,,,
如图1,
,
当时,四边形是平行四边形,
,
四边形是矩形,
即,
解得:,
时,四边形是矩形;
(2)解:如图2,
,
当时,四边形是平行四边形.
此时有,
解得.
当时,四边形是平行四边形.
矩形的判定定理1:对角线相等的平行四边形是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
