18.1.2 平行四边形的判定(第二课时)课件(共29张PPT)【2024春人教八下数学同步优质课件含动画】
文档属性
| 名称 | 18.1.2 平行四边形的判定(第二课时)课件(共29张PPT)【2024春人教八下数学同步优质课件含动画】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
18.1 平行四边形
18.1.4 平行四边形的判定(2)
第十八章 平行四边形
1.掌握“一组对边平行且相等的四边形是平行四边形”的判定方法.(重点)
2.会进行平行四边形的性质与判定的综合运用.(难点)
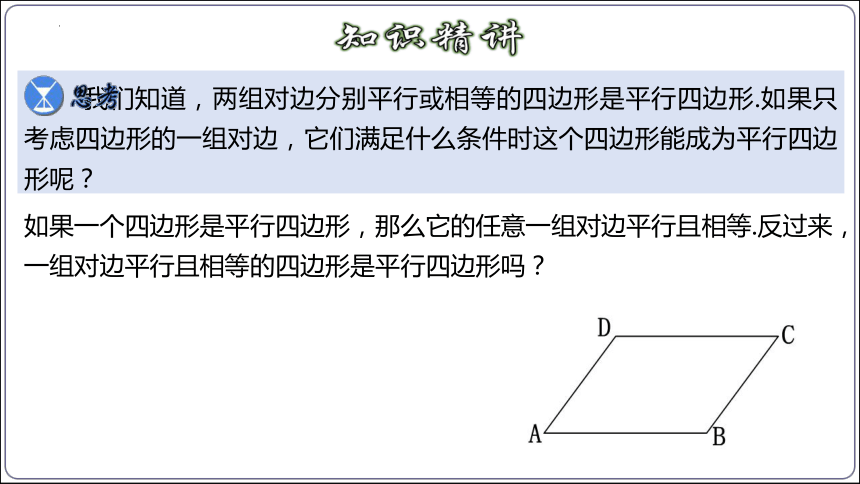
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
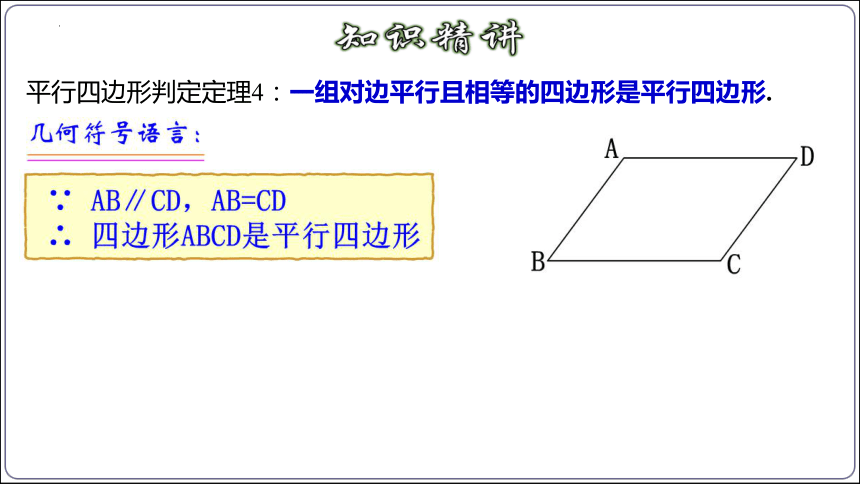
如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵ AB∥CD
∴ ∠1=∠2
又∵ AB=CD,AC=CA
∴ △ABC≌△CDA (SAS)
∴ BC=DA
∴ 四边形ABCD的两组对边分别相等,它是平行四边形.
平行四边形判定定理4:一组对边平行且相等的四边形是平行四边形.
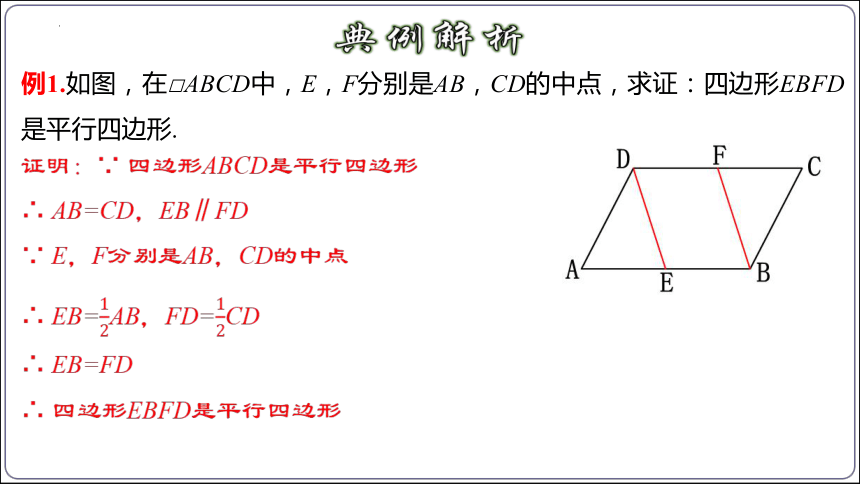
例1.如图,在□ABCD中,E,F分别是AB,CD的中点,求证:四边形EBFD是平行四边形.
证明:∵ 四边形ABCD是平行四边形
∴ AB=CD,EB∥FD
∵ E,F分别是AB,CD的中点
∴ EB=AB,FD=CD
∴ EB=FD
∴ 四边形EBFD是平行四边形
如图,点E,F在□ABCD的边BC,AD上,BE=BC,FD=AD,连接BF,DE.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE=BC,FD=AD,
∴BE=DF.又∵DF∥BE,
∴四边形BEDF是平行四边形.
例2.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
如图,在□ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵ AE⊥BD,CF⊥BD
∴ ∠AED=∠CFB=90°,∠AEF=∠CFE=90°
∴ AE∥CF
∵ 四边形ABCD是平行四边形
∴ AD∥BC,AD=BC
∴ ∠ADE=∠CBF
∴ △ADE≌△CBF (AAS)
∴ AE=CF
∴ 四边形AFCE是平行四边形
例3.如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE,
∴FD=CE.
∵BD平分∠ABC,
∴∠FBD=∠EBD,
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
例4.如图,将□ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
证明:由题意得∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴CE∥D′B,CE=D′B,
∴四边形BCED′是平行四边形.
【点睛】此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=
∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.
1.如图,在四边形ABCD中,AB//CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD B.BC//AD
C.∠A=∠C D.BC=AD
2.如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点,则图中共有平行四边形的个数是( )
A.3 B.4 C.5 D.6
D
B
3.在四边形ABCD中,AB=CD,AB//CD,则下列结论中错误的是( )
A.∠A=∠C B.AD // BC C.∠A=∠B D.对角线互相平分
4.如图,在□ABCD中,E,F分别是边BC,AD上的点,有下列条件:
①AE//CF;②BE=FD;③∠1=∠2;④AE=CF.若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是( )
A.①②③④ B.①②③
C.②③④ D.①③④
C
B
5.已知四边形ABCD,有以下四个条件:①AB//CD;②AB=CD;③BC//AD;
④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有______种.
4
6.(1)在平面直角坐标系中,□ OABC的三个顶点分别为O(0,0)、A(3,0)、B(4,2),则其第四个顶点的坐标是__________.
(2)在平面直角坐标系中,点O、B、D的坐标分别是(0,0)、(5,0)、(2,3),若存在点C,使得以点O、B、D、C为顶点的四边形是平行四边形,则C点的坐标为____________________________.
(1,2)
(3,-3)或(-3,3)或(7,3)
7.如图,已知在□ ABCD中,E、F分别是AD、BC上的点且AE=CF.
求证:BE//FD.
证明:∵四边形ABCD是平行四边形
∴AD=BC,AD//BC
∵AE=CF
∴AD-AE=BC-CF
即DE=BF
又∵ED//BF
∴四边形BFDE是平行四边形
∴BE//FD
8.如图,在□ABCD中,BN=DM,BE=DF,求证:四边形MENF是平行四边形.
证明:∵四边形ABCD是平行四边形
∴BC//AD
∴∠EBN= ∠FDM
∵BN=DM,BE=DF
∴△EBN≌△FDM (SAS)
∴EN=FM,∠BEN= ∠DFM
∴∠FEN=∠EFM
∴EN// FM
∴四边形MENF是平行四边形
9.如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
证明:∵∠ACB=∠CAD=90°,
∴AD∥CE.
∵AE∥DC,
∴四边形AECD是平行四边形.
(2)若AE平分∠BAC,BE=5,BF=4,求AD的长.
解:在Rt△BEF中,
∵BE=5,BF=4,
∴EF===3.
∵AE平分∠BAC,EF⊥AB,∠ACE=90°,
∴EC=EF=3.
由(1)得四边形AECD是平行四边形,
∴AD=EC=3.
10.如图,在四边形ABCD中,AD//BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_________cm;DP=_________cm;
BQ=_________cm;CQ=_________cm.
t
12-t
15-2t
2t
(1)用含t的代数式表示:
AP=_________cm;DP=_________cm;
BQ=_________cm;CQ=_________cm.
(2)当t为何值时,四边形APQB是平行四边形
t
12-t
15-2t
2t
解:(2)∵AD// BC
∴当AP=BQ时,四边形APQB是平行四边形. ∴t=15-2t
解得t=5
∴t=5s时,四边形APQB是平行四边形.
(1)用含t的代数式表示:
AP=_________cm;DP=_________cm;
BQ=_________cm;CQ=_________cm.
(3)当t为何值时,四边形PDCQ是平行四边形
t
12-t
15-2t
2t
解:(3)∵AD//BC
∴当DP=CQ时,四边形PDCQ是平行四边形. ∴12-t=2t
解得t=4
∴t=4s时,四边形PDCQ是平行四边形.
平行四边形判定定理4:一组对边平行且相等的四边形是平行四边形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
18.1 平行四边形
18.1.4 平行四边形的判定(2)
第十八章 平行四边形
1.掌握“一组对边平行且相等的四边形是平行四边形”的判定方法.(重点)
2.会进行平行四边形的性质与判定的综合运用.(难点)
我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵ AB∥CD
∴ ∠1=∠2
又∵ AB=CD,AC=CA
∴ △ABC≌△CDA (SAS)
∴ BC=DA
∴ 四边形ABCD的两组对边分别相等,它是平行四边形.
平行四边形判定定理4:一组对边平行且相等的四边形是平行四边形.
例1.如图,在□ABCD中,E,F分别是AB,CD的中点,求证:四边形EBFD是平行四边形.
证明:∵ 四边形ABCD是平行四边形
∴ AB=CD,EB∥FD
∵ E,F分别是AB,CD的中点
∴ EB=AB,FD=CD
∴ EB=FD
∴ 四边形EBFD是平行四边形
如图,点E,F在□ABCD的边BC,AD上,BE=BC,FD=AD,连接BF,DE.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE=BC,FD=AD,
∴BE=DF.又∵DF∥BE,
∴四边形BEDF是平行四边形.
例2.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
如图,在□ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵ AE⊥BD,CF⊥BD
∴ ∠AED=∠CFB=90°,∠AEF=∠CFE=90°
∴ AE∥CF
∵ 四边形ABCD是平行四边形
∴ AD∥BC,AD=BC
∴ ∠ADE=∠CBF
∴ △ADE≌△CBF (AAS)
∴ AE=CF
∴ 四边形AFCE是平行四边形
例3.如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE,
∴FD=CE.
∵BD平分∠ABC,
∴∠FBD=∠EBD,
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
例4.如图,将□ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
证明:由题意得∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴CE∥D′B,CE=D′B,
∴四边形BCED′是平行四边形.
【点睛】此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=
∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.
1.如图,在四边形ABCD中,AB//CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD B.BC//AD
C.∠A=∠C D.BC=AD
2.如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点,则图中共有平行四边形的个数是( )
A.3 B.4 C.5 D.6
D
B
3.在四边形ABCD中,AB=CD,AB//CD,则下列结论中错误的是( )
A.∠A=∠C B.AD // BC C.∠A=∠B D.对角线互相平分
4.如图,在□ABCD中,E,F分别是边BC,AD上的点,有下列条件:
①AE//CF;②BE=FD;③∠1=∠2;④AE=CF.若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是( )
A.①②③④ B.①②③
C.②③④ D.①③④
C
B
5.已知四边形ABCD,有以下四个条件:①AB//CD;②AB=CD;③BC//AD;
④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有______种.
4
6.(1)在平面直角坐标系中,□ OABC的三个顶点分别为O(0,0)、A(3,0)、B(4,2),则其第四个顶点的坐标是__________.
(2)在平面直角坐标系中,点O、B、D的坐标分别是(0,0)、(5,0)、(2,3),若存在点C,使得以点O、B、D、C为顶点的四边形是平行四边形,则C点的坐标为____________________________.
(1,2)
(3,-3)或(-3,3)或(7,3)
7.如图,已知在□ ABCD中,E、F分别是AD、BC上的点且AE=CF.
求证:BE//FD.
证明:∵四边形ABCD是平行四边形
∴AD=BC,AD//BC
∵AE=CF
∴AD-AE=BC-CF
即DE=BF
又∵ED//BF
∴四边形BFDE是平行四边形
∴BE//FD
8.如图,在□ABCD中,BN=DM,BE=DF,求证:四边形MENF是平行四边形.
证明:∵四边形ABCD是平行四边形
∴BC//AD
∴∠EBN= ∠FDM
∵BN=DM,BE=DF
∴△EBN≌△FDM (SAS)
∴EN=FM,∠BEN= ∠DFM
∴∠FEN=∠EFM
∴EN// FM
∴四边形MENF是平行四边形
9.如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
证明:∵∠ACB=∠CAD=90°,
∴AD∥CE.
∵AE∥DC,
∴四边形AECD是平行四边形.
(2)若AE平分∠BAC,BE=5,BF=4,求AD的长.
解:在Rt△BEF中,
∵BE=5,BF=4,
∴EF===3.
∵AE平分∠BAC,EF⊥AB,∠ACE=90°,
∴EC=EF=3.
由(1)得四边形AECD是平行四边形,
∴AD=EC=3.
10.如图,在四边形ABCD中,AD//BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_________cm;DP=_________cm;
BQ=_________cm;CQ=_________cm.
t
12-t
15-2t
2t
(1)用含t的代数式表示:
AP=_________cm;DP=_________cm;
BQ=_________cm;CQ=_________cm.
(2)当t为何值时,四边形APQB是平行四边形
t
12-t
15-2t
2t
解:(2)∵AD// BC
∴当AP=BQ时,四边形APQB是平行四边形. ∴t=15-2t
解得t=5
∴t=5s时,四边形APQB是平行四边形.
(1)用含t的代数式表示:
AP=_________cm;DP=_________cm;
BQ=_________cm;CQ=_________cm.
(3)当t为何值时,四边形PDCQ是平行四边形
t
12-t
15-2t
2t
解:(3)∵AD//BC
∴当DP=CQ时,四边形PDCQ是平行四边形. ∴12-t=2t
解得t=4
∴t=4s时,四边形PDCQ是平行四边形.
平行四边形判定定理4:一组对边平行且相等的四边形是平行四边形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
