2024年陕西省西交大少年班初试数学试卷(PDF版含解析)
文档属性
| 名称 | 2024年陕西省西交大少年班初试数学试卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 14:02:26 | ||
图片预览



文档简介
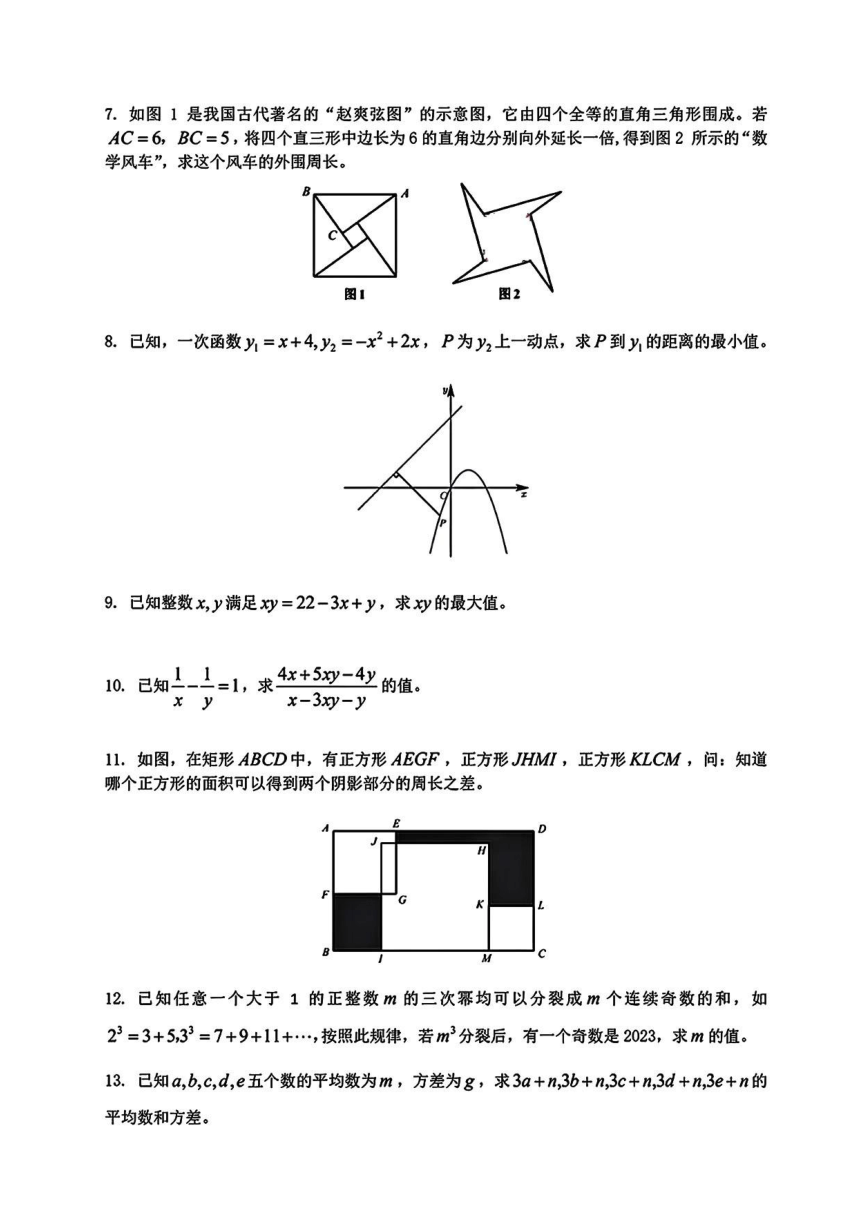
2024年西安交通大学少年班招生初试数学真题
1.已知a+h+c+d=0,ahcd>0,则,以+以
b+c+d a+c+d a+b+d a+b+c
2.已知,在平行四边形ABCD中,E,F分别是BC,CD的中点AE=6,AF=3且
∠EAF=60°,则AB=—0
3.阳光与水平面成60°角,皮球在阳光下的影长为10W3cm,则这个皮球的直径为cm。
4.如图,△ABC,△DEF是等边三角形,边长分别为3、2,求△CDF的内切圆的半径。
5.如图所示,每个方格均为正方形,线段AB与CD交于点P,求sin∠BPD的值。
B
6.如图,正三角形的边长为1,点C与原点重合,现将正三角形向右翻转2023次,求点B在
数轴上对应的数字。
-2-1
0123
7.如图1是我国古代著名的“赵爽弦图”的示意图,它由四个全等的直角三角形围成。若
AC=6,BC=5,将四个直三形中边长为6的直角边分别向外延长一倍,得到图2所示的“数
学风车”,求这个风车的外围周长。
8.已知,一次函数=x+4,y2=-x2+2x,,P为y2上一动点,求P到%的距离的最小值。
9.已知整数x,y满足y=22-3x+y,求y的最大值。
10.已知-1=1,求4x+5y=4y的值。
x y
x-3xy-y
11,如图,在矩形ABCD中,有正方形AEGF,正方形JHMⅡ,正方形KLCM,问:知道
哪个正方形的面积可以得到两个阴影部分的周长之差。
12.已知任意一个大于1的正整数m的三次幂均可以分裂成m个连续奇数的和,如
23=3+5,33=7+9+11+…,按照此规律,若m3分裂后,有一个奇数是2023,求m的值。
13.已知a,b,c,d,e五个数的平均数为m,方差为g,求3a+n,3b+n,3c+n,3d+n,3e+n的
平均数和方差。
14.平面直角坐标系中,已知直线AB:y=-3x
+3,过A作AC垂直于AB,并使AC=AB,
4
求直线BC的解析式。
15.球队两两比赛,主场客场各一场,共42场,问有多少支队伍?
16.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下两种变换:①f(a,b)=(b,a),
如:f(1,3)=(3,1):②g(a,b)=(a,-b),如:g(1,3)=(1,-3):那么f(g(5,-6)=_
17.我们用min表示两个数中的较小数,如min5,3}=3,求minx2-x,2x}的最大值。
18.已知关于x的一元二次方程x2-(n+2)x-2n2=0的解为an,bn,则
2
a-26-2)+
2
2
的值。
(a2-2)(6,-2)(a2024-2)(b2024-2
19.假设队伍中共有2人现列队需要,每10人中走出一个人,当x除以10的余数大于5时,
则在余下的人中再走出一人,则共走出多少人。
[[
20.如图,C为半圆上一点,AB为直径,BC沿BC翻折与AB交于点D,BD沿BD翻折交BC
于E,若E为BC中点,求
的值。
BC
1.已知a+h+c+d=0,ahcd>0,则,以+以
b+c+d a+c+d a+b+d a+b+c
2.已知,在平行四边形ABCD中,E,F分别是BC,CD的中点AE=6,AF=3且
∠EAF=60°,则AB=—0
3.阳光与水平面成60°角,皮球在阳光下的影长为10W3cm,则这个皮球的直径为cm。
4.如图,△ABC,△DEF是等边三角形,边长分别为3、2,求△CDF的内切圆的半径。
5.如图所示,每个方格均为正方形,线段AB与CD交于点P,求sin∠BPD的值。
B
6.如图,正三角形的边长为1,点C与原点重合,现将正三角形向右翻转2023次,求点B在
数轴上对应的数字。
-2-1
0123
7.如图1是我国古代著名的“赵爽弦图”的示意图,它由四个全等的直角三角形围成。若
AC=6,BC=5,将四个直三形中边长为6的直角边分别向外延长一倍,得到图2所示的“数
学风车”,求这个风车的外围周长。
8.已知,一次函数=x+4,y2=-x2+2x,,P为y2上一动点,求P到%的距离的最小值。
9.已知整数x,y满足y=22-3x+y,求y的最大值。
10.已知-1=1,求4x+5y=4y的值。
x y
x-3xy-y
11,如图,在矩形ABCD中,有正方形AEGF,正方形JHMⅡ,正方形KLCM,问:知道
哪个正方形的面积可以得到两个阴影部分的周长之差。
12.已知任意一个大于1的正整数m的三次幂均可以分裂成m个连续奇数的和,如
23=3+5,33=7+9+11+…,按照此规律,若m3分裂后,有一个奇数是2023,求m的值。
13.已知a,b,c,d,e五个数的平均数为m,方差为g,求3a+n,3b+n,3c+n,3d+n,3e+n的
平均数和方差。
14.平面直角坐标系中,已知直线AB:y=-3x
+3,过A作AC垂直于AB,并使AC=AB,
4
求直线BC的解析式。
15.球队两两比赛,主场客场各一场,共42场,问有多少支队伍?
16.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下两种变换:①f(a,b)=(b,a),
如:f(1,3)=(3,1):②g(a,b)=(a,-b),如:g(1,3)=(1,-3):那么f(g(5,-6)=_
17.我们用min表示两个数中的较小数,如min5,3}=3,求minx2-x,2x}的最大值。
18.已知关于x的一元二次方程x2-(n+2)x-2n2=0的解为an,bn,则
2
a-26-2)+
2
2
的值。
(a2-2)(6,-2)(a2024-2)(b2024-2
19.假设队伍中共有2人现列队需要,每10人中走出一个人,当x除以10的余数大于5时,
则在余下的人中再走出一人,则共走出多少人。
[[
20.如图,C为半圆上一点,AB为直径,BC沿BC翻折与AB交于点D,BD沿BD翻折交BC
于E,若E为BC中点,求
的值。
BC
同课章节目录
