人教版数学八下 8.1 二元一次方程组 教案(表格式)
文档属性
| 名称 | 人教版数学八下 8.1 二元一次方程组 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 45.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 00:00:00 | ||
图片预览


文档简介
8.1 二元一次方程组
课题 8.1 二元一次方程组 授课人
教 学 目 标 1.了解二元一次方程、二元一次方程组及其解等有关概念,并会判断一对未知数的值是不是某个二元一次方程组的解. 2.通过对实际问题的分析,使学生进一步体会方程是刻画现实世界的有效数学模型,培养学生良好的数学应用意识. 3.通过具体事例使学生明确什么是二元一次方程和二元一次方程组,在解决问题的过程中,发展学生分析、归纳和概括能力. 4.培养学生使用数学知识解决生活实际问题的能力,同时发展学生的观察、归纳和概括能力.
教学 重点 二元一次方程、二元一次方程组及其解等有关概念,并会判断一对未知数的值是不是某个二元一次方程组的解.
教学 难点 判断一对未知数的值是不是某个二元一次方程组的解.
教学活动
教学 步骤 师生活动 设计意图
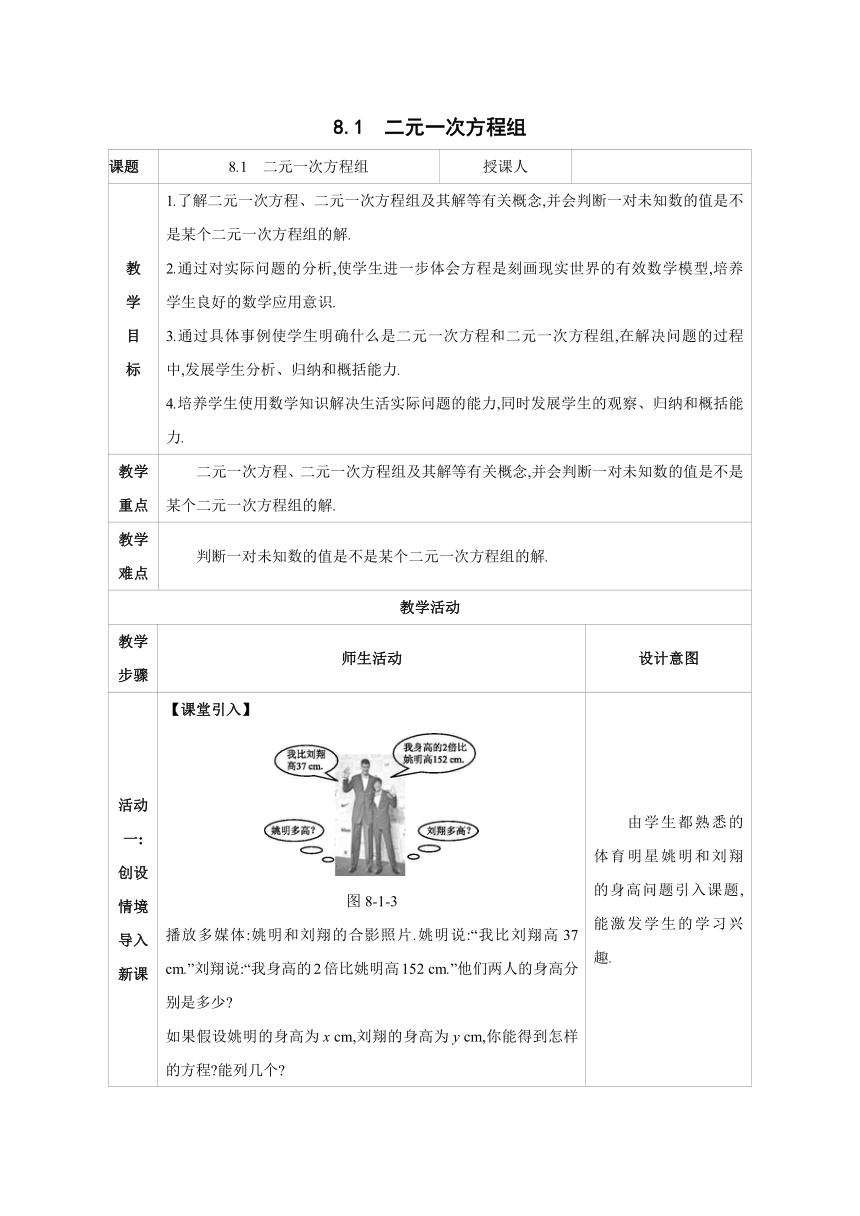
活动 一: 创设 情境 导入 新课 【课堂引入】 图8-1-3 播放多媒体:姚明和刘翔的合影照片.姚明说:“我比刘翔高37 cm.”刘翔说:“我身高的2倍比姚明高152 cm.”他们两人的身高分别是多少 如果假设姚明的身高为x cm,刘翔的身高为y cm,你能得到怎样的方程 能列几个 由学生都熟悉的体育明星姚明和刘翔的身高问题引入课题,能激发学生的学习兴趣.
活动 二: 探究 与 应用 【探究1】 二元一次方程及二元一次方程组 根据以上问题可列出如下方程组: 观察这两个方程,你能对这两个方程的特点做出表述吗
活动 二: 探究 与 应用 学生叙述,然后师生共同归纳二元一次方程的概念:含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程. 判断一个方程是不是二元一次方程,要从元和次两个方面去判断,首先要看元,即未知数是否有两个;其次要看次,即未知数的次数,含有未知数的项的次数必须都是1.二元一次方程的概念分别在元和次两个方面进行了限定,这两个方面缺一不可. 给出二元一次方程组的概念:方程组中有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组. 师生共同总结二元一次方程组的判断要点:首先要看方程组中是不是共含有两个未知数;其次要看含有未知数的项的次数是否都为1.这两个重要条件必须同时满足的两个方程才能称为二元一次方程组. 【应用举例】 例1 有下列方程: ①2x-=1;②+=3;③x2-y2=4;④5(x+y)=7(x-y);⑤2x2=3;⑥x+=4. 其中是二元一次方程的是 ( ) A.① B.①③ C.①④ D.①②④⑥ 学生通过观察、讨论、分析,总结二元一次方程组的概念.通过例题与练习,加强对概念的理解与掌握.
活动 二: 探究 与 应用 例2 下列方程组中,是二元一次方程组的是 ( ) A. B. C. D. 变式1 下列方程哪些是二元一次方程 (1)x+3y-9=0;(2)3x2-2y+12=0;(3)3a-4b=7; (4)3x-=1;(5)3x(x-2y)=5;(6)-5n=1. 变式2 如果方程2xm-1-3y2m+n=1是二元一次方程,那么m= ,n= . 【探究2】 二元一次方程及二元一次方程组的解 根据[课堂引入]内容,可列方程x-y=37①;2y=x+152②.填写下表: 满足方程①,且符合问题的实际意义的x,y的值有哪些 把它们填入表中. xy
问题1:通过填上表,你发现了什么 与同学交流 问题2:什么是一元一次方程的解 你能给出二元一次方程的解的概念吗 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解. 要判断一对未知数的值是不是二元一次方程的解,将两个未知数的值代入二元一次方程的两边,看方程两边的值是否相等,若方程两边的值相等,则这对未知数的值是二元一次方程的解,否则就不是二元一次方程的解. 问题3:一个一元一次方程有几个解 一个二元一次方程呢 一个一元一次方程有1个解. 一个二元一次方程有无数个解. 问题4:什么是二元一次方程组的解 如何确定二元一次方程组中两个方程的公共解 一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解. 判断一对未知数的值是不是二元一次方程组的解,首先要判断此解是不是方程组中每个方程的解,若这对未知数的值是两个方程的公共解,则这对未知数的值就是这个二元一次方程组的解. 通过填表让学生感悟二元一次方程解的不确定性,进而为引入二元一次方程组的解奠定基础.
活动 二: 探究 与 应用 【应用举例】 例3 已知是二元一次方程x+3ky=4的解,则k的值为 ( ) A. B.-3 C. D.2 例4 二元一次方程组的解是 ( ) A. B. C. D. 变式1 下列四组数值中,不是二元一次方程x-3y=1的解的是 ( ) A. B. C. D. 变式2 二元一次方程组的解是 ( ) A. B. C. D. 通过例题与练习,深入理解并掌握二元一次方程(组)的解的概念.
【拓展提升】 例5 某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480名学生刚好住满,设大房间有x个,小房间有y个.下列方程组正确的是 ( ) A. B. C. D. 例6 方程|x+2y-5|+(2x-y+2)2=0可以转化为方程组 . 例7 已知关于x,y的方程(2m-6)x|n|+1+(n+2)=0是二元一次方程,求m,n的值. 已知是方程组的解,则a+b的值为多少 拓展提升,利用二元一次方程(组)的相关知识解决较复杂的问题.
活动 三: 课堂 总结 反思 【当堂训练】 课本第89页练习. 【课后作业】 课本第90页习题8.1第1,3,4,5题. 通过练习进一步巩固二元一次方程(组)的知识.
课题 8.1 二元一次方程组 授课人
教 学 目 标 1.了解二元一次方程、二元一次方程组及其解等有关概念,并会判断一对未知数的值是不是某个二元一次方程组的解. 2.通过对实际问题的分析,使学生进一步体会方程是刻画现实世界的有效数学模型,培养学生良好的数学应用意识. 3.通过具体事例使学生明确什么是二元一次方程和二元一次方程组,在解决问题的过程中,发展学生分析、归纳和概括能力. 4.培养学生使用数学知识解决生活实际问题的能力,同时发展学生的观察、归纳和概括能力.
教学 重点 二元一次方程、二元一次方程组及其解等有关概念,并会判断一对未知数的值是不是某个二元一次方程组的解.
教学 难点 判断一对未知数的值是不是某个二元一次方程组的解.
教学活动
教学 步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 图8-1-3 播放多媒体:姚明和刘翔的合影照片.姚明说:“我比刘翔高37 cm.”刘翔说:“我身高的2倍比姚明高152 cm.”他们两人的身高分别是多少 如果假设姚明的身高为x cm,刘翔的身高为y cm,你能得到怎样的方程 能列几个 由学生都熟悉的体育明星姚明和刘翔的身高问题引入课题,能激发学生的学习兴趣.
活动 二: 探究 与 应用 【探究1】 二元一次方程及二元一次方程组 根据以上问题可列出如下方程组: 观察这两个方程,你能对这两个方程的特点做出表述吗
活动 二: 探究 与 应用 学生叙述,然后师生共同归纳二元一次方程的概念:含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程. 判断一个方程是不是二元一次方程,要从元和次两个方面去判断,首先要看元,即未知数是否有两个;其次要看次,即未知数的次数,含有未知数的项的次数必须都是1.二元一次方程的概念分别在元和次两个方面进行了限定,这两个方面缺一不可. 给出二元一次方程组的概念:方程组中有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组. 师生共同总结二元一次方程组的判断要点:首先要看方程组中是不是共含有两个未知数;其次要看含有未知数的项的次数是否都为1.这两个重要条件必须同时满足的两个方程才能称为二元一次方程组. 【应用举例】 例1 有下列方程: ①2x-=1;②+=3;③x2-y2=4;④5(x+y)=7(x-y);⑤2x2=3;⑥x+=4. 其中是二元一次方程的是 ( ) A.① B.①③ C.①④ D.①②④⑥ 学生通过观察、讨论、分析,总结二元一次方程组的概念.通过例题与练习,加强对概念的理解与掌握.
活动 二: 探究 与 应用 例2 下列方程组中,是二元一次方程组的是 ( ) A. B. C. D. 变式1 下列方程哪些是二元一次方程 (1)x+3y-9=0;(2)3x2-2y+12=0;(3)3a-4b=7; (4)3x-=1;(5)3x(x-2y)=5;(6)-5n=1. 变式2 如果方程2xm-1-3y2m+n=1是二元一次方程,那么m= ,n= . 【探究2】 二元一次方程及二元一次方程组的解 根据[课堂引入]内容,可列方程x-y=37①;2y=x+152②.填写下表: 满足方程①,且符合问题的实际意义的x,y的值有哪些 把它们填入表中. xy
问题1:通过填上表,你发现了什么 与同学交流 问题2:什么是一元一次方程的解 你能给出二元一次方程的解的概念吗 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解. 要判断一对未知数的值是不是二元一次方程的解,将两个未知数的值代入二元一次方程的两边,看方程两边的值是否相等,若方程两边的值相等,则这对未知数的值是二元一次方程的解,否则就不是二元一次方程的解. 问题3:一个一元一次方程有几个解 一个二元一次方程呢 一个一元一次方程有1个解. 一个二元一次方程有无数个解. 问题4:什么是二元一次方程组的解 如何确定二元一次方程组中两个方程的公共解 一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解. 判断一对未知数的值是不是二元一次方程组的解,首先要判断此解是不是方程组中每个方程的解,若这对未知数的值是两个方程的公共解,则这对未知数的值就是这个二元一次方程组的解. 通过填表让学生感悟二元一次方程解的不确定性,进而为引入二元一次方程组的解奠定基础.
活动 二: 探究 与 应用 【应用举例】 例3 已知是二元一次方程x+3ky=4的解,则k的值为 ( ) A. B.-3 C. D.2 例4 二元一次方程组的解是 ( ) A. B. C. D. 变式1 下列四组数值中,不是二元一次方程x-3y=1的解的是 ( ) A. B. C. D. 变式2 二元一次方程组的解是 ( ) A. B. C. D. 通过例题与练习,深入理解并掌握二元一次方程(组)的解的概念.
【拓展提升】 例5 某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480名学生刚好住满,设大房间有x个,小房间有y个.下列方程组正确的是 ( ) A. B. C. D. 例6 方程|x+2y-5|+(2x-y+2)2=0可以转化为方程组 . 例7 已知关于x,y的方程(2m-6)x|n|+1+(n+2)=0是二元一次方程,求m,n的值. 已知是方程组的解,则a+b的值为多少 拓展提升,利用二元一次方程(组)的相关知识解决较复杂的问题.
活动 三: 课堂 总结 反思 【当堂训练】 课本第89页练习. 【课后作业】 课本第90页习题8.1第1,3,4,5题. 通过练习进一步巩固二元一次方程(组)的知识.
