数学人教A版(2019)必修第二册6.1平面向量的概念 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.1平面向量的概念 课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 14:20:42 | ||
图片预览





文档简介
(共25张PPT)
人教版必修第二册A版
6.1《 平面向量的概念 》
( 2 课 时 )
教学目标
学习目标:1.认识平面向量的实际背景,理解平面向量的相关概念(数学抽象);
2.理解与掌握平面向量的表示方法与特殊关系,并能灵活运用其来求解相关的实际问题(数学抽象、逻辑推理).
教学重点:平面向量的表示方法与特殊关系;
教学难点:平面向量的特殊关系.
一
情景问题——现实生活中的量(导学)
(一)情景:现实生活中的量
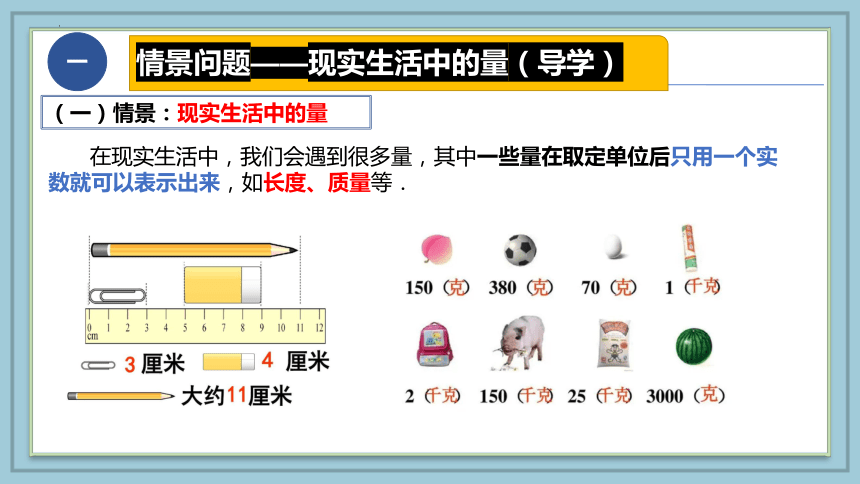
在现实生活中,我们会遇到很多量,其中一些量在取定单位后只用一个实数就可以表示出来,如长度、质量等.
一
情景问题——现实生活中的量(导学)
(一)情景:现实生活中的量
生活中还有一些量则不是这样,例如右图中小船的位移,小船由地向东南方向航行15海里)到达地(速度的大小为) . 这里,如果仅指出 “由地航行15海里)”(即位移的大小), 而不指明 “向东南方向”航行(即位移的方向),那么小船就不一定到达B地.
这就说明,位移是既有大小又有方向的量.
一
情景问题——现实生活中的量(导学)
(一)情景:现实生活中的量
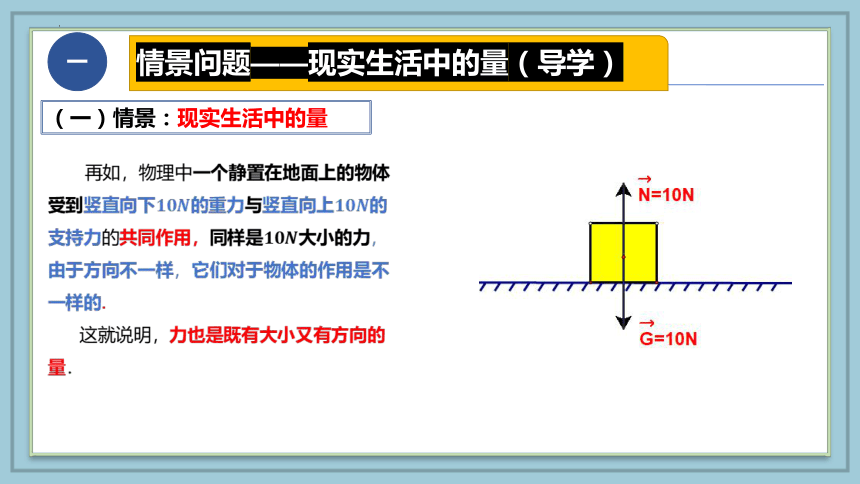
再如,物理中一个静置在地面上的物体受到竖直向下的重力与竖直向上的支持力的共同作用,同样是大小的力,由于方向不一样,它们对于物体的作用是不一样的.
这就说明,力也是既有大小又有方向的量.
一
情景问题——现实生活中的量(导学)
(二)问题
同学们,刚才大家发现生活中有两种不同的量,它们有什么本质的区别?在数学和物理上,我们又分别用什么概念来描述它们呢?相信各位同学通过今天的学习,将会对这些生活中的量有更加深刻的认识.
二
探究新知1——向量的概念(互学)
(一)向量的定义
像力、位移这样,在数学中, 我们把既有大小又有方向的量叫做向量.
像长度、质量这样,在数学中,我们把只有大小没有方向的量叫做数量.
(二)数量的定义
注:物理学中常称向量为矢量,数量为标量,你还能举出物理学中其他的一些向量和数量吗?
三
小组合作、讨论交流1(自学)
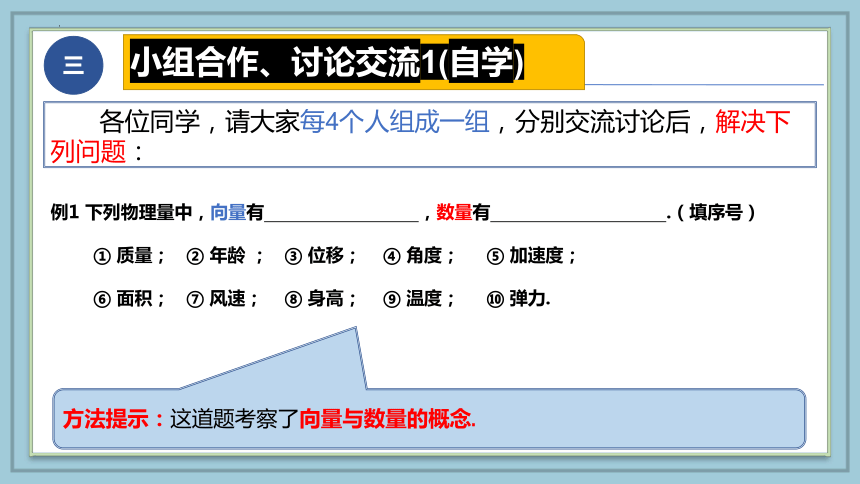
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
例1 下列物理量中,向量有 ,数量有 .(填序号)
① 质量; ② 年龄 ; ③ 位移; ④ 角度; ⑤ 加速度;
⑥ 面积; ⑦ 风速; ⑧ 身高; ⑨ 温度; ⑩ 弹力.
方法提示:这道题考察了向量与数量的概念.
四
成果展示1(迁移变通)
例1 下列物理量中,向量有 ,数量有 .(填序号)
①质量; ②年龄 ; ③ 位移; ④角度; ⑤加速度;
⑥面积; ⑦风速; ⑧身高; ⑨温度; ⑩弹力.
③⑤⑦⑩
①②④⑥⑧⑨
五
探究新知2——向量的表示与特殊向量(互学)
(一)问题
数量可以用一个实数表示,而实数与数轴上的点一一对应,所以数量可用数轴上的点表示,而且不同的点表示不同的数量.
例如,某物体的质量为,可用数轴上的点表示如下图所示:
思考:那么,我们应该如何表示向量呢?
探究新知2——向量的表示与特殊向量(互学)
(二)探究
小船由地向东南方向航行15海里)到达地(速度的大小为),小船的位移可以表示为:
以为起点,为终点,我们可以用连接两点的线段长度代表小船行进的距离,并在终点处加上箭头表示小船行驶的方向.于是,这条“带有方向的线段”就可以用来表示位移.
受此启发,我们可以用带箭头的线段来表示向量:线段按一定比例(标度)画出,它的长短表示向量的大小,箭头的指向表示向量的方向.
五
探究新知2——向量的表示与特殊向量(互学)
(三)有向线段
1.定义
如图所示,我们把具有方向的线段叫做有向线段.
以为起点、为终点的有向线段记作,线段 AB的长度也叫做有向线段的模,记作.
2.三要素
有向线段包含三个要素:起点、方向、长度.
注:知道了有向线段的起点、方向和长度,它的终点就唯一确定了.
五
探究新知2——向量的表示与特殊向量(互学)
(四)向量的表示
1.向量的几何表示
如图,数学上通常用有向线段表示向量,以为起点、为终点的有向线段表示向量.
其中有向线段的长度表示向量的大小(或模)记作,有向线段的方向表示向量的方向.
注:在空间中,向量是可以进行平移的.
2.向量的代数表示
数学上也可以用黑体的小写字母(印刷体)或带箭头的小写字母(手写体)表示向量.
例如 ,向量
五
探究新知2——向量的表示与特殊向量(互学)
(五)特殊向量
1.零向量
长度为 0 的向量叫做零向量 , 记作 0(或 ).
注:① 的模为0,即 ;
② 的方向是任意的,即它的方向可以看作任意方向.
五
2.单位向量
长度等于1个单位长度的向量,叫做单位向量 ,
通常用 表示,即 .
注:任何一个非零向量 都有它的单位向量,且
六
小组合作、讨论交流2(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了向量的表示以及向量的长度(或模).
例2 在图 6.1 4中,分别用向量表示 地至 两地的位移,并根据图中的比例尺,求出 地至 两地的实际距离(精确到) .
1:8 000 000
七
成果展示2(迁移变通)
例2 在图 6.1 4中,分别用向量表示 地至 两地的位移,并根据图中的比例尺,求出 地至 两地的实际距离(精确到) .
解:如图所示
表示表示 地至 地的位移,
表示表示 地至 地的位移,
∵ 图中比例尺为1:8 000 000
即图上 代表实际距离
∴
答: 地至 两地的实际距离分别约为.
探究新知3——向量间的特殊关系(互学)
(一)平行向量(或共线向量)
方向相同或相反的非零向量叫做平行向量(或共线向量),记作 .
注① 我们规定,零向量与任意向量平行, 即对于任意向量 ,都有 .
八
注② 如图,已知 是一组平行向量,任作一条与 所在直线平行的直线,在 上任取一点,则可在上分别作出 ,.
这就是说,任一组平行向量都可以平移到同一条直线上, 因此,平行向量也叫做共线向量 .
探究新知3——向量间的特殊关系(互学)
(二)相等向量
长度相等且方向相同的向量叫做相等向量. 如图 向量为相等向量,记作 .
注:①任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关;
② 同时,两条方向相同且长度相等的有向线段表示同一个向量, 因为向量完全由它的模和方向确定.
八
探究新知3——向量间的特殊关系(互学)
(三)相反向量
长度相等且方向相反的向量叫做相反向量. 如图 向量为相反向量,记作 .
注①向量 的相反向量为,且 ;
注②规定: 的相反向量为 ,记作.
八
九
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了共线向量与相等向量.
例3 如图 , 设是正六边形的中心.
(1) 写出图中的共线向量;
(2) 分别写出图中与相等的向量.
十
成果展示3(迁移变通)
解:(1)如图所示
∵ 已知是正六边形的中心
∴ , , 是共线向量
, , 是共线向量
, , 是共线向量
(2)由图可知
; =;= =
例3 如图 , 设是正六边形的中心.
(1) 写出图中的共线向量;
(2) 分别写出图中与相等的向量.
十一
提升演练(检测实践)
题型一 平面向量概念的综合运用
例1 已知下列命题:①单位向量都相等;②两个有共同起点且长度相等的非零向量,它们的终点必相同;③由于0方向不确定,故0不能与任意向量平行;④如果则 ⑤如果,则与的方向相同
其中不正确的命题是 .(把不正确命题的序号都填上)
①②③⑤
课堂小结
十二
今天我们学习了哪些内容?
1.认识与理解了平面向量的实际背景,以及平面向量的相关概念;
2.理解与掌握了平面向量的表示方法、特殊向量与向量间的特殊关系,并能灵活运用其来求解相关的实际问题.
十三
学生自评
请小老师组对所负责组员的课堂表现进行评价
十四
家庭作业
1.整理导学案中本节课知识点并记背;
2.完成导学案上相关题型.
人教版必修第二册A版
6.1《 平面向量的概念 》
( 2 课 时 )
教学目标
学习目标:1.认识平面向量的实际背景,理解平面向量的相关概念(数学抽象);
2.理解与掌握平面向量的表示方法与特殊关系,并能灵活运用其来求解相关的实际问题(数学抽象、逻辑推理).
教学重点:平面向量的表示方法与特殊关系;
教学难点:平面向量的特殊关系.
一
情景问题——现实生活中的量(导学)
(一)情景:现实生活中的量
在现实生活中,我们会遇到很多量,其中一些量在取定单位后只用一个实数就可以表示出来,如长度、质量等.
一
情景问题——现实生活中的量(导学)
(一)情景:现实生活中的量
生活中还有一些量则不是这样,例如右图中小船的位移,小船由地向东南方向航行15海里)到达地(速度的大小为) . 这里,如果仅指出 “由地航行15海里)”(即位移的大小), 而不指明 “向东南方向”航行(即位移的方向),那么小船就不一定到达B地.
这就说明,位移是既有大小又有方向的量.
一
情景问题——现实生活中的量(导学)
(一)情景:现实生活中的量
再如,物理中一个静置在地面上的物体受到竖直向下的重力与竖直向上的支持力的共同作用,同样是大小的力,由于方向不一样,它们对于物体的作用是不一样的.
这就说明,力也是既有大小又有方向的量.
一
情景问题——现实生活中的量(导学)
(二)问题
同学们,刚才大家发现生活中有两种不同的量,它们有什么本质的区别?在数学和物理上,我们又分别用什么概念来描述它们呢?相信各位同学通过今天的学习,将会对这些生活中的量有更加深刻的认识.
二
探究新知1——向量的概念(互学)
(一)向量的定义
像力、位移这样,在数学中, 我们把既有大小又有方向的量叫做向量.
像长度、质量这样,在数学中,我们把只有大小没有方向的量叫做数量.
(二)数量的定义
注:物理学中常称向量为矢量,数量为标量,你还能举出物理学中其他的一些向量和数量吗?
三
小组合作、讨论交流1(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
例1 下列物理量中,向量有 ,数量有 .(填序号)
① 质量; ② 年龄 ; ③ 位移; ④ 角度; ⑤ 加速度;
⑥ 面积; ⑦ 风速; ⑧ 身高; ⑨ 温度; ⑩ 弹力.
方法提示:这道题考察了向量与数量的概念.
四
成果展示1(迁移变通)
例1 下列物理量中,向量有 ,数量有 .(填序号)
①质量; ②年龄 ; ③ 位移; ④角度; ⑤加速度;
⑥面积; ⑦风速; ⑧身高; ⑨温度; ⑩弹力.
③⑤⑦⑩
①②④⑥⑧⑨
五
探究新知2——向量的表示与特殊向量(互学)
(一)问题
数量可以用一个实数表示,而实数与数轴上的点一一对应,所以数量可用数轴上的点表示,而且不同的点表示不同的数量.
例如,某物体的质量为,可用数轴上的点表示如下图所示:
思考:那么,我们应该如何表示向量呢?
探究新知2——向量的表示与特殊向量(互学)
(二)探究
小船由地向东南方向航行15海里)到达地(速度的大小为),小船的位移可以表示为:
以为起点,为终点,我们可以用连接两点的线段长度代表小船行进的距离,并在终点处加上箭头表示小船行驶的方向.于是,这条“带有方向的线段”就可以用来表示位移.
受此启发,我们可以用带箭头的线段来表示向量:线段按一定比例(标度)画出,它的长短表示向量的大小,箭头的指向表示向量的方向.
五
探究新知2——向量的表示与特殊向量(互学)
(三)有向线段
1.定义
如图所示,我们把具有方向的线段叫做有向线段.
以为起点、为终点的有向线段记作,线段 AB的长度也叫做有向线段的模,记作.
2.三要素
有向线段包含三个要素:起点、方向、长度.
注:知道了有向线段的起点、方向和长度,它的终点就唯一确定了.
五
探究新知2——向量的表示与特殊向量(互学)
(四)向量的表示
1.向量的几何表示
如图,数学上通常用有向线段表示向量,以为起点、为终点的有向线段表示向量.
其中有向线段的长度表示向量的大小(或模)记作,有向线段的方向表示向量的方向.
注:在空间中,向量是可以进行平移的.
2.向量的代数表示
数学上也可以用黑体的小写字母(印刷体)或带箭头的小写字母(手写体)表示向量.
例如 ,向量
五
探究新知2——向量的表示与特殊向量(互学)
(五)特殊向量
1.零向量
长度为 0 的向量叫做零向量 , 记作 0(或 ).
注:① 的模为0,即 ;
② 的方向是任意的,即它的方向可以看作任意方向.
五
2.单位向量
长度等于1个单位长度的向量,叫做单位向量 ,
通常用 表示,即 .
注:任何一个非零向量 都有它的单位向量,且
六
小组合作、讨论交流2(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了向量的表示以及向量的长度(或模).
例2 在图 6.1 4中,分别用向量表示 地至 两地的位移,并根据图中的比例尺,求出 地至 两地的实际距离(精确到) .
1:8 000 000
七
成果展示2(迁移变通)
例2 在图 6.1 4中,分别用向量表示 地至 两地的位移,并根据图中的比例尺,求出 地至 两地的实际距离(精确到) .
解:如图所示
表示表示 地至 地的位移,
表示表示 地至 地的位移,
∵ 图中比例尺为1:8 000 000
即图上 代表实际距离
∴
答: 地至 两地的实际距离分别约为.
探究新知3——向量间的特殊关系(互学)
(一)平行向量(或共线向量)
方向相同或相反的非零向量叫做平行向量(或共线向量),记作 .
注① 我们规定,零向量与任意向量平行, 即对于任意向量 ,都有 .
八
注② 如图,已知 是一组平行向量,任作一条与 所在直线平行的直线,在 上任取一点,则可在上分别作出 ,.
这就是说,任一组平行向量都可以平移到同一条直线上, 因此,平行向量也叫做共线向量 .
探究新知3——向量间的特殊关系(互学)
(二)相等向量
长度相等且方向相同的向量叫做相等向量. 如图 向量为相等向量,记作 .
注:①任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关;
② 同时,两条方向相同且长度相等的有向线段表示同一个向量, 因为向量完全由它的模和方向确定.
八
探究新知3——向量间的特殊关系(互学)
(三)相反向量
长度相等且方向相反的向量叫做相反向量. 如图 向量为相反向量,记作 .
注①向量 的相反向量为,且 ;
注②规定: 的相反向量为 ,记作.
八
九
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了共线向量与相等向量.
例3 如图 , 设是正六边形的中心.
(1) 写出图中的共线向量;
(2) 分别写出图中与相等的向量.
十
成果展示3(迁移变通)
解:(1)如图所示
∵ 已知是正六边形的中心
∴ , , 是共线向量
, , 是共线向量
, , 是共线向量
(2)由图可知
; =;= =
例3 如图 , 设是正六边形的中心.
(1) 写出图中的共线向量;
(2) 分别写出图中与相等的向量.
十一
提升演练(检测实践)
题型一 平面向量概念的综合运用
例1 已知下列命题:①单位向量都相等;②两个有共同起点且长度相等的非零向量,它们的终点必相同;③由于0方向不确定,故0不能与任意向量平行;④如果则 ⑤如果,则与的方向相同
其中不正确的命题是 .(把不正确命题的序号都填上)
①②③⑤
课堂小结
十二
今天我们学习了哪些内容?
1.认识与理解了平面向量的实际背景,以及平面向量的相关概念;
2.理解与掌握了平面向量的表示方法、特殊向量与向量间的特殊关系,并能灵活运用其来求解相关的实际问题.
十三
学生自评
请小老师组对所负责组员的课堂表现进行评价
十四
家庭作业
1.整理导学案中本节课知识点并记背;
2.完成导学案上相关题型.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
