微专题 求与圆有关的不规则图形面积的方法-2024年中考数学复习课件(共27张PPT)
文档属性
| 名称 | 微专题 求与圆有关的不规则图形面积的方法-2024年中考数学复习课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 16:59:21 | ||
图片预览






文档简介
(共27张PPT)
求与圆有关的不规则图形面积的方法
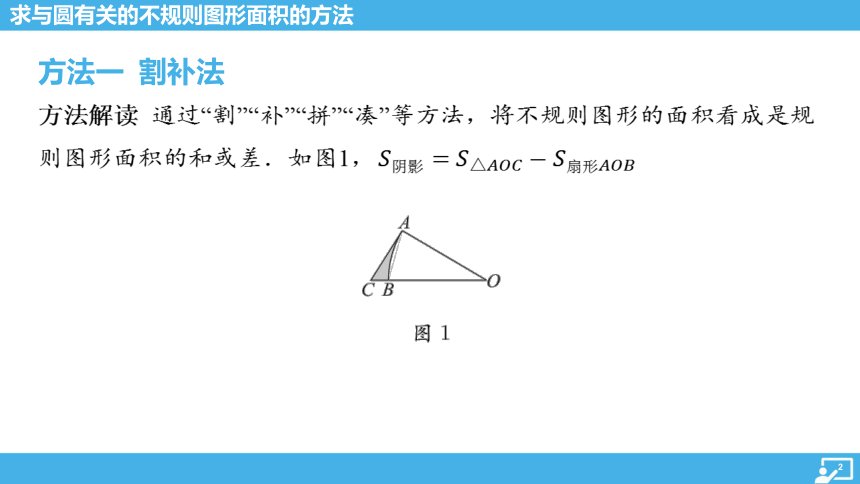
方法一 割补法
方法解读 通过“割”“补”“拼”“凑”等方法,将不规则图形的面积看成是规
则图形面积的和或差.如图1,
方法应用
图2
1.(2022·荆州)如图2,以边长为2的等边三角形
的顶点 为圆心,一定的长为半径画弧,恰好与 边
相切,且分别交 , 于点 , ,则图中阴影部分
的面积是( ) .
A. B. C. D.
图2
提示:设 边上的切点为 ,连接 ,则 .
在等边三角形 中, ,
, .在 中,
. .
【答案】D
图3
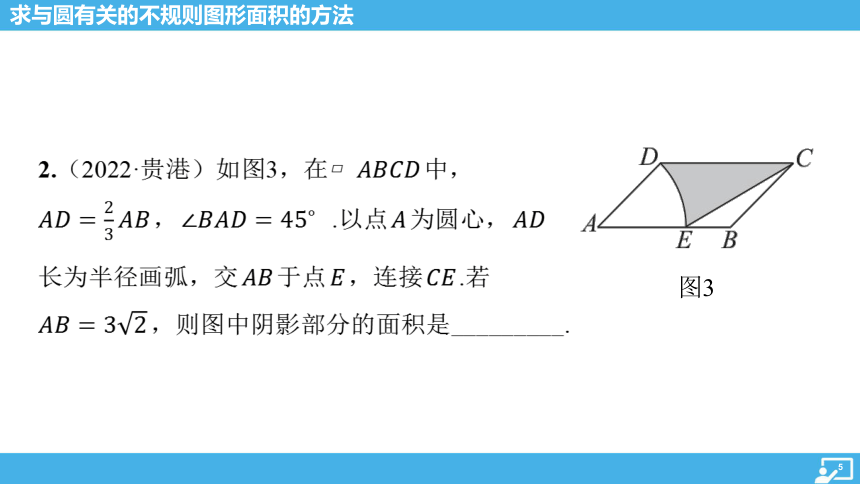
2.(2022·贵港)如图3,在 中,
, .以点 为圆心,
长为半径画弧,交 于点 ,连接 .若
,则图中阴影部分的面积是_________.
图3
提示:过点 作 于点 , , .又 ,
, . .
【答案】
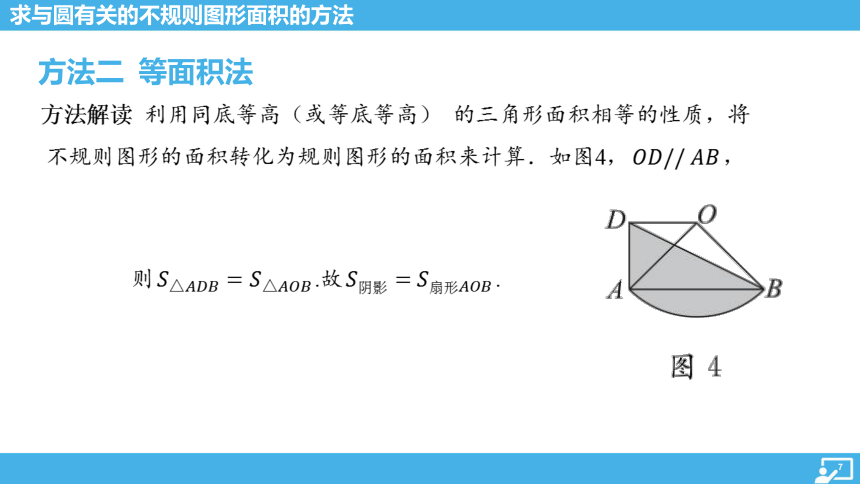
方法二 等面积法
方法解读 利用同底等高(或等底等高) 的三角形面积相等的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图4, ,
则 .故 .
方法应用
图5
3.(2023·广元)如图5,在半径为5的扇形 中,
, 是 上一点, , ,
垂足分别为点 , .若 ,则图中阴影部分的面
积为( ) .
B
A. B. C. D.
图6
4.如图6,点 , 是半圆 上的三等分点.若阴影
部分的面积为 ,则半圆 的半径 的长为___.
图55
提示:如图55,连接 , , .因为点 , 是
半圆 上的三等分点,所以
.又因为 ,所
以 为等边三角形,则 .所以
3
,则 .所以 .因此
,则 ,解得 (负值已舍去).
方法三 图形变换法
方法解读 利用图形在平移、旋转、对称变换前后面积不变的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图7, 绕点
旋转得到 ,则 .
方法应用
图8
5.如图8,网格图中每个小正方形的边长均为1,以
为半径的扇形 经过平移到达扇形 的位
置,那么图中阴影部分的面积是( ) .
B
A.8 B.6 C.6.5 D.7.5
图9
6.如图9,直径 长为6的半圆绕点 顺时针旋转 ,此
时点 旋转到点 处,则图中阴影部分的面积是( ) .
D
A. B. C. D.
方法四 整体法
图10
方法解读 当阴影部分图形由较多规则图形组成时,可以将
阴影部分图形视为一个整体来计算其面积.如图10, 与
的半径相同,两个小扇形的圆心角未知,则阴影部分
的面积可以转化为圆心角为 的扇形面积来计算.
方法应用
7.(2022·西宁)如图11,等边三角形 内接于 ,
,则图中阴影部分的面积是___.
图11
提示: 为等边三角形,且内接于 ,
, .过点 作 于点 .在 中, , ,
, , .
.
图12
8.(2023·重庆B卷)如图12,在矩形 中,
, , 为 的中点,连接 , .以点
为圆心, 长为半径画弧,分别与 , 交于点 ,
,则图中阴影部分的面积为______.
提示: , 为 的中点, .又 ,
.
.
微专题练习(十二)
求与圆有关的不规则图形面积的方法
方法一 割补法
图1
1.(2023·连云港)如图1,矩形 内接于 ,分别
以 , , , 为直径向外作半圆.若 ,
,则阴影部分的面积是( ) .
A. B. C. D.20
图91
提示:如图91,连接 ,则 过点 .在 中, , , 为直径的圆
为直径的圆 为直径的圆
.
【答案】D
图2
2.(2022·梧州)如图2,四边形 是 的内接正
四边形,分别以点 , 为圆心,取大于 的定长为
半径画弧,两弧相交于点 , ,作直线 ,交
于点 , .若 ,则 , , 所围成的阴影部
分的面积为_ __________.
图92
提示:如图92,连接 , .由题意可知,直线 垂
直平分线段 ,所以 .又因为 ,所以
为等边三角形.所以 .因为四边形
是 的内接正四边形,所以 .所以
.所以 .
【答案】
方法二 等面积法
图3
3.(2023·内蒙古)如图3,正方形 的边长为2,
对角线 , 相交于点 .以点 为圆心,对角线
的长为半径画弧,交 的延长线于点 ,则图中阴
影部分的面积为___.
图4
4.如图4,点 是半圆的圆心, 是半圆的直径,点
, 在半圆上,且 , ,
,则阴影部分的面积是____.
方法三 图形变换法
图5
5.(2022·铜仁)如图5,在边长为6的正方形 中,
以 为直径画半圆,则阴影部分的面积是( ) .
A
A.9 B.6 C.3 D.12
图6
6.(2022·河南)如图6,将扇形 沿 方向平移,
使点 移到 的中点 处,得到扇形 .若
, ,则阴影部分的面积为_ ______.
图93
提示:如图93,设 交 于点 ,连接 , ,又 ,
. , . ,
【答案】
.由平移变换知,
.
图7
7.(2022·黔西南)如图7,边长为4的正方形 的对
角线交于点 ,以 长为半径的扇形的圆心角
,则图中阴影部分的面积是_______.
图7
提示:因为四边形 是正方形,所以 ,
, ,
.因为
,所以 .在
和 中,因为 ,
, ,所以 .所以
.所以 .因为 是等腰直角三
角形, ,所以 .所以
.
【答案】
方法四 整体法
图8
8.教材变式[人教版九上第123页练习题7变式]如图
8, , , 的半径都是2,则阴影部分三个
扇形的面积之和是( ) .
A
A. B. C. D.
图9
9.(2021·重庆B卷)如图9,在菱形 中,对角
线 , ,分别以点 , , , 为
圆心, 长为半径画弧,与该菱形的边相交,则
图中阴影部分的面积为__________.
提示:在菱形 中,有 , ,所
以 .因为
,所以四
个扇形的面积和等于一个以 长为半径的圆.所以
.
【答案】
图9
求与圆有关的不规则图形面积的方法
方法一 割补法
方法解读 通过“割”“补”“拼”“凑”等方法,将不规则图形的面积看成是规
则图形面积的和或差.如图1,
方法应用
图2
1.(2022·荆州)如图2,以边长为2的等边三角形
的顶点 为圆心,一定的长为半径画弧,恰好与 边
相切,且分别交 , 于点 , ,则图中阴影部分
的面积是( ) .
A. B. C. D.
图2
提示:设 边上的切点为 ,连接 ,则 .
在等边三角形 中, ,
, .在 中,
. .
【答案】D
图3
2.(2022·贵港)如图3,在 中,
, .以点 为圆心,
长为半径画弧,交 于点 ,连接 .若
,则图中阴影部分的面积是_________.
图3
提示:过点 作 于点 , , .又 ,
, . .
【答案】
方法二 等面积法
方法解读 利用同底等高(或等底等高) 的三角形面积相等的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图4, ,
则 .故 .
方法应用
图5
3.(2023·广元)如图5,在半径为5的扇形 中,
, 是 上一点, , ,
垂足分别为点 , .若 ,则图中阴影部分的面
积为( ) .
B
A. B. C. D.
图6
4.如图6,点 , 是半圆 上的三等分点.若阴影
部分的面积为 ,则半圆 的半径 的长为___.
图55
提示:如图55,连接 , , .因为点 , 是
半圆 上的三等分点,所以
.又因为 ,所
以 为等边三角形,则 .所以
3
,则 .所以 .因此
,则 ,解得 (负值已舍去).
方法三 图形变换法
方法解读 利用图形在平移、旋转、对称变换前后面积不变的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图7, 绕点
旋转得到 ,则 .
方法应用
图8
5.如图8,网格图中每个小正方形的边长均为1,以
为半径的扇形 经过平移到达扇形 的位
置,那么图中阴影部分的面积是( ) .
B
A.8 B.6 C.6.5 D.7.5
图9
6.如图9,直径 长为6的半圆绕点 顺时针旋转 ,此
时点 旋转到点 处,则图中阴影部分的面积是( ) .
D
A. B. C. D.
方法四 整体法
图10
方法解读 当阴影部分图形由较多规则图形组成时,可以将
阴影部分图形视为一个整体来计算其面积.如图10, 与
的半径相同,两个小扇形的圆心角未知,则阴影部分
的面积可以转化为圆心角为 的扇形面积来计算.
方法应用
7.(2022·西宁)如图11,等边三角形 内接于 ,
,则图中阴影部分的面积是___.
图11
提示: 为等边三角形,且内接于 ,
, .过点 作 于点 .在 中, , ,
, , .
.
图12
8.(2023·重庆B卷)如图12,在矩形 中,
, , 为 的中点,连接 , .以点
为圆心, 长为半径画弧,分别与 , 交于点 ,
,则图中阴影部分的面积为______.
提示: , 为 的中点, .又 ,
.
.
微专题练习(十二)
求与圆有关的不规则图形面积的方法
方法一 割补法
图1
1.(2023·连云港)如图1,矩形 内接于 ,分别
以 , , , 为直径向外作半圆.若 ,
,则阴影部分的面积是( ) .
A. B. C. D.20
图91
提示:如图91,连接 ,则 过点 .在 中, , , 为直径的圆
为直径的圆 为直径的圆
.
【答案】D
图2
2.(2022·梧州)如图2,四边形 是 的内接正
四边形,分别以点 , 为圆心,取大于 的定长为
半径画弧,两弧相交于点 , ,作直线 ,交
于点 , .若 ,则 , , 所围成的阴影部
分的面积为_ __________.
图92
提示:如图92,连接 , .由题意可知,直线 垂
直平分线段 ,所以 .又因为 ,所以
为等边三角形.所以 .因为四边形
是 的内接正四边形,所以 .所以
.所以 .
【答案】
方法二 等面积法
图3
3.(2023·内蒙古)如图3,正方形 的边长为2,
对角线 , 相交于点 .以点 为圆心,对角线
的长为半径画弧,交 的延长线于点 ,则图中阴
影部分的面积为___.
图4
4.如图4,点 是半圆的圆心, 是半圆的直径,点
, 在半圆上,且 , ,
,则阴影部分的面积是____.
方法三 图形变换法
图5
5.(2022·铜仁)如图5,在边长为6的正方形 中,
以 为直径画半圆,则阴影部分的面积是( ) .
A
A.9 B.6 C.3 D.12
图6
6.(2022·河南)如图6,将扇形 沿 方向平移,
使点 移到 的中点 处,得到扇形 .若
, ,则阴影部分的面积为_ ______.
图93
提示:如图93,设 交 于点 ,连接 , ,又 ,
. , . ,
【答案】
.由平移变换知,
.
图7
7.(2022·黔西南)如图7,边长为4的正方形 的对
角线交于点 ,以 长为半径的扇形的圆心角
,则图中阴影部分的面积是_______.
图7
提示:因为四边形 是正方形,所以 ,
, ,
.因为
,所以 .在
和 中,因为 ,
, ,所以 .所以
.所以 .因为 是等腰直角三
角形, ,所以 .所以
.
【答案】
方法四 整体法
图8
8.教材变式[人教版九上第123页练习题7变式]如图
8, , , 的半径都是2,则阴影部分三个
扇形的面积之和是( ) .
A
A. B. C. D.
图9
9.(2021·重庆B卷)如图9,在菱形 中,对角
线 , ,分别以点 , , , 为
圆心, 长为半径画弧,与该菱形的边相交,则
图中阴影部分的面积为__________.
提示:在菱形 中,有 , ,所
以 .因为
,所以四
个扇形的面积和等于一个以 长为半径的圆.所以
.
【答案】
图9
同课章节目录
